Introduction

In the recent years, the challenge of removing heat from nanoelectronic devices1 and thermoelectrically converting waste heat into electricity has attracted huge scientific interest2, not only due to the questions posed for fundamental science, but also because thermoelectric energy conversion is an essential requirement for the next generation of nanoscale electronic, optoelectronic and photonic devices2. The efficiency of a thermoelectric device and material is determined by its thermoelectric figure of merit (ZT) defined as:

where S is the Seebeck coefficient (thermopower), G is the electrical conductance, T the temperature and κ the thermal conductance given by κ = κe + κp, where κe (κp) is the electronic (phononic) contribution to κ3. Clearly ZT could be enhanced by increasing the power factor (S2GT) or decreasing the thermal conductance and therefore a high-performance thermoelectric material should possess a large Seebeck coefficient and electrical conductance and simultaneously a low thermal conductance. The search for new materials with enhanced thermal properties continues to intensify, because these factors are correlated and increasing ZT to values greater than unity requires a delicate optimisation of several material properties.

One promising approach has been to reduce the contribution κp of parasitic phonons by nanostructuring materials4. Although acoustic phonons are the main heat carriers in bulk crystals, nanostructures can exhibit significantly lower phonon thermal conductances κp, due to increased phonon boundary scattering, changes in the phonon density of states and modified phonon dispersion in low-dimensional materials2. The nanostructuring of materials is also a promising route to increasing the power factor, because it can lead to sharp features in the electronic density of states and the transmission coefficient T(E) describing the propagation of electrons of energy E through a device. It is well known that the thermopower S is controlled by the asymmetry of T(E) at the Fermi energy EF and therefore if EF is close to such an asymmetry, both S and ZT will be enhanced. Unfortunately, asymmetries, even if they occur, are not necessarily located near EF and therefore a method of tuning them is required. In a nanoscale device, one could of course consider introducing a third gate electrode to control such features, but in practice this costs energy and does not solve the problem of designing a new material.

The above considerations suggest that an effective strategy for enhancing thermoelectric properties should 1) start from a parent material with low intrinsic thermal conductance, 2) nanostructure the material to further reduce the thermal conductance, 3) implement additional nanostructuring to introduce sharp features in T(E) and 4) chemically modify the material to move these sharp features towards the Fermi energy. In this paper our aim is to demonstrate that silicene, a new counterpart of graphene is an ideal material for implementing the four key elements of this strategy, because it is not only CMOS-compatible, but also it possesses a low intrinsic thermal conductance, which can be further reduced by nanostructuring the material to form nanoribbons.

Since silicon is the most common material used in the electronics industry, it is highly desirable to utilise silicon-compatible materials for thermoelectric energy conversion. Bulk silicon has a very low ZT (≈0.01) and therefore as a first step in a strategy for enhancing thermoelectric performance it is natural to focus on silicene, which is a recently-observed one-atom-thick crystalline form of silicon atoms arranged in a slightly buckled honeycomb lattice structure5,6,7,8,9,10,11,12. Silicene nanoribbons have been synthesised on silver (111)7,13,14,15,16,17,18,19,20,21,22,23,24,25, gold (110)26, iridium (111)27 and the zirconium diboride (0001)28,29 substrates and are predicted to be stable on non-metallic substrates30. Calculations of thermoelectric properties of armchair and zigzag silicene nanoribbons with and without hydrogen-passivated edges suggest that this material may be attractive for thermoelectric devices31,32,33,34, because the thermal conductivity of 2D silicene is predicted to be much smaller than bulk silicon and its counterpart graphene35, with only ~10% of the total phononic thermal conductivity being due to the out-of-plane acoustic phonons36,37. Both of these desirable features arise from the presence of small buckling, which breaks the reflection symmetry of the structure35,36. Further reductions in the phonon contribution arise from additional nanostructuring. For example the thermal conductivity of a silicene nanosheet 31,35,36,37 reduces to in zigzag silicene nanoribbons32,33,34. This could be potentially even lower in porous silicene, since the lattice thermal conductivity is reduced in nanoporous semiconductors38 such as nanoporous Bi39, Ge40, graphene41,42,43, Bi2Te344 and SiGe45. Moreover, it is been shown that placing nanopores in bulk silicon greatly reduces the thermal conductivity and enhances ZT by the factor of two46.

Since the low phonon thermal conductance of silicene is well established and therefore elements 1) and 2) of the above strategy are satisfied, in this paper we focus steps 3) and 4) and demonstrate that they can be achieved by inserting nanopores into silicene nanoribbons, whose edges are terminated by hydrogen or oxygen and by introducing adsorbates to tune the position of features in T(E) relative to EF. In view of the low value of κp, we will focus primarily on the electron contribution in thermoelectric figure of merit ZTe (obtained by setting κp = 0 in equation 1) and show that for ribbons containing nanopores with hydrogen-passivated edges, ZTe could be enhanced to values as high as 160 at room temperature by creating sharp features in the T(E) and controlling the Fermi energy or by introducing adsorbates such as Tetrathiafulvalene (TTF) and Tetracyanoquinodimethane (TCNQ) onto the silicene surface. We will then show that by including the κp of silicene nanoribbons, a high value of the full ZT of order 3.5 is achievable.

Results and Discussion

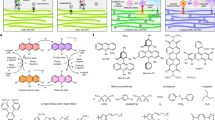
We have calculated the electronic contribution to the thermal conductance, the Seebeck and Peltier coefficients and ZTe for the structures shown in Figure 1c–h. The optimized lattice constant (a0) and buckling (d) of the silicene nanoribbon shown in Figure 1a are found to be 3.6 Å and 0.53 Å, respectively, similar to that reported elsewhere10,32,47. The engineered silicene nanoribbons shown in Figure 1 include: a zigzag monolayer silicene nanoribbon with hydrogen terminated edges (ZSiNR-H, Figure 1c), a zigzag monolayer silicene nanoribbon containing a nanopore with all edges terminated by hydrogen (ZSiNR-P, Figure 1d), a zigzag monolayer silicene nanoribbon with a central region containing oxygen terminated edges, connected to hydrogen-terminated leads (ZSiNR-HO, Figure 1e) and a zigzag monolayer silicene nanoribbon with oxygen terminated edges (ZSiNR-O, Figure 1f). The nanoribbons length and width in all cases are almost equal (L ≈ 6 nm (scattering region ≈ 3.48 nm), W ≈ 3 nm) and the pore diameter is ≈1.3 nm. We shall find that a key strategy for improving the thermoelectric performance of these structures involves tuning the Fermi energy (EF). As an example of how this could be achieved, we investigated the effect of introducing adsorbates onto the surface of the ZSiNR-P hydrogen-terminated nanoribbon, as shown in Figures 1f and 1g. The latter show examples of such functionalised ribbons containing adsorbed TTF (a strong electron donor) and TCNQ (a strong electron acceptor), which form charge-transfer complexes with the silicene.

Figure 1
figure 1

Sketch of the molecular structure of the Silicene and its alloys.

(a) silicene molecular structure, (b) a TTF (top) and TCNQ (bottom) doped silicene ribbon with two layers of dopant, (c) silicene monolayer ribbon with hydrogen terminated edges (ZSiNR-H), (d) silicene monolayer containing a nanopore (ZSiNR-P). All edges are terminated with hydrogen. (e) silicene monolayer ribbon with an oxygen terminated scattering region and hydrogen terminated electrodes (ZSiNR-HO), (f) silicene monolayer ribbon with oxygen terminated edges (ZSiNR-O), (g) as for (d), but with adsorbed Tetracyanoquinodimethane (TCNQ) and (h) as for (d), but with adsorbed Tetrathiafulvalene (TTF).

Full size image

Silicene nanoribbons and nanopores

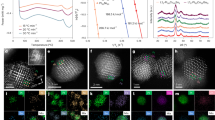
For the structures (c) to (f) of Figure 1, Figure 2 shows results for electrical conductance G, the electronic contribution of the thermal conductance κe, the thermopower S and the Peltier coefficient Π of the junction as a function of the temperature (T). All of these properties are obtained from the energy (E) dependence of the electron transmission coefficient T(E), shown in Figure 2a.

Figure 2
figure 2

Thermoelectric properties of the ZSiNR-H, ZSiNR-HO, ZSiNR-O and ZSiNR-P.

(a) Transmission coefficient T(E) (see Supplementary Information (SI) for a magnified version of this figure), (b, c) electrical and thermal conductance (G, κ), (d, e) Peltier (Π) and Seebeck (S) coefficients and (f) figure of merit (ZTe) as a function of temperature in the ZSiNR-H, ZSiNR-HO, ZSiNR-O and ZSiNR-P.

Full size image

Figure 2 shows that the silicene nanoribbons ZSiNR-H, ZSiNR-HO and ZSiNR-O possess high electronic thermal conductances and low thermopowers and consequently their figures of merit (ZTe) are low. However, the results for the silicene monolayer nanoribbon containing a nanopore (ZSiNR-P) show that ZTe is significantly improved by placing a hole in the ribbon. This arises because the densities of states of all four structures possess sharp peaks around the Fermi energy EF due to band bending in the corner of the k-space in silicene band structure, which introduces a sharp feature (indicated by an arrow in Figure 2a) in T(E) near EF. Furthermore the T(E) of ZSiNR-P possess the desirable feature that T(E) is almost zero on either side of the peak. This feature is associated with edges states, which is why it is sensitive to the chemical nature of the edge terminations. These edge states are a well-known feature of nanoribbons with zigzag edges48,49,50 and lead to a significant improvement in the thermopower (Figure 2e) as well as a reduction in the thermal conductance (Figure 2d). Edge states have been predicted earlier theoretically51 and observed experimentally52,53,54 in graphene nanoribbons. By comparing ZSiNR-P with ZSiNR-H or by comparing ZSiNR-HO with either ZSiNR-P or ZSiNR-O, Figure 2 demonstrates the general trend that introducing scattering reduces both the electrical and thermal conductances and simultaneously increases the thermopower. Figure 2 also reveals the attractive property that ZSiNR-P possesses the highest room-temperature ZTe (of order 1.4) and that this high thermoelectric efficiency is preserved over a wide range of temperature from 100 K to 500 K.

To highlight the role of sharp features near EF in the transmission coefficients of Figure 2a, we investigate a simple model for which T(E) = a + b for and T(E) = a for EF outside this range. As shown in Figure 3a, possesses a rectangular peak of height b, width σ, located at an energy E0 relative to the Fermi energy EF = 0 eV. The peak is superposed on a constant background of height a. Crudely, on the scale of kBT and for relevant values of E0, the transmission coefficient of ZSiNR-P corresponds to the case b = 1, a = 0, ZSiNR-O corresponds to a = b = 5 (ie no peak), whereas ZSiNR-H corresponds to a = 1, b = 3.

Figure 3
figure 3

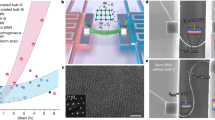
Thermoelectric properties of a system with Delta function like transmission coefficient T(E).

(a) Delta transmission coefficient with the width of σ and mean of E0 and a = 0 and b = 1 and corresponding (b) conductance (G/G0), (c) electronic thermal conductance (κe), (d) Seebeck coefficient (S), (e) logarithm of electronic ZT (log10(ZTe)) and (f) total ZT (with phononic and electronic contribution) as a function of σ and E0 in the room temperature. E0 represents the position of the peak in the transmission function relative to the Fermi energy EF = 0.

Full size image

For the case of ZSiNR-P, where b = 1, a = 0, Figures 3b–e show the conductance (G/G0), electronic thermal conductance (κe), Seebeck coefficient (S) and the logarithm of electronic figure of merit (ZTe) as a function of σ and E0 at room temperature. As shown in Figure 3e (right hand side of horizontal dashed line), ZTe could increase up to 106 provided the width σ is sufficiently small. However, for a broad transmission peak close to Fermi energy one obtains a very low electronic thermoelectric figure of merit down to ~10−5 (left hand side of dashed line). This is mainly due to reduction of electronic thermal conductance (Figure 3c), because the thermopower decreases more slowly (Figure 3d) than the electronic thermal conductance.

The above simple model and the results of Figure 2 demonstrate that the thermoelectric performance of silicene nanoribbons is improved by the introduction of nanopores. To demonstrate that further dramatic improvements are available if the Fermi energy is tuned by an external gate, figure 4 shows results for ZTe, S and κe as a function of EF, obtained from the exact transmission curves T(E) of Figure 1a. This demonstrates that at room temperature, the electronic contribution to ZTe can be hugely enhanced by varying the Fermi energy by as little as 100 meV, with achievable values as high as 160. Furthermore the sign of the thermopower can be selected by such tuning, with achievable values as high as S = +/− 500 μV/K.

Figure 4
figure 4

Room temperature thermal properties of the ZSiNR-H, ZSiNR-HO, ZSiNR-O and ZSiNR-P in different Fermi energies EF.

(a) The variation of room-temperature values of ZTe, (inset is ZTe on the logarithmic scale), (b) electronic thermal conductance κe and (c) Seebeck coefficient S as a function of EF for ZSiNR-H, ZSiNR-HO, ZSiNR-O and ZSiNR-P. The main part of fig. 4a shows ZTe for ZSiNR-P on a linear scale.

Full size image

This improvement could be achieved by electrostatically-gating the nanopore-containing ribbon. For the purpose of improving intrinsic material performance, we demonstrate below that a Fermi energy shift can also be realised by introducing donor or acceptors onto the surface of the silicene nanoribbon. However before considering the effect of doping, we examine the effect of phonons, since ZTe is obtained by neglecting the phononic contribution (κp) to the thermal conductance in equation (1). This is a reasonable approximation to the full figure of merit ZT provided the electronic thermal conductance (κe) is higher than phononic thermal conductance. However large values of ZTe correspond to the opposite limit of low values of κe, where κp > κe. In this limit, one needs to consider only the phononic contribution and consequently the denominator of equation (1) becomes a constant, independent of σ and E0.

To estimate the κp for the structure of figure 1d, we note that for a perfect zigzag silicene nanoribbon of width equal to the bridging sections of silicene above and below the pore of Figure 1d is predicted to have a phononic thermal conductance κp of less than 6 × 10−11 W/K32. This value contrasts markedly with graphene, whose thermal conductance is predicted to be a factor of at least 50 times higher36. As discussed in the introduction, boundary scattering by nanopores can lead to a further order of magnitude reduction in κp and therefore a value of κp on the scale of ~10−12 W/K would seem reasonable for the structure of Figure 1d. For the model T(E) of Figure 3a, Figure 3f shows the full ZT when the thermal conductance is dominated by phonons, with a high thermal conductance of κp = 2 × 10−11 W/K. This demonstrates that even in the most unfavourable scenario, the full ZT could achieve a value as high as 3.5 for values of σ and E0 lying in the red region of Figure 4f (where σ ~ 2E0 − 0.1). The transmission coefficient of the silicene nanopore (ZSiNR-P) shown in Figure 2a could be approximately modelled by b = 1, a = 0 with the width of σ = 0.025 and a mean of E0 = 0.015 around the Fermi energy. The crossover of dotted lines in Figure 3e shows the model ZTe at room temperature, which is in good agreement with the value of ZTe obtained from the more accurate T(E) shown in Figure 2f. By increasing E0, Figure 3f suggests that values of the full figure of merit as high as ZT = 3.5 are possible. On the other hand (see SI) for the ZSiNR-O (a = b = 5) and ZSiNR-H (a = 1, b = 3), the presence of a non-zero background suppresses the achievable values of ZT. For this reason, we now focus on tuning the properties of the H-terminated nanopore and demonstrate that high values of ZTe can be achieved by doping the surface of the silicene.

Adsorbate-functionalized silicene

For the purpose of improving intrinsic material performance, a method of shifting EF by doping the silicene nanoribbon is needed. Since covalent bonding of dopants to the nanoribbons may adversely affect electronic properties, we now consider tuning the Fermi energy by adsorbing planar molecules which interact with the surface only through weak pi-pi interactions. The first adsorbed molecule we study is Tetrathiafulvalene (TTF) which is a strong donor and the second is Tetracyanoquinodimethane (TCNQ), which is a strong acceptor55.

In the presence of adsorbates, calculations were performed by relaxing the adsorbates to find their minimum-energy states on the surface of the silicene (see methods), which yielded an optimized distance between the silicene and TCNQ of 3.1 Å and 3.54 Å for TTF. For the lowest dopant concentrations, we place a monolayer or sub-monolayer of TTF or TCNQ on the surface of the electrodes of ZSiNR-P, as shown in Figures 1g and 1h, whereas for the highest concentration, two layers above and below the silicene are included, as shown in Figure 1b. Figure 5 shows that TTF on silicene simultaneously increases the Seebeck coefficient, decreases the thermal conductance and increases ZTe from an undoped value of 1.4 to 1.7, 1.85 and 3.1 with increasing concentration from 21% to 43% and 87%, where the concentration of adsorbate is defined as the ratio of the number of TTF atoms to the number of silicene nanoribbon atoms. The inset of Figure 6 shows the variation of ZTe with EF for different concentrations of TTF and reveals that an 87% coverage produces a Fermi energy shift of approximately 3 meV. The transmission just around the Fermi energy is shown in Figure S2b of SI.

Figure 5
figure 5

Thermoelectric properties of the intrinsic and doped ZSiNR-P with various dopant and concentrations.

(a) Transmission coefficient T(E) (see SI for a magnified version of this figure), (b, c) electrical and thermal conductance (G, κ), (d, e) Peltier (Π) and Seebeck (S) coefficients and (f) figure of merit as a function of temperature. Results are shown for a monolayer silicene nanopore (ZSiNR-P) with a perfect zigzag silicene ribbon electrodes, a monolayer silicene nanopore with TCNQ functionalized zigzag silicene nanoribbon electrodes with low concentration of TCNQ (ZSiNRP-TCNQ) and with higher concentration of TCNQ (ZSiNRP-2×TCNQ), a monolayer silicene nanopore with TTF functionalized zigzag silicene ribbon electrodes with low concentration of TTF (ZSiNRP-TTF) and with higher concentrations of TTF (ZSiNRP-2×TTF and ZSiNRP-4×TTF).

Full size image
Figure 6
figure 6

The effect of the dopant on the thermoelectric figure of merit.

Thermoelectric figure of merit (ZTe) in EF = 0 for ZSiNR-P doped with 0%, 21%, 43% and 87% TTF in T = 250 K, 300 K and 350 K. inset: The variation of room-temperature (T = 300 K) values of ZTe as a function of EF in intrinsic and doped ZSiNR-P with 21% TTF (ZSiNRP-TTF), with 43% TTF (ZSiNRP-2×TTF) and with 87% TTF (ZSiNRP-4×TTF).

Full size image

In summary, we have developed a new strategy for improving the thermoelectric performance of silicene-based nanoribbons by investigating the effect of introducing nanopores and varying their edge termination. We have demonstrated that the thermopower and electronic thermoelectric figure of merit ZTe can be improved by introducing nanopores and tuning their Fermi energy. By shifting the Fermi energy by approximately 100 meV from the charge-neutrality point, we predict that huge values of ZTe up to 160 are accessible and that the sign of the thermopower can be varied with achievable values as high as S = +/− 500 μV/K. As a method of tuning the Fermi energy, we analysed the effect of doping the silicene with either a strong electron donor (TTF) or a strong electron acceptor (TCNQ) and demonstrated that doping by the former tended to decrease the value of ZTe, because the Fermi energy shift was in an unfavourable direction. On the other hand, we found that doping with TTF increased the room-temperature value to ZTe to 3.1 and that this value is insensitive to temperature over the range 100 K – 400 K. This combination of a high temperature-insensitive ZTe and the fact that the low phonon thermal conductance renders ZTe comparable with the full figure of merit ZT, identifies nanoporous silicene as an ideal thermoelectric material with the potential for unprecedented performance.

Methods

To find the optimized geometry and ground state Hamiltonian of the structures of interest, we employed the SIESTA56 implementation of Density Functional Theory (DFT) using the generalized gradient approximation (GGA) of the exchange and correlation functional with the Perdew-Burke-Ernzerhof parameterization (PBE)57 a double zeta polarized basis set, a real-space grid defined with a plane wave cut-off energy of 250 Ry and a maximum force tolerance of 40 meV/Ang. The calculation with VDW-DF exchange and correlation functional with BH parameterization was also carried out to check the GGA-PBE result in some cases. The BH is the same as DRSLL with some modification58. From the converged DFT calculation, the underlying mean-field Hamiltonian was combined with our transport code, GOLLUM59 which is an implementation of the non-equilibrium Green's function (NEGF) method. This yields the transmission coefficient T(E) for electrons of energy E (passing from the source to the drain) via the relation

In this expression, ΓL,R(E) = i (ΣL,R(E) − ΣL,R†(E)) describes the level broadening due to the coupling between left (L) and right (R) electrodes and the central scattering region, ΣL,R(E) are the retarded self-energies associated with this coupling and GR = (ES − H −ΣL − ΣR)−1 is the retarded Green's function, where H is the Hamiltonian and S is overlap matrix (both of them obtained from SIESTA). Thermal properties such as the electrical conductance G(T), the electronic contribution of the thermal conductance κe(T), the thermo-power S(T) and the Peltier coefficient Π(T) of the junction as a function of the temperature are given by59:

where

and T(E) is the transmission coefficient, f(E) is the Fermi-Dirac probability distribution function (f(E) = (1 + exp (E − EF/kBT))−1), T is the temperature, EF is the Fermi energy, G0 = 2e2/h is the conductance quantum, e is electron charge and h is the Planck's constant. From these expressions, the electronic contribution to the figure of merit ZTe is: