Abstract
Transformation optics is a powerful tool to design various novel devices, such as invisibility cloak. Fantastic effects from this technique are usually accompanied with singular mappings, resulting in challenging implementations and narrow bands of working frequencies. Here in this article, Fabry-Pérot resonances in materials of extreme anisotropy are used to design various transformation optical devices that are not only easy to realize but also work well for a set of resonant frequencies (multiple frequencies). As an example, a prototype of a cylindrical concentrator is fabricated for microwaves.
Similar content being viewed by others
Introduction
Transformation optics1,2 has become a juicy topic since it emerged in 2006, as a fantastic tool to design various devices with novel functionalities. Readers can find the progress in a recent review3. One of the key concerns however in this field is that, the devices designed for the intriguing effect usually come from some singular mappings. The singular material parameters are thereby required, regardless the difficulty in fabrication. Even if we can acquire some of them, the work spectra are mostly in a very narrow band4. By sacrificing the material parameters (therefore some of the functionalities) for non-singular cases, broadband devices are proposed and realized (e.g., the carpet cloak5,6,7,8,9,10). Therefore, we see that these two factors, fancy effect and broadband functionality, are competing against each other, bringing about quite a dilemma for the field to advance.
In this article, we will prove that Fabry-Pérot (FP) resonances can address this difficulty to some extent. Firstly, we will propose a simple one dimensional singular mapping, which can be used to design a device called "optical void". We then set equivalency between such an optical void with the one dimensional metallic slit array. The working frequencies are right at the FP resonances. With this, we can design various devices, such as a concentrator, a shifter, a rotator, a waveguide bend and a waveguide periscope. In particular, we fabricate a prototype of a concentrator for microwave frequencies. Our approach can be used to design novel devices for a series of frequencies. However, the functionalities will be compromised if the working frequencies deviate too much from the FP resonant frequencies.
Methods
Theory and simulation
All the simulated field patterns and the scattering cross sections in Figure 6 are obtained using the finite element solver COMSOL Multiphysics.
The concentrator and the effect.
(a) The photo of the concentrator with the solid Plexiglas cylinder; (b) The measured Hz field immediately neighboring the concentrator at 9.26 GHz; (c) The simulated result; (d) The photo of the bare Plexiglas cylinder; (e) The measured Hz field immediately neighboring the cylinder at 9.26 GHz; (f), The simulated result.
Sample fabrication
The field concentrator is a cylindrical object comprising thin iron sheets arranged into the theoretically designed pattern. The iron sheet has the thickness 0.3 mm and is cut into the 32 × 500 mm2 rectangular piece. We fabricated the total 100 pieces and assembled them to be the concentrator. Their relative positions were fixed via inserting the iron pieces into an annular Plexiglas slice with designed radial slits. By using several Plexiglas slice fixtures, we fabricated the field concentrator which has an annular cross section of 50 mm < r′ < 82 mm and a height of 500 mm. To facilitate the measurement, the second concentrator with 72 iron pieces and the size 50 mm < r′ < 80 mm is made to be used together with the oil cylinder.
Experimental set-up
In the experiment, the samples are placed vertically with the cylindrical axis orientated along the z-direction and a horn-shaped antenna, located ~100 cm away from the field concentrator, transmits microwaves toward the sample with the H-field polarized along the vertical direction, as depicted in Supplementary Fig. S1. To map the spatial distribution of the Hz component, we employ a split ring detecting antenna which is made of a coaxial cable and has a circular loop of diameter 4 mm and a split 1 mm. Its S11 spectrum is measured and shown in Supplementary Fig. S2, displaying a magnetic radiating/receiving characteristic around 10 GHz. To detect the magnetic field inside the oil sample, the ring plane of the detector is perpendicular to the z-directed coaxial cable which is inserted into the oil from the top of the sample. The split-ring antenna as well as the coaxial cable is mounted on a two-dimensional translation stage and is controlled to move in the horizontal x-y plane. The scanning range covers a square of 300 × 300 mm2 with a spatial resolution of 2 × 2 mm2, but the central area is not accessible due to the sample occupation, as marked by the dashed lines in Supplementary Fig. S1. The horn antenna and the detector are connected to an S-parameter network analyzer to obtain the magnitude and phase of the Hz field.
Measurements
Before the measuring the field patterns of the scatters or concentrators, we scan the magnitude and phase of the incident Hz field in air at 9.26 GHz in Supplementary Fig. S3(a) and (b). Supplementary Fig. S3(c) shows the real part of Hz field, which has the quasi-plane wave feature with slightly curved wavefronts. The related simulated magnitude, phase and the real part of the incident Hz field are shown in Supplementary Fig. S3(d), (e) and (f). Likewise, Supplementary Fig. S4(a), (b) and (c) show the magnitude, phase and the real part of incident Hz field in air at 9.35 GHz, while the related simulated magnitude, phase and the real part are shown in Supplementary Fig. S4(d), (e) and (f). To get the field pattern of the bare solid Plexiglas cylinder in Fig. 5e (or Supplementary Fig. S5(c)), we scan the magnitude and phase of the Hz field in Supplementary Fig. S5(a) and (b). The simulated magnitude, phase and the real part of the Hz field are shown in Supplementary Fig. S5(d), (e) and (f). Likewise, we measure the magnitude and phase of the Hz field for the concentrator with the solid Plexiglas cylinder in Supplementary Fig. S6(a) and (b), which can be used to obtain the real part of the Hz field in Supplementary Fig. S6(c) (or Fig. 5c). The simulated magnitude, phase and the real part of the Hz field for the concentrator are shown in Supplementary Fig. S6(d), (e) and (f). For the bare oil cylinder, the magnitude, phase and the real part of the Hz field are shown in Supplementary Fig. S7(a), (b) and (c) (or Fig. 7e), while the simulated magnitude, phase and the real part are shown in Supplementary Fig. S7(d), (e) and (f). For the concentrator with the oil cylinder, the magnitude, phase and the real part of the Hz field are shown in Supplementary Fig. S8(a), (b) and (c) (or Fig. 7c), while the simulated magnitude, phase and the real part are shown in Supplementary Fig. S8(d), (e) and (f).
The concentrator with oil cylinder and the effect.
(a) The photo of the concentrator with the oil cylinder; (b) The measured Hz field immediately neighboring the concentrator and inside the oil at 9.35 GHz; (c) The simulated result; (d) The photo of the bare oil cylinder; (e) The measured Hz field immediately neighboring the cylinder and inside the oil at 9.35 GHz; (f), The simulated result.
Results and Discussion
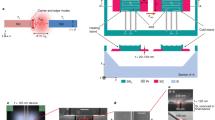
Let us start with the simple mapping (see in Fig. 1c):

This mapping transformed a slab x1 ≤ x < x2 in virtual space (Fig. 1a) into a slab x1′ ≤ x < x2′ in physical space (Fig. 1b). Suppose the virtual space is free space, we can obtain the material tensors of the slab x1′ ≤ x < x2′,

where  . If x2 → x1, Δ → ∞, the slab x1′ ≤ x < x2′ functions as an optical void, which means that when wave impinges, the phase does not accumulate after passing through it.
. If x2 → x1, Δ → ∞, the slab x1′ ≤ x < x2′ functions as an optical void, which means that when wave impinges, the phase does not accumulate after passing through it.
As an example, we plot the field pattern for a point source setting nearby the optical void in Fig. 2a and choose the transverse magnetic (TM) polarization in this article, as we will later see that such a polarization with FP resonances has an advantage over the transverse electric (TE) polarization. Notice that all the calculations in this article are performed by the commercial FEM software COMSOL. Here only εx = Δ and εy = μz = 1/Δ are required. In the simulation, we set Δ = 100000, x2′ − x1′ = 2 and the wavelength λ = 1. The point source is a numerical test by setting the magnetic field Hz as a constant at a tiny circular boundary. From the field pattern, we find that the image of the point source is perfectly transmitted from left to right, indicating the functionality of the optical void.
Now we recall the one dimensional metallic slit array, which can support spoof surface plasmons11. Suppose the slit array is along x-direction, the width of the slits is a, the width of the unit cell along y-direction is d, as shown in Fig. 2b. Through the design of the perfect endoscopes (materials with extreme anisotropy)12,13,14,15,16,17,18,19,20,21,22,23, we know that when x2′ − x1′ = mλ (m = 1,2,3…), the same functionality of the optical void can be achieved. For example, as we set d = 2a = 0.1 in Fig. 2c, the slit array can perfectly transmit an image of a point source at λ = 1 (here m = 2). As λ ≫ d, the slit array can also be regarded as a slab with εx = ∞, εy = 2 and μz = 0.511. The same functionality of this effective medium is demonstrated in Fig. 2d (in the simulation εx = 100000). In fact, we numerically find a general condition for such a perfect transmission from full-wave simulations, i.e.,

the optical path in x-direction is integer times of the wavelength, which is actually the FP resonance condition (for simple cases, such as a homogeneous slab, this condition can be analytically proved following Ref. 18). For TE modes, the thin slits cannot transmit waves as the working frequencies are below the cut-off frequencies.
After the above equivalency is built up between the optical void and the metallic slit array, we can use the FP resonances in transformation optics and design many devices that can be easily implemented and capable of working for a series of frequencies. To the best of our knowledge, this is the first time that FP resonances in materials of extreme anisotropy are used to design transformation media.
For example, let us look at a similar mapping in circular cylindrical coordinate (see in Fig. 3c)24,

which maps a concentric cylindrical layer r1 ≤ r < r2 in virtual space (Fig. 3a) into another concentric cylindrical layer r1′ ≤ r′ < r2′ in physical space (Fig. 3b). This is a mapping to design a concentrator if we set virtual space as free space, r2′ = r2 and r1′ < r1. If r1 → r2, we shall have εr → ∞, εθ → 0 and μz → 0 for r1′ ≤ r′ < r2′ and ε = 1 and  for 0 ≤ r′ < r1′. Figure 4a shows the perfect transparency of such a concentrator for λ = 1, where we set r2′ = r2 = 2, r1′ = 1 and r1 = 1.9999.
for 0 ≤ r′ < r1′. Figure 4a shows the perfect transparency of such a concentrator for λ = 1, where we set r2′ = r2 = 2, r1′ = 1 and r1 = 1.9999.
Inspired by the above FP resonance in x-direction, here we can also design a concentrator from FP resonance in r-direction. For example, we can set εr = ∞, εθ = εθ(r′) and μz = 1 for r1′ ≤ r′ < r2′ and  and μz = 1 for 0 ≤ r′ < r1′. The FP resonance condition in r-direction is now numerically found as:
and μz = 1 for 0 ≤ r′ < r1′. The FP resonance condition in r-direction is now numerically found as:

The factor 2 comes up as the waves pass the concentrator twice in r-direction, which is consistent with Eq. (3). Such a concentrator does not have any magnetic response and can work for a series of frequencies. To show the similar perfect transparency, we plot the field pattern in Fig. 4b for εθ(r′) = (3 − r′)2 and λ = 1 (here m = 3, r2′ = 2, r1′ = 1). We note that such a version is a perfect one as the impedances match at both boundaries (r′ = r1′ and r′ = r2′). Different from the conventional concentrator (where the core medium shares the same magnetic field amplitude with the background medium), the magnetic field amplitude here is twice (in general,  ) as big as that of the background medium. However, the total energy of the core medium in both cases is the same, i.e., four times (in general,
) as big as that of the background medium. However, the total energy of the core medium in both cases is the same, i.e., four times (in general,  ) of the incident energy (a conclusion from the numerical simulations).
) of the incident energy (a conclusion from the numerical simulations).
How can we realize such a concentrator? We can simply insert thin metallic plates along r-direction in a dielectric profile ε(r′) in r1′ ≤ r′ < r2′, see the schematic plot in Fig. 4c. For example, we insert 144 pieces of metallic plates and plot the field pattern for λ = 1 in Fig. 4d, where almost perfect transparency can be observed. The effect medium in r1′ ≤ r′ < r2′ should be modified to εr = ∞, εθ = ε(r′)/(1 − f) and μz = 1 − f (f is the filling ratio of the inserted metallic plates). In this simulation, f = 0.2. If f is too large, impedances will mismatch at both boundaries (r′ = r1′ and r′ = r2′), causing some scattering and imperfection. We note that a similar configuration of radially arranged plates (superconducting materials plus soft ferromagnetic materials) has been proposed as a concentrator for static magnetic fields25. However, our work here is the first experimental attempt to realize a concentrator at finite frequencies, hence it is a breakthrough when comparing to the theoretical explorations24,25.
Now we come to implement a reduced version of the above Fig. 4c. As it is still quite tedious to realize the part between r1′ ≤ r′ < r2′. We make further reduction, that is, to just insert the metallic plates in air. We find from simulation that, apart from a little scattering induced by the impedance mismatching at the inner boundary r′ = r1′, the concentrating effect is still there. To get a perfect transparency like that in Fig. 4c, we can simply replace the dielectric core ( and μz = 1) with a metamaterial core (
and μz = 1) with a metamaterial core ( ). We prove such a perfect transparency analytically in Supplementary Note S1. The device can work almost perfectly for a series of FP resonant frequencies, each with a very narrow bandwidth.
). We prove such a perfect transparency analytically in Supplementary Note S1. The device can work almost perfectly for a series of FP resonant frequencies, each with a very narrow bandwidth.
The concentrator is assembled using the thin iron pieces, with an annular cross section of 50 mm < r′ < 82 mm in its final form and is fixed surrounding a solid Plexiglas cylinder with a dielectric constant 2.7 (see in Fig. 5a). Fig. 5b is the measured Hz field at 9.26 GHz. The scanning range measures 300 × 300 mm2, starting with the upper left corner and the quasi-plane wave with slightly curved wavefronts is incident towards the -y-direction. The central area in the scanning region is not accessible due to the sample occupation. It is seen that the wave recovers its original wavefronts with negligible intensity decay after passing through the sample, which points out the scattering free feature of our device. To show the full picture of the Hz field, we show the simulation result in Fig. 5c, where the concentrating effect is well demonstrated with a little scattering. For comparison, we also present the results for the bare Plexiglas cylinder (photo taken in Fig. 5d). The measured Hz field at 9.26 GHz is shown in Fig. 5e and the related simulated result is shown in Fig. 5f, where we find that the scattering is enlarged. From the simulation, the dielectric core also shows a focusing effect. But with the concentrator, the wavefronts inside it become quite flat, as shown in Fig. 5c.
In fact, from the simulation, we find that the best working frequency is at 9.5 GHz. But due to the imperfection of the sample fabrication, the working frequency is shifted to 9.26 GHz. In Fig. 6, we plot the frequency dependences of the total scattering cross sections for the bare dielectric core and the concentrator with metallic plates. We find that the concentrator here works well for multiple frequencies. Near the resonant frequencies, the scattering cross sections are smaller than those of the bare dielectric core due to FP resonance in r-direction. Although the scattering at each FP resonant frequency turns bigger when compared to the perfect one in Supplementary Note S1 (due to the impedance mismatching at the inner boundary between air and dielectrics), the device here works for a broader band of frequencies.
In order to detect the field inside the core region in the concentrator, we employed a liquid sample, as illustrated in Fig. 7a. A cylindrical Plexiglas container with the inner radius 45 mm, the outer radius 50 mm and the height 53 cm is filled with castor oil, as shown in Fig. 7d. Because the castor oil has the dielectric constant 2.6 + 0.1i, close to the Plexiglas's value 2.7, the oil loaded container is considered to be a liquid cylinder. The associated concentrator is fabricated using 72 iron pieces and has an annular cross section of 50 mm < r′ < 80 mm in its final form. Besides scanning the exterior field, we insert the detector into the oil to sense the interior field inside the oil cylinder. A central square in the cylindrical container is now accessible to our detector. Figure 7b and 7c are the measured and simulated Hz field at 9.35 GHz, respectively. The field patterns show that the scattering is small and the wavefronts in the oil are flat, which turns out to coincide with the concentrating effect as predicted. For comparison, we also present the results for the bare oil cylinder in Fig. 7d. The measured Hz field and the simulated result at 9.35 GHz are shown in Fig. 7e and 7f, respectively. From the measured field pattern in the oil cylinder, the focusing effect is seen clearly and is consistent with the simulated result. Due to the imperfection of the sample fabrication and the dissipation in the oil core, the working frequency is now shifted from 10 GHz to 9.35 GHz.
Apart from the above implementation of a reduced FP concentrator, we also design a shifter26, a rotator27, a waveguide bend28 and a waveguide periscope in the Supplementary Figures. In general, to apply FP resonances in transformation optics, optical voids should be designed first. Given the same principle as the above, we only numerically show the refractive index profiles and the related functionalities. Supplementary Fig. S9(a) shows the index profile of the shifter, which is composed of oblique metallic slit arrays. Supplementary Fig. S9(b) shows that the beam incident to the shifter has a displacement in y-direction after passing through it. By inserting specially designed curved metallic structures into an index profile in Supplementary Fig. S10(a), a perfect rotator can be implemented and the functionality is shown in Supplementary Fig. S10(b). Thirdly, we can implement devices by combining the optical conformal mapping1,29 together with the FP resonances. As the optical conformal mapping (from z = x + iy to w = u + iv) keeps the optical paths unchanged, i.e.,  , if we insert curved metallic structures along u-lines (or v-lines), the phase changes of any waves at v-lines (or u-lines) will be unchanged, therefore all the paths have the same FP resonant frequencies. Take w = 2 ln z as an example, we can design a waveguide bend. The index profile is shown in Supplementary Fig. S11(a) (with the metallic structures along the θ-direction), while the related functionality is proved in Supplementary Fig. S11(b). Likewise, if we use the Zhukowski mapping, i.e., w = z + 1/z, a perfect one dimensional cloak can be achieved (not shown in this article). Finally, we show a perfect waveguide periscope in Supplementary Fig. S12 (a) by simply inserting a specially designed curved metallic structure in air. The functionality is demonstrated in Supplementary Fig. S12 (b). In fact, the concentrator here can also be used as a hyperlens30, or even find some potential application in energy harvests or wireless power transfer.
, if we insert curved metallic structures along u-lines (or v-lines), the phase changes of any waves at v-lines (or u-lines) will be unchanged, therefore all the paths have the same FP resonant frequencies. Take w = 2 ln z as an example, we can design a waveguide bend. The index profile is shown in Supplementary Fig. S11(a) (with the metallic structures along the θ-direction), while the related functionality is proved in Supplementary Fig. S11(b). Likewise, if we use the Zhukowski mapping, i.e., w = z + 1/z, a perfect one dimensional cloak can be achieved (not shown in this article). Finally, we show a perfect waveguide periscope in Supplementary Fig. S12 (a) by simply inserting a specially designed curved metallic structure in air. The functionality is demonstrated in Supplementary Fig. S12 (b). In fact, the concentrator here can also be used as a hyperlens30, or even find some potential application in energy harvests or wireless power transfer.
Conclusions
In conclusion, we have shown that FP resonances can help to design various transformation optical devices, which can not only be easily implemented as they are only composed of (curved if necessary) metallic structures and dielectric profile, but can also work for a series of frequencies. As an example, we fabricate a prototype for a concentrator in microwaves and demonstrate its functionalities.
References
Leonhardt, U. Optical conformal mapping. Science 312, 1777–1780 (2006).
Pendry, J. B., Schurig, D. & Smith, D. R. Controlling electromagnetic fields. Science 312, 1780–1782 (2006).
Chen, H., Chan, C. T. & Sheng, P. Transformation optics and metamaterials. Nat Mater 9, 387–396 (2010).
Schurig, D., Mock, J. J., Justice, B. J., Cummer, S. A. & Pendry, J. B. et al. Metamaterial electromagnetic cloak at microwave frequencies. Science 314, 977–980 (2006).
Li, J. & Pendry, J. B. Hiding under the carpet: A new strategy for cloaking. Phys Rev Lett 101, 203901 (2008).
Liu, R., Ji, C., Mock, J. J., Chin, J. Y. & Cui, T. J. Broadband ground-plane cloak. Science 323, 366–369 (2009).
Valentine, J., Li, J. S., Zentgraf, T., Bartal, G. & Zhang, X. An optical cloak made of dielectrics. Nat Mater 8, 568–571 (2009).
Gabrielli, L. H., Cardenas, J., Poitras, C. B. & Lipson, M. Silicon nanostructure cloak operating at optical frequencies. Nat Photon 3, 461–463 (2009).
Ergin, T., Stenger, N., Brenner, P., Pendry, J. B. & Wegener, M. Three-dimensional invisibility cloak at optical wavelengths. Science 328, 337–339 (2010).
Ma, H. F. & Cui, T. J. Three-dimensional broadband ground-plane cloak made of metamaterials. Nat Commun 1, 21 (2010).
García –Vidal, F. J., Martín –Moreno, L., Ebbesen, T. W. & Kuipers, L. Light passing through subwavelength apertures. Rev Mod Phys 82, 729–787 (2010).
Shen, J. T., Catrysse, P. B. & Fan, S. Mechanism for Designing Metallic Metamaterials with a High Index of Refraction. Phys Rev Lett 94, 197401 (2005).
Shin, J., Shen, J. T., Catrysse, P. B. & Fan, S. Cut-Through Metal Slit Array as an Anisotropic Metamaterial Film. IEEE Journal of Selected Topics In Quantum Electronics 12, 1116 (2006).
Belov, P. A. & Silveirinha, M. G. Resolution of subwavelength transmission devices formed by a wire medium. Phys Rev E 73, 056607 (2006).
Silveirinha, M. G., Belov, P. A. & Simovski, C. R. Ultimate limit of resolution of subwavelength imaging devices formed by metallic rods. Opt Lett 33, 1726–1728 (2008).
Shvets, G., Trendafilov, S., Pendry, J. B. & Sarychev, A. Guiding, focusing and sensing on the subwavelength scale using metallic wire arrays. Phys Rev Lett 99, 053903 (2007).
Kawata, S., Ono, A. & Verma, P. Subwavelength colour imaging with a metallic nanolens. Nat Photon 2, 438–442 (2008).
Jung, J., García-Vidal, F. J., Martín-Moreno, L. & Pendry, J. B. Holey metal films make perfect endoscopes. Phys Rev B 79, 153407 (2009).
Zhu, J., Christensen, J., Jung, J., Martin-Moreno, L. & Yin, X. A holey-structured metamaterial for acoustic deep-subwavelength imaging. Nat Physics 7, 52–55 (2011).
Silveirinha, M. G. & Engheta, N. Transporting an image through a subwavelength hole. Phys Rev Lett 102, 103902 (2009).
Morgado, T. & Silveirinha, M. G. Transport of an arbitrary near-field component with an array of tilted wires. New J Phys 11, 083023 (2009).
Silveirinha, M. G. & Engheta, N. Sampling and squeezing electromagnetic waves through subwavelength ultranarrow regions or openings. Phys Rev B 85, 085116 (2010).
Alù, A., Aguanno, G. D., Mattiucci, N. & Bloemer, M. J. Plasmonic Brewster Angle: Broadband Extraordinary Transmission through Optical Gratings. Phys Rev Lett 106, 123902 (2011).
Rahm, M., Schurig, D., Roberts, D. A., Cummer, S. A., Smith, D. R. & Pendry, J. B. Design of electromagnetic cloaks and concentrators using form-invariant coordinate transformations of Maxwells equations. Photonics and Nanostructures-Fundamentals and Applications 6, 87–95 (2008).
Navau, C., Prat-Camps, J. & Sanchez, A. Magnetic energy harvesting and concentration at a distance by transformation optics. Phys Rev Lett 109, 263903 (2012).
Chen, H. Y. & Chan, C. T. Electromagnetic wave manipulation by layered systems using the transformation media concept. Phys Rev B 78, 054204 (2008).
Chen, H. Y. & Chan, C. T. Transformation media that rotate electromagnetic fields. Appl Phys Lett 90, 241105 (2007).
Vasic, B., Isic, G., Gajic, R. & Hingerl, K. Controlling electromagnetic fields with graded photonic crystals in metamaterial regime. Opt Express 18, 20321–20333 (2010).
Han, S., Xiong, Y., Genov, D., Liu, Z., Bartal, G. & Zhang, X. Ray optics at a deep-subwavelength scale: a transformation optics approach. Nano Lett 8, 4243 (2008).
Kildishev, A. V. & Narimanov, E. E. Impedance-matched hyperlens. Opt Lett 32, 3432–3434 (2007).
Acknowledgements
This work is supported by National Science Foundation of China for Excellent Young Scientists (grant no. 61322504), the Foundation for the Author of National Excellent Doctoral Dissertation of China (grant no. 201217), the National Natural Science Foundation of China (grant nos. 11004147, 11104198 and 11474212) and the Priority Academic Program Development (PAPD) of Jiangsu Higher Education Institutions. H.C. would like to thank Winsley Yang's effort to polish the English.
Author information
Authors and Affiliations
Contributions
H.C. conceived the idea. H.C., M.M.S. and L.X. did the theoretical calculations and the numerical simulations. B.H., S.L. and L.X. fabricated the samples and did the experimental measurements. B.H. supervised the experimental part. H.C. supervised the whole project. H.C. and B.H. wrote the manuscript.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Electronic supplementary material
Supplementary Information
Supplementary Information
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article's Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder in order to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Sadeghi, M., Li, S., Xu, L. et al. Transformation optics with Fabry-Pérot resonances. Sci Rep 5, 8680 (2015). https://doi.org/10.1038/srep08680
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep08680
This article is cited by
-
Controlling water waves with artificial structures
Nature Reviews Physics (2024)
-
Controlling electromagnetic surface waves with conformal transformation optics
Communications Physics (2023)
-
Designing Electromagnetic Field Rotators with Homogenous and Isotropic Materials
Plasmonics (2021)
-
Illusion Properties in Perfect Cylindrical Devices
Plasmonics (2020)
-
Transformation devices with optical nihility media and reduced realizations
Frontiers of Physics (2019)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.