Introduction

Coordination of the activity within and between the brain's cellular networks achieved through synchronization has been invoked as a functional feature of normal and abnormal temporal dynamics1, the integration and segregation of information2,3 and of the emergence of neural rhythms4,5. Macroscopic rhythms like pacemaker activity, rhythmic motor pattern generation, alpha, theta and gamma cortical rhythm, are well-known examples of collective coordinated neural dynamics. Harmful examples of the rhythmic collective dynamics of large brain cell networks are the pathological activities found in epilepsies and Parkinson's disease6,7,8,9,10,11. Although the precise origin of these rhythms in each specific phenomenon is still debated1, it is often hypothesized that they emerge from the coordinated activity of many thousands of neurons4,5. Therefore, in theoretical and computational modeling this collective brain dynamics is frequently considered as a macroscopic endogenous (self-sustained) oscillation12,13. In particular, this model description is exploited in theoretical studies12,14,15,16,17,18,19 searching for efficient algorithms to suppress certain brain oscillations, with the ultimate goal of developing novel techniques for pathological brain rhythm cancellation (for instance, via deep brain stimulation20,21).

The reductionist approach treating a large neuronal network as a single active unit stems from numerous studies in nonlinear dynamics, which state that a collective oscillatory mode of a large population of highly interconnected active units emerges via a Hopf-like bifurcation, so that the population can be considered in this context as a macroscopic periodic or chaotic self-sustained oscillator22,23. Recently, a novel computational model of the gamma rhythm was developed, showing that it is possible to connect microscopic (synaptic) properties of neurons with the macroscopic gamma oscillation. Importantly for the current study, the authors derived phase response curves (PRC) and entrainment properties of the gamma rhythm under external stimulation24. Evidence from in vitro experiments in the rat hippocampus strongly suggest that a macroscopic oscillator emergences at least in the important case of the gamma rhythm (see e. g, Akam et. al.25 and references therein). However, the validity of this reductionist approach has never been tested in direct in vivo experiments. To bridge this gap, we examined stimulated brain activity in the thalamocortical circuit of epileptic rats.

Our approach is straightforward. Synchronization theory26,27,28,29,30,31 predicts that if a system can be modeled as a noisy limit cycle or weakly chaotic oscillator, then it should react to a rhythmical perturbation by adjusting its frequency. If the frequency of the oscillator, Ω, is initially close to that of the external stimulation, ω, then stimulation of sufficient strength leads to frequency locking, i.e. to equality of the frequencies. Importantly, the frequency locking condition ω = Ω shall be preserved for a range of amplitudes I and frequencies ω of the forcing. The domain of locking in the I - ω plane is known as the Arnold tongue. Generally, the condition of frequency locking implies a rational relation between two frequencies, i.e. Ω: ω = n: m, where n, m are integers. For noisy oscillators the condition of locking is not fulfilled exactly, however, the locking domains can be revealed for real-world oscillators as well, at least for the main locking region n = 1, m = 1, see e.g. the results on entrainment of the human heart rate by periodic acoustic and visual stimulation32. The ability to be synchronized, or entrained, by an external drive is a general property of endogenous oscillators. According to the theory, this is also valid for macroscopic oscillations of ensembles consisting of many interacting units33,34,35, in our case neurons. Hence, if the above formulated reductionist approach is valid, the brain rhythm shall exhibit frequency locking to external force. We corroborate this approach for the case of the sustained rhythmic activity of absence epileptic seizures. We investigate a specific type of paroxysmal activity (spike and wave discharges (SWD)) induced in rats using drugs. The rhythmic activity notably appears in the thalamocortical circuit. We demonstrate that periodic pulse stimulation of this circuit leads to frequency locking and thus present strong evidence that it can be considered as a macroscopic self-sustained oscillation. This result is important, e.g., for understanding mechanisms of possible control of pathological brain activity15,16.

Results

We first investigated the cortical and thalamic responses at constant amplitude of stimulation, but at different frequencies and subsequently analyzed the responses as the amplitude of the stimulation was varied, so that the possible Arnold tongues could be generated. A schematic illustration of the experimental setting is depicted in Fig. 1, showing the stimulation and measurement electrodes (including histology of the corresponding brain sections) as well as simultaneous recordings from cortex and thalamus of a rat experiencing SWD. Examples of recorded activity with and without the electrical stimulation are presented in Fig. 2. Quantification of the SWD frequency during the imposed stimulation shows the characteristic synchronization plateau (Fig. 3), which is an indication that the cortical network is frequency-locked to external stimulation in the range of 6 to 15 Hz, depending on the amplitude of the stimulus: higher injected current increased the range of frequency-locking of the SWD. This measurements also provided the Arnold tongues, typical of noisy systems (Fig. 4). Similar results were obtained with either thalamic or cortical stimulation, as well as with another rat model of absence-like seizures36 that presents a different frequency of the SWD at 3–4 Hz (results not shown here).

Figure 1
figure 1

Stimulation and measurement electrodes.

(A) Schematic illustration of the location of electrodes. An implanted electrode at the thalamus is connected to a square pulse stimulator that generates a periodic pulse train. Simultaneously, a cortical electrode records activity in frontal areas. The reverse configuration was also used, with the simulation electrode in the cortex and the recording electrode in the thalamus. The trace at the measurement electrode shows the typical spike and wave discharges (SWD) observed during a seizure. (B) Histology on two cresyl violet-stained brain sections depicting the location of the cortical and thalamic electrodes. (C) Simultaneous recordings from cortex and thalamus of a rat experiencing spontaneous and recurrent SWD.

Full size image
Figure 2
figure 2

Illustrative examples of the effect of stimulation on the SWD responses at several frequencies.

Traces were obtained from the cortex in response to thalamic stimulation, in different rats. Arrows are depicted on top of each trace in order to help counting the number of spike and waves discharges (SWD) in 1 sec recordings. (A) Stimulation at four different frequencies (6, 8, 9 and 10 Hz). Time is running in the vertical direction, from the top to the bottom of the figure, so, for example, the second row shows traces before, during and after stimulation at 8 Hz. The spontaneous oscillations in the traces chosen for illustration (upper row) have a frequency of approximately 8 Hz (in general, the frequency range of the spontaneous oscillation is of 7 to 8 Hz). The traces obtained during stimulation are shown in the middle row. Stimulation at 6 Hz clearly slows down the frequency of SWD. Slight changes are observed for the stimulation at 8 Hz (a special case, being the closest to the spontaneous oscillation frequency), with a small increase of frequency of SWD to about the same frequency of stimulation. For illustration, in the lower row it is shown that after stimulation at 8 Hz the SWD slows down to a value within the range of the spontaneous oscillation (7~8 Hz). In the examples shown at 9 Hz and 10 Hz, stimulation entrains the frequency of the response and also changes substantially the recorded waveforms. (B) Stimulation at 4 Hz shows an approximately 2:1 frequency locking of the oscillation (around 8 SWD in one second).

Full size image
Figure 3
figure 3

Frequency locking of the SWD with increasing stimulation intensity.

The three panels depict frequency locking to external stimulation in three rats. The x-axis (ω) is the frequency of the periodic stimulation and the y-axis is the difference between the SWD frequency (Ω) and the imposed frequency (ω). In each panel, each curve was obtained at a different stimulation current. Curves were shifted for better visibility, according to the stimulation amplitudes (the curve at the top corresponds to the largest stimulation amplitude). The dotted horizontal lines show the zero level for each curve; these lines correspond to perfect locking between Ω and ω, i.e. to the fulfillment of the condition ω = Ω. Notice the wider frequency locking as the stimulation intensity increases.

Full size image
Figure 4
figure 4

Arnold tongues.

The three panels depict what can be considered as Arnold tongues in three different rats. Right column: the Arnold tongues in 3D. The x-axis (I) is the intensity of the stimulation current, y-axis (ω) is the frequency of the periodic stimulation and the z-axis is the difference between the frequency of SWD (Ω) and the imposed frequency ω. Data points marked as asterisks (*) in red are points inside the Arnold tongue, which is defined as the region where |Ω - ω| < 1 Hz. Data points marked as asterisks (*) in blue are points outside the Arnold tongue. The color surface is an interpolation of the data using a standard interpolation algorithm. Left column: projection of the Arnold tongue on the plane I - ω (2D Arnold tongue). Data points marked as black circles with a red asterisk inside are points inside the Arnold tongue, whereas those marked as black circles without asterisks are points outside the Arnold tongue.

Full size image

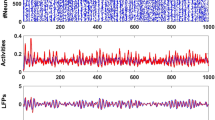
Figure 5 shows the dependence of evoked local field potentials (eLFP) on the amplitude of stimulation. A few examples of eLFP for various current amplitudes and the corresponding local field potential recording of spontaneous SWD are shown. It can be seen (see figure legend for details) that for low stimulation currents, the eLFP is much smaller than the SWD amplitude and thus will not interfere with the detection of the wave in the SWD. However, for very large stimulation currents the eLFP and the natural SWD will superimpose and will make it impossible to differentiate between them.

Figure 5
figure 5

Evoked local field potentials.

Evoked local field potentials (eLFP) for four different current amplitudes and corresponding recording of SWD. Left panels: recordings of activity when SWD is not present. In this case there is a clear superposition of the low amplitude spontaneous non-rhythmic activity and higher amplitude eLFP (easily identified in the traces for its spike-like appearance). Right panels: traces of activity during SWD in the same recording period (without stimulation), in order to compare the amplitudes of the eLFP (left panels) with the spontaneously occurring SWD. Notice, in the left panel, that the amplitude of the eLFP increases with stimulation current.

Full size image

Discussion

In this study we have measured the electrophysiological response of the thalamocortical network in a rat model of epilepsy during seizure activity. We observed frequency changes in seizure traces (periodic spike and wave discharges (SWD), characteristic of absence seizures) when the thalamocortical network was perturbed by an external periodic stimulation. Specifically, we found frequency-locking of the SWD to the frequency of the stimulation.

Essential for this type of in vivo experiments is that the stimulation produces an evoked local field potential (eLFP), measured by the recording electrode. Thus the question arises as to whether the eLFP and not the “spontaneous” spike, is what we quantify as the “spike” in the SWD. In other words, the local field potential evoked by the stimulation electrode is superposed onto the spontaneous oscillation (already present at the measuring electrode) to generate the recorded SWD. This could lead to confusion, because we are calculating the period of the oscillations as the time between spikes in the SWD and the evoked response could in principle interfere with the calculation of the oscillation period. We will clarify this issue here and see how this relates to the theory of coupled oscillators. The crucial point is that the relative size of the evoked response (as compared to the spontaneous oscillation) is proportional to the intensity of the stimulation current. To illustrate these matters, Fig. 5 depicts the eLFPs at 4 different current amplitudes and, for comparison, the spontaneous SWD occurring at those times. The eLFP can be distinguished at the recording electrode whenever the spontaneous activity is non-periodical (Fig. 5, left panels), because the evoked response is smaller than the SWD (compare with Fig. 5 right panels). However, when the frequency of stimulation is high enough (>10 Hz), the stimulation changes the frequency of the response and also changes the recorded waveforms, as shown in Figure 2 at 10 Hz (and at frequencies higher that 10 Hz, data not shown).

This can be easily understood in terms of the theory of self-sustained oscillators26, which predicts two qualitatively different transitions to synchronization for a forced self-sustained oscillator, depending on the strength of the coupling or forcing. For weak forcing, the transition to synchronization occurs via phase locking: a small external force affects mainly the phase of oscillations (and, hence also its frequency), but not their amplitude, so that the phase difference between oscillators is constant inside the synchronization region. A stronger forcing influences both the phase and the amplitude. As a result, transition to synchrony occurs via suppression of natural oscillation, while the oscillation with the forcing frequency is imposed. Thus, the theory predicts different pictures for small and large amplitudes of stimulation and indeed our observations are in full agreement with these expectations. For example, synchronization at frequencies higher than 10 Hz (Fig. 2) can be achieved by increasing the external forcing (strong forcing regime), as compared to synchronization at around the natural frequency (7–8 Hz, weak forcing regime), because, as can be seen from Figs. 3 and 4, to achieve synchronization at frequencies distant from the natural frequency, a stronger forcing is required. This explains why the shape of the recorded waveforms is also changed at higher frequencies: in the strong forcing regime amplitude is also affected. In view of this, it is clear that the eLFP is weak at forcing frequencies near the natural frequency and it does not affect the shape of the recorded SWD. Conversely, at stimulation frequencies distant from the natural frequency, the recorded SWD almost coincides with the eLFP, as the oscillation with the forcing frequency is imposed. In other words, the distinction between eLFP and SWD disappears in the strong forcing regime and any possible ambiguity as to how to distinguish the “spontaneous spike” from the “evoked spike” in the recorded SWD is resolved. Beyond the technical issue of spike measurement, the observation of weak and strong forcing regimes in our data set further confirms an explanation based on oscillation theory. Notice that, typical for noisy systems, only the main locking region is well pronounced, therefore we have systematically looked at the 1:1 locking. However, an example in Fig. 2B indicates that 2:1 locking is possible as well: here, two SWDs correspond to one stimulus.

Interestingly, the Arnold tongues are strongly asymmetrical, in agreement with the prevalence of phase advancement over phase delay in the resetting of cortical oscillations by thalamic stimulation36. In previous work, spontaneous SWDs were induced in rats using the same absence seizure model as in the current study, but the stimulation protocol differed in that intracerebral electrical stimulation did not consist of periodic pulses, but of pulses given at random times in order to allow for the proper estimation of phase response curves (PRC), which were shown to be strongly asymmetrical (see Fig. 3 in Perez Velazquez et. al., 200736). Because we used periodic pulses in the current study, PRCs as those aforementioned were not easily computed. We emphasize here that a stimulation protocol designed to study phase locking and to reconstruct Arnold tongues should consist of periodic pulses and is therefore not well suited for PRC exploration, since a good quality PRC requires sampling on the entire range of stimulation phases, a condition that is not necessarily fulfilled when the stimulation is periodic. The propensity for advancement of the cortical activity in response to thalamic stimulation is conceivable if the phenomenon known as the "thalamic augmenting response" is considered, that is, the net result of thalamic inputs to cortex is an enhancement of the cortical excitation37. On the other hand, because of the recurrent activity in cortical circuits, specially the inhibitory neurons projecting to pyramidal cells, stimulation that arrives in the late phase of the cycle of the SWD will conceivably result in the inhibitory potential retarding the next wave and thus a delay may be expected for late phase of stimulation, as was found in the PRCs in Perez Velazquez et. al., 200736. Furthermore, it has been shown that strictly positive PRCs are expected in neural models where oscillations arise through a saddle-node bifurcation41.

Taken together, the observed results represent clear evidence of frequency-locking in the thalamocortical circuit in this rat model of periodic and synchronous paroxysmal discharges, a model that shares many features with human absence seizures.

In conclusion, we have experimentally observed frequency locking for the first time and obtained Arnold tongues in experiments with stimulated brain activity in vivo. Specifically, we found that the thalamocortical circuit in rat models of paroxysmal activity shows the phenomenon of frequency-locking when stimulated by periodic electrical pulses, at least in a certain frequency range. In this way we have confirmed the hypothesis that a macroscopic cell network in the brain behaves as a self-sustained oscillator. This finding is important since an increasing body of research relies on this hypothesis. Further, these results have implications for mechanisms of control of pathological brain rhythm cancellation12,14,18,38. In particular, our finding may constitute the basis for developing techniques for seizure prevention and cancellation39.

Methods

Electrode implantation and in vivo intracerebral recordings

Bipolar electrodes (Plastics One, Roanoke, Virginia, USA) were implanted chronically into specific brain areas of Long Evans rats (50–55 days old) using stereotactic surgery (Fig. 1B). The coordinates of electrode implantation were: into the thalamus, B-3.3, ML 2, D 6.4 and into frontal cortex, B 0.2, ML 3, D 2.1. The electrodes were fixed to the skull using dental acrylic. After a recovery period of 4–5 days, animals were placed in an electrically screened Plexyglass chamber for recordings. The recording electrodes were connected to an AI 402 x 50 Ultra-low Noise differential amplifier (Axon Instruments, Foster City, CA), a CyberAmp 380 signal conditioner (Axon Instruments) and an analog-digital converter MP100 (Biopac, Harvard Instruments, St. Laurent, Quebec, Canada). Recordings were acquired at 200 Hz. Intracerebral electrical stimulation was achieved using a Grass square pulse stimulator S88K (Grass Instruments), equipped with a stimulation isolation unit that delivered square current pulses in the range 0.01 to 15 mA. Histological examination (cryostat sections of paraformaldehyde-fixed brains) of the rat brains at the end of the experiments confirmed the location of the electrodes. Initial and preliminary electrophysiological data analysis was done using the software package Acknowledge (Biopac, Harvard Instruments). Manipulations of the rats were performed according to the protocols approved by the Animal Care Committee of the Hospital for Sick Children.

Induction of spontaneous SWD in rats

To induce rhythmic discharges (SWD), ten Long-Evans rat pups were treated with a subcutaneous dose of the cholesterol synthesis inhibitor AY9944 (7.5 mg/kg), every 6 days from postnatal day 2 to P20, as described in detail previously36,40. This treatment promotes chronic spike-and-wave (SWD) paroxysmal activity at frequencies of 7–8 Hz. These events last throughout the life of the animal. For the experiments, rats were used from postnatal ages 55 up to 70 days.

Data analysis and description of a typical experiment

To quantify the frequency of the SWD (see Figs. 1 and 2 for typical experimental traces obtained), the spikes were counted in 1 sec windows. Spike detection was performed with the use of a pattern recognition algorithm (an automatic spike detection program coded in MATLAB, http://www.mathworks.com/matlabcentral/fileexchange/25500-peakfinder) and also by visual inspection of all the data sets. Only peaks within the SWD were considered, and, as can be inspected in the figures, those were very clearly distinguishable. Once the SWD peaks were detected, the period was calculated as averaged times between consecutive spikes. Rat brains were electrically stimulated during SWD activity either in the thalamus or the cortex, while the intracerebral activity was simultaneously recorded as local field potentials in the cortex or thalamus, respectively (Fig. 1A). The stimulation had frequencies in the range of 1–15 Hz. The typical activity during SWD, shown in Fig. 1C, occurs in cortex and thalamus at a frequency of approximately 7 to 8 Hz.

A typical experiment was conducted as follows. The rat was placed in the recording chamber and the activity recorded from the two electrodes (one located in the thalamus and the other in the cortex using the specific stereotaxic coordinates mentioned before). After being certain that SWD could be recorded clearly -which took a variable period of time, between 10 and 30 minutes- one electrode was chosen as the recording electrode and the other was connected to the Grass stimulator. A few single pulses at different amplitudes were injected to assess the evoked response to the stimulation. This is important because the amplitudes needed to observe a minimal response in the recording electrode varied amongst animals (see for instance the amplitude range in the plots in Fig. 3). When a minimal evoked response to a certain current intensity was noted, it was chosen as the initial current amplitude for the experiment. Once the current intensity was set, stimulation at the fixed amplitude and a specific frequency commenced shortly (1–3 seconds) after an SWD appeared in the recordings. It should be noted that each SWD had a variable duration from animal to animal and the durations of sustained SWDs used in these studies varied between 8–30 seconds. For example, if a rat displayed very short durations of sustained SWD (e.g. 2–4 seconds), those recordings were not used in our experiments, as the electrical stimulation had to be applied for at least a few seconds in order to obtain a reliable computation of the frequency of the SWD. After a few stimulations at the specified frequency were completed, a new frequency was chosen, following the same operations as in the procedure described above. Normally, the starting frequency and amplitudes of the injected current were the lowest possible, for instance the frequency started at 1 Hz, then 2 Hz, 3 Hz, etc. The current injected varied from animal to animal, to ensure that not too large currents were used, in order to prevent possible significant alterations of the synaptic connections that could be caused by large currents or high frequencies. When the full range of stimulation frequencies was completed, the next current amplitude level was used. A typical experiment lasted 2–3 hours, after which the rat was placed back in its room and used in following days. Because of the nature of these paroxysmal discharges that resemble absence seizures in humans, the animals did not seem to experience discomfort and were available for as many days as needed.