Abstract
Gauge theory plays the central role in modern physics. Here we propose a scheme of implementing artificial Abelian gauge fields via the parametric conversion method in a necklace of superconducting transmission line resonators (TLRs) coupled by superconducting quantum interference devices (SQUIDs). The motivation is to synthesize an extremely strong effective magnetic field for charge-neutral bosons which can hardly be achieved in conventional solid-state systems. The dynamic modulations of the SQUIDs can induce effective magnetic fields for the microwave photons in the TLR necklace through the generation of the nontrivial hopping phases of the photon hopping between neighboring TLRs. To demonstrate the synthetic magnetic field, we study the realization and detection of the chiral photon flow dynamics in this architecture under the influence of decoherence. Taking the advantages of its simplicity and flexibility, this parametric scheme is feasible with state-of-the-art technology and may pave an alternative way for investigating the gauge theories with superconducting quantum circuits. We further propose a quantitative measure for the chiral property of the photon flow. Beyond the level of qualitative description, the dependence of the chiral flow on external pumping parameters and cavity decay is characterized.
Similar content being viewed by others
Introduction
Circuit quantum electrodynamics (QED)1,2,3,4 is the realization of cavity QED5,6 in superconducting quantum circuits. It employs the superconducting coplanar transmission line resonators (TLRs)1,2 to substitute the standing-wave optical cavities and the superconducting qubits7,8,9,10 to replace the atoms. Due to its flexibility and scalability, this on-chip architecture has been regarded as a promising platform for quantum computation4 and quantum simulation15,16. Recently, several theoretical schemes have been proposed to generate artificial gauge fields for microwave photons and polaritons11,12,13,14 in circuit QED lattices15,16. While the idea of synthesizing gauge fields was first proposed and realized in the context of ultracold atoms17,18,19 and magneto-optical systems20, circuit QED takes the advantages of individual addressing and in situ tunability of circuit parameters4,15,16. Moreover, the effective strong photon-photon repulsion can be induced through a variety of mechanisms, including electromagnetically induced transparency (EIT)21,22,23, Jaynes-Cummings-Hubbard (JCH) nonlinearity24,25 and nonlinear Josephson coupling26,27,28. Combining the strong photon correlation with the synthetic gauge fields, the circuit QED system is showing prospective potential in the investigation of bosonic fractional quantum Hall liquids29,30 and nontrivial topological edge states for microwave photons31.
In the pioneering work13 and its generalization14, a method of generating effective magnetic fields for polaritons in a two dimensional cavity lattice has been proposed. For each site on the lattice, the mixing phase between the atomic and photonic components of the polariton is controlled by an EIT type modulation of the atom trapped in the cavity and the inter-site polariton hopping is induced by the untunable evanescent coupling between neighboring cavities. When hopping from one particular site to its neighbor, the polariton acquires a hopping phase which is the difference of the mixing phases subjected to the two neighboring sites. To obtain nontrivial gauge fields, the hopping along the horizontal and vertical directions should be controlled independently and two-mode cavities (TMCs) and double EIT processes are consequently required. The construction and pumping of the complicated multi-level artificial atoms are still challenging in current experimental setup. There is also another scheme proposed in which a passive circulator is used to induce nontrivial hopping phases between TLRs capacitively connected to it12 through a virtual-resonant process. Due to its dispersive nature, this scheme is suitable to construct Kagomé and honeycomb lattices with coordination number three because the circulator induces effective photon hopping between any two of the TLRs connected to it. When applied to other lattice configurations with coordination number larger than three (e. g. square lattice with coordination number four), this scheme will result in unwanted cross-talk.
In this manuscript, we consider an alternative mechanism of implementing artificial Abelian gauge fields and propose a minimum circuit to demonstrate this method. Our work is inspired by the laser assisted tunneling technique used in ultracold atoms17 and recent works of Josephson-embedded circuit QED systems28,33,34,35. We consider a necklace consisting of three TLRs coupled by superconducting quantum interference devices (SQUIDs)26,28,32,33 which can be harmonically modulated. With appropriate modulating pulses, effective parametric photon conversion between eigenmodes of the necklace can be induced34, which manifests itself as photon hopping between neighboring TLR sites. This modulation in turn leads to an accumulated hopping phase during the hopping process, which can be regarded as an effective magnetic field imposed on the photons. As our method endows hopping phases directly to the links between TLRs, we expect that the experimental setup of our scheme is much simpler because the complicated double EIT pumping is not necessary. In addition, since our scheme does not rely on the dispersive mechanism, the above-mentioned cross-talk difficulty can also be circumvented. Moreover, the effective hopping strength in our scheme can be controlled by the modulating pulses. Such advantage may offer potential facilities in the future study of the competition between synthetic gauge fields, photon hopping and Hubbard repulsion.
We further study the chiral photon flow dynamics of the necklace, which is a direct evidence of the breaking of time reversal symmetry (TRS) in the proposed circuit. We numerically simulate the photon flow dynamics in the presence of decoherence based on reported experimental data34,36,37. Our results imply that the unidirectional character of the photon flow survives in the cavity decay. The feasibility of detecting such phenomena with the recently-developed photon detection technique34,38,40 is also discussed. Moreover, to quantitatively describe the chiral flow, we introduce the concepts of photon position vector and chiral area. We show that the direction and the strength of the chiral photon flow can be represented by the chiral area which is the directed area swept by the photon position vector in a given time. With the proposed quantitative measure, we quantify the chiral flow character in general cases and investigate its detailed dependence on external pumping and decoherence processes.
Results
Implementing artificial gauge field with dynamic modulation method: the theoretical model
We start from a photon hopping process between three cavities described by the following Hamiltonian

where  are the annihilation/creation operators of the ith site for i = 1, 2, 3, gij are the i ↔ j hopping rates and θij are the corresponding hopping phases. We can imagine that there is a photon initially prepared in the cavity 1 and hopping on the cavity necklace. When finishing the 1 → 3 → 2 → 1 circulation, the photon accumulates a phase θΣ = θ12 + θ23 + θ31, which is similar to the Aharonov-Bohm phase of an electron circulating in an external magnetic field. Consequently, θΣ can be regarded as an artificial magnetic field imposed on the charge-neutral photon and the TRS of this circuit keeps intact if and only if
are the annihilation/creation operators of the ith site for i = 1, 2, 3, gij are the i ↔ j hopping rates and θij are the corresponding hopping phases. We can imagine that there is a photon initially prepared in the cavity 1 and hopping on the cavity necklace. When finishing the 1 → 3 → 2 → 1 circulation, the photon accumulates a phase θΣ = θ12 + θ23 + θ31, which is similar to the Aharonov-Bohm phase of an electron circulating in an external magnetic field. Consequently, θΣ can be regarded as an artificial magnetic field imposed on the charge-neutral photon and the TRS of this circuit keeps intact if and only if  11,12. To break the TRS, we synthesize non-trivial θ12, θ23 and θ31 by the dynamic modulation method39: we consider a three-cavity Hamiltonian
11,12. To break the TRS, we synthesize non-trivial θ12, θ23 and θ31 by the dynamic modulation method39: we consider a three-cavity Hamiltonian

with


where ωi is the eigenfrequency of the ith cavity and Ωij(t) is the coupling constant between the ith and jth cavities. Here we assume that Ωij(t) can be tuned harmonically and in situ (we will discuss the physical realization in the next subsection). Moreover, we assume that the parameters in  satisfy the far off-resonance condition:
satisfy the far off-resonance condition:

In the first step we consider the 1 ↔ 2 hopping. If Ω12(t) is static, the 1 ↔ 2 photon hopping can hardly be induced because the two cavities are far off-resonant. Meanwhile, we can implement the effective 1 ↔ 2 photon hopping by modulating Ω12(t) dynamically as

Physically, Ω12(t) carries energy quanta filling the gap between the two cavity modes. For a photon initially placed in the 1st cavity, it can absorb an energy quantum ω2 − ω1 from the 1 ↔ 2 link, convert its frequency to ω2 and hop finally into the 2nd cavity. We can further describe this process in a more rigorous way: in the rotating frame with respect to  ,
,  becomes
becomes

because the other terms are fast oscillating and thus are safely neglected. From Eq. (7), we notice that both the effective hopping strength and the hopping phase can be controlled by the modulating pulse Ω12(t). Similarly, we can induce the effective 2 ↔ 3 and 3 ↔ 1 hopping process by modulating Ω23(t) and Ω31(t) as


Summarizing the three pulses up, we get

which directly reproduces the model (1).
The superconducting circuit implementation: a SQUID-coupled three-TLR necklace
Here we show explicitly the implementation of Eq. (1) in a circuit QED necklace. We propose a circuit consisting of three TLRs with different lengths Ln but the same capacitance c and inductance l per unit length, coupled by three grounding SQUIDs with capacitance CJα and maximal Josephson coupling energy Eα for n = 1, 2, 3 and α = a, b, c, as shown in Fig. 1(a) (this architecture has also been exploited to study the entanglement generation through dynamic Casimir effect recently35). For each of the SQUID loops, an external static flux bias  is added to modulate the effective Josephson coupling energy as
is added to modulate the effective Josephson coupling energy as  with Φ0 = h/2e the flux quantum. We assume that the inductance/capacitance of the resonator is much bigger than the inductance/capacitance of the SQUIDs such that the following inequalities hold:
with Φ0 = h/2e the flux quantum. We assume that the inductance/capacitance of the resonator is much bigger than the inductance/capacitance of the SQUIDs such that the following inequalities hold:


where  is the effective inductance of the αth SQUID for α = a, b, c, L = L1 + L2 + L3 is the total length of the TLR necklace and ΔL = min{|Li − Lj|, i ≠ j} characterizes the length difference between the TLRs. Focusing only on the lowest three modes, this necklace can be described by the Hamiltonian
is the effective inductance of the αth SQUID for α = a, b, c, L = L1 + L2 + L3 is the total length of the TLR necklace and ΔL = min{|Li − Lj|, i ≠ j} characterizes the length difference between the TLRs. Focusing only on the lowest three modes, this necklace can be described by the Hamiltonian

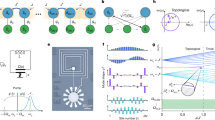
where ωm is the eigenfrequency of the mth eigenmode for m = 1, 2, 3 and  are the corresponding annihilation/creation operators. While Eq. (13) is derived in detail in Methods, we can explain the mode structure of the necklace in an intuitive way. The presence of the grounding SQUIDs can modify the eigenmodes of the individual TLRs and induce the TLR-TLR coupling. From the point of view of TLR 1, the SQUID a plays the role of a shortcut of TLR 2, because the current coming from TLR 2 will largely flow through SQUID a directly to the ground, without crossing TLR 1. This allows us to define separated and localized modes for the TLR necklace: due to the small inductances of the grounding SQUIDs, the edges of the TLRs can be regarded as grounding nodes and the lowest three eigenmodes can be approximated by the three individual λ/2 modes of the TLRs. For the mth eigenmode, we calculate its normalized node flux distribution function fn,m(x) in the nth TLR based on data from recent experiments34,36,37 and study its localization property versus the Josephson coupling energies of the grounding SQUIDs. For the TLRs, the circuit parameters are chosen as c = 1.6 × 10−10 F · m−1, l = 4.08 × 10−7 H·m−1, L1 = 6 mm, L2 = 7 mm and L3 = 8 mm. For the grounding SQUIDs, we choose the effective critical currents Iα = 2πEJα/Φ0 of the three grounding SQUIDs on the level of Iα ∈ [0.5 μA, 4 μA] for α = a, b, c. As shown in Fig. 1(b) and 1(c), larger critical currents lead to better localization, this is consistent with our previous description of the roles played by the grounding SQUIDs. With proper choice of the parameters, the eigenmode amplitudes |fn,m(x)|2 become sufficiently large only for n = m while negligible for n ≠ m.
are the corresponding annihilation/creation operators. While Eq. (13) is derived in detail in Methods, we can explain the mode structure of the necklace in an intuitive way. The presence of the grounding SQUIDs can modify the eigenmodes of the individual TLRs and induce the TLR-TLR coupling. From the point of view of TLR 1, the SQUID a plays the role of a shortcut of TLR 2, because the current coming from TLR 2 will largely flow through SQUID a directly to the ground, without crossing TLR 1. This allows us to define separated and localized modes for the TLR necklace: due to the small inductances of the grounding SQUIDs, the edges of the TLRs can be regarded as grounding nodes and the lowest three eigenmodes can be approximated by the three individual λ/2 modes of the TLRs. For the mth eigenmode, we calculate its normalized node flux distribution function fn,m(x) in the nth TLR based on data from recent experiments34,36,37 and study its localization property versus the Josephson coupling energies of the grounding SQUIDs. For the TLRs, the circuit parameters are chosen as c = 1.6 × 10−10 F · m−1, l = 4.08 × 10−7 H·m−1, L1 = 6 mm, L2 = 7 mm and L3 = 8 mm. For the grounding SQUIDs, we choose the effective critical currents Iα = 2πEJα/Φ0 of the three grounding SQUIDs on the level of Iα ∈ [0.5 μA, 4 μA] for α = a, b, c. As shown in Fig. 1(b) and 1(c), larger critical currents lead to better localization, this is consistent with our previous description of the roles played by the grounding SQUIDs. With proper choice of the parameters, the eigenmode amplitudes |fn,m(x)|2 become sufficiently large only for n = m while negligible for n ≠ m.
(a) Schematic plot of the SQUID-coupled three-TLR necklace. This circuit is constructed by three TLRs connected through the grounding SQUIDs. For each SQUID α, the SQUID loop is penetrated by a static bias flux  and a dynamic modulation pulse δΦα with α = a, b, c. Moreover, each TLR is coupled to a measurement device which can detect its photon number. The lowest three eigenfrequencies of the circuit are labeled by ω1, ω2 and ω3, respectively. (b), (c) The localization property of the eigenmodes. (c) depicts the normalized mode functions of the three lowest eigenmodes of the circuit QED necklace versus critical currents of the SQUIDs. The three panels of (c) describe the eigenmode functions corresponding to the eigenmode 1, 2 and 3 respectively. The blue solid line, green dash line and red dot-dashed line correspond to the situations of IS = Ia = Ib = Ic = 1, 2, 3 μA respectively. In addition, we set EJα/ECα = 100 with ECα = 2e2/CJα. With the chosen parameters, we get ω1/2π = 11.5 GHz, ω2/2π = 9.5 GHz and ω3/2π = 8.2 GHz for IS = 3 μA. In (b), we quantify the localization property of the mth eigenmode by Em/ωm where Em is the energy stored in the mth TLR for m = 1, 2, 3. The critical current IS of the SQUIDs varies from 0.5 μA to 4 μA and the other parameters are chosen as the same as in Fig. 1(c). (d) Square lattice consisting of four kinds of TLRs. Four kinds of TLRs with different eigenfrequencies (red for ω1/2π = 8 GHz, orange for ω2/2π = 9 GHz, blue for ω3/2π = 10 GHz and dark blue for ω4/2π = 11 GHz) are placed in an interlaced form and coupled by grounding SQUIDs. With proper pumping pulses, only nearest-neighbor parametric photon hopping can be induced.
and a dynamic modulation pulse δΦα with α = a, b, c. Moreover, each TLR is coupled to a measurement device which can detect its photon number. The lowest three eigenfrequencies of the circuit are labeled by ω1, ω2 and ω3, respectively. (b), (c) The localization property of the eigenmodes. (c) depicts the normalized mode functions of the three lowest eigenmodes of the circuit QED necklace versus critical currents of the SQUIDs. The three panels of (c) describe the eigenmode functions corresponding to the eigenmode 1, 2 and 3 respectively. The blue solid line, green dash line and red dot-dashed line correspond to the situations of IS = Ia = Ib = Ic = 1, 2, 3 μA respectively. In addition, we set EJα/ECα = 100 with ECα = 2e2/CJα. With the chosen parameters, we get ω1/2π = 11.5 GHz, ω2/2π = 9.5 GHz and ω3/2π = 8.2 GHz for IS = 3 μA. In (b), we quantify the localization property of the mth eigenmode by Em/ωm where Em is the energy stored in the mth TLR for m = 1, 2, 3. The critical current IS of the SQUIDs varies from 0.5 μA to 4 μA and the other parameters are chosen as the same as in Fig. 1(c). (d) Square lattice consisting of four kinds of TLRs. Four kinds of TLRs with different eigenfrequencies (red for ω1/2π = 8 GHz, orange for ω2/2π = 9 GHz, blue for ω3/2π = 10 GHz and dark blue for ω4/2π = 11 GHz) are placed in an interlaced form and coupled by grounding SQUIDs. With proper pumping pulses, only nearest-neighbor parametric photon hopping can be induced.
Moreover, since the currents of two neighboring TLRs flow to the ground through the same grounding SQUID, by the modulation of the grounding SQUIDs we can establish the effective inter-TLR parametric hopping. For the 1 ↔ 2 coupling, we add an extra a. c. flux driving δΦa(t) = ΔΦa cos[(ω1 − ω2)t − θa] to the static  which induces the parametric coupling Hamiltonian (see Methods)
which induces the parametric coupling Hamiltonian (see Methods)

with ga the coupling strength between modes 1 and 2. In the rotating frame with respect to  in Eq. (13), such modulation results in the effective 1 ↔ 2 hopping which can be described by
in Eq. (13), such modulation results in the effective 1 ↔ 2 hopping which can be described by

In addition, we can add similar pumping pulses on the SQUIDs b and c to induce the 2 ↔ 3 and 3 ↔ 1 hoppings, respectively. Summing up the three modulations, we get the effective Hamiltonian

which is identical with Eq. (1) through the mappings ga → g12, gb → g23 and gc → g31. We should emphasize that ga, gb and gc can be modulated independently by the amplitudes of the a. c. pulses and the three phases θa, θb and θc are determined by the initial phases of the corresponding pulses. The range of the effective coupling strength gα can be estimated base on reported experimental data: we set Iα ∈ [1, 4] μA,  and ΔΦα/Φ0 ∈ [0.01, 0.02] for α = a, b, c. The resulted coupling strengths are in the range gα/2π ∈ [10, 30] MHz. For simplicity, in the following we consider the homogenous hopping situation gT = ga = gb = gc.
and ΔΦα/Φ0 ∈ [0.01, 0.02] for α = a, b, c. The resulted coupling strengths are in the range gα/2π ∈ [10, 30] MHz. For simplicity, in the following we consider the homogenous hopping situation gT = ga = gb = gc.
The realization and detection of the chiral photon flow
To demonstrate the presence of the synthetic gauge field we study the chiral photon flow in this necklace which is the analog of electron circulation in an external magnetic field. We initialize the necklace such that there is initially a photon in the 1st mode and numerically simulate its subsequent time evolution in the presence of decoherence using the master equation

where ρ is the density matrix of the necklace and κj is the decay rate of the jth eigenmode. The circuit parameters are chosen as the same as those used in the calculation of Figs. 1(b) and 1(c), with the pumping strength gT/2π = 20 MHz and the homogenous decay rate κ/2π = 250 kHz. In the three situations θΣ = π/2, π and 3π/2, we calculate the energy stored in the TLRs and plot our results in Fig. 2. As shown in the first panel which corresponds to θΣ = π/2, the energy population in the three TLRs exhibits clear temporal phase delay which implies that the photon is flowing unidirectionally, first from TLR 1 to TLR 2 and then from TLR 2 to TLR 3. Such chiral character is a significant demonstration of the breaking of TRS in this system. Similarly, the third panel which corresponds to θΣ = 3π/2 describes the chiral photon flow with the opposite direction. Meanwhile, the second panel implies that, in the trivial case θΣ = π, the energy initially stored in TLR 1 transfers symmetrically to its left and right. It should be emphasized that, although the cavity decay rate κ we choose is stronger compared with reported experimental data38, the chiral character of the photon flow in the first and third panel still survives. The environment causes severe photon damping but influences little on the unidirectional character of the photon dynamics. Therefore, we expect that the chiral photon flow pattern in this necklace can be realized and measured by the photon number detection technique developed in recent experiments34,38,40. For the three measurement devices shown in Fig. 1(a), we can use three phase qubits capacitively coupled to the corresponding TLRs34,38. Since the frequencies of the qubits can be adjusted by their d. c. bias currents, the initialization and the measurement of the chiral flow dynamics can be proceeded by the following steps: in the first step, we tune the frequencies of the qubits to be large off-resonance with the TLRs and prepare the qubit 1 in its excited state. In this step, the coupling between the qubits and TLRs are effectively turned off. In the second step, we tune on the qubit-TLR coupling by adiabatically tuning the qubit 1 in resonance with the TLR 1 for a duration T1 = π/2gq1 such that the excited qubit 1 emit a photon to the TLR 1 (here gqn denote the coupling strengths between TLR n and qubit n for n = 1, 2, 3). Through this manipulation, the single-photon initial state is prepared. After the initialization, we turn off the qubit-TLR coupling and turn on the external a. c. flux pumping on the grounding SQUIDs for a duration T0 during which the TLR necklace experiences the chiral photon flow. To measure the photon flow dynamics, we could prepare the three qubits all in their ground state, turn off the external a. c. flux pumping and then turn on the TLR-qubit coupling by tuning the frequencies of the qubits in resonance with the corresponding TLR modes. In this way we can load the TLR photons into the corresponding qubits and extract the evolution of photon distribution on the necklace through the measurement of the three qubits8.
Chiral photon flow in the TLR necklace in the presence of decay.
The three panels from top to bottom represent the three situations θΣ = π/2, π and 3π/2, respectively. The solid (blue), dashed (green) and dot-dashed (red) lines represent the energies stored in the TLR 1, 2 and 3, respectively. For the three grounding SQUIDs we assume that they have identical maximal critical current 5 μA and identical static flux bias  . The amplitudes of the pumping pulses are chosen as ΔΦa/b/c/Φ0 = 1.4/2.0/1.4% such that the homogeneous coupling strength gT/2π = ga/2π = gb/2π = gc/2π = 20 MHz is induced. The decay rate is chosen as κ/2π = 250 kHz. The other circuit parameters are chosen the same as those used in the calculation of Figs. 1(b) and 1(c).
. The amplitudes of the pumping pulses are chosen as ΔΦa/b/c/Φ0 = 1.4/2.0/1.4% such that the homogeneous coupling strength gT/2π = ga/2π = gb/2π = gc/2π = 20 MHz is induced. The decay rate is chosen as κ/2π = 250 kHz. The other circuit parameters are chosen the same as those used in the calculation of Figs. 1(b) and 1(c).
A quantitative measure of chiral photon flow
We further consider how to describe the chiral pattern of the photon flow. In Fig. 2 as well as in Refs. 11 and 12, the dynamics of perfect chiral flow and perfect non-chiral flow have been investigated. Meanwhile, in more general cases the chiral character which is not perfect but does exist becomes fogged. To characterize how “chiral” the photon flow is, in the following we introduce a quantitative method. As shown in Fig. 3, we assign three unit vectors to the three TLRs,  for the TLR 1,
for the TLR 1,  for the TLR 2 and
for the TLR 2 and  for the TLR 3. We then represent the photon distribution on the necklace by the photon position vector
for the TLR 3. We then represent the photon distribution on the necklace by the photon position vector  where
where  is the photon number population in the TLR j for j = 1, 2, 3. The initial condition used in Fig. 2 corresponds to the initial position
is the photon number population in the TLR j for j = 1, 2, 3. The initial condition used in Fig. 2 corresponds to the initial position  and the state evolution can be expressed by the motion of
and the state evolution can be expressed by the motion of  on the two dimensional plane. The traces of
on the two dimensional plane. The traces of  for some typical values of θΣ and κ are shown in Figs. 4(a) and 4(b). While the 6th panel of Fig. 4(a) indicates the perfect chiral flow in the situation θΣ = π/2 and κ = 0, the other traces become chaotic and irrational as θΣ departs from π/2 and the influence of decoherence is taken into account.
for some typical values of θΣ and κ are shown in Figs. 4(a) and 4(b). While the 6th panel of Fig. 4(a) indicates the perfect chiral flow in the situation θΣ = π/2 and κ = 0, the other traces become chaotic and irrational as θΣ departs from π/2 and the influence of decoherence is taken into account.
Photon position vector  and the chiral area S.
and the chiral area S.
The unit vectors  ,
,  and
and  are assigned to the modes 1, 2 and 3 of the necklace, respectively. The photon position vector is defined as
are assigned to the modes 1, 2 and 3 of the necklace, respectively. The photon position vector is defined as  with
with  and its evolution trace is represented by the dashed line. The chiral area
and its evolution trace is represented by the dashed line. The chiral area  is the directed area swept by
is the directed area swept by  and can be used to characterize the chiral property of the photon flow.
and can be used to characterize the chiral property of the photon flow.
(a),(b) Evolution traces of  at different θΣ with/without the presence of decoherence. (a) depicts the traces in the dissipationless situation κ/2π = 0 and (b) corresponds to κ/2π = 150 kHz. The panels 1–6 in (a) and (b) correspond to θΣ = π/6, π/4, π/3, 5π/12, 17π/36 and π/2, respectively. (c) Chiral area S versus θΣ in the presence of decoherence. The total time T is set as T = 1 μs and the solid, dotted, dot-dashed and dashed lines correspond to the situations with decay rates κ/2π = 0, 100, 200 and 500 kHz, respectively.
at different θΣ with/without the presence of decoherence. (a) depicts the traces in the dissipationless situation κ/2π = 0 and (b) corresponds to κ/2π = 150 kHz. The panels 1–6 in (a) and (b) correspond to θΣ = π/6, π/4, π/3, 5π/12, 17π/36 and π/2, respectively. (c) Chiral area S versus θΣ in the presence of decoherence. The total time T is set as T = 1 μs and the solid, dotted, dot-dashed and dashed lines correspond to the situations with decay rates κ/2π = 0, 100, 200 and 500 kHz, respectively.
To grasp the chiral character from the complicated traces of the photon position vector, our idea is to sum up the area swept by  in a given time, as shown in Fig. 3. We define the chiral area as
in a given time, as shown in Fig. 3. We define the chiral area as

where T is a time scale sufficiently longer than 1/gT but significantly smaller than 1/κ. S has the following properties which make it a suitable measure of the chiral character:
-
1
S is directed. A clockwise trace and its counterclockwise correspondence (e. g. the θΣ = π/2 and 3π/2 situations shown in Fig. 2) result in chiral areas with opposite signs. Therefore, the sign of S can be used to represent the direction of the chiral flow.
-
2
In the perfect non-chiral case θΣ = π shown in the middle panel of Fig. 2, the photon transfers symmetrically to the TLR 2 and TLR 3. Therefore, the trace of
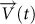 is always along the direction of
is always along the direction of  and zero chiral area is obtained, i. e. S = 0 for θΣ = π.
and zero chiral area is obtained, i. e. S = 0 for θΣ = π. -
3
Obviously, S achieves its maximal value when the photon flow is perfect chiral. Moreover, a faster rotation of
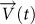 (which means larger gT) and a longer
(which means larger gT) and a longer  (which means more photons involved) lead certainly to a bigger S. From this point of view, S can also be used to demonstrate the influence of driving and dissipation on the chiral photon flow.
(which means more photons involved) lead certainly to a bigger S. From this point of view, S can also be used to demonstrate the influence of driving and dissipation on the chiral photon flow.
The chiral area concept can help us to go beyond the qualitative description of the state evolution in special cases and move into a quantitative and general level of investigation. Despite the complicated evolution  might undergo, the chiral area presents an intuitive and physical description of the chiral character. With this definition we calculate the chiral area versus the θΣ and κ and show our results in Fig. 4(c). It can be seen that the chiral area S decreases rapidly as the total phase θΣ departs from π/2. This is in agreement with our observation of the vector traces shown in Figs. 4(a) and 4(b). Our calculation indicates that the θΣ window suitable for the observation of chiral photon flow is not wide. Meanwhile, the width of this window is barely influenced by the decay rate κ.
might undergo, the chiral area presents an intuitive and physical description of the chiral character. With this definition we calculate the chiral area versus the θΣ and κ and show our results in Fig. 4(c). It can be seen that the chiral area S decreases rapidly as the total phase θΣ departs from π/2. This is in agreement with our observation of the vector traces shown in Figs. 4(a) and 4(b). Our calculation indicates that the θΣ window suitable for the observation of chiral photon flow is not wide. Meanwhile, the width of this window is barely influenced by the decay rate κ.
Discussion
The implementation of the Abelian gauge field in the three-TLR necklace can be regarded as a minimal model. Through a variety of generalizations, the proposed dynamic approach can be used to construct a scalable and flexible quantum simulator of gauge theories. First of all, we consider the scalability of this method, i. e. how to synthesize a gauge field on a circuit QED lattice using this dynamic approach. We take the construction of a square lattice as an example. As shown in Fig. 1(d), we can build a two-dimensional square TLR lattice by four kinds of TLRs with eigenfrequencies ω1/2π = 8 GHz, ω2/2π = 9 GHz, ω3/2π = 10 GHz and ω4/2π = 11 GHz placed in an interlaced form and connected to the ground by the grounding SQUIDs. We assume that the small capacitance/inductance conditions in Eqs. (11) and (12) still hold. To introduce effective passive photon hopping with nontrivial hopping phases, we add extra two-tone a. c. flux driving with frequencies 1 GHz and 3 GHz and appropriate initial phases to the loops of the grounding SQUIDs. In this situation, the cross-talk between next-nearest-neighbor TLRs can be neglected because the corresponding frequency (2 GHz) is far off-resonant with the a. c. flux pumping. Moreover, we can introduce off-diagonal disorder41,42 (i. e. random magnetic fields) into the lattice through randomization of the initial phases of the a. c. driving pulses. While the simulation of diagonal disorder has been realized in ultracold atoms43 and in optical fiber systems45, the simulation of off-diagonal disorder of bosonic particles has also attracted research interest in recent years44. We can also introduce the effective photon-photon interaction to the non-interacting system described in this manuscript by the JCH method, i. e. we couple the TLRs to superconducting qubits resonantly. Though the resonant coupling, the photons are dressed by the qubits and inherit the nonlinearity of the qubits24,25. From the above points of view, we can expect that this dynamic modulation approach may pave a new way of investigating the novel physics of the competition between artificial gauge fields, diagonal and off-diagonal disorder and Hubbard repulsion in the circuit QED system.
In summary, we have investigated the implementation of artificial gauge fields in the circuit QED system by the method of dynamic modulation. We have numerically simulated the photon chiral flow in a three-TLR necklace, discussed the feasibility of observing this phenomenon and proposed a quantitative measure of the chiral character. Our work may offer new perspectives to future studies of quantum simulation and parametric quantum optical physics in SQUID-embedded circuit QED systems.
Methods
Quantization of the TLR necklace
The Lagrangian of the system can be written as:

where Vn (x, t) describes the voltage distribution on the nth TLR for n = 1, 2, 3,  is the corresponding node flux distribution and Vα/φα are the voltage/node flux at locations of the SQUID α for α = a, b, c. In deriving Eq. (19), we have linearized the grounding SQUIDs as
is the corresponding node flux distribution and Vα/φα are the voltage/node flux at locations of the SQUID α for α = a, b, c. In deriving Eq. (19), we have linearized the grounding SQUIDs as  . This assumption is valid because φα(t) ≈ 0. Following the Euler-Lagrangian equation, we get the equation of motion of the node flux in the bulk of the TLRs
. This assumption is valid because φα(t) ≈ 0. Following the Euler-Lagrangian equation, we get the equation of motion of the node flux in the bulk of the TLRs

with  . At the edges of TLRs, based on Kirchhoff's law we get the following boundary conditions
. At the edges of TLRs, based on Kirchhoff's law we get the following boundary conditions






where xa = L1, xb = L1 + L2, xc = 0 and  are the locations of the grounding SQUIDs (the cyclic boundary condition is applied as shown in Eq. (21)). Here without loss of generality we assume the three SQUIDs have the same effective inductance LJ and capacitance CJ. The eigenmodes of the necklace can be obtained by the method of separation of variables. We set φn(x, t) = fn(x)g(t) with
are the locations of the grounding SQUIDs (the cyclic boundary condition is applied as shown in Eq. (21)). Here without loss of generality we assume the three SQUIDs have the same effective inductance LJ and capacitance CJ. The eigenmodes of the necklace can be obtained by the method of separation of variables. We set φn(x, t) = fn(x)g(t) with

where An/θn are the normalized amplitude/phase of the eigenmode in the nth TLR and k is the wave vector. Substituting Eq. (27) to Eqs. (21)–(26) we get the following transcendental equations




When the phases and the wave vector are obtained, the amplitude distribution of the eigenmode in the three TLRs can be further determined by


and the mode normalization conditions. Then we can write the flux distribution of the necklace as a superposition of the eigenmodes  where fn,m(x) corresponds to the mth solution of Eqs. (28)–(31).
where fn,m(x) corresponds to the mth solution of Eqs. (28)–(31).
Due to the of the orthonormality of fn,m(x), the Lagrangian  can be further simplified as
can be further simplified as

where ωm is the eigenfrequency of the mth eigenmode determined by Eqs. (28)–(31). The corresponding Hamiltonian is

with annihilation and creation operators


where  is the canonical momentum of gm. When only the lowest three eigenmodes are taken into consideration, Eq. (13) is reproduced from Eq. (35).
is the canonical momentum of gm. When only the lowest three eigenmodes are taken into consideration, Eq. (13) is reproduced from Eq. (35).
The parametric coupling Hamiltonian
For the grounding SQUID α, the introduction of an extra a. c. flux driving δΦa(t) resulting an additional inter-mode coupling which can be described by Ref. 35

with  for m = 1, 2, 3. Since the 3rd eigenmode is highly localized in the TLR 3, we have
for m = 1, 2, 3. Since the 3rd eigenmode is highly localized in the TLR 3, we have  ,
,  and consequently neglect all
and consequently neglect all  terms in
terms in  . Based on Eq. (6), we set δΦa(t) = ΔΦa cos[(ω1 − ω2)t − θa] to induce the photon conversion between modes 1 and 2. Omitting the counter-rotating terms, we simplify Eq. (38) as
. Based on Eq. (6), we set δΦa(t) = ΔΦa cos[(ω1 − ω2)t − θa] to induce the photon conversion between modes 1 and 2. Omitting the counter-rotating terms, we simplify Eq. (38) as

with  . Notice that when the driving frequency ω1 − ω2 is comparable with the SQUID plasma frequency
. Notice that when the driving frequency ω1 − ω2 is comparable with the SQUID plasma frequency  , the device can not be considered as a passive element because complex quasi-particle excitation behavior will emerge. Meanwhile, with parameters chosen in this manuscript, we can verify that
, the device can not be considered as a passive element because complex quasi-particle excitation behavior will emerge. Meanwhile, with parameters chosen in this manuscript, we can verify that  is satisfied.
is satisfied.
References
Blais, A., Huang, R. S., Wallraff, A., Girvin, S. M. & Schoelkopf, R. J. Cavity quantum electrodynamics for superconducting electrical circuits: An architecture for quantum computation. Phys. Rev. A 69, 062320 (2004).
Wallraff, A. et al. Strong coupling of a single photon to a superconducting qubit using circuit quantum electrodynamics. Nature 431, 162–167 (2004).
Chiorescu, I. et al. Coherent dynamics of a flux qubit coupled to a harmonic oscillator. Nature 431, 159–162 (2004).
You, J. Q. & Nori, F. Atomic physics and quantum optics using superconducting circuits. Nature 474, 589–597 (2011).
Raimond, J. M., Brune, M. & Haroche, S. Manipulating quantum entanglement with atoms and photons in a cavity. Rev. Mod. Phys. 73, 565 (2001).
Wu, Y. & Yang, X. Algebraic method for solving a class of coupled-channel cavity QED models. Phys. Rev. A 63, 043816 (2001).
Mooij, J. E. et al. Josephson Persistent-Current Qubit. Science 285, 1036–1039 (1999).
Martinis, J. M., Nam, S., Aumentado, J. & Urbina, C. Rabi Oscillations in a Large Josephson-Junction Qubit. Phys. Rev. Lett. 89, 117901 (2002).
Koch, J. et al. Charge-insensitive qubit design derived from the Cooper pair box. Phys. Rev. A 76, 042319 (2007).
Schreier, J. A. et al. Suppressing charge noise decoherence in superconducting charge qubits. Phys. Rev. B 77, 180502 (2008).
Nunnenkamp, A., Koch, J. & Girvin, S. M. Synthetic gauge fields and homodyne transmission in Jaynes-Cummings lattices. New. J. Phys 13, 095008 (2011).
Koch, J., Houck, A. A., Hur, K. L. & Girvin, S. M. Time-reversal-symmetry breaking in circuit-QED-based photon lattices. Phys. Rev. A 82, 043811 (2010).
Cho, J., Angelakis, D. G. & Bose, S. Fractional Quantum Hall State in Coupled Cavities. Phys. Rev. Lett. 101, 246809 (2008).
Yang, W. L. et al. Quantum simulation of an artificial Abelian gauge field using nitrogen-vacancy-center ensembles coupled to superconducting resonators. Phys. Rev. A 86, 012307 (2012).
Schmidt, S. & Koch, J. Circuit QED lattices: Towards quantum simulation with superconducting circuits. Annalen der Physik 525, 395 (2013).
Houck, A. A., Türeci, H. E. & Koch, J. On-chip quantum simulation with superconducting circuits. Nature Phys. 8, 292–299 (2012).
Jaksch, D. & Zoller, P. Creation of effective magnetic fields in optical lattices: the Hofstadter butterfly for cold neutral atoms. New J. Phys. 5, 56 (2003).
Galitski, V. & Spielman, I. B. Spin-orbit coupling in quantum gases. Nature 494, 49–54 (2013).
Dalibard, J., Gerbier, F., Juzeliūnas, G. & Öhberg, P. Colloquium: Artificial gauge potentials for neutral atoms. Rev. Mod. Phys. 83, 1523 (2011).
Wang, Z., Chong, Y. D., Joannopoulos, J. D. & Soljačic̀, M. Observation of unidirectional backscattering-immune topological electromagnetic states. Nature 461, 772–775 (2009).
Hartmann, M. J., Brandão, F. G. S. L. & Plenio, M. B. Strongly interacting polaritons in coupled arrays of cavities. Nature Physics 2, 849–855 (2006).
Hu, Y., Ge, G. Q., Chen, S., Yang, X. F. & Chen, Y. L. Cross-Kerr-effect induced by coupled Josephson qubits in circuit quantum electrodynamics. Phys. Rev. A 84, 012329 (2011).
Rebić, S., Twamley, J. & Milburn, G. J. Giant Kerr Nonlinearities in Circuit Quantum Electrodynamics. Phys. Rev. Lett. 103, 150503 (2009).
Lang, C. et al. Observation of Resonant Photon Blockade at Microwave Frequencies Using Correlation Function Measurements. Phys. Rev. Lett. 106, 243601 (2011).
Greentree, A. D., Tahan, C., Cole, J. H. & Hollenberg, L. C. L. Quantum phase transitions of light. Nature Physics 2, 856–861 (2006).
Leib, M., Deppe, F., Marx, A., Gross, R. & Hartmann, M. J. Networks of nonlinear superconducting transmission line resonators. New J. Phys. 14, 075024 (2012).
Jin, J. S., Rossini, D., Fazio, R., Leib, M. & Hartmann, M. J. Photon Solid Phases in Driven Arrays of Nonlinearly Coupled Cavities. Phys. Rev. Lett. 110, 163605 (2013).
Bourassa, J., Beaudoin, F., Gambetta, J. M. & Blais, A. Josephson-junction-embedded transmission-line resonators: From Kerr medium to in-line transmon. Phys. Rev. A 86, 013814 (2012).
Umucalilar, R. O. & Carusotto, I. Fractional Quantum Hall States of Photons in an Array of Dissipative Coupled Cavities. Phys. Rev. Lett. 108, 206809 (2012).
Hayward, A. L. C., Martin, A. M. & Greentree, A. D. Fractional Quantum Hall Physics in Jaynes-Cummings-Hubbard Lattices. Phys. Rev. Lett. 108, 223602 (2012).
Bardyn, C. E. & Imamoğlu, A. Majorana-like Modes of Light in a One-Dimensional Array of Nonlinear Cavities. Phys. Rev. Lett. 109, 253606 (2012).
Leib, M. & Hartmann, M. J. Many body physics with coupled transmission line resonators. Physica Scripta T153, 014042 (2013).
Peropadre, B. et al. Tunable coupling engineering between superconducting resonators: From sidebands to effective gauge fields. Phys. Rev. B. 87, 134504 (2013).
Z-Bajjani, E. et al. Quantum superposition of a single microwave photon in two different ‘colour’ states. Nature Physics 7, 599–603 (2011).
Felicetti, S. et al. Dynamical Casimir Effect Entangles Artificial Atoms. Phys. Rev. Lett. 113, 093602 (2014).
Frunzio, L., Wallraff, A., Schuster, D. I., Majer, J. & Schoelkopf, R. J. Fabrication and characterization of superconducting circuit QED devices for quantum computation. IEEE Trans. Appl. Supercond. 15, 860 (2005).
Sillanpää, M. A., Park, J. I. & Simmonds, R. W. Coherent quantum state storage and transfer between two phase qubits via a resonant cavity. Nature 449, 438–442 (2007).
Wang, H. et al. Deterministic Entanglement of Photons in Two Superconducting Microwave Resonators. Phys. Rev. Lett. 106, 060401 (2011).
Fang, K. J., Yu, Z. F. & Fan, S. H. Realizing effective magnetic field for photons by controlling the phase of dynamic modulation. Nature photonics 6, 782–787 (2012).
Mariantoni, M. et al. Planck Spectroscopy and Quantum Noise of Microwave Beam Splitters. Phys. Rev. Lett. 105, 133601 (2010).
Altland, A. & Simons, B. D. Field theory of the random flux model. Nucl Phys B 562, 445–476 (1999).
Xie, X. C., Wang, X. R. & Liu, D. Z. Kosterlitz-Thouless-Type Metal-Insulator Transition of a 2D Electron Gas in a Random Magnetic Field. Phys. Rev. Lett. 80, 3563 (1998).
Sanchez-Palencia, L. & Lewenstein, M. Disordered quantum gases under control. Nature Physics 6, 87–95 (2010).
Edmonds, M. J. et al. From Anderson to anomalous localization in cold atomic gases with effective spin-orbit coupling. New J. Phys. 14, 073056 (2012).
Lahini, Y. et al. Anderson Localization and Nonlinearity in One-Dimensional Disordered Photonic Lattices. Phys. Rev. Lett. 100, 013906 (2008).
Acknowledgements
Y.P.W. would like to acknowledge useful discussions with Xin-You Lü. The work was supported in part by the National Fundamental Research Program of China (Grants No. 2012CB922103 and No. 2013CB921804), the National Nature Science Foundation of China (Grants No. 11104096, No. 11374117, No. 11274351, No. 11375067 and No. 11275074) and the PCSIRT (No. IRT1243). Y.H. is supported by the fellowship of Hong Kong Scholars Program (Grant No. 2012-80).
Author information
Authors and Affiliations
Contributions
Y.H. proposed the idea. Y.P.W. carried out all calculations under the guidance of Y.H. W.W., Z.Y.X., W.L.Y. and Y.W. participated in the discussions. Y.P.W., Y.H. and Z.Y.X. contributed to the interpretation of the work and the writing of the manuscript.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Rights and permissions
This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivs 4.0 International License. The images or other third party material in this article are included in the article's Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder in order to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-nd/4.0/
About this article
Cite this article
Wang, YP., Wang, W., Xue, ZY. et al. Realizing and characterizing chiral photon flow in a circuit quantum electrodynamics necklace. Sci Rep 5, 8352 (2015). https://doi.org/10.1038/srep08352
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep08352
This article is cited by
-
Realizing universal quantum gates with topological bases in quantum-simulated superconducting chains
npj Quantum Information (2017)
-
Ultrafast quantum computation in ultrastrongly coupled circuit QED systems
Scientific Reports (2017)
-
Detecting topological phases of microwave photons in a circuit quantum electrodynamics lattice
npj Quantum Information (2016)
-
Pseudo-time-reversal symmetry and topological edge states in two-dimensional acoustic crystals
Scientific Reports (2016)
-
Quantum state transfer and controlled-phase gate on one-dimensional superconducting resonators assisted by a quantum bus
Scientific Reports (2016)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.






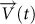 is always along the direction of
is always along the direction of  and zero chiral area is obtained, i. e. S = 0 for θΣ = π.
and zero chiral area is obtained, i. e. S = 0 for θΣ = π.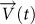 (which means larger gT) and a longer
(which means larger gT) and a longer  (which means more photons involved) lead certainly to a bigger S. From this point of view, S can also be used to demonstrate the influence of driving and dissipation on the chiral photon flow.
(which means more photons involved) lead certainly to a bigger S. From this point of view, S can also be used to demonstrate the influence of driving and dissipation on the chiral photon flow.