Abstract
Understanding the elastic response on the nanoscale phase boundaries of multiferroics is an essential issue in order to explain their exotic behaviour. Mixed-phase BiFeO3 films, epitaxially grown on LaAlO3 (001) substrates, have been investigated by means of scanning probe microscopy to characterize the elastic and piezoelectric responses in the mixed-phase region of rhombohedral-like monoclinic (MI) and tilted tetragonal-like monoclinic (MII,tilt) phases. Ultrasonic force microscopy reveal that the regions with low/high stiffness values topologically coincide with the MI/MII,tilt phases. X-ray diffraction strain analysis confirms that the MI phase is more compliant than the MII,tilt one. Significantly, the correlation between elastic modulation and piezoresponse across the mixed-phase regions manifests that the flexoelectric effect results in the enhancement of the piezoresponse at the phase boundaries and in the MI regions. This accounts for the giant electromechanical effect in strained mixed-phase BiFeO3 films.
Similar content being viewed by others
Introduction
In the race for the development of sensing and actuation applications, a lot of attention has been paid to the search for materials with large mechanical response via external stimuli, such as piezoelectrics and shape memory alloys1. These materials present a complexity of phase constitutions and the transformation between different phases plays a crucial role in showing large electromechanical responses2. Perovskite BiFeO3 (BFO) is found to be a green piezo/ferroelectric material with longitudinal piezoelectric coefficient3 (d33) larger than 60 pm/V and spontaneous ferroelectric polarization4 of about 100 μC/cm2. Therefore, BFO has been considered as a good candidate to replace current Pb-based piezoelectrics.
Via imposing epitaxial strain to BFO films, the ground phase can be tuned from rhombohedral (R) to tetragonal (T) or orthorhombic, depending on the degree of strain and its sign (compressive or tensile)5,6,7. Furthermore, by employing suitable substrates and thickness values, the R-like monoclinic MI and T-like monoclinic MII phases can coexist to form nanoscale self-organized alternative stripes8. These self-organized phase boundaries provide a superior template to understand the fundamental physics underlying the giant electromechanical responses. Recently, researchers have thus spent a lot of efforts making relevant progresses. Some studies, carried out with techniques such as atomic force microscopy (AFM), X-ray diffraction (XRD) and transmission electron microscopy (TEM), suggest that the giant piezoelectric response in mixed-phase BFO films can be attributed to a phase transformation from MII to mixed MI-MII8,9,10. The phase boundaries in mixed-phase BFO films show an extraordinary enhancement of their piezoelectric response, e.g., a remarkably high d33 (~ 400 pm/V)11. Such a superior piezoelectric response can be possibly associated with the flexoelectric effect. In addition to its superior piezoelectric response, intriguing magnetism properties have been also found12. Their origins can be attributed to either piezomagnetic or flexomagnetic effects11. The flexoelectric effect is the polarization response of materials to a strain gradient (∂u/∂x), i.e., an inhomogeneous deformation due to a break in centro-symmetry. The bulk electromechanical polarization (P) can be described with the following equation:

On the right hand side of Eq. (1), the first term is the dielectric response with the dielectric susceptibility χ and the second term is the flexoelectric response with the flexoelectric coefficient μ. Flexoelectricity is of great interest for the development of nanoscale technologies, because large strain variations often present on the nanoscale to produce a strong flexoelectric effect13.
Most of these studies are based on structural or electrical and magnetic properties. However it is also very important to understand the elastic modulation of these phase boundaries, which could help to individuate the direct causes for large flexoelectricity in BFO. Studying the elastic moduli of nanometric mixed-phase regions in sub-100 nm-thick BFO films is a severe challenge for conventional techniques (such as Nanoindentation), because they do not provide sufficient spatial resolution. AFM possesses the required resolution to characterize local elastic properties of compliant materials such as polymers. However, the cantilevers employed in AFM are relatively too compliant (typically the spring constant is well under 100 N/m) to distinguish the elastic difference of very stiff materials, e.g., semiconductors and metal oxides. Ultrasonic force microscopy (UFM) is an offspring of AFM specifically developed to measure the local elastic properties of stiff materials with compliant cantilevers14,15,16. UFM operates by detecting the intrinsic nonlinearity of the probe-sample interaction, thanks to the application of a vertical vibration to the sample at an ultrasonic frequency (i.e., the exciting frequency is much higher than the fundamental resonant frequency of the cantilever and off higher resonances).
In this paper, the topography, stiffness and piezoresponse of mixed-phase BFO are investigated by scanning probe techniques, i.e., AFM, UFM and piezoresponse force microscopy (PFM). It is demonstrated that UFM can qualitatively investigate the elastic modulation inside the mixed-phase regions of BFO thin films. Unlike the stiffer pure R-phase BFO, the stiffness of the R-like MI phase is found to be lower than that of the T-like MII phase. XRD strain analysis by means of reciprocal space mapping (RSM) has been also carried out. The RSM results are in good agreement with the UFM findings. The elastic modulus exhibits kinks at the phase boundaries and higher elastic gradient in the MI phase. The correlation between the elastic modulation and piezoresponse in mixed-phase regions indicates that the flexoelectric effect causes the piezoresponse peaks at the phase boundaries and a higher piezoresponse inside the MI regions compared to that inside the MII and tilted T-like monoclinic MII,tilt regions.
Results
Scanning probe characterizations
The topography (AFM), the elastic response (UFM) and out-of-plane (OP) piezoresponse of the same area are shown in Fig. 1. Topography can be acquired simultaneously to either UFM or PFM images. In this case, we only report one AFM image, as they are identical. The topographic image shows the atomic flat terraces of MII matrix and the mixed-phase regions. The mixed phase regions consist of the MI and MII,tilt phases12. The MI and MII,tilt phases can be considered as intermediate phases making it possible a continuous transition from the highly-strained MII phase to the highly-relaxed distorted R phase with increasing film thickness. The UFM image shows a clear contrast in the mixed-phase regions (Fig. 1b), indicating that UFM can resolve the elastic properties of the stripes on the nanoscale. A well detectable elastic modulation is noticeable across these regions, i.e., the stiffness is not uniform. Curved loops of the OP-PFM image belong to the MI/MII,tilt phase boundaries and each MI phase region is enclosed by a loop (Fig. 1c)12,17. On the other hand, the elastic modulation well correlates with the topographic and piezoresponse features.
To better illustrate the correlations among topography, stiffness and piezoelectricity in the mixed-phase regions, the line profile at the mixed-phase regions of the AFM image and the corresponding profiles of UFM and PFM are shown in Fig. 2. The mixed-phase regions exhibit an asymmetric peak-and-valley landscape (Fig. 2a), where the tilted angles of left and right sides of the peaks are 2.6° and 1.6°, respectively8,12. The left/right sides of a peak are the areas of the MI/MII,tilt phases with widths of approximately 35 and 80 nm, respectively. These peaks and valleys are exactly the phase boundaries between the MI and MII,tilt phases. From the stiffness profile (Fig. 2b), the low/high stiffness values topologically coincide with the MI/MII,tilt phases, indicating that the MI phase has an elastic modulus lower than that of MII,tilt phase.
Profiles of topography (a), stiffness (b) and piezoresponse (c) along the lines across the same mixed-phase regions drawn in Fig. 1.
The shadowed areas indicate the MI phase and the others the MII,tilt phase. The arrows in (b) indicate the kinks of the elastic modulation at the boundaries.
Both experimental and theoretical studies demonstrate that the elastic modulus of the strain-free R phase (from 130 to 200 GPa, depending on the direction of interest) is higher than that of the highly-strain MII phase (~100 GPa)18,19,20. Calculations by means of first-principles density-function theory (DFT) also confirm that BFO with a lower unit-cell volume has a higher elastic modulus. Based on the TEM results, the average lattice parameters of the MI phase can be still estimated as a = b ≈ 3.82 Å, c ≈ 4.16 Å in a pseudo-tetragonal form, significantly different from that of the R phase (a = b ≈ 3.92 Å, c ≈ 4.01 Å). These observations indicate that the MI phase has the smallest unit-cell volume (12.14 Å3 per atom) compared to the other phases (13.28 Å3 per atom for the MII phase and 12.32 Å3 per atom for the R phase). Thus, the MI phase should be the toughest one according to this supposition. Nevertheless, the UFM data in terms of the stiffness in the mixed-phase regions are against the DFT prediction.
X-ray diffraction strain analysis
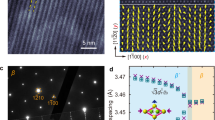
To verify the UFM findings, room-temperature RSM has been then performed. RSM data of the partially-relaxed BFO thin film on LaAlO3 (001) substrate (LAO) include the diffraction peaks of the MI, MII and MII,tilt phases (Fig. 3). The MI phase has a lattice constant in c axis of 4.16 Å, whereas MII and MII,tilt phases have an identical lattice constant (c = 4.65 Å). Both the MI and MII,tilt phases have an off-normal c-axis orientation, where the MI phase has a tilted angle of 2.8° and the MII,tilt phase of 1.6°. The tilted angle values are well consistent with the results obtained from the AFM topography. Fig. 4 shows the diffraction profiles across the MII,tilt peaks in Qx and Qz and the MI peak in the longitudinal direction. The peaks can be fitted by Gaussian functions; the full widths at half maximum (FWHM) of those peaks are listed in Table I. The FWHM of the MI peak in Qx/Qz is the x/z component of the FWHM in the longitudinal direction. Obviously, the peak of the MI phase is wider than that of the MII,tilt phase by 58% in Qx and 33% in Qz. The wider peak in the Qx reflects the misorientation of the c axis, while the wider peak in the Qz reflects a larger distortion in the c-axis spacing and/or a smaller grain size in the c axis. From the cross-section TEM image, reported in the supplementary materials by Liu et al.8, the MI and MII,tilt phases have a well epitaxial relationship with the MII phase and the substrate. The grains of all phases extend from the surface to the substrate, so those phases have the same grain size along the out-of-plane direction. Therefore, the broadness in Qz of MI phase is merely attributed to the distortion of the c-axis spacing instead of a grain size effect. The larger misorientation and spacing distortion of the c-axis of the MI phase depict its more ambiguous lattice structure, which implies that the stiffness in the MI phase is lower than that in MII,tilt.
XRD Peak profiles of (a) the MII (blue) and MII,tilt (olive) phases in Qx, (b) the MII,tilt phase in Qz and (c) the MI phase in the longitudinal direction.
The peak of the MII phase can be deconvoluted into two components of crystalline and diffusive scatterings due to the fact that the film thickness is of only 70 nm.
Furthermore, the lower value in stiffness of the MI phase can be evidenced from the structural aspect. In the mixed region, the MI and MII,tilt phases are the products of the strain relaxation and the intermediate phases to connect with the MII and R phases. The MII,tilt phase has the same structure of the MII phase but slightly tilted with respect to the surface normal. The MI phase has a large tilted angle and the smallest lattice structure. For compensating the difference of height between the MII and R phases, MI varies more dramatically (a transverse distance of about 35 nm with a tilted angle of 2.8° on the macroscale) than MII,tilt (a transverse distance of about 80 nm with a tilted angle of 1.6° on the macroscale), implying that MI is softer than MII,tilt. Therefore, we suggest that the intermediate MI phase is not in the low energy state and not so rigid and stable as the R and MII phases, thus being more compliant than the other phases.
Flexoelectric effect
The correlation between the stiffness and piezoresponse profiles (Fig. 2b and 2c) can illustrate the flexoelectric effect in mixed-phase BFO films. From the stiffness profile, Kinks at the interface indicate a strain discontinuity between MI and MII,tilt phases. Those kinks coincide with the piezoelectric peaks at the boundaries, which implies that the flexoelectric effect results in the enhancement of piezoresponse. In addition, the slope of stiffness on the MI side is higher than that on the MII,tilt side, indicating that the elastic (strain) gradient in the MI phase is higher than that in the MII,tilt phase. Besides the piezoresponse inside the more compliant MI regions is higher than that inside the neighboring stiffer MII,tilt and matrix MII regions. Therefore, the higher piezoresponse in the MI regions can be attributed to the flexoelectric effect induced by the strain gradient. This result of higher piezoeresponse in MI regions conflicts with the general understanding that the piezoelectricity of MII phase is a higher than that of R phase21. It is because MI phase is not a low energy state as other phases and behaves differently from the ground R phase in piezoelectricity.
To estimate the strain magnitude in the mixed-phase MI phase near the MI and MII,tilt interface, a θ-2θ scan with respect to the surface normal of the MI phase (Fig. 5a) is extracted from the RSM image (Fig. 3) at H = 0.041 r.l.u. It shows an asymmetric diffraction peak, indicating that the lattice constant c is not uniform in MI phase. The peak is fitted by an asymmetric Gaussian function and the half widths at half maximum are σh = 6.63×10−3 r.l.u. on the high Qz side and σl = 7.89×10−3 r.l.u. on the low Qz side. σh presents the contributions of the normal distribution of lattice constant and the grain-size broadening. The larger σl indicates there is an additional component (σsg) due to strain gradient at phase boundaries. Assuming a combination of peak widths by  , σsg = 4.29×10−3 r.l.u. is obtained, corresponding to a strain of +0.47%. There is a strain in the compliant MI phase at the boundary. To accommodate the lattice mismatch between MI and MII,tilt phases (Fig. 5b), the more compliant MI phase exhibits an expansion of the out-of-plane lattice constant by , whereas become its maximum at the interface. The strain relaxes with the distance apart from the phase boundary. Such a strain gradient supports the findings by UFM and PFM that the flexoeletric effect accounts for the extraordinary polarization in mixed-phase BFO thin films. The enhancement of polarization in the mixed-phase regions is about 55 μC/cm2 from Ref. 22, the region with strain gradient is 17 nm in width (half width of MI regions) and the volume fraction of the MI phase is 50% according to topography. Therefore the flexoelectric coefficient of the MI phase is estimated to be ≈ 1.4 μC/m by Eq. (1), which is comparable to that of perovskite ceramics in paraelectric phases13.
, σsg = 4.29×10−3 r.l.u. is obtained, corresponding to a strain of +0.47%. There is a strain in the compliant MI phase at the boundary. To accommodate the lattice mismatch between MI and MII,tilt phases (Fig. 5b), the more compliant MI phase exhibits an expansion of the out-of-plane lattice constant by , whereas become its maximum at the interface. The strain relaxes with the distance apart from the phase boundary. Such a strain gradient supports the findings by UFM and PFM that the flexoeletric effect accounts for the extraordinary polarization in mixed-phase BFO thin films. The enhancement of polarization in the mixed-phase regions is about 55 μC/cm2 from Ref. 22, the region with strain gradient is 17 nm in width (half width of MI regions) and the volume fraction of the MI phase is 50% according to topography. Therefore the flexoelectric coefficient of the MI phase is estimated to be ≈ 1.4 μC/m by Eq. (1), which is comparable to that of perovskite ceramics in paraelectric phases13.
(a) Asymmetric θ-2θ diffraction peak to the surface normal of the MI phase extracted from the RSM image (Fig. 3) at H = 0.041 r.l.u. The peak can be better fitted by an asymmetric Gaussian function (red), while a symmetric Gaussian function (blue) is reported only to visualize the asymmetry of the peak. (b) Schematic illustration of the strain gradient of the MI phase near the interface (yellow line) between the MI (brown) and MII (green) phases.
Discussion
The elastic response in the mixed-phased region of BFO thin films, epitaxially grown on LAO substrates, has been investigated by means of scanning probe microscopy and X-ray diffraction strain analysis. Ultrasonic force microscopy can spatially resolve the nanoscale elastic modulation and regions with low/high stiffness values topologically coincide with the MI/MII,tilt phases. Although the MI phase has a smaller unit-cell volume, it is more compliant than the other phases, as confirmed by X-ray diffraction strain analysis. Because of the flexoelectric effect, the elastic kink at the boundary produces the piezoresponse peak at the phase boundary and a higher elastic gradient on the MI side produces a higher piezoresponse inside the MI phase, resulting in an enhanced electromechanical response in the strained mixed-phase BFO films.
Methods
Mixed-phase BFO films are epitaxially grown on a single-crystal LAO substrate (LAO) by means of pulse laser deposition. The thickness of the samples herein reported is of around 70 nm. These BFO films are subjected to a highly compressive strain (> 4%), thus MI and MII phases coexist.
The AFM setup is made of a commercial probe head (NT-MDT, SMENA) with electronics and control software developed in-house. The cantilevers employed have a diamond-coated tip, a nominal spring constant of around 5.5 N/m and a resonant frequency of around 150 kHz (NT-MDT, DCP-01). To conduct UFM, the samples are mounted on a piezo-disc that can be driven at around 4 MHz with an amplitude modulation frequency of 3.7 kHz (Agilent 33220A) to generate a maximal oscillating amplitude below 1 nm. The piezoresponse of BFO films is characterized by PFM. PFM and UFM can be quickly switched from one to the other while the tip is still in contact. To collect the UFM and PFM data, a digital lock-in amplifier (Zurich, HF2LI) is employed. The color codes of the images are the following: brighter for higher regions in AFM, higher stiffness in UFM and higher piezoelectricity in PFM. For UFM in particular, a brighter color represents a lower local indentation and thus corresponds to a stiffer region.
RSM has been performed using a standard Huber four-circle X-ray diffractometer operated at 50 kV and 200 mA with Cu Kα1 radiation in the X-ray laboratory at National Synchrotron Radiation Research Center (NSRRC) in Hsinchu, Taiwan. The incident beam is monochromated with a flat Ge (111) crystal and two sets of slits serve to eliminate Cu Kα2 so as to obtain a high wave-vector resolution of 0.01 nm-1 order in the reciprocal space. The reciprocal space map is recorded by a series of θ–2θ scans with different ω and plotted in the reciprocal lattice unit Q that is normalized to the LAO (001) substrate (1 r.l.u. = 2π/aLAO).
References
Zhang, J. X. et al. A nanoscale shape memory oxide. Nat. Commun. 4, 3768 (2013).
Fu, H. X. & Cohen, R. E. Polarization rotation mechanism for ultrahigh electromechanical response in single-crystal piezoelectrics. Nature 403, 281 (2000).
Chu, Y.-H. et al. Domain control in multiferroic BiFeO3 through substrate vicinality. Adv. Mater. 19, 2662 (2007).
Chu, Y.-H., Martin, L. W., Holcomb, M. B. & Ramesh, R. Controlling magnetism with multiferroics. Mater. Today 10, 16 (2007).
Christen, H. M., Nam, J. H., Kim, H. S., Hatt, A. J. & Spaldin, N. A. Stress-induced R-MA-MC-T symmetry changes in BiFeO3 films. Phys. Rev. B 83, 144107 (2011).
Yang, J. C. et al. Orthorhombic BiFeO3, Phys. Rev. Lett. 109, 247606 (2012).
Zeches, R. J. et al. A strain-driven morphotropic phase boundary in BiFeO3 . Science 326, 977 (2009).
Liu, H.-J. et al. Strain-driven phase boundaries in BiFeO3 thin films studied by atomic force microscopy and x-ray diffraction. Phys. Rev. B 85, 014104 (2012).
Zhang, J. X. et al. Large field-induced strains in a lead-free piezoelectric material. Nat. Nanotechnol. 6, 98 (2011).
Damodaran, A. R. et al. Nanoscale structure and mechanism for enhanced electromechanical response of highly strained BiFeO3 thin films. Adv. Mater. 23, 3170 (2011).
Zhang, J. X., Zeches, R. J., He, Q., Chu, Y.-H. & Ramesh, R. Nanoscale phase boundaries: a new twist to novel functionalities. Nanoscale 4, 6196 (2012).
He, Q. et al. Electrically controllable spontaneous magnetism in nanoscale mixed phase multiferroics. Nat. Commun. 2, 225 (2011).
Zubko, P., Catalan, G. & Tagantsev, A. K. Flexoelectric effect in solids. Annu. Rev. Mater. Res. 43, 387 (2013).
Kolosov, O. & Yamanaka, K. Nonlinear detection of ultrasonic vibrations in an atomic force microscope. Jpn. J. Appl. Phys. 32, L1095 (1993).
Kolosov, O., Castell, M. R., Marsh, C. D. & Briggs, G. A. D. Imaging the elastic nanostructure of Ge islands by ultrasonic force microscopy. Phys. Rev. Lett. 81, 1046 (1998).
Dinelli, F. et al. Mapping surface elastic properties of stiff and compliant materials on the nanoscale using ultrasonic force microscopy. Phil. Mag. A, 80, 2299 (2000).
Chen, Y.-C. et al. Electrical control of multiferroic orderings in mixed-phase BiFeO3 films. Adv. Mater. 24, 3070 (2012).
Doig, K. I. et al. Coherent magnon and acoustic phonon dynamics in tetragonal and rare-earth-doped BiFeO3 multiferroic thin films. Phys. Rev. B 88, 094425 (2013).
Shang, S. L., Sheng, G., Wang, Y., Chen, L. Q. & Liu, Z. K. Elastic properties of cubic and rhombohedral BiFeO3 from first-principles calculations. Phys. Rev. B 80, 052102 (2009).
Dong, H., Chen, C., Wang, S., Duan, W. & Li, J. Elastic properties of tetragonal BiFeO3 from first-principles calculations. Appl. Phys. Lett. 102, 182905 (2013).
Ederer, C. & Spaldin, N. A. Effect of epitaxial strain on the spontaneous polarization of thin film ferroelectrics. Phys. Rev. Lett. 95, 257601 (2005).
Zhang, J. X. et. al. Microscopic origin of the giant ferroelectric polarization in tetragonal-like BiFeO3 . Phys. Rev. Lett. 107, 147602 (2011).
Acknowledgements
This work is supported by Ministry of Science and Technology of Taiwan (Grant NO. MOST 102-2112-M-029-005-MY3) and National Chiao Tung University (2013 NCTU Short-term Research Program Scholarship). The authors would like to thank Dr. P. Pinque of NEST, Istituto Nanoscienze-CNR and Scuola Normale Superiore for his kindly support.
Author information
Authors and Affiliations
Contributions
C.-E.C., H.-J.L. and F.D. performed the experiments. H.-J.L. and Y.-H.C. contributed material. F.S.-S.C., F.D., Y.-H.C., Y.-C.C. and C.-S.C. conceived and designed the experiments. F.S.-S.C., Y.-H.C. and F.D. co-wrote the paper.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Rights and permissions
This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivs 4.0 International License. The images or other third party material in this article are included in the article's Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder in order to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-nd/4.0/
About this article
Cite this article
Cheng, CE., Liu, HJ., Dinelli, F. et al. Revealing the flexoelectricity in the mixed-phase regions of epitaxial BiFeO3 thin films. Sci Rep 5, 8091 (2015). https://doi.org/10.1038/srep08091
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep08091
This article is cited by
-
Long-range symmetry breaking in embedded ferroelectrics
Nature Materials (2018)
-
Giant linear strain gradient with extremely low elastic energy in a perovskite nanostructure array
Nature Communications (2017)
-
Broadband and wide-angle RCS reduction using a 2-bit coding ultrathin metasurface at terahertz frequencies
Scientific Reports (2016)
-
Giant elastic tunability in strained BiFeO3 near an electrically induced phase transition
Nature Communications (2015)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.