Abstract
In this article, the controllability of asynchronous Boolean multiplex control networks (ABMCNs) with time delay is studied. Firstly, dynamical model of Boolean multiplex control networks is constructed, which is assumed to be under Harvey' asynchronous update and time delay is introduced both in states and controls. By using of semi-tensor product (STP) approach, the logical dynamics is converted into an equivalent algebraic form by obtaining the control-depending network transition matrices of delayed system. Secondly, a necessary and sufficient condition is proved that only control-depending fixed points of the studied dynamics can be controlled with probability one. Thirdly, respectively for two types of controls, the controllability of dynamical control system is investigated. When initial states and time delay are given, formulae are obtained to show a) the reachable set at time s under specified controls; b) the reachable set at time s under arbitrary controls; c) the reachable probabilities to different destination states. Furthermore, an approach is discussed to find a precise control sequence which can steer dynamical system into a specified target with the maximum reachable probability. Examples are shown to illustrate the feasibility of the proposed scheme.
Similar content being viewed by others
Introduction
Boolean networks (BNs), as a class of simplified discrete models, are widely applied to reveal the generic properties of biological systems in an integrative and holistic manner. In 1969, random Boolean networks (RBNs), also known as N-K models, were originally proposed by Stuart Kauffman1. This classic model consists of N nodes representing genes, each of which receives inputs from K randomly selected neighbors. The nodes on networks are characterized by two qualitative values, usually referred to logical 0 and 1, to present the active and repressing states of genes, respectively. Boolean rules assigned to nodes are employed to indicate the mutual regulations among genes. Based on synchronous update, at each time t, the state of each node on network is determined by the Boolean rule and K inputs at the previous time t-1. During the past few decades, Boolean networks have been used to unveil characteristics of complex systems and abundant of results have been achieved, such as dynamical behaviors of BNs2,3, efficient attractor-seeking algorithms4,5,6, biological control7,8 and some applications in biological research9,10,11.
Biological information operates on multiple hierarchical levels of living organization12. From the viewpoint of systems biology, system-level analysis of biological regulation requires the interactions of genes on a holistic level, rather than the characteristics of isolated parts of an organism13. As mentioned in Ref. 14, “the same gene or biochemical species can be involved in a regulatory interaction, in a metabolic reaction, or in another signaling pathway”. Therefore, to understand the intricate variability of biological systems, where many hierarchical levels and interactions coexist, a new level of description is required. Meanwhile, multiplex networks as an extension of complex networks were firstly proposed by Mucha in 201015, which is composed of several layered networks interrelated with each other shown in Fig. 1. Each layer in multiplex networks could have particular features and dynamical processes. Interconnections between layers are represented by some special nodes on behave of different roles participating in multiple layers of interactions. Different from the traditional sense of coupling, the final states of those common nodes at each time step are determined by all of involved layers. During the past four years, a variety of studies based on multiplex networks have been achieved, including network topology and dynamic properties16, diffusion dynamics17,18 and game theory19,20, etc. It's noteworthy that multiplex networks provide a novel way to construct the multilevel models of biochemical systems and be better depict a richer structure of interactions.
To incorporate mutual regulations of genes observed in the real biological system, Boolean networks as abstract models are employed to investigate dynamical properties of systems. For a certain degree of simplification, synchronous update scheme is adopted in the previous studies of RBNs, which is based on an assumption that update scheme isn't an essential factor on the consideration of dynamical behaviors. However, regulated entities can't implement the interactions and renew their states simultaneously at each time step by following a synchronized clock. As the studies in Ref. 21, “factors such as mRNA and protein synthesis, degradation and transport times mean that the system is replete with delays of varying amounts and genes are activated or inhibited in a fundamentally asynchronous manner”, that means there are multiple timescales should be considered in the biological systems. Asynchronous Boolean networks (ABNs) were firstly proposed by Harvey et al.22, followed by a series of related studies. In23, Greil et al. illustrated that the growth of the mean number and size of attractors in asynchronous critical BNs are in strong contrast to the synchronous version. Furthermore, dynamics of critical BNs under deterministic asynchronous update was also studied24; in25, Saadatpour et al. carried out a comparative study on the attractors of a signal transduction network modelled by BNs under synchronous and asynchronous updating schemes; in26, Tournier and Chaves investigated dynamics of the interconnection of two ABNs by directly analyzing the properties of two individual modules, that can be applied to analyze the multicellular modeling and high dimensional model; in27, asynchronous stochastic Boolean networks were proposed to investigate dynamical behaviors of a T-helper network; in28, Jack et al. simulated quantitative cellular responses of signal transduction in a single cell by means of asynchronous threshold BNs. The previous results were presented to verify the asynchronous update is more plausible for many cases of biological systems. Therefore, studies of BNs under asynchronous stochastic update are meaningful and applicable.
From system-level understanding of biological systems, to find a mechanisms that systematically control the states of regulatory entities can be implemented to minimize malfunctions and provide potential therapeutic targets for treatment of disease29,30. Boolean control networks (BCNs) as dynamical control systems provide an efficient approach to carry out theoretical and numerical analysis31. Controllability, roughly speaking, which is to steer a control system from an arbitrary initial state to an arbitrary final state by using the set of admissible controls, is one of the fundamental concepts at the onset of control theory infiltrating into the research of gene regulatory networks (GRNs)32,33. Over the past few years, controllability of BCNs have been receiving considerable attention, such as controllability and observability of BCNs34; controllability of BCNs with time-invariant delay35 and time-variant delay36 as well as time delay involved both in states and controls37; controllability of μ-th order BCNs38 and the approach to transform μ-th order BCNs to equivalent time-variant BCNs39; studies on controllability of BCNs via the Perron-Frobenius theory40, etc. The previous works were based on an independent network, which represents the assembly of genes or other entities to fulfil a specified function. With the in-depth of research, it is necessary to further study how the interplay among multiple interdependent networks affects dynamical behaviors of system. Compared with the traditional models, Boolean multiplex networks have more complex topology structure and higher holistic level which can provide a more generalized model to be better in conformity with the development of biology. Moreover, most of the previous studies on controllability of BCNs were assumed to be updated under synchronous scheme, i.e. the studied models are deterministic systems. As the above discussion, asynchronous update is closer to the real situation, based on which studies on BNs can be more likely to obtain the essential properties of biological systems. In41, the reachable sets of Boolean multiplex networks under asynchronous update scheme at time s were revealed, where the asynchronous scheme was based on randomly chosen update nodes at each time step. However, Due to signal propagation delays in the environment, a propagation delay τ can be seen as a particular form of asynchronous phenomenon existing in the processes of transcription and translation in biological systems42 or information propagation in society systems43. Hence, we think it's valuable to extend the related research into the field of asynchronous Boolean multiplex networks with time delay.
In this article, controllability of ABMCNs with time delay is discussed. The dynamical model of Boolean multiplex control networks is constructed by introducing inputs as controls into the model proposed by Cozzo et al.14. For obtaining the more general results, time delay is involved both in states and inputs44. Harvey's update scheme, i.e. only one node could be randomly chosen to renew its state at each time step, is implemented. In45, as a kind of non-deterministic system, the controllability of probabilistic Boolean networks was discussed, in which the concept of controllable probability was firstly proposed. But, authors just showed the sufficiency of the controllability with probability but not verify the necessary. In our work, a necessary and sufficient condition is proved that only control-depending fixed points of asynchronous delayed system can be controlled with probability one, which provide the theoretical basis to discuss the controllability of non-deterministic system from the perspective of probability. Based on the algebraic representation of the studied model, controllability of delayed system is to be analytically discussed respectively for two types of controls, i.e. free Boolean control sequences and the controls satisfying certain logical rule. When initial state sequence and time delay are given, we discuss the formulae to calculate reachable sets at time s under specified or free controls, as well as the reachable probabilities to different destination states. Furthermore, we are to illustrate the method to determine specific controls which can drive dynamical system to a given target with the maximum reachable probability.
This article is organized as follows. In Preliminaries, semi-tensor product as mathematic tools applied in this article is briefly introduced. In Main Results, the studied model of ABMCNs with time delay is firstly proposed and converted into linear form. Based on two types of controls, the controllability of dynamical control system is discussed. Some examples are shown to illustrate the main results. Finally, a concluding remark is given.
Preliminaries
In this section, STP of matrix is briefly introduced, by means of which logical dynamics can be converted into an equivalent algebraic form.
Definition 1 (31):
-
1
Let X be a row vector of dimension np and Y be a column vector of dimension p. Then we split X into p equal-size blocks as X1, X2, ..., XP, which are 1 × n rows. Define the STP, denoted by
 , as
, as 
-
2
Let A ∈ Mm×n and B ∈ Mp×q. If either n is a factor of p, say nt = p and denote it as
 , or p is a factor of n, say n = pt and denote it as
, or p is a factor of n, say n = pt and denote it as  , then we define the STP of A and B, denoted by
, then we define the STP of A and B, denoted by  , as the following: C consists of m × q blocks as C = (Cij) and each block is
, as the following: C consists of m × q blocks as C = (Cij) and each block is 
where Ai is the i-th row of A and Bj is the j-th column of B.
Example 1: Let  and
and . Then, one can obtain
. Then, one can obtain

Remark 1: It is noted that when n = p, STP of A and B turns into the conventional matrix produce. So, STP can be seen as a generalization of the conventional matrix product and all the fundamental properties of matrix product, such as distributive rule, associative rule, etc, still hold.
And, it can be verified that for two column vectors  and
and  ,
,  .
.
Some related properties of STP are collected as follows:
Proposition 1: Assume  , then (where
, then (where  refers to the Kronecker product, It is the identity matrix)
refers to the Kronecker product, It is the identity matrix)

Assume  , then
, then

Proposition 2: Assume A ∈ Mm×n is given,
-
1
Let
 be a row vector. Then,
be a row vector. Then, 
-
2
Let
 be a column vector. Then,
be a column vector. Then, 
For statement ease, some notations used in this article are defined as follows.
-
1
 denotes the r-th column of the n×n identity matrix In and
denotes the r-th column of the n×n identity matrix In and  , which is the set of all n columns of In.
, which is the set of all n columns of In. -
2
A matrix A ∈ Mn×m can be called a logical matrix if
 , which is briefly denoted by
, which is briefly denoted by  . And the set of n×m logical matrices is denoted by
. And the set of n×m logical matrices is denoted by 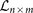 .
.
Next, we define the swap matrix  , let
, let  and
and  be two column vectors
be two column vectors

where W[m,n] is a mn × mn matrix labeled columns by  and rows by
and rows by  , the elements in position ((I, J), (i, j)) is
, the elements in position ((I, J), (i, j)) is

W[m,n] is briefly denoted by W[m].
Assume  and xi(t) ∈ Δ2, we can get
and xi(t) ∈ Δ2, we can get  , where
, where  . Here, Mr = δ4[1,4], which is power-reducing matrix and it can be verified that P2 = MrP,
. Here, Mr = δ4[1,4], which is power-reducing matrix and it can be verified that P2 = MrP,  .
.
In order to get the matrix expression of logical dynamics, the Boolean values should be denoted as vectors  and
and  . And the following lemma is fundamental for the matrix expression of logical functions.
. And the following lemma is fundamental for the matrix expression of logical functions.
Lemma 131: Any logical function  with logical arguments
with logical arguments  , can be expressed in a multi-linear form as
, can be expressed in a multi-linear form as

where Mf ∈ 2×2r is unique, which is called the structure matrix of logical function f.
More details on STP can be found in Ref. 31. In the following, the matrix products are assumed to be STP and the symbol  is omitted if no confusion arises.
is omitted if no confusion arises.
Main Results
Algebraic expression of asynchronous Boolean multiplex control networks with time delay
Regulatory entities in multiplex take part in several layers of networks, the states of which on different layers evolve independently. However, a final deterministic state of each entity should be obtained at the end of each time step determined by all of values on involved layers.
For a Boolean multiplex network with  nodes and
nodes and  layers, assume
layers, assume  accounts for the state of node i on layer l at time t. When time delay τ is considered in states, one can obtain
accounts for the state of node i on layer l at time t. When time delay τ is considered in states, one can obtain

where  is the update function of node i on layer l. Furthermore, assume
is the update function of node i on layer l. Furthermore, assume  represents the overall state of node i at time t. Refer to14, we can get
represents the overall state of node i at time t. Refer to14, we can get

where  is the canalizing function. Boolean functions are canalizing if whenever the canalizing variable takes a given value, the function always yields the same output, irrespective of the values of other variables14. Note that, strictly speaking, there exists an interval between the renewal of the value of node i on layer l, say
is the canalizing function. Boolean functions are canalizing if whenever the canalizing variable takes a given value, the function always yields the same output, irrespective of the values of other variables14. Note that, strictly speaking, there exists an interval between the renewal of the value of node i on layer l, say  and the overall state
and the overall state  in the whole multiplex. In the following discussion, based on an assumption that the interval between the above two states is instantaneous, the same time step t is used for both of them.
in the whole multiplex. In the following discussion, based on an assumption that the interval between the above two states is instantaneous, the same time step t is used for both of them.
Next, we introduce  controls with time delay τ into system (1), the corresponding dynamical control system can be described as
controls with time delay τ into system (1), the corresponding dynamical control system can be described as

where ui(t),  are controls and
are controls and  is the update rule of node i on layer l with controls.
is the update rule of node i on layer l with controls.
By means of Lemma 1, a structure matrix  can be calculated for each logical rule
can be calculated for each logical rule  , based on which one can obtain the algebraic form of Eq.(3) as follows.
, based on which one can obtain the algebraic form of Eq.(3) as follows.

where  ,
,  . Subsequently, the algebraic representation of Eq.(2) can be obtained as
. Subsequently, the algebraic representation of Eq.(2) can be obtained as

where  is the structure matrix of logical function
is the structure matrix of logical function  and
and  .
.
Under Harvey's asynchronous update, at each time step t, only one node is at random chosen for update. Hence, one can obtain

Multiplying all the  equations of system (6), one can get
equations of system (6), one can get

wher  is called as the control-depending network transition matrix, which involves all of the state transfer information of a dynamical control system.
is called as the control-depending network transition matrix, which involves all of the state transfer information of a dynamical control system.
In the following, respectively for two kinds of controls, the controllability of ABMCNs with time delay is to be discussed:
-
1
Controls come from a free Boolean sequence. Precisely, at time t,
 controls are freely designed and described as
controls are freely designed and described as  .
. -
2
The controls are determined by certain logical rules, which can be called input control networks:
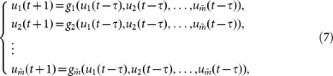
where
 are logical rules.
are logical rules.
Deterministic controllability of asynchronous Boolean multiplex control networks with time delay
Synchronous BNs are deterministic dynamical systems, however, under Harvey's asynchronous update scheme,  different update choices can be randomly chosen with the same probability at each time step. Correspondingly, when logical system is converted into linear form, there are
different update choices can be randomly chosen with the same probability at each time step. Correspondingly, when logical system is converted into linear form, there are  different control-depending network transition matrices
different control-depending network transition matrices  ,
,  . Say, the average probability for each transition matrix is
. Say, the average probability for each transition matrix is  . Then, one can obtain
. Then, one can obtain

Definition 2: Consider system (6) with time delay τ, given an initial state sequence  ,
,  , the destination state
, the destination state  is said to be controllable with probability one at time s > 0, if a group of controls u(t),
is said to be controllable with probability one at time s > 0, if a group of controls u(t),  can be found such that
can be found such that  . Noted that
. Noted that  is the smallest integer larger than or equal to a, for instance,
is the smallest integer larger than or equal to a, for instance,  .
.
Remark 2: When time delay τ and time s are given, according to the discussed model, i.e. Eq. (1), the previous location should be s−(1+τ), continue to induce, one can obtain  . Since an initial state sequence
. Since an initial state sequence  ,
,  is given, one can verify that location
is given, one can verify that location  should be in the scope of
should be in the scope of  , i.e. the initial state would be
, i.e. the initial state would be  ,
,  .
.
Definition 3: As to system (6) with time delay τ, when a control  exists such that state
exists such that state  holds
holds  ,
,  is said to be a control-depending fixed point.
is said to be a control-depending fixed point.
Theorem 1: Consider system (6) with time delay τ, when an initial state sequence  (
( ) is given, the destination state
) is given, the destination state  is said to be controllable at time s> 0 with probability one, only and if only state
is said to be controllable at time s> 0 with probability one, only and if only state  is a control-depending fixed point.
is a control-depending fixed point.
Proof:
(Sufficiency)Assume the destination state  is a control-depending fixed point of system (6) with time delay τ. According to Definition 3, a control
is a control-depending fixed point of system (6) with time delay τ. According to Definition 3, a control  can be found that
can be found that  . Consequently, we can find a group of controls u(t) = u,
. Consequently, we can find a group of controls u(t) = u,  . Then, one can obtain
. Then, one can obtain  from the initial state
from the initial state  . So,
. So,  can be controllable from itself with probability one at time s.
can be controllable from itself with probability one at time s.
(Necessity) When the destination state  is said to be controllable with probability one at time s>0 from initial state
is said to be controllable with probability one at time s>0 from initial state  ,
,  should be proved to be a control-depending fixed point. Firstly, we assume
should be proved to be a control-depending fixed point. Firstly, we assume  . According to Definition 2, a control u(s−τ−1) can be found that
. According to Definition 2, a control u(s−τ−1) can be found that  , which means
, which means  , where
, where  and
and  . When
. When  , considering the rule of Harvey's update scheme, there should be only one node
, considering the rule of Harvey's update scheme, there should be only one node  and the rest elements
and the rest elements  . And when
. And when  , there should be only one node
, there should be only one node  and the rest elements
and the rest elements  . The two results are contradictory. So the above assumption can't be held. Say,
. The two results are contradictory. So the above assumption can't be held. Say,  should be equal to
should be equal to  . Deduce the rest from this, one can obtain
. Deduce the rest from this, one can obtain  ,
,  . According to Definition 3, it can be proved that
. According to Definition 3, it can be proved that  should be a control-depending fixed point of system (6) with time delay τ.
should be a control-depending fixed point of system (6) with time delay τ.
This completes the proof.
From the above results, we can conclude that, as to system (6) with time delay τ, when two states  are given and
are given and  ,
,  can't be controllable from
can't be controllable from  with probability one. Hence, it is necessary and reasonable to discuss the controllability of the studied model from the perspective of probability.
with probability one. Hence, it is necessary and reasonable to discuss the controllability of the studied model from the perspective of probability.
Controllability of asynchronous Boolean multiplex control networks with time delay via free Boolean sequence
In this section, controls are assumed to be free Boolean sequences, based on which the controllability of studied model is discussed.
Definition 4: Given the initial state sequence  ,
,  and the destination state
and the destination state  , system (6) with time delay τ is said to be controllable to
, system (6) with time delay τ is said to be controllable to  with probability at time s > 0, if a group of controls u(t),
with probability at time s > 0, if a group of controls u(t),  can be found such that
can be found such that  .
.
When the initial states and a control sequence are specified, the following approach can be used to calculate the reachable set with probability at time s.
Before the next discussions, we define two operations:
-
1
 , furthermore, when
, furthermore, when  ,
,  . Correspondingly,
. Correspondingly,  and
and 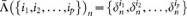 . For instance,
. For instance,  and
and  .
. -
2
Let column vector X ∈ Rm, all of row indies of X in which row elements aren't equal to zero compose a set denoted by Ω (X). For example, X = [1,0,2,1]T and Ω(X) = {1,3,4}.
Theorem 2: For system (6) with time delay τ, given the initial state sequence  ,
,  and controls u(t),
and controls u(t),  , the destination state
, the destination state  is reachable with probability at time s, iff
is reachable with probability at time s, iff

where  ,
,  ,
,  ,
,  and
and  represent the φ-th column of matrix.
represent the φ-th column of matrix.
Proof: By means of STP, system (6) with time delay τ can be rewritten as

At time t, since each node in multiplex has the same probability to be chosen for update, one can obtain the overall expected value of  as
as

Since time delay τ is involved both in states and controls, the location of the initial state which evolves into the destination state  is
is  . To expand the above formula and yields
. To expand the above formula and yields

where  .
.
This completes the proof.
When the initial states are given and controls are freely chosen, we provide the following approach to calculate the reachable set with probability at time s. Assume  is the set of initial states, we denote by R(X0)s,τ the reachable set from set X0 with time delay τ at time s under arbitrary controls.
is the set of initial states, we denote by R(X0)s,τ the reachable set from set X0 with time delay τ at time s under arbitrary controls.
Lemma 2: For system (6) with time delay τ,  is the set of initial states. Controls u(t),
is the set of initial states. Controls u(t),  can be freely chosen, one can obtain
can be freely chosen, one can obtain

where  ,
,  ,
,  and Row(·)i represents the i-th row of matrix.
and Row(·)i represents the i-th row of matrix.
Proof:
1) Assume state  ,
,  should be proofed.
should be proofed.
Since the destination state  is reachable with probability at time s, one can find a sequence of controls
is reachable with probability at time s, one can find a sequence of controls  to steer the system from initial state
to steer the system from initial state  to the destination states
to the destination states  . Correspondingly, based on Theorem 2, it's easy to get the element in the position (r, φ) of matrix
. Correspondingly, based on Theorem 2, it's easy to get the element in the position (r, φ) of matrix  should be non-zero, which means the φ-th element of row vector
should be non-zero, which means the φ-th element of row vector  is non-zero.
is non-zero.
2) When  , we can assume the φ-th element of row vector
, we can assume the φ-th element of row vector  is non-zero. According to Theorem 2, by means of
is non-zero. According to Theorem 2, by means of  , the destination states
, the destination states  is reachable with probability at time s. Furthermore,
is reachable with probability at time s. Furthermore,  can be decomposed into a sequence of controls as
can be decomposed into a sequence of controls as  .
.
This completes the proof.
And, when a control sequence is given, we also can obtain the specific reachable probability from certain initial states to a given destination state  at time s.
at time s.
Lemma 3: For system (6) with time delay τ, assume the initial state sequence as  ,
,  and controls as
and controls as  . The reachable probability from the initial states to the destination state
. The reachable probability from the initial states to the destination state  at time s is
at time s is

where  ,
,  ,
,  and (·)i,j is the element at position (i, j) of matrix.
and (·)i,j is the element at position (i, j) of matrix.
Remark3: Entry (β, φ) of matrix  indicate the state transfer information of dynamics from initial state
indicate the state transfer information of dynamics from initial state  under control sequence
under control sequence  after
after  time steps to destination state
time steps to destination state  .
.
Controllability of asynchronous Boolean multiplex control networks with time delay via input control networks
Based on STP of matrix, the linear representation of system (7) can be obtained as

where  is the network transient matrix of input control network.
is the network transient matrix of input control network.
Definition 5: Consider system (6) with input control network (7) and time delay τ, when initial state  and destination state
and destination state  are given,
are given,  is said to be controllable with probability from
is said to be controllable with probability from  at time s, if an initial control
at time s, if an initial control  can be found such that
can be found such that

where  .
.
Theorem 3: For system (6) with input control network (7) and time delay τ, the destination state  is controllable with probability from initial state
is controllable with probability from initial state  under initial control u0 at time s iff
under initial control u0 at time s iff

where  ,
,  ,
,  .
.
Proof:
One can obtain

This completes the proof.
Lemma 4: For system (6) with input control network (7) and time delay τ, when the initial control u0 can be freely chosen, the set of states which are reachable with probability from initial states  at time s is
at time s is

where  .
.
Lemma 5: For system (6) with input control network (7) and time delay τ, the probability from the initial states  to the destination state
to the destination state  under initial control u0 at time s is
under initial control u0 at time s is

where  .
.
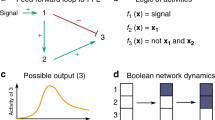
Examples
Example 1 Consider Boolean multiplex control network (16) with  layers,
layers,  nodes and
nodes and  control shown in Fig 2. Assume system (16) is under Harvey's asynchronous update and time delay τ both in states and controls.
control shown in Fig 2. Assume system (16) is under Harvey's asynchronous update and time delay τ both in states and controls.

where  ,
,  ,
,  ,
,  and
and  represent the logical functions of negation, disjunction, conjunction, implication and equivalence, respectively. Correspondingly, one can obtain the algebraic representation of logical functions as
represent the logical functions of negation, disjunction, conjunction, implication and equivalence, respectively. Correspondingly, one can obtain the algebraic representation of logical functions as  ,
,  ,
,  ,
, and
and  .
.
Based on the above discussion, we define  and
and  . And, as to the canalizing function
. And, as to the canalizing function  , without loss of the generality, we choose disjunction function, i.e.
, without loss of the generality, we choose disjunction function, i.e.  . The control u1(t) in system (16) is free Boolean variable. In the following, the controllability of ABMCNs (16) with time delay τ is to be discussed. Firstly, we calculate the control-depending network transition matrix of system. Note that, at time t,
. The control u1(t) in system (16) is free Boolean variable. In the following, the controllability of ABMCNs (16) with time delay τ is to be discussed. Firstly, we calculate the control-depending network transition matrix of system. Note that, at time t,  .
.
Case 1: at time t, when node 1 is selected for update,

Case 2: at time t, when node 2 is selected for update,

Case 3: at time t, when node 3 is selected for update,

Case 4: at time t, when node 4 is selected for update,

Therefore, all of the control-depending network transition matrices can be calculated as follows.


Assume time step s = 7 and time delay τ = 2, randomly choose the initial states  ,
,  and
and  . One can obtain
. One can obtain  and the initial state
and the initial state  . Respectively for the free control sequence is given or arbitrary, the reachable set of system (16) is discussed as follows.
. Respectively for the free control sequence is given or arbitrary, the reachable set of system (16) is discussed as follows.
One can obtain

Firstly, we assume the control sequence is specified. According to Theorem 2, controls  . Hence, when a control sequence is given as
. Hence, when a control sequence is given as  ,
,  ,
,  , one can obtain
, one can obtain  . By means of Theorem 2, the reachable set from initial state
. By means of Theorem 2, the reachable set from initial state  under the given controls at time 7 can be calculated as
under the given controls at time 7 can be calculated as

i.e., as to the nondeterministic system (16), there are totally 8 states which have the possibility to be reached under the specified controls from initial state  . Moreover, one can obtain the destination state
. Moreover, one can obtain the destination state  has the maximum probability 21/64.
has the maximum probability 21/64.
When the control sequence is arbitrary, based on Lemma 2, we can calculate the corresponding reachable set R(X0)s,τ. For matrix (17), the row vectors in 3th, 4th, 7th, 8th and 12th rows are zero, that mean states  are unreachable from the initial state
are unreachable from the initial state  with time step s = 7 and time delay τ = 2. Hence, we can obtain the reachable set
with time step s = 7 and time delay τ = 2. Hence, we can obtain the reachable set

In Fig 3, the reachable states of system (16) from  under free controls with time delay τ = 2 in 3 steps are depicted.
under free controls with time delay τ = 2 in 3 steps are depicted.
When a destination state is given, different controls can steer system from the initial states into the target with different probabilities. Since a control sequence can't be found to make system turn into the target with possibility one, hence, controls which can get the maximum probabilities become the focus of attention. In virtue of the matrix (17), we can conveniently obtain the expected control sequence. Assume  , the maximum probability 19/64 at (6, 1) of matrix (17), that means control
, the maximum probability 19/64 at (6, 1) of matrix (17), that means control  can steer the initial state
can steer the initial state  to destination state (1, 0, 1, 0) at time step 7 with probability 19/64. Subsequently, we can calculate
to destination state (1, 0, 1, 0) at time step 7 with probability 19/64. Subsequently, we can calculate  , i.e. u1(−2) = 1, u1(1) = 1, u1(4) = 1.
, i.e. u1(−2) = 1, u1(1) = 1, u1(4) = 1.
Example 2 In the process of the cell cycle, the onset of M (mitosis) and S (DNA replication) phases are directed by the periodic activation of cyclin-dependent kinases (cdk's). Romond et al.46 constructed the differential equations model to reflect the above dynamics and Heidel et al.4 proposed the corresponding Boolean model. Based on the previous studies, considering time delay in the process, Boolean control model was further extended into multiplex architecture as follows.

where +~Mp = δ2[2,1,1,2] and ·~Mc = δ2[1,2,2,2].
The controls in system (18) are produced by input control network as follows

By means of STP, one can obtain linear representation of system (19) as u(t + 1) = u1(t − τ)u2(t − τ) = Mnu2(t−τ)u1(t − τ) = MnW[2]u(t − τ) and G = MnW[2] = δ4[3,1,4,2].
Case 1: at time t, when node  is selected for update,
is selected for update,

Case 2: at time t, when node  is selected for update,
is selected for update,

Case 3: at time t, when node  is selected for update,
is selected for update,

Case 4: at time t, when node  is selected for update,
is selected for update,

Assume time step s = 9 and time delay τ = 3, randomly choose the initial states as  ,
,  ,
,  and
and  . One can obtain
. One can obtain  and the initial state
and the initial state  . According to Theorem 3, we can calculate that
. According to Theorem 3, we can calculate that


Using Lemma 4, when the initial control u0 is free, except three unreachable states  ,
,  and
and  , all of the rest states can be reachable from initial state
, all of the rest states can be reachable from initial state  at time s = 9 with time delay τ = 3. Furthermore, when initial control uρ is assumed to be specified, for instance,
at time s = 9 with time delay τ = 3. Furthermore, when initial control uρ is assumed to be specified, for instance,  , one can obtain the corresponding reachable set as follows.
, one can obtain the corresponding reachable set as follows.

Note that states  ,
,  and
and  can be reached with the same probability 0.1406 from initial state
can be reached with the same probability 0.1406 from initial state  under initial control uρ = (1,0) at time s = 9 with time delay τ = 3. Similarly, destination states
under initial control uρ = (1,0) at time s = 9 with time delay τ = 3. Similarly, destination states  and
and  can be reached with the same probability 0.1094, which is also the minimum reachable probability compared with the rest reachable states. Correspondingly, we can obtain the maximum reachable probability belonging to state
can be reached with the same probability 0.1094, which is also the minimum reachable probability compared with the rest reachable states. Correspondingly, we can obtain the maximum reachable probability belonging to state  is 0.3594.
is 0.3594.
In some applications, such as the therapeutic intervention, normally a final target is clear, i.e. an expected state for biological system is given. Hence, we should find a specific control sequence to steer system from the initial state to target with the maximum probability. Based on the above discussion, an approach can be obtained. Assume a required target at time s = 9 with time delay τ = 3 is  . By using of matrix (20), we can get the maximum reachable probability is 0.2656 at the Row 2 and Column 3. According to Theorem 3 and Lemma 5, we can calculate the initial control
. By using of matrix (20), we can get the maximum reachable probability is 0.2656 at the Row 2 and Column 3. According to Theorem 3 and Lemma 5, we can calculate the initial control  , i.e. u1(0) = 0 and u2(0) = 1.
, i.e. u1(0) = 0 and u2(0) = 1.
Conclusions
In this article, inputs as controls are introduced into Boolean multiplex networks under asynchronous stochastic update, meanwhile, time delay as additional factor is considered both in states and inputs of system. By means of STP approach, the above logical dynamics is converted into algebraic form and the controllability of dynamics is discussed. Firstly, it is proved that only control-depending fixed points can be controlled with probability one, which means the discussion of controllability of asynchronous Boolean control networks should be in terms of probabilities. Subsequently, respectively for two kinds of controls, formulae to calculate the reachable set from an initial state to a destination state under specified controls or arbitrary controls are provided, as well as the approach to obtain the specific reachable probabilities from an initial state to different destination states. Moreover, we also present how to find a precise control sequence which can steer dynamics into a given target with the maximum reachable probability.
References
Kauffman, S. A. Metabolic stability and epigenesis in randomly constructed genetic nets. J. theor. Biol. 22, 437–467 (1969).
Dubrova, E. & Teslenko, M. Compositional properties of random Boolean networks. Phys. Rev. E 71, 056116 (2005).
Ghanbarnejad, F. & Klemm, K. Stability of Boolean and continuous dynamics. Phys. Rev. Lett. 107, 188701 (2011).
Heidel, J., Maloney, J., Farrow, C. & Rogers, J. A. Finding cycles in synchronous Boolean networks with applications to biochemical systems. Int. J. Bifurcat. Chaos 13, 535–552 (2003).
Dubrova, E. & Teslenko, M. A SAT-Based Algorithm for Finding Attractors in Synchronous Boolean Networks. IEEE ACM T. Comput. Bi. 8, 1393–1399 (2011).
Zheng, D. et al. (2013) An efficient algorithm for computing attractors of synchronous and asynchronous Boolean networks.Plos One 8, e60593 (2013).
Ching, W. K. et al. Optimal control policy for probabilistic Boolean networks with hard constraints. IET Syst. Biol. 23, 90–99 (2008).
Rosin, D. P., Rontani, D., Gauthier, D. J. & Schöll, E. Control of Synchronization Patterns in Neural-like Boolean Networks. Phys. Rev. Lett. 110, 104102 (2013).
Politano, G. et al. Using Boolean networks to model post-transcriptional regulation in gene regulatory networks. J. Comput. Sci. 5, 332–344 (2014).
Hashemikhabir, S. et al. Large-Scale Signaling Network Reconstruction. IEEE ACM T. Comput. Bi. 9, 1696–1708 (2012).
Davidich, M. I. & Bornholdt, S. Boolean Network Model Predicts Knockout Mutant Phenotypes of Fission Yeast. Plos One 8, e71786 (2013).
Yan, K. K. et al. Comparing genomes to computer operating systems in terms of the topology and evolution of their regulatory control networks. Proc. Nat. Acad. Sci. U.S.A. 107, 9186–9191 (2010).
Kitano, H. Systems biology: a brief overview. Science 295, 1662–1664 (2002).
Cozzo, E., Arenas, A. & Moreno, Y. Stability of Boolean multilevel networks. Phys. Rev. E 86, 036115 (2012).
Mucha, P. J. et al. Community structure in time-dependent, multiscale and multiplex networks. Science 328, 876–878 (2010).
Bianconi, G. Statistical mechanics of multiplex networks: Entropy and overlap. Phys. Rev. E 87, 062806 (2013).
Granell, C., Gomez, S. & Arenas, A. Dynamical interplay between awareness and epidemic spreading in multiplex networks. Phys. Rev. Lett. 111, 128701 (2013).
Gómez, S. et al. Diffusion dynamics on multiplex networks. Phys. Rev. Lett. 110, 028701 (2013).
Gómez-Gardeñes, J., Reinares, I., Arenas, A. & Floría, L. M. Evolution of cooperation in multiplex networks. Sci. Rep. 2, 620 (2012).
Gómez-Gardeñes, J., Gracia-Lázaro, C., Floría, L. M. & Moreno, Y. Evolutionary dynamics on interdependent populations. Phys. Rev. E 86, 056113 (2012).
Hallinan, J. & Wiles, J. Asynchronous dynamics of an artificial genetic regulatory network. In: Artificial Life IX: Proceedings of the Ninth International Conference on the Simulation and Synthesis of Living Systems (eds. Pollack, J., et al.) 399–403 (MIT Press Cambridge MA, 2004).
Harvey, I. & Bossomaier, T. Time out of joint: Attractors in asynchronous random Boolean networks. In: Proceedings of the Fourth European Conference on Artificial Life (eds. Husbands, P. & Harvey, I.) 67–75 (MIT Press Cambridge MA, 1997).
Greil, F. & Drossel, B. The dynamics of critical Kauffman networks under asynchronous stochastic update. Phys. Rev. Lett. 95, 048701 (2005).
Greil, F., Drossel, B. & Sattler, J. Critical Kauffman networks under deterministic asynchronous update. New J. Phys. 9, 373 (2007).
Saadatpour, A., Albert, I. & Albert, R. Attractor analysis of asynchronous Boolean models of signal transduction networks. J. Theor. Boil. 266, 641–656 (2010).
Tournier, L. & Chaves, M. Interconnection of asynchronous Boolean networks, asymptotic and transient dynamics. Automatica 49, 884–893 (2013).
Zhu, P. & Han, J. Asynchronous stochastic Boolean networks as gene network models. J. Comput. Biol. 10.1089/cmb.2014.0057 (2014).
Jack, J., Wambaugh, J. F. & Shah, I. Simulating quantitative cellular responses using asynchronous threshold Boolean network ensembles. BMC Syst. Boil. 5, 109 (2011).
Shmulevich, I., Dougherty, E. R., Kim, S. & Zhang, W. Probabilistic Boolean networks: a rule-based uncertainty model for gene regulatory networks. Bioinformatics 18, 261–274 (2002).
Kim, J., Park, S. M. & Cho, K. H. Discovery of a kernel for controlling biomolecular regulatory networks. Sci. Rep. 3, 2223 (2013).
Cheng, D., Qi, H. & Li, Z. Analysis and Control of Boolean Networks: A Semi-Tensor Product Approach (Springer-Verlag, London, U.K. 2011).
Klamka, J. Controllability of dynamical systems. A survey. B. Pol. Acad. Sci-Tech. 61, 335–342 (2013).
Jia, T. & Barabási, A. L. Control capacity and a random sampling method in exploring controllability of complex networks. Sci. Rep. 3,2354 (2013).
Cheng, D. & Qi, H. Controllability and observability of Boolean control networks. Automatica 45, 1659–1667 (2009).
Li, F. F. & Sun, J. T. Controllability of Boolean control networks with time delays in states. Automatica 47, 603–607 (2011).
Li, F. F. & Sun, J. T. Controllability and optimal control of a temporal Boolean network. Neural Networks 34, 10–17 (2012).
Han, M., Liu, Y. & Tu, Y. Controllability of Boolean control networks with time delays both in states and inputs. Neurocomputing 129, 467–475 (2014).
Li, F. F. & Sun, J. T. Controllability of higher order Boolean control networks. Appl. Math. Comput. 219, 158–169 (2012).
Chen, H. & Sun, J. A new approach for global controllability of higher order Boolean control network. Neural Networks 39, 12–17 (2013).
Laschov, D. & Margaliot, M. Controllability of Boolean control networks via the Perron-Frobenius theory. Automatica 48, 1218–1223 (2012).
Luo, C., Wang, X. Y. &. Liu, H. Controllability of asynchronous Boolean multiplex control networks. Chaos 24, 033108 (2014).
Wang, Z., Gao, H., Cao, J. & Liu, X. On delayed genetic regulatory networks with polytopic uncertainties: robust stability analysis. IEEE T. NanoBiosci. 7, 154–163 (2008).
Granell, C., Gomez, S. & Arenas, A. Dynamical Interplay between Awareness and Epidemic Spreading in Multiplex Networks. Phys. Rev. Lett. 111, 128701 (2013).
Yang, P., Xie, G. & Wang, L. Controllability of linear discrete-time systems with time-delay in state and control. Int. J. Control 82, 1288–1296 (2009).
Li, F. F. & Sun, J. T. Controllability of probabilistic Boolean control networks. Automatica 47, 2765–2771 (2011).
Romond, P. C., Rustici, M., Gonze, D. & Goldbeter, A. Alternating oscillations and chaos in a model of two coupled biochemical oscillators driving successive phases of the cell cycle. Ann. N.Y. Acad. Sci. 879, 180–193 (1999).
Acknowledgements
This research is supported by the National Natural Science Foundation of China (Nos: 61402267, 61370145, 61173183, 61472232, 60973152, 60970004 and 61272094), the Superior University Doctor Subject Special Scientific Research Foundation of China (No: 20070141014), Program for Liaoning Excellent Talents in University (No: LR2012003), the National Natural Science Foundation of Liaoning province (No: 20082165) and the Fundamental Research Funds for the Central Universities (No: DUT12JB06).
Author information
Authors and Affiliations
Contributions
L.C., W.X.Y. devised the model and carried out theoretical analysis. L.C. and L.H. implemented numerical simulations. L.C., W.X.Y. and L.H. wrote the main text of the manuscript.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Rights and permissions
This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivs 4.0 International License. The images or other third party material in this article are included in the article's Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder in order to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-nd/4.0/
About this article
Cite this article
Luo, C., Wang, X. & Liu, H. Controllability of time-delayed Boolean multiplex control networks under asynchronous stochastic update. Sci Rep 4, 7522 (2014). https://doi.org/10.1038/srep07522
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep07522
This article is cited by
-
A survey on applications of semi-tensor product method in engineering
Science China Information Sciences (2018)
-
Observability of Boolean multiplex control networks
Scientific Reports (2017)
-
A simplified computational memory model from information processing
Scientific Reports (2016)
-
Synchronization Analysis of Master-Slave Probabilistic Boolean Networks
Scientific Reports (2015)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.



 , as
, as 
 , or p is a factor of n, say n = pt and denote it as
, or p is a factor of n, say n = pt and denote it as  , then we define the STP of A and B, denoted by
, then we define the STP of A and B, denoted by  , as the following: C consists of m × q blocks as C = (Cij) and each block is
, as the following: C consists of m × q blocks as C = (Cij) and each block is 
 be a row vector. Then,
be a row vector. Then, 
 be a column vector. Then,
be a column vector. Then, 
 denotes the r-th column of the n×n identity matrix In and
denotes the r-th column of the n×n identity matrix In and  , which is the set of all n columns of In.
, which is the set of all n columns of In. , which is briefly denoted by
, which is briefly denoted by  . And the set of n×m logical matrices is denoted by
. And the set of n×m logical matrices is denoted by 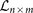 .
. controls are freely designed and described as
controls are freely designed and described as  .
.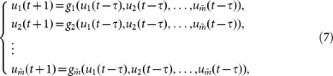
 are logical rules.
are logical rules. , furthermore, when
, furthermore, when  ,
,  . Correspondingly,
. Correspondingly,  and
and 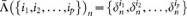 . For instance,
. For instance,  and
and  .
.
