Abstract
We propose a new design of complex self-evolving structures that vary over time due to environmental interaction. In conventional 3D printing systems, materials are meant to be stable rather than active and fabricated models are designed and printed as static objects. Here, we introduce a novel approach for simulating and fabricating self-evolving structures that transform into a predetermined shape, changing property and function after fabrication. The new locally coordinated bending primitives combine into a single system, allowing for a global deformation which can stretch, fold and bend given environmental stimulus.
Similar content being viewed by others
Introduction
Additive manufacturing has captured the world's imagination since its first invention in 1984 by Charles Hull1, (known as the inventor of stereolithography and founder of 3D systems) who envisioned the technique as a new process for material prototyping before mass production. Printing technologies have developed at an exceptional pace in accuracy, speed, material property and manufacturing cost. As a research field, 3D printing tends to be interdisciplinary: innovations include conductive materials for printed circuits2, multi-material printing3,4 and scalability of printing technology5. Adding computational capability allows for printing structures with more complex geometry6 and even controlling the deformation behavior7. In this paper we wish to harness the huge potential of 3D printing to generate self-transforming structures with complex geometry. The necessity of such capabilities is unquestionable as we face a revolution in the robotic industry moving towards small and soft tools replacing traditional robotic mechanisms. Soft robotics have become extremely popular in the recent years, trying to mimic biology by creating soft and stiff controllable devices especially for the medical community. The main research directions, as summarized in19, are based on electromagnetic motor-driven engines25, temperature changing materials (Shape Memory Alloy)21,22, electric fields (Electroactive Polymer)23, pressurized fluids or gases24, chemical stimuli19 and light20. Each approach has different strain/stress bounds and response velocity. We must note that due to its importance and recent developments it is a highly investigated topic and we have merely covered the most common approaches.
In this paper, we consider fabrication of self-evolving structures where multiple materials can react to the environment and deform over time. To realize self-evolving functionality, it is necessary to fuse the insight from design into an engineered framework. On the hardware side, the system requirements include complex material programmability, multi-material printing and a variety of highly specific joint designs for folding, curling, twisting, linear expansion/shrinkage and a number of other transformations. Adding the extra dimension of time requires computation to play a more pivotal role in the fabrication process. Specifically, the requirements include a sophisticated simulation of topology transformations that contain the fabrication and material constraints, coupled with material optimization for efficient structures.
We propose a “design-fabrication-simulation” workflow for self-evolving structures. Our main contributions lie in three aspects:
Design: We propose a computational approach for designing self-evolving structures that vary over time due to environmental interaction.
Fabrication: We provide an implementable framework by specifying readily printable self-evolving elements that pair with computational models.
Simulation: We realistically imitate the deformation of the materials for enhancing design capabilities.
Related work:
Self-evolving structures were first introduced by utilizing hydrophilic materials that expand when submerged in water to induce geometric folding, curling, expansion and various other programmed shape changes. Researchers have demonstrated a variety of techniques using different approaches. However, the previous designs have focused on the transformation of simple shapes where manual modeling and empirical testing was used in construction8,9. A different approach based on folding of planar sheets10,11 has shown to be successful in optimizing designs in the context of material properties, where different activation methods, such as heat and microwaves, were explored12,13. In this work we show how to construct and simulate complex solid structures that bend and stretch over time. For the first time, we also demonstrate a non-trivial self-evolved structure where both stretching and bending of a 2D grid skeleton are considered.
Methods
Alignment of curves and surfaces
A first step was to align the initial and final status of the models. From this alignment we derived the angles and lengths required to fabricate self-evolving structures. Curves have a trivial (natural) parameterization, hence mapping between curves can be reduced to length normalization. For surfaces a more sophisticated alignment is required. Mapping between deformable shapes has been well characterized in literature. Gauss's Theorema Egregium (Latin for “remarkable Theorem”) states that the Gaussian curvature is an intrinsic invariant property, which is not influenced by the ambient space. It immediately follows that isometric shapes have similar Gaussian curvature. There are existing methods of alignment based on length preserving by minimizing the Gromov Hausdorff distance14, considering mapping in different ambient spaces15 and using conformal (angle preserving) mappings16. The latter is popular in texture mapping, given that a solution always exists that allows mapping of images onto complex surfaces. The drawback is the inevitable stretching, which is quantified by the conformal factor of the mapping.
In this work, we wish to deform a grid G from its planar structure into a surface with effective curvature. As no precise solution exists, we experimented with three different approaches: 1) A length preservation approach14, 2) a conformal mapping approach17 and 3) a simpler approach where bars remain within a single plane, which we refer to as sectional mapping in this paper. For isometric shapes, such as a plane and a cylinder, both length preserving and conformal mappings have perfect and similar solutions. When stretching occurs, we empirically found the sectional mapping produced relatively convincing results in our fabricated models despite its simplicity.
Workflow
The curve and grid deformation designed in the previous section can be equivalently described as length varying and position changing of joints and bars. Accordingly, in this design stage, we propose three primitives with two different models for stretching and another model for folding. As we will show later, these basic primitives are sufficient to print a diversity of models. To fabricate a self-evolving structure we embed dynamic segments into a printed structure, by printing with two materials that react differently when exposed to water. In particular, we use a hydrophilic polymer that absorbs water to increase in size. During design, the degree and amount to which these primitives stretch and fold should be adjusted and determined in relation to the desired shape. Importantly, the length, angular value and class of the primitives are all controllable parameters whose proper selection allows, for example, an initial 3D printed shape to deform into a desired shape, on its own.
Design
We present three different primitives, as shown in Figure 1:
- a
Linear stretching primitive: This primitive is able to change its length over time in the presence of water. It can be fabricated by integrating an expanding material into repeated circular disks. We used a cross/circle with a thickness of 0.813 mm and an expanded thickness of 1.245 mm. By adjusting the ratio of the expanding material to the rigid portions we can precisely control the percentage of linear expansion of the joint.
- b
Ring stretching primitive: An alternative fabrication of stretching primitives is implemented as a ring-like shape. We printed each ring with two layers; the inner ring and the outer ring are made of the two different materials. Once activated by water, the inner ring expands and forces the ring to deform into a bar shape longer than its original formation. By adjusting the radius of the ring we can precisely control the linear expansion after submerged in water.
- c
Folding primitive: Similar to the stretching primitives, we utilized the hydrophilic expanding material to enable folding. A strip of expanding material is printed over a corresponding strip of rigid material, which causes the primitive to fold. Switching the material order, i.e., printing the rigid material on top of the expanding material causes the joint to fold in the other direction. To specify the final angle, rigid disks are placed in between the bars that physically hit one another to stop the folding. The spacing and diameters of these disks can be adjusted to specify a desired folding angle. We control the folding direction in space (
 ) of this primitive by rotating the expanding and rigid strips with relation to the bars. This approach provides an additional degree of freedom in folding angles, as the plane in which the bars fold can also be controlled, as shown in Figure 2B.
) of this primitive by rotating the expanding and rigid strips with relation to the bars. This approach provides an additional degree of freedom in folding angles, as the plane in which the bars fold can also be controlled, as shown in Figure 2B.Figure 2 (A) Stratasys Connex 500 Multi-Material 3D Printer. (B) Folding primitive in
 requires two degrees of freedom. One angle is achieved by changing the spaces between the inner disks, which provides a physical stop once the end angle is reached. The second angle is maintained by changing the angles in between two neighboring bars. One can consider it as a rotational shift that changes the plane in which the bars fold. (C) A complete example embedding dynamic primitives of stretching and folding on a grid. This grid can accommodate a self-evolving deformation into a complex structure with both convex and concave parts. (D) Calibration of the folding joints is performed by repeated experiments on a planar hexagon. See Table 1 and Table 2 for angular and temporal measurements. (E) True fabrication measurements of bending elements.
requires two degrees of freedom. One angle is achieved by changing the spaces between the inner disks, which provides a physical stop once the end angle is reached. The second angle is maintained by changing the angles in between two neighboring bars. One can consider it as a rotational shift that changes the plane in which the bars fold. (C) A complete example embedding dynamic primitives of stretching and folding on a grid. This grid can accommodate a self-evolving deformation into a complex structure with both convex and concave parts. (D) Calibration of the folding joints is performed by repeated experiments on a planar hexagon. See Table 1 and Table 2 for angular and temporal measurements. (E) True fabrication measurements of bending elements.
(A) Left: rendered illustration of the linear stretching primitive. It is an assembly of rigid disks with expanding materials in the middle. By adjusting the ratio of expanding materials to rigid disks, it is possible to control the length of stretching. Right: video frames of the fabricated primitive stretching in water over time. (B) Left: rendered illustration of the ring stretching primitive. This is based on expansion of the ring shape into a bar. We adjust the stretching length by controlling the radius of the ring. Right: video frames of the fabricated primitive stretching in water over time. (C) Left: rendered illustration of the folding primitive. This design is also composed of bars and disks. The disks in the center act as stoppers. By adjusting the distances between the stoppers it is possible to set the final folding angle. Right: video frames of the fabricated primitive folding in water over time.
Calibration between the materials and desired angles/lengths were performed empirically on physically printed models. The two stretching primitives are relatively simple to calibrate. As stated above, the linear stretching primitive expands by 0.432 mm (from 0.813 mm to 1.245 mm) per disk when submerged in water, hence, the number of required disks is trivially evaluated. The ring stretching primitive simply follows basic geometry rules, where half of its circumference becomes the deformed length. In Figure 2D we present a calibration process for the folding primitive, by using a hexagon on the plane as an example. By repeating the experiments multiple times, we create a lookup table containing the angular and temporal information for this example, as shown in Table 1 and Table 2. The calibrated data serves as a guide for fabricating other structures composed of the same primitives.
Fabrication
The physics of 4D printing often requires multiple materials to be embedded into a single 3D structure. For example, the materials needed for fabrication of primitives (especially the joint component) may be different from the material used in the main structure. We use the Stratasys Connex 500 multi-material 3D printer with a spatial resolution of 300DPI, which is approximately 85 micrometer in the XY axes and about 30 micrometer in the Z axis (depth) (Figure 2A). The printing time of our method varies from one hour to eight hours depending on shape and complexity.
The Connex printer deposits a UV curable polymer using inkjet heads and cures layer by layer using UV light to create the complete 3D structure. This printer is able to print materials with different properties (such as color, hardness and transparency) simultaneously. It enables us to arrange the stretching and folding primitives in different orientations, which allows stretching and folding to happen at the desired position in the 3D vector space. Moreover, it can be used to generate Digital Materials (DMs) that represent distinct combinations of both components in different proportions and spatial arrangements. A DM inherits its properties from the parent materials and its structure can be digitally adjusted to have any set of properties in the available range. Since the mixing occurs on the tray, the spatial arrangement of the components plays a significant role in the generated DM characteristics and it provides additional flexibility in the DM engineering process. The generated parts are printed with a rigid plastic base and a material that expands upon exposure to water. The expanding material is a very hydrophilic UV curable polymer with low cross-link density that when exposed to water it absorbs and creates a hydrogel with up to 200% of the original volume. It is composed of hydrophilic acrylated monomers that create linear chains upon polymerization with a small amount of difunctional acrylate molecules. Such crosslink alter the properties of the polymer from water soluble to water swellable. The materials in usage are patent protected by US patent application number US14/189,819 and PCT patent application PCT/US14/018373. The components properties appear in Table 3. The rigid (black) materials have a 2 GPa elastic modulus and the poison ratio of 0.4. The expanding material (red) has an elastic modulus of 40 MPa in the dry state and 5 MPa in the fully swelled state. Its poison ratio is approximately 0.5.
Simulations
We have formulated our simulation using a spring-mass model with nonlinear constraints, to fully encompass the stretching and folding behaviors observed in our design and fabrication and to avoid shearing or twisting forces. For robustness, we utilize an industry standard approach to model solid deformations. Our simulator is based on the Nucleus system18 from Autodesk embedded in a design platform called Project Cyborg, with additional functionality to better simulate the temporal behavior of our materials. In what follows, we elaborate on the constraints of length, shear and twist and provide the geometric construction of the models. In Appendix A we provide a short description of the forces and damping in a spring-mass model and in Appendix B we elaborate on the simulator. We should emphasize that we do not simulate the movement in the molecular level but learned the kinematics movement of the entire model.
Simulation primitives
Rigid motion of bars: Parts of the model should be kept as close to rigid as possible during the simulation, namely bars, as illustrated Figure 3A. We force the bars to be rigid by adding constraints on the length in between the bar's sampled points. As shear and twist forces occur in practice, we force additional non-linear constraints on angles measured between edges and angles measured between the normal vector to the bar's surfaces.
(A) Renderings of an initial joint and its folding (upper row), with their corresponding spring-mass systems shown in the lower row. The lateral black springs represent the rigid bars and disks. The red springs represented the links that cause the joint to fold. (B) Variables in this schematic are used for calculation of stiffness coefficients. (C) Illustration of computing the joint length. Each joint is modeled using two disks and the length of each inner limb is calculated according to its distance from the center of rotation. The center link (marked as purple) remains constant in time. (D) Illustrations of the folding angle and axis. (E) Illustration of computing the bar length for a folding and stretching element. We evaluate the angles between connected bars α, β and the bending radius r. The length of the centered section (marked as purple) remains constant in time, while the length of the remaining elements (e.g. a) are approximated accordingly.
Stretching primitives (linear and ring): Two different stretching primitives are fabricated, both are similar and can be implemented as a spring-mass. We put two disks between the bars as shown in Figure 3. The forces between the disks, reflecting the folding of joints, are modeled using springs called links. Links push or pull the connected particles spreading the force inward and outward to stretch a joint. The spring's stiffness coefficient remains constant and the rest length is evaluated from the desired length measurement according to the predetermined shape. We uniformly sampled the length change of the primitive and as the simulation progresses we update the desired rest length. This approach provided a smooth deformation while compensating for a jiggling effect of a spring system even for small stiffness coefficients.
Folding primitives: A folding of a joint is simulated in a similar manner as the stretching primitives. The structure of disks and links are exactly the same, however, the asymmetric geometry is unique. A folding joint has different resting lengths in each location, while a stretching bar has the same rest length in all directions. The number of links is a discrete factor, since the bars are round cylinders. The stiffness coefficient selected for all of the links is constant and the direction of the folding is controlled by the rest length of each spring. Note that the folding in both  and
and  can be simulated in the same manner, i.e., controlling the folding by the final rest length. As before, the length constraint is uniformly sampled and updated as the simulation progressed.
can be simulated in the same manner, i.e., controlling the folding by the final rest length. As before, the length constraint is uniformly sampled and updated as the simulation progressed.
Evaluating angles and distances
From initial and final alignment we evaluated the desired rest lengths of all springs in the system for each time step. In what follows, we elaborate on folding elements and folding with additional stretching.
Folding: Each joint is modeled using two disks, as illustrated in Figure 2C and the length between two disks is calculated according to its distance from the center of rotation. We further assume that the center link (marked as purple in the Figure 2C) remains constant. We denote by D the disk's diameter and by d the disk's thickness. Given N disks the radius of the folding angle α can be approximated as  . Further denoting r as the folding radius, we can evaluate the total length l, which is the length of the center joint (purple curve), as
. Further denoting r as the folding radius, we can evaluate the total length l, which is the length of the center joint (purple curve), as

We divided the joint by uniformly inserting the disks, hence, for these N + 1 links each of the segment will have a length of l/(N + 1). Finally, the length of all other links (marked as red lines in Figure 2C), are evaluated using triangular similarity.
Folding with additional stretching: Once stretching is added to the system we provide additional elasticity to the tips of the bars while preserving the length of the centered section (marked as purple in the Figure 2E). As before we evaluate the angle between connected bars, however, we now consider two angles on both sides of the bar, denoted as α and β. We further denote the length of a bar i in between joints Pi and Pi+1 as Li and the length of the joints which is the sum of their center links as  and
and  , respectively. The latter were calculated as was described above. Now, the center section of a bar is approximated as
, respectively. The latter were calculated as was described above. Now, the center section of a bar is approximated as

From the dual radius folding angles α, β and centered bar length Li we approximate the remaining rest length of the bar's springs. As can be seen in Figure 2E, we first consider one folding radius as the mean of a double sided folding by

and it immediately follows that for an arbitrary spring a of radius d its rest length becomes  .
.
Results
In this section, we show that a broad diversity of shapes with complex geometries can be fabricated and simulated in a self-evolving manner.
1D folding
Our first fabricated model presents a time evolving curve in the plane. We initiate the system with an arbitrary set of connected letters “MIT” and converge to into another pre-defined formation similar to “SAL”. We aligned the curves and followed the joint-bar duality. We provide the time line (key frames) of this process in Figure 4C.
(A) Deformation of a grid into a sinusoidal wave. From left to right and top to bottom, we observe the grid as it folds into the desired shape. Only angular primitives were used. (B) Deformation of a grid into a hyperbolic surface. On the top we visualize the fabricated model and on the bottom the simulated version. The final deformation provides a reasonable approximation despite using only folding bars in the simulation. (C) Fabricating a time-varying curve. From left to right and top to bottom, the curve deforms over time to a different shape.
2D folding
We fabricated a sinusoidal wave (Figure 2A) and a hyperbolic surface (Figure 2B) to show the deformation of a 2D grid. In these examples, only rigid folding joints are used, while stretching primitives are not embedded. The sinusoidal wave is isometric to the grid and the Gaussian curvature remains zero, thus, folding alone provides strong results. For a hyperbolic surface, since stretching occurs, we only obtain the approximated final deformation, yet the result is reasonably accurate.
2D folding and stretching
The final fabricated model demonstrates both stretching and folding behaviors in a single structure. We fabricated a double curvature (convex and concave) surface with ring stretching primitives. The self- evolving deformation is shown in Figure 5.
Deformation of a grid into a double curvature surface (convex and concave).
The time line follows the orders of left to right and top to bottom. The printed schematics (initial grid) can be seen in Figure 2C.
A common phenomenon seen in all of the experiments relates to the self-transformation due to the properties of the material and design geometric mechanisms. We tested the repeatability of the transformation due to wetting and the reversibility due to drying. We repeatedly cycled wetting/folding and drying/unfolding for 20 consecutive cycles. We witnessed mechanical degradation on the 5th and 19th cycles. Similarly, we recorded the precise expansion of the material, drying of the material as well as prolonged wetting to watch for visual degradation. We have not witnessed any degradation of the expanding material while submerged underwater for 2 full weeks. However, we have witnessed degradation of the expanding material once a component is removed from the water and the material is dry. These results suggest that there is mechanical degradation due to repeated folding/unfolding and degradation of the expanding material due to wetting/drying cycles.
Discussion and limitation
In this new mechanical design we introduce hydrophilic materials for actively controlled temporal deformations. Since surfaces stretch during the process we constructed a locally coordinated bending geometry for achieving a global stretching property. Several limitations must be taken into consideration:
- 1
The linear expansion is fragile and limited to 30% of the linear stretching primitive, which can be improved by exploring new materials. Although the ring stretching primitive does not suffer from this limitation, the spatial sampling of the grid restricts it.
- 2
Reversibility of the transformation may be currently limited if the desired application requires many cycles of folding/unfolding or wetting/drying. Further testing is required to fully understand the complete lifespan of the materials and the degradation. However, our initial tests suggest that there is mechanical degradation due to many cycles of repeated folding/unfolding and degradation of the expanding material due to repeated wetting/drying cycles. However, with a small number of cycles the parts are able to fully recover their original shape upon drying and once dipped in water again, they transform once more.
- 3
We have only explored behavior of the structure due to water immersion, while other activating mechanisms such as heat and light can be used and are currently in development.
- 4
The simulation based on a spring-mass system provides strong results, however, the physical system is not constructed of springs and masses, which means that a solid simulation might provide more realistic results. In the future, we plan to evaluate the physical properties of the expanding materials and simulate their behavior on the molecular level.
Conclusions
This paper addresses the challenge of self-evolving complex structures. Traditional mechanical means of stretching, folding and bending are now replaced by expanding printed materials. We showed that a solid surface can be programmed to sense the environment and actively self-deform. The new primitives are rich enough to construct multi-purpose structures that can change their geometry. We are facing an era where design of soft deformable structures will alter industry and consequently our lives. Adaptive manufacturing became accessible to all, and, in our humble opinion, self deforming structures will be one of its most important descendant. In this paper we provide a first glance in designing, simulating and manufacturing printed time evolving structures required in many future applications.
References
Hull, C. W. inventor; Apparatus for production of three-dimensional objects by stereolithography. United States patent US 4,575,330. 1984.
Kawahara, Y., Hodges, S., Cook, B. S., Zhang, C. & Abowd, G. D. Instant Inkjet Circuits: Lab-based Inkjet Printing to Support Rapid Prototyping of UbiComp Devices. Paper presented at ACM International Joint Conference on Pervasive and Ubiquitous Computing, Seattle (2013).
Zhou, C., Chen, Y., Yang, Z. & Khoshnevis, B. Digital material fabrication using mask-image-projection-based stereolithography. Rapid Prototyping J. 19, 153–165 (2012).
Ahn, N. Y. et al. Omnidirectional printing of flexible, stretchable and spanning silver microelectrodes. Science. 323, 1590–1593 (2009).
Zhou, C. & Chen, Y. Additive manufacturing based on optimized mask video projection for improved accuracy and resolution. J of Manufacturing Processes, 14, 107–118 (2012).
Bacher, M., Bickel, B., James, D. L. & Pfister, H. Fabricating articulated characters from skinned meshes. ACM Trans. Graph. 31 (2012).
Bickel, B. et. al. Design and fabrication of materials with desired deformation behavior. ACM Trans. Graph. 29 (2010).
Cheung, K. C., Demaine, E. D., Bacharach, J. R. & Griffith, S. Programmable assembly with universally foldable strings. IEEE Trans. on Robotics, 27 (2011).
Tibbits, S. 4D Printing: Multi-Material Shape Change. Arch. Design. 84, 116–121 (2014).
Hawkes, E. et al. Programmable matter by folding. Proc. Nat. Acad. Sci. U.S.A. 107, 12441–12445 (2010).
Demaine, E. D. & Demaine, M. L. Recent Results in Computational Origami. Paper presented in the 3rd International Meeting of Origami Science, Math and Education, Asilomar (2001).
Yasu, K. & Inami, M. POPAPY: Instant Paper Craft Made Up in a Microwave Oven. Paper presented at the 9th International Conference on Advances in Computer Entertainment, Kathmandu (2012).
Ge, Q., Qi, H. J. & Dunn, M. L. Active materials by four-dimension printing. Appl. Phys. Lett. 103 (2013).
Bronstein, A. M., Bronstein, M. M. & Kimmel, R. Generalized multidimensional scaling: a framework for isometry-invariant partial surface matching. Proc. Nat. Acad. Sci. U.S.A. 103, 1168–1172 (2006).
Bronstein, A. M., Bronstein, M. M. & Kimmel, R. Three-dimensional face recognition. Int. J. Com. Vis. 64, 5–30 (2005).
Lipman, Y. & Funkhouser, T. Mobius voting for surface correspondence. ACM Trans. Graph. 28 (2009).
Aflalo, Y., Kimmel, R. & Zibulevsky, M. Conformal mapping with as uniform as possible conformal factor. SIAM J. Imag. Sci. 6, 78–101 (2013).
Stam, J. Nucleus: Towards a unified dynamics solver for computer graphics. Paper presented at the International Conference on Computer-Aided Design and Computer Graphics, Hong Kong (2009).
Cianchetti, M. et al. Soft robotics technologies to address shortcomings in today's minimally invasive surgery: the STIFF-FLOP approach. Soft Robo. 1 (2014).
Ryu, J. et al. Photo-origami – Bending and folding polymers with light. Appl. Phys. Lett. 100 (2012).
Otsuka, K. & Wayman, C. W. Shape Memory Materials. (Cambridge university press, 1999).
Jani, J. M., Leary, M., Subic, A. & Gibson, M. A. A review of Shape Memory Alloy research, applications and opportunities. Mater. Desig. (2013).
Wallce, G. G., Teasdale, P. R., Spinks, G. M. & AP, L. Kane-Maguire. Conductive electroactive polymers: intelligent polymer systems. (CRC Press, 2008).
Yi, S., Song, Y. S. & Paik, J. Characterization of silicone rubber based soft pneumatic actuators. Paper presented in the International conference on intelligent robots and systems, Tokyo (2013).
Ota, T. et al. A novel highly articulated robotic surgical system for cardiac ablation. Paper presented in the International Conference of IEEE Engineering in Medicine and Biology Society, Vancouver. (2008).
Author information
Authors and Affiliations
Contributions
This research was initiated by D.R, who also worked on the alignment of the shapes (before/after) and wrote most of the paper. W.Z., M.Z. and C.O. worked on the physical simulator, while C.M., A.P. and S.T. generated the digital models for printing and tested the physical models. S.H. and D.D. fabricated the models. A.K. and B.S. took active part in consulting, writing and data analysis. S.T. and R.R. overviewed this project.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Electronic supplementary material
Rights and permissions
This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivs 4.0 International License. The images or other third party material in this article are included in the article's Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder in order to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-nd/4.0/
About this article
Cite this article
Raviv, D., Zhao, W., McKnelly, C. et al. Active Printed Materials for Complex Self-Evolving Deformations. Sci Rep 4, 7422 (2014). https://doi.org/10.1038/srep07422
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep07422
This article is cited by
-
Relationship between programming stress and residual strain in FDM 4D printing
Progress in Additive Manufacturing (2024)
-
Rapid and selective actuation of 3D-printed shape-memory composites via microwave heating
Scientific Reports (2023)
-
Advancing cardiac regeneration through 3D bioprinting: methods, applications, and future directions
Heart Failure Reviews (2023)
-
Enhancing shape-recovery ratio of 4D printed polylactic acid (PLA) structures through processing parameter optimization
Progress in Additive Manufacturing (2023)
-
A critical review on 4D printing and their processing parameters
International Journal on Interactive Design and Manufacturing (IJIDeM) (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.


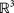 ) of this primitive by rotating the expanding and rigid strips with relation to the bars. This approach provides an additional degree of freedom in folding angles, as the plane in which the bars fold can also be controlled, as shown in
) of this primitive by rotating the expanding and rigid strips with relation to the bars. This approach provides an additional degree of freedom in folding angles, as the plane in which the bars fold can also be controlled, as shown in 
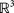 requires two degrees of freedom. One angle is achieved by changing the spaces between the inner disks, which provides a physical stop once the end angle is reached. The second angle is maintained by changing the angles in between two neighboring bars. One can consider it as a rotational shift that changes the plane in which the bars fold. (C) A complete example embedding dynamic primitives of stretching and folding on a grid. This grid can accommodate a self-evolving deformation into a complex structure with both convex and concave parts. (D) Calibration of the folding joints is performed by repeated experiments on a planar hexagon. See
requires two degrees of freedom. One angle is achieved by changing the spaces between the inner disks, which provides a physical stop once the end angle is reached. The second angle is maintained by changing the angles in between two neighboring bars. One can consider it as a rotational shift that changes the plane in which the bars fold. (C) A complete example embedding dynamic primitives of stretching and folding on a grid. This grid can accommodate a self-evolving deformation into a complex structure with both convex and concave parts. (D) Calibration of the folding joints is performed by repeated experiments on a planar hexagon. See 


