Abstract
Coherent Diffraction Imaging is a technique to study matter with nanometer-scale spatial resolution based on coherent illumination of the sample with hard X-ray, soft X-ray or extreme ultraviolet light delivered from synchrotrons or more recently X-ray Free-Electron Lasers. This robust technique simultaneously allows quantitative amplitude and phase contrast imaging. Laser-driven high harmonic generation XUV-sources allow table-top realizations. However, the low conversion efficiency of lab-based sources imposes either a large scale laser system or long exposure times, preventing many applications. Here we present a lensless imaging experiment combining a high numerical aperture (NA = 0.8) setup with a high average power fibre laser driven high harmonic source. The high flux and narrow-band harmonic line at 33.2 nm enables either sub-wavelength spatial resolution close to the Abbe limit (Δr = 0.8λ) for long exposure time, or sub-70 nm imaging in less than one second. The unprecedented high spatial resolution, compactness of the setup together with the real-time capability paves the way for a plethora of applications in fundamental and life sciences.
Similar content being viewed by others
Introduction
Novel short wavelength sources combined with lensless imaging methods such as coherent diffraction imaging (CDI) and others1 paved the way for microscopy with a resolution well below the wavelength of visible light. During the last decade we have witnessed a tremendous progress in the development of coherent extreme ultraviolet (XUV) and X-ray sources and their application to high-resolution imaging2,3,4. In CDI one directly collects the diffracted light with a large area CCD detector close to the sample, i.e. with a high numerical aperture. It thus holds promise for further improving the spatial resolution down to the atomic level. Most of the diffraction imaging experiments are carried out at large-scale facilities such as free-electron lasers and synchrotron sources. Limited access to these sources is a severe bottleneck for many applications. Laser driven high harmonic generation (HHG) sources allowed successful implementation of CDI at the lab scale5,6. However, typical HHG sources suffer from a low conversion efficiency and thus one either needs a large laser system for single-shot performance7,8,9 or relatively long exposure times10,11,12,13, which again renders broad usage of this technology, e.g., high resolution imaging in life sciences, difficult.
As mentioned above, an important prerequisite for high-resolution microscopy is an imaging system with a high numerical aperture (NA). However, for high NA imaging the temporal coherence of the light limits the achievable resolution in addition to the spatial coherence requirement that must be fulfilled for any NA. The smallest details of the sample can be only resolved if the diffraction pattern for large diffraction angles is recorded and evaluated. The diffraction pattern for large angles can be seen only if the coherence length is long enough, i.e. the relative bandwidth is small enough. In a recent publication Miao et al. presented an estimation of the resolution for a CDI experiment as a function of the relative bandwidth14

where O is the linear oversampling ratio, which should be a little larger than two in an experimental realization, a is the typical object size and Δλ/λ is the relative bandwidth of the illuminating light.
A closer inspection of Equ. (1) reveals a major limitation for the achievable resolution using HHG sources driven by ultrashort pulse lasers. For a high conversion efficiency the laser pulses must be of high intensity and the pulse duration must be as short as possible15. For typical Ti:sapphire laser systems the pulses are 30 fs or shorter, resulting in a rather large relative bandwidth. Consequently, the XUV light will also have a rather large relative bandwidth, which is typically on the order of Δλ/λ = 1/30. Using Equ. (1) the achievable resolution for a 3 micron large object can be estimated to be roughly 100 nm. Using longer driving pulses will lower the relative bandwidth, but at the same time reduces the conversion efficiency substantially. The lower photon flux will decrease the resolution by lowering the signal to noise ratio for a finite exposure time. Hence, the best ever reported relative spatial resolutions achieved with table-top CDI setups do not significantly reach below two wavelengths of the illuminating light7,11,16.
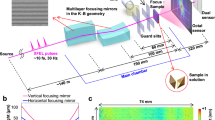
To overcome this limitation we employ an XUV source based on a high repetition rate ytterbium-doped fiber CPA system operating at 1030 nm wavelength with subsequent nonlinear compression in a xenon gas filled hollow core fiber17 (Fig. 1, methods). Our system is more compact than typically used ultrafast solid-state lasers, but the XUV photon flux is comparable or even higher18 due to the high repetition rate19. The fiber-based approach further ensures an excellent beam quality, which is essential for high NA imaging. Our setup also contains specially designed XUV multilayer mirrors for selecting a single narrow-bandwidth harmonic line and focusing the radiation onto the target to be imaged. To concentrate as much light as possible onto the target, we use two concave XUV mirrors, where the first collimates the generated XUV light and the second focusses the light onto the target. A narrow z-fold (α<3°) assures small aberrations. It is worth to mention that this approach using two concave mirrors relaxes the need for a single highly focussing mirror, consequently requiring steeper z-fold angles, in order to concentrate the light onto the target5 while the spectral selectivity is increased. The achieved focal spot size is roughly 5 µm (FWHM). The experimental setup along with a typical generated XUV spectrum featuring narrowband lines is depicted in Fig. 1. The XUV mirrors select the 31st harmonic of the IR laser leading to a monochromatic illumination with a relative bandwidth of Δλ/λ = 1/220 (λ = 33.2nm). See methods section for more experimental details. According to Equ. (1) the relative bandwidth allows for a resolution of Δr ≈ 26 nm, which is below the wavelength of the illuminating light.
The experimental setup for high resolution XUV imaging at high average power: (a), The pulses of a fiber based CPA (FCPA) system are spectrally broadened in a xenon filled hollow-core fiber and subsequently compressed with dielectric chirped mirrors (DCM). HHG is driven with 40 W of average power into a gas nozzle backed with 5 bar krypton. Two fused silica plates with antireflection coating for the IR are mainly reflecting the XUV light. Spectral selection of the 31st harmonic at 33.2 nm is done by a pair of aluminium filters followed by two curved XUV multilayer mirrors. The curved mirrors refocus the light tightly onto the sample. The diffracted light is captured by an XUV-sensitive CCD (CAM1). A beamstop (BS) suppresses the strong central speckle. (b) Measured XUV beam profile 20 mm behind the rear focus reveals good spatial beam properties. (c) The XUV multilayer mirrors, which are hit under almost normal incidence to minimize aberrations, have an overall reflectivity of 4.6% (solid black line) for the selected single harmonic line (dotted blue line).
For the high resolution imaging experiment we prepared a sample consisting of a 200 nm thick silicon nitride membrane covered with a 200 nm thick gold layer. With a focused ion beam we milled our institute's logo into the gold covered membrane forming a clear aperture with hard edges. A STEM image of the structure is depicted in Fig. 2a. The XUV radiation diffracted from the sample is captured in transmission geometry with an XUV sensitive CCD camera positioned 10 mm downstream from the sample. From the distance and the size of the camera chip we obtain a NA of 0.8. To suppress the high intensity central speckle of the diffraction pattern a beamstop was placed between the sample and the detector. It is worth mentioning that the whole setup, including the vacuum vessels used for HHG and imaging, is very compact and fits easily on an optical table. The Abbe limit for this configuration is Δr = 20 nm. Hence, considering the NA and the achieved bandwidth, ultrafast XUV CDI is possible for the first time with a resolution below the illuminating wavelength.
XUV diffraction pattern and reconstruction at 0.8λ resolution for 150 s exposure time: (a), STEM image of the sample consisting of a 200 nm gold layer on a 200 nm thick silicon nitride membrane. (b), Measured raw diffraction pattern for an exposure time of 150 s and 33.2 nm wavelength. The pixels which are overexposed or obscured by the beamstop are set to zero. (c), The reconstructed object space shows the non-periodic complex-shaped object. In this panel the phase and amplitude of the complex-valued object space is encoded in the hue and brightness, respectively. Only the sub-wavelength features (sparks on the right lower part in a and details in “Jena”) are missing as explained in the text (d), The analysis of the PRTF suggests a resolution of 26 nm corresponding to 0.8λ. The scale bars in a and c are one micron.
Results
The measured diffraction pattern for an exposure time of 150 s is shown in Fig. 2b. It covers the whole detector, implying the effective NA is comparable to the theoretical one. Prior to retrieving the object, the recorded image must be corrected, because the diffraction pattern will be projected onto the Ewald sphere and not onto the flat CCD chip16. After careful preparation of the experimental data we have successfully retrieved the object (Fig. 2c) using state-of-the-art phase retrieval techniques without any a priori knowledge except that the object is isolated, see methods section for details. The achieved spatial resolution is determined by analysing the phase retrieval transfer function (PRTF)20. Setting the threshold of the PRTF at 0.5 (Fig. 2d), which proofed to compare well with the achievable resolution in an optical microscope21, we obtain a half-period resolution of Δr = 26 nm. The strong drop of the PRTF at |q| ≈ 21 μm−1 is determined by the maximum observable momentum transfer, i.e. the measured intensity becomes too low, for an estimation of the PRTF. Nevertheless, up to |q| ≈ 19 μm−1 the observed speckles allow retrieving the phase reasonably well, justifying the claim of the quoted resolution. We are confident that determining the resolution by the PRTF as a general measure is more accurate considering possible soft edges generated in the fabrication process (see SI (S.1) for additional line profile analysis and further discussion). Note that the achieved resolution is below the wavelength of the illuminating light and compares to 0.8λ. This measured value is in excellent agreement with the estimate considering the temporal coherence of the used light pulses. However, a few of the sub-50 nm details, e.g. the sparks in the right lower part of the structure, are not visible in the reconstruction. We attribute this to a slight tilt of the object with respect to the propagation direction of the light. Due to the large aspect ratio (~30 nm width and 400 nm depth) already a slight tilt leads to obscuration of the light path, see SI (S.2) for a reconstruction of a different data set from a previous experimental run recorded at lower photon flux and thus lower effective NA. There, some features are visible which are not visible in Fig. 2c despite the overall resolution was lower. Hence, we are confident that the missing features can be attributed to the sample tilt.
For real world applications high spatial resolution is an essential feature, but equally important is the ability for real-time imaging, i.e. the exposure time should be in the order of one second or less without significantly reducing the resolution. Typical previously reported exposure times for reaching sub-100 nm resolution for compact HHG CDI setups range from 30 s (ref. 11) to several ten minutes10. Here, we recorded the diffraction pattern of the same sample with an exposure time of one second, whilst all other settings remained the same. From the raw data (Fig. 3a) we were able to reconstruct the image with good quality as shown in Fig. 3b. Despite the very short exposure time the photon flux was still sufficient to resolve the main features of the object. From the calculated PRTF (Fig. 3c) we have determined a half-period resolution of Δr = 65 nm, which is only two-times the wavelength of the illuminating light. With the present setup microscopic images with sub-100 nm resolution can be taken with a rate of one frame per second. Therefore, we were able to reduce the integration time for sub-100 nm resolution by one order of magnitude. We present reconstructions for different exposure times in the SI (SI.3). The bottle-neck for using this in an applied scheme is the phase retrieval process, which still takes minutes even on powerful computers. Nevertheless, there are applications where the diffraction pattern is directly assessed, e.g. the recently demonstrated CDI based cancer cell classification22.
Real-time XUV imaging at sub-70 nm spatial resolution: (a), Measured raw diffraction pattern using 1 s exposure time and 33.2 nm wavelength. The beamstop was removed for this measurement. The photon flux was sufficient to take full advantage of the dynamic range of the CCD. (b), Reconstructed object space (complex-value representation as in Fig. 2c) showing the main features of the nanostructured aperture. The scale bar is one micron. (c) The achieved spatial resolution according to the PRTF is Δr = 65 nm, which corresponds to roughly two wavelengths of the illuminating light.
Discussion
In conclusion, we demonstrated coherent diffractive imaging with sub-wavelength resolution by using a high repetition rate fibre laser based narrowband XUV source. The obtained resolution (Δr = 0.8λ) is the highest ever achieved resolution normalized to the wavelength for CDI regardless of the used source. Furthermore, this achievement demonstrates the high quality of the XUV beam and the unprecedented high degree of temporal coherence for a fiber laser driven HHG source. Moreover, the optical setup, including the laser, is much more compact than what is typically used for high resolution XUV CDI measurements and might soon allow implementing the presented technique even in portable setups. Furthermore, we demonstrated the capability of imaging sub-70 nm structures with an exposure time as short as one second, giving rise to a plethora of applications in real-time, time-resolved23 and multi-dimensional imaging24. Recent improvements of the average power per harmonic in the XUV now exceeding 100 µW per harmonic in FCPA driven HHG sources due to upscaling strategies18 or using several harmonic lines25 would significantly lower the exposure time further, allowing to use the full reported resolution in a real-time scheme. Along with the availability of different wavelengths in the harmonic frequency comb and the availability of a temporally highly correlated infrared laser this might open new possibilities in material and surface studies with wavelength-selective scattering. Further downscaling in the used wavelength towards the water window26 will allow the application in life science in the near future.
Methods
Experimental Setup
The driving laser system consists of an ytterbium-doped fiber chirped pulse amplifier and subsequent compression in a xenon filled hollow core fiber and is described elsewhere17. The 660 fs long pulses have an energy of about 350 µJ at a 200 kHz repetition rate. These pulses with an average power of 70 W are coupled into a hollow-core fiber with an inner diameter of 250 µm and a length of 1 m. The fiber is mounted on a water-cooled V-groove and is filled with xenon gas at about 1.5 bar of pressure. The pulses are spectrally broadened to an rms bandwidth of 40 nm and subsequently compressed to ~60 fs pulse duration with dielectric chirped mirrors. These temporally compressed 200 µJ pulses are focused into a krypton gas target that is supplied by a simple cylindrical nozzle having an opening of 250 µm. The intensity achieved in the focal spot is >1014 W/cm2. The jet is positioned slightly behind the focal spot, which results in a low divergence beam and a narrow spectral bandwidth, both of which is beneficial for imaging experiments. In addition, we optimize the backing pressure (~5 bar) and the opening of an iris placed in the collimated beam before the focusing optics in order to achieve the highest possible photon number in the 31st harmonic at ~37.3 eV or 33.2 nm wavelength, which is later selected by the XUV mirrors. We estimate the generated average power in the 31st harmonic to ~5 µW (8.4·1011 photons/s). A chicane made of two IR-antireflection coated fused silica plates operated under 82° angle of incidence helps to separate the pump and XUV radiation27. With additional aluminium filters (0.5 micron total thickness) we efficiently suppress parasitic remaining IR light which is also partially reflected by the subsequent XUV mirrors28. Further downstream a concave spherical multilayer mirror (f = 1 m) collimates a single harmonic line at 37.3 eV. The XUV beam is then focused onto the sample with a second concave XUV multilayer (f = 0.5 m) mirror. Both multilayer mirrors were produced with a dual ion beam sputtering system, described elsewhere29, generating a sequence of forty silicon/boron carbide layers on a spherical superpolished (roughness below 1 angstrom) fused silica substrate. Using two mirrors centred at the same wavelength enhances the spectral selectivity of the system approximately by a factor of  . While one mirror has a FWHM bandwidth of ~2.7 eV, the monochromatic characteristic can be increased to ~1.9 eV using a two mirror combination as spectral filter. A positive side-effect is the increased suppression (suppression factor > 20) of odd neighbour gas harmonics being spaced by ~2.4 eV at 1030 nm driving wavelength. To minimize aberrations we use both mirrors in a z-fold close to a normal incidence angle of 3°. The overall reflectivity of the two multilayer Bragg mirrors is 4.6 percent for s-polarisation.
. While one mirror has a FWHM bandwidth of ~2.7 eV, the monochromatic characteristic can be increased to ~1.9 eV using a two mirror combination as spectral filter. A positive side-effect is the increased suppression (suppression factor > 20) of odd neighbour gas harmonics being spaced by ~2.4 eV at 1030 nm driving wavelength. To minimize aberrations we use both mirrors in a z-fold close to a normal incidence angle of 3°. The overall reflectivity of the two multilayer Bragg mirrors is 4.6 percent for s-polarisation.
The diffraction pattern has been recorded with an XUV sensitive CCD camera (2048 × 2048 pixels, 13.5 × 13.5 µm pixel size). The XUV focal spot has an FWHM diameter of less than 5 µm, measured by scanning a 2 µm aperture across the beam profile in the focal plane. The few micron focal spot size is ideally suited to image single biologic specimen such as, e.g., breast cells with nanometer resolution while preserving a sufficiently large field-of-view22.
Image reconstruction
For the phase retrieval we employed a guided version30 of the RAAR algorithm31 (β−parameter varied between 0.8 and 0.7) without any a priori knowledge of the sample except that it is an isolated object. The shrink-wrap method32 was applied each 100 iterations to dynamically update the support, while an initial support was generated from the autocorrelation of the measured diffraction pattern with using locator sets for refinement33. The amplitude threshold used for shrinkwrap was set low and the applied Gaussian blurring was ramped from 10 to 1 pixel radius within 2000 iterations to allow slow shrinking of the support in order to avoid degradation of the fine features of the object. We started with ten independent reconstructions, enforcing positivity on each and iterated for 2000 steps. Then all reconstructions were averaged with the best of the reconstructions judged by the error metric34 for repeating the whole procedure until all reconstructions reached a stable solution. After 8 generations the individuals converged to a common solution. Pixels where no amplitude was measured (black pixels in Fig. 2b) were allowed to evolve freely in amplitude and phase32. For the pixels outside a circle representing ~21 µm−1, i.e. the very high diffraction angles, where no regular speckles were measured, additionally an amplitude threshold corresponding to the amplitude of the weakest measured speckles was enforced.
References
Chapman, H. N. & Nugent, K. A. Coherent lensless X-ray imaging. Nature Photon. 4, 833–839 (2010).
Jiang, H. et al. Quantitative 3D imaging of whole, unstained cells by using X-ray diffraction microscopy. Proc. Natl. Acad. Sci. USA 107, 11234–11239 (2010).
Barty, A. et al. Ultrafast single-shot diffraction imaging of nanoscale dynamics. Nature Photon. 2, 415–419 (2008).
Mancuso, A. P. et al. Coherent imaging of biological samples with femtosecond pulses at the free-electron laser FLASH. New. J. Phys. 12, 035003 (2010).
Sandberg, R. L. et al. Lensless diffractive imaging using tabletop coherent high-harmonic soft-x-ray beams. Phys. Rev. Lett. 99, 098103 (2007).
Zuerch, M., Kern, C. & Spielmann, C. XUV coherent diffraction imaging in reflection geometry with low numerical aperture. Opt. Express 21, 21131–21147 (2013).
Ravasio, A. et al. Single-shot diffractive imaging with a table-top femtosecond soft x-ray laser-harmonics source. Phys. Rev. Lett. 103, 028104 (2009).
Schwenke, J. et al. Single-shot holography using high-order harmonics. J. Mod. Opt. 55, 2723–2730 (2008).
Ge, X. et al. Impact of wave front and coherence optimization in coherent diffractive imaging. Opt. Express 21, 11441–11447 (2013).
Sandberg, R. L. et al. Tabletop soft-X-ray Fourier transform holography with 50 nm resolution. Opt. Lett. 34, 1618–1620 (2009).
Seaberg, M. D. et al. Ultrahigh 22 nm resolution coherent diffractive imaging using a desktop 13 nm high harmonic source. Opt. Express 19, 22470–22479 (2011).
Chen, B. et al. Multiple wavelength diffractive imaging. Phys. Rev. A 79, 023809 (2009).
Sandberg, R. L., Huang, Z., Xu, R., Rodriguez, J. A. & Miao, J. Studies of Materials at the Nanometer Scale Using Coherent X-Ray Diffraction Imaging. J. Microsc. 65, 1208–1220 (2013).
Miao, J., Ishikawa, T., Anderson, E. H. & Hodgson, K. O. Phase retrieval of diffraction patterns from noncrystalline samples using the oversampling method. Phys. Rev. B 67, 174104 (2003).
Brabec, T. & Krausz, F. Intense few-cycle laser fields: Frontiers of nonlinear optics. Rev. Mod. Phys. 72, 545–591 (2000).
Raines, K. S. et al. Three-dimensional structure determination from a single view. Nature 463, 214–217 (2010).
Rothhardt, J. et al. 1 MHz repetition rate hollow fiber pulse compression to sub-100-fs duration at 100 W average power. Opt. Lett. 36, 4605–4607 (2011).
Hädrich, S. et al. High photon flux table-top coherent extreme-ultraviolet source. Nat. Phot. 8, 779–783 (2014).
Heyl, C. M., Güdde, J., L'Huillier, A. & Höfer, U. High-order harmonic generation with μJ laser pulses at high repetition rates. J. Phys. B: At. Mol. Opt. Phys. 45, 074020 (2012).
Chapman, H. N. et al. High-resolution ab initio three-dimensional x-ray diffraction microscopy. J. Opt. Soc. Am. A Opt. Image Sci. Vis. 23, 1179–1200 (2006).
Shapiro, D. et al. Biological imaging by soft x-ray diffraction microscopy. Proc. Natl. Acad. Sci. USA 102, 15343–15346 (2005).
Zürch, M. et al. Cancer cell classification with coherent diffraction imaging using an extreme ultraviolet radiation source. J. Med. Imag. 1, 031008 (2014).
Wieland, M. et al. Toward time-resolved soft X-ray microscopy using pulsed fs-high-harmonic radiation. Ultramicroscopy 102, 93–100 (2005).
Praeger, M. et al. Spatially resolved soft X-ray spectrometry from single-image diffraction. Nat. Phys. 3, 176–179 (2007).
Parsons, A. D. et al. Ultra-broadband support determination for extreme ultraviolet coherent diffractive imaging from a high harmonic source. J. Opt. 15, 094009 (2013).
Rothhardt, J. et al. 53 W average power few-cycle fiber laser system generating soft x rays up to the water window. Opt. Lett. 39, 5224–5227 (2014).
Pronin, O. et al. Ultrabroadband efficient intracavity XUV output coupler. Opt. Express 19, 10232–10240 (2011).
Hofstetter, M. et al. Attosecond dispersion control by extreme ultraviolet multilayer mirrors. Opt. Express 19, 1767–1776 (2011).
Guggenmos, A. et al. Aperiodic CrSc multilayer mirrors for attosecond water window pulses. Opt. Express 21, 21728–21740 (2013).
Miao, J. et al. Three-Dimensional GaN-Ga2O3 Core Shell Structure Revealed by X-Ray Diffraction Microscopy. Phys. Rev. Lett. 97, 215503 (2006).
Luke, D. R. Relaxed averaged alternating reflections for diffraction imaging. Inverse Probl. 21, 37–50 (2005).
Marchesini, S. et al. X-ray image reconstruction from a diffraction pattern alone. Phys. Rev. B 68, 140101 (2003).
Fienup, J. R., Crimmins, T. R. & Holsztynski, W. Reconstruction of the Support of an Object from the Support of Its Auto-Correlation. J. Opt. Soc. Am. 72, 610–624 (1982).
Miao, J., Sayre, D. & Chapman, H. N. Phase retrieval from the magnitude of the Fourier transforms of nonperiodic objects. J. Opt. Soc. Am. A 15, 1662–1669 (1998).
Acknowledgements
Support from European Regional Development Fund (EFRE) and TMBWK under grant number B 715-08008 is acknowledged. S. Wolf of the Institute for Solid State Physics is acknowledged for fabricating the sample. This work has been partly supported by the German Federal Ministry of Education and Research (BMBF) and the European Research Council under the European Union's Seventh Framework Programme (FP7/2007-2013)/ERC Grant agreement n° [240460]. The XUV multilayer development has been supported by the DFG excellence cluster Munich Centre for Advanced Photonics (MAP).
Author information
Authors and Affiliations
Contributions
M.Z. planned, built and optimized the CDI setup. J.R., S.H., S.D., M.K. and J.L. built and optimized the FCPA and HHG setup. M.Z. and J.R. conducted the experiments. A.G. and U.K. designed and fabricated the XUV multilayer mirrors. M.Z. performed the reconstructions and evaluated the experimental data. M.Z., J.R., J.L., A.T. and C.S. planned and initiated the project. All authors contributed to the manuscript.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Electronic supplementary material
Supplementary Information
Supplementary Information
Rights and permissions
This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivs 4.0 International License. The images or other third party material in this article are included in the article's Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder in order to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-nd/4.0/
About this article
Cite this article
Zürch, M., Rothhardt, J., Hädrich, S. et al. Real-time and Sub-wavelength Ultrafast Coherent Diffraction Imaging in the Extreme Ultraviolet. Sci Rep 4, 7356 (2014). https://doi.org/10.1038/srep07356
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep07356
This article is cited by
-
How to optimize high-order harmonic generation in gases
Nature Reviews Physics (2022)
-
Photon counting of extreme ultraviolet high harmonics using a superconducting nanowire single-photon detector
Applied Physics B (2022)
-
Electron quantum path control in high harmonic generation via chirp variation of strong laser pulses
Scientific Reports (2021)
-
Divergence and efficiency optimization in polarization-controlled two-color high-harmonic generation
Scientific Reports (2021)
-
Coherent Tabletop EUV Ptychography of Nanopatterns
Scientific Reports (2018)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.