Introduction

“Orthogonality” is a term borrowed from geometry: if two straight lines intersect at right angles, they are orthogonal: i.e., mutually independent. The projection of a vector representing movement along a straight line onto an orthogonal line will be a single point. Orthogonality plays a fundamental role in Banach spaces and various definitions of orthogonality in this context have been introduced since 19341,2, such as the orthogonalities of Roberts, Birkhoff, James, Carlsson, Diminnie and Alonso. In physics, operator theories state that the eigenfunctions corresponding to different eigenvalues of the same Hermitian operator are orthogonal to each other. Orthogonality makes the analysis and control of physical phenomena extremely convenient3,4. In a straight waveguide (see the Supplementary Material), the guided wave modes, which are represented by different transverse standing waves, are mutually orthogonal and do not couple with each other during propagation. Each transverse mode in a cylindrical waveguide corresponds to Bessel function distributions of different standing waves, which have applications in various fields beyond acoustics. Bessel function acoustic pressure fields generated using a multi-focus Fresnel lens5 and a circular ultrasound array6 have been used to trap and control microparticles. Optical tweezers formed using a single Bessel beam instead of Gaussian beams can be used to trap particles in multiple spatially separated sample cells7. To achieve control of optically bound structures, Bessel laser modes have been produced using a spatial light modulator8. In virtual ghost imaging, the use of Bessel-beam illumination instead of Gaussian illumination has been demonstrated to produce an image in both clear- and turbulent-air experiments9. Because of their small focal spots, Bessel beams have also been used in femtosecond-laser nanofabrication10,11. However, single-mode generation is always both complicated and expensive. Here, we introduce a waveguide in which a section with periodically perturbed walls interfaces with a smooth section to generate a single pure high-order mode. In the periodic section, the orthogonality of the eigenmodes of the smooth waveguide section is destroyed and the energy is redistributed among the modes. The resulting complex interferences among the transverse modes are highly promising for the generation of a single high-order mode with a carefully selected periodicity.

Periodic structures have been extensively investigated since the pioneering work of Lord Rayleigh12 in 1887. More detailed theories and applications can be found in Elachi's review13 and the references therein. In past decades, wave propagation in waveguides with corrugated walls has also been extensively investigated. In 1974, Nayfeh14 employed the multiple-scale method to investigate the sound resonances in a duct with small wall corrugations. Boström15 and Standström16 have used the null-field method to analyse the band structures of cylindrical and planar waveguides, respectively. El-Bahrawy17 has studied the Rayleigh-Lamb modes in a plate with sinusoidally corrugated walls. In 2006, Banerjee and Kundu theoretically developed generalised dispersion equations18 and experimentally investigated wave propagation19 in corrugated plates. With the development of concepts such as negative refraction20,21, thermal management22 and invisibility cloaking23, the behaviour of waves in periodic structures has attracted considerable interest in the context of so-called photonic crystals in optics and phononic crystals in acoustics24,25,26,27,28. The creation of forbidden bands is attributed to the well-known Bragg resonances, which are induced by the strong interference between two oppositely propagating waves with identical transverse wave fronts in a periodic waveguide. When the transverse dimensions of the waveguide increase, higher-order transverse modes arise in addition to the fundamental mode and so-called non-Bragg resonances occur because of the coupling of waves with different wave fronts29,30,31. In 2008, Tao et al. developed a graphical method32 of addressing two-mode resonances, in which the guided wave modes are represented by lines in the first Brillouin zone and resonances occur at the intersections of these lines. All of these lines depend on the wall period and changing the period results in different diagrams in the first Brillouin zone. The smaller the period is, the more transverse modes are involved. Using this method, three-mode resonances were theoretically and numerically investigated in a sinusoidal wall duct in a study conducted in 201433. When the periodicity of the wall corrugations is carefully chosen, it is possible for all but one of the transverse modes to be reflected. Such an orthogonality-breaking system will effectively behave as a “higher-mode generator”.

Results

Orthogonality and orthogonality breaking

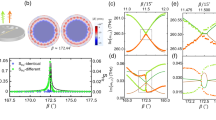
When sound propagates in a straight waveguide that is filled with a perfect gas and consists of rigid walls, the number of propagating modes depends on the incident frequency. Figure 1 (a) shows transverse standing waves propagating through a straight waveguide with rigid walls. On the left are the incident waves, on the right are the output waves and the rigid duct is depicted in the middle. The mode diagram consists of the transverse distributions and their longitudinal wavenumbers. The green, black and red arrows denote the longitudinal wavenumbers of the fundamental, first and second modes, respectively. The small images above the arrows depict the field distributions of the different transverse modes. When the working frequency is f, the transverse (kt,m) and longitudinal (kl,m) wavenumbers for the mth mode satisfy the following dispersion relation with the speed of sound c:

Figure 1
figure 1

Mode diagram for orthogonality and orthogonality breaking.

The green, black and red arrows denote the longitudinal wavenumbers of the fundamental, first and second modes, respectively. The length of each arrow indicates the magnitude of the corresponding wavenumber. The small images above the arrows depict the field distributions of the different transverse modes at the cross section. The vertical ordinate represents the frequency. f1 and f2 are the cutoffs for the first and second modes, respectively and the purple cylinders represent the investigated waveguide. The purple lines indicate the wavenumbers of the periodic corrugations. (a) No interference occurs among the different modes in a straight duct because of their orthogonality. The left-hand side shows the incident waves and the right-hand side depicts the output waves. (b) Mode-interaction diagram for orthogonality breaking: incident fundamental modes (left) and mode interactions in the periodic waveguide (right). (c) A three-mode interaction to induce single-mode transparency: two-mode interaction diagrams (left), the interaction-coupling process (middle) and the interaction diagram of the fundamental mode, the first mode and the single remaining second mode (right).

Full size image

The vertical ordinate represents the frequency and f1 and f2 are the cutoffs for the first and second modes, respectively. From Fig. 1 (a), we observe that only the fundamental mode can propagate through the waveguide when the incident frequency is smaller than the first cutoff. Increasing the incident frequency will result in more transverse modes, which are mutually orthogonal and do not interact with each other. Thus, different transverse standing waves will pass independently through the waveguide. The output transverse modes exactly match the input transverse modes. The longitudinal wavenumber of each transverse mode increases as the frequency increases. Because of the orthogonality of the transverse modes, the incident waves must consist of different transverse-mode distributions. If there were only one mode incident on the duct, then the output would consist only of this mode, regardless of the working frequency. However, when the incident transverse distributions are not controlled, the number of excited modes is solely determined by the working frequency. When the frequency is higher than f1 or f2, then two or three modes, respectively, will propagate through the straight duct. At a constant frequency, the longitudinal wavenumber will decrease from the fundamental mode to the second mode as the transverse wavenumber increases. A larger transverse wavenumber corresponds to more transverse fluctuations, as illustrated in the mode diagrams. The diagrams are markedly different for the first three modes in the duct.

When we introduce periodically varying walls into the duct, as indicated in the middle of Fig. 1 (b) by purple cylinders, the orthogonality is broken and thus, the mode situation changes such that all formerly orthogonal modes will couple with one another and, regardless of the type of incident wave, the transverse modes will be excited in a manner dependent on the working frequency. The left-hand side of the figure depicts incident waves with increasing longitudinal wavenumbers. The transverse distributions are simply selected to correspond to the fundamental mode because this mode will create higher-order modes in the waveguide when it interacts with the corrugated walls. The wavenumber of the wall, (where Λ is the wall period), is also represented by the purple line under the purple waveguide. The right-hand side of the image illustrates the mode interactions in the waveguide. When the working frequency is lower than f1, the high-order modes are not excited. The longitudinal wavenumber of the fundamental mode is . The reflections from the corrugated walls give rise to a fundamental mode travelling in the opposite direction with longitudinal wavenumber −kl,0. When the sum of the two wavenumbers (two green arrows) reaches the wall wavenumber (the purple line), a traditional Bragg resonance arises, in which the reflections are enhanced and the strong interference between the incident and reflected waves results in a Bragg bandgap in the frequency domain. The Bragg resonance condition is also clearly indicated by the mode diagram. When the frequency is above the first cutoff, the corrugated wall produces a reflected first mode with longitudinal and transverse wavenumbers of kl,1 and kt,1, respectively. kl,1 is indicated by a black arrow in the figure. When the length of the connected black and green arrows is equal to the length of the purple line, non-Bragg resonance arises and creates a non-Bragg gap. The difference between the Bragg and non-Bragg resonances is also clearly demonstrated by the diagrams, which indicate whether the transverse modes involved in the interactions are identical. Because the incident frequency is far from the resonances, the waveguide becomes transparent once more, but multiple propagating modes arise because of the orthogonality breaking.

We introduce these mode diagrams to analyse the resonances in the waveguide. In addition to the examples presented in Fig. 1 (b), several diagrams can be presented that display various mode interactions. Figure 1 (c) shows an intriguing manipulation of mode interactions that gives rise to single-mode transparency in the waveguide. First, we consider the two-mode interactions among the first three modes (see the Supplementary Material). When the frequency is larger than the second cutoff, multi-mode interference will occur. As previously mentioned, we can identify two non-Bragg resonances, such as those on the left-hand side of Fig. 1 (c), which represent the interactions between the fundamental and second modes (upper) and between the first and second modes (lower). We can obtain identical red arrows in the two diagrams by properly selecting the wall wavenumber (the purple line) and the incident frequency (which affects the lengths of the arrows). When we combine these two resonances in the middle of the figure and shift the upper or lower modes by the length of the red arrows, as shown in the right-hand portion of the figure, we find that the second mode does not interact with the resonance of the first two modes. Based on the proposed mode diagrams, we strongly believe that orthogonality breaking is a highly promising approach to single high-order mode generation and lower-mode suppression.

The bandgap and its transparency

As shown in Fig. 2 (a), the orthogonality-breaking waveguide consists of a stainless steel pipe with alternating inner diameters of 100 and 125 mm. The corresponding axial widths are 27.5 and 26 mm, respectively, such that the spatial period is Λ = 53.5 mm. There are ten periods in this finite waveguide. The pipe wall is 4 mm thick and can be treated as a rigid boundary in the investigated frequency range. The experimental set-up is also illustrated schematically in Fig. 2 (a). Using our previously proposed graphical method32, the orthogonality-breaking waveguide can be regarded as a duct with multi-mode interactions, which are interpreted using a series of lines:

where r0 is the mean radius of the corrugated waveguide, β is the propagation constant and kr,m( = kt,mr0) is a zero of the first-order Bessel function. The first zero of the first-order Bessel function is zero, so the fundamental mode has a vanishing transverse wavenumber, as represented by a plane in Fig. 1. We denote the subsequent modes as the first, the second, etc. The line indicates the characteristics of the mth mode of the nth spatial harmonic. Figure 2 (b) illustrates the three-mode interaction of the pipe and its induced passband for a single transverse mode in the first Brillouin zone. The solid red line represents the second mode of the zeroth harmonic, whereas the green dash-dotted lines represent the fundamental mode and the black dashed lines represent the first mode of the ±1 st harmonics. Each line intersection corresponds to a resonance, which causes the dispersion curves to repel each other. For our steel pipe, the intersections among the solid, dashed and dash-dotted lines are remarkably close to each other. The typical two-mode interactions will become three-mode interactions and the second-order mode will stand away from the other two modes through a slightly different interaction mechanism, as shown in Fig. 1 (c). Hence, there will be second-mode transmission in the bandgaps of the fundamental and first modes. The blue dots in Fig. 2 (b) constitute dispersion curves computed based on Floquet theory32. These dots represent the propagating modes in the waveguide. No sound can pass through the pipe when the incident frequency deviates from these dots. Using the lines that correspond to the different modes, we can identify the modes that create the spectral structures. In the stopband, a narrow passband appears at approximately 6600 Hz to 7000 Hz. In the passband, the blue dots lie near the solid red line, especially near the centre of the Brillouin zone, which indicates that the extraordinary transmission of the single second-order mode is induced by the orthogonality breaking.

Figure 2
figure 2

Elaborate waveguide with orthogonality-breaking structures.

(a) Schematic illustration of the experimental set-up. A diameter-modulated stainless steel pipe is shown in the upper inset. The symmetric sound waves were regulated to low-order transverse modes, propagated through the structured waveguide and were detected by a microphone housed in a long tube. (b) Multi-mode interactions between the fundamental (green dash-dotted lines), first (black dashed lines) and second (solid red line) modes as well as the dispersion curves of the structured waveguide (blue dots). (c) Sound transmission exhibiting extraordinary transparency in the forbidden band. The solid red line represents the measured axial transmission and the blue dashed line represents the calculated power transmission.

Full size image

In the experiment, we swept the frequency from 6000 Hz to 7500 Hz. The axial transmission is represented in Fig. 2 (c) by a solid line. The transmission rapidly decreased at approximately 6300 Hz, began to increase at 6600 Hz, decreased again near 7000 Hz and increased once more above 7300 Hz. The solid line reveals a clear stopband from 6300 Hz to 7300 Hz and evidence of transmission in this band at approximately 6600–7000 Hz. Simple tests for axial transmission indicated that the data recorded along the axis were sufficient to reveal extraordinary transmission in the forbidden band. For comparison, the sound power transmission of the periodic duct was calculated using the finite-element method and the results are indicated in Fig. 2 (c) by a dashed line. More distinctly, there was additional transmission in the bandgap. Based on our theoretical analysis, we conclude that the transmission at approximately 6600–7000 Hz originated from the single second-order transverse mode, whereas the bandgap was dominated by the fundamental and first-order modes.

First and second modes

Another experiment was conducted to confirm the radial distributions of sound pressure in the ducts to investigate the bandgap. According to the axial transmission, we radiated sound waves into the corrugated pipe at frequencies of 6295 and 7320 Hz, corresponding to the lower and upper boundaries of the stopband, respectively. The frequencies were selected to ensure that the axial transmission was identical to that at the peak of the passband while preventing the sound pressure from being too weak to be detected. Then, we placed the microphone into the straight duct on the right-hand side, as shown in Fig. 2 (a). We recorded the sound pressure while moving the translation stage along the symmetry axis and found that the maximum sound pressure occurred near z = 350 mm based on the coordinates shown in Fig. 2 (a). The starting point of the microphone was the origin of the coordinate system; the z axis ran from right to left along the symmetry axis and the x axis was perpendicular to the z axis. At z = 350 mm, we moved the microphone along the x axis from 0 to 45 mm and recorded the sound pressure at 1-mm intervals for each frequency. Figure 3 (a) presents the measured sound pressure data for 6295 Hz (top circles) and 7320 Hz (bottom circles), with each data series normalised to its own maximum value. To identify the wave modes of the distributions, we also performed a least-square fit to the measured data using a truncated model:

where the sum of squares was minimised over coefficients am with a normalisation of , J0(·) is the zeroth-order Bessel function and the radius R was fixed to 50 mm in the fit. The optimal coefficients for each mode are provided in Table I and the best-fit curves are represented in Fig. 3 (a) by solid lines. The fitting results indicate that the fundamental and first modes were the major components of the distributions at the lower and upper edges of the bandgap, whereas the second mode provided a very small contribution. The fitted value of a3 is sufficiently small to support the truncation of the fitting model. The fitting results confirm our theoretical analysis of the origin of the bandgap, namely, that the fundamental and first modes dominate the stopband, although the second mode demonstrates some participation in the resonance.

Table 1 Optimal parameters of the best-fit curves for frequencies at the edge of the forbidden band
Full size table
Figure 3
figure 3

Transverse distributions: (a) Measured radial distributions of the sound pressure (circles) and their best-fit curves (solid lines) for 6295 Hz and 7320 Hz. Each measured data series is normalised to its own maximum value. (b) Sound pressure along the diameter in the corrugated waveguide (top) and in the straight duct (bottom) for 6910 Hz. The circles represent the measured pressures normalised to the maximum values of their corresponding data series and the solid lines represent the theoretical distributions of the second and first modes in the top and bottom portions, respectively.

Full size image

Finally, we examined the second-mode transparency. Although the bandgap is produced by the lower modes, does the transmission actually consist of the single high-order mode, without any interference from the other modes? To answer this question, we set the incident sound frequency to 6910 Hz, where the axial transmission reaches its maximum in the passband. First, we moved the microphone along the z axis to search for the maximum sound pressure. When the microphone was swept through the right part of the orthogonality-breaking pipe, we observed the maximum pressure at z = 651 mm. With the longitudinal position fixed at this maximum pressure, the microphone was then moved from −45 to 45 mm along the x axis. The recorded data were normalised to their maximum value and the results are presented in the top portion of Fig. 3 (b) as circles. In addition, the norm of the analytical Bessel function of the second mode, J0(kr,2r/R), is represented by a solid line. Because the location of the microphone at z = 651 mm corresponded to the wide region of the pipe, we choose R to be 62.5 mm. The trend observed in the recorded data was consistent with the analytical results, except near the pipe wall. This discrepancy can be easily explained by the fact that it was necessary to place the microphone, with its 10-mm-diameter support, near a relatively small chamber (26 mm × 12.5 mm) to sense the small amplitude of the sound pressure (see the Supplementary Material). The resulting multiple reflections enhanced the received signals and obscured the existence of low sound pressures near the wall. Because of this deviation, we could not perform the fit as previously described. However, comparison between the theoretical and experimental data indicates that the expected single second transverse mode did, indeed, appear, particularly when we read out the wave nodes near the theoretically predicted locations. The experimental results confirm the theoretical prediction of extraordinary second-order mode transparency. Thus, in an orthogonality-breaking pipe, we can manipulate the wave front by means of multi-mode interactions. Furthermore, we investigated the transverse distribution in the straight duct on the right-hand side and unexpectedly obtained a pure first mode. The corresponding normalised pressure and Bessel function are presented in the bottom portion of Fig. 3 (b) as circles and a solid line with the radius of the straight duct (R = 50 mm), respectively. The measured data were consistent with the Bessel function, indicating that using the proposed structure, we can achieve pure first and second modes.

Discussion

In summary, we propose a periodic waveguide structure that can break the orthogonality of the transverse wave modes and give rise to extraordinary transparency of a high-order transverse mode in a lower-mode forbidden band. The eigenmodes of cylindrical waveguides indicate that the transparent modes are Bessel function distributions with different nodes. By fabricating waveguides based on guidance from the mode diagrams, we can obtain many functional devices for various applications. The corrugated stainless steel waveguide employed herein exhibited three-mode interactions and yielded two types of Bessel function distributions, which could be applicable in optical and acoustical tweezers, microparticle trapping, the boundary control of soft matter, imaging, nanofabrication, etc. Moreover, the concepts of an orthogonality-breaking structure and the single-mode generation mechanism can be extended to higher-order modes to obtain Bessel-like distributions with more nodes. Although the experiment was conducted using an acoustic waveguide, we believe that analogous effects will also be observed in various fields, such as ultrasonics, optics, microwaves, terahertz waves, because of the ubiquity of wave phenomena.

Methods

Structure preparation

We fabricated the orthogonality-breaking waveguide using 4-mm-thick stainless steel materials, including a plate and two pipes, one with an inner diameter of 100 mm and the other with an inner diameter of 125 mm. First, we lathed the wide and narrow pipes into 26-mm-long and 27.5-mm-long pieces, respectively. Second, we machined the plate into flanges with an inner diameter of 108 mm and an outer diameter of 125 mm. Finally, the pipe sections were welded to the flanges.

Experimental set-up and measurements

Figure 2 (a) depicts the experimental set-up, in which a harmonic signal was generated by a National Instruments PCI-4461 card interfaced with a computer and was then magnified by an amplifier. The signal subsequently excited the coaxial monitor speaker to radiate axially symmetric sound waves into a 500-mm-long straight duct with a diameter of 100 mm. The incident sound waves could be effectively regulated to consist only of low-order transverse modes; complex high-order modes were removed by the cutoffs of the straight duct. Thus, we could guarantee the simplicity of the wave structures entering the orthogonality-breaking pipe. At the end of the periodic duct, another straight duct was attached to establish the output impedance. A microphone (G.R.A.S. 1/4″ free-field microphone 46BE) was placed into a 2-m-long stainless steel pipe with an outer diameter of 10 mm, which was mounted on a 3-dimensional motorised translation stage, to allow for the detection of sound pressure fields throughout most of the corrugated duct. The signals received by the microphone were sampled at 200 kHz and were recorded by the PCI card at its input port. A tone-extraction analysis was performed to determine the frequency and amplitude of the obtained sound waves. In a typical experiment, we created a sinusoidal signal using the Labview Signal Express software provided with the PCI card, which excited the speaker to radiate monochromatic sound waves into the ducts. The outlet and inlet sound pressure amplitudes were recorded at select positions along the axes of the two straight ducts and the axial transmission could be calculated from their ratio.

Numerical calculations

FEM simulations of acoustic pressure fields were performed using COMSOL Multiphysics with an axisymmetric model (see the Supplementary Material). The acoustic properties in the simulation domains were set as follows: a density of 1.25 kg/m3 and a sound speed of 343 m/s (in air). Plane-wave radiation boundary conditions were assigned to the inlet and outlet boundaries of the waveguide and hard-boundary sound conditions were selected for the outer boundaries. The frequency of the incident plane wave was varied from 6000 Hz to 7500 Hz with a step size of 1 Hz. The incident and transmitted sound powers were calculated using the boundary integration tool.