Abstract
In LaTiO3/SrTiO3 and LaAlO3/SrTiO3 heterostructures, the bending of the SrTiO3 conduction band at the interface forms a quantum well that contains a superconducting two-dimensional electron gas (2-DEG). Its carrier density and electronic properties, such as superconductivity and Rashba spin-orbit coupling can be controlled by electrostatic gating. In this article we show that the Fermi energy lies intrinsically near the top of the quantum well. Beyond a filling threshold, electrons added by electrostatic gating escape from the well, hence limiting the possibility to reach a highly-doped regime. This leads to an irreversible doping regime where all the electronic properties of the 2-DEG, such as its resistivity and its superconducting transition temperature, saturate. The escape mechanism can be described by the simple analytical model we propose.
Similar content being viewed by others
Introduction
Two-dimensional electron gases (2-DEGs) at LaAlO3/SrTiO3 and LaTiO3/SrTiO3 oxide interfaces1 have attracted much attention since their electronic properties display a very rich physics with various electronic orders such as superconductivity2,3,4 and magnetism5,6,7,8. In these structures, the 2-DEG is confined in an interfacial quantum well that typically extends on the order of 10 nm into the SrTiO3 substrate at low temperature2,4,9,10,11. Applying a back-gate voltage enables to control electrostatically the filling of the well and thus modulate the 2-DEG electronic properties12,13,14. This exciting feature opens new avenues for studying the electronic orders and quantum phase transitions15 in theses structures, as well as for developing oxide-based electronics that could make use of them16,17,18,19. Of particular interest, it was shown that adding electron to the well, increases continuously the electronic mobility and the strength of the Rashba spin-orbit coupling14,20,21. Also of interest, is the fact that the superconducting transition temperature of the 2-DEG exhibits a dome-like shape with a maximum Tc of 200–300 mK at optimal doping13,14. Because of these remarkable properties, the highly-doped regime must be explored in further detail. However, the overdoped side of the dome seems particularly difficult to study because of unexplained saturation and hysteresis of the physical properties13,14,20. As of yet, this region is not fully understood. These observations raise a fundamental question: how much one can electrostatically dope the 2-DEG at oxides interfaces?
Although several theoretical descriptions of LaXO3(X = Al, Ti)/SrTiO3 interfaces have been proposed22,23,24,25,26,27, the exact interfacial band structure remains controversial. Regardless of the calculation method and for the sake of clarity, in the present report we will consider a simple generalized situation where the bending of the SrTiO3 conduction band defines a quantum well that accommodates discrete electronic sub-bands. To illustrate this point, we show in the Figure 1 the type of result that can be obtained by using a semiconductor approach in which we solve self-consistent Schrödinger-Poisson equations14,28. In this example, six sub-bands are filled and the higher energy one extends within 5 nm in the SrTiO310,11; this situation corresponds to a carrier density of approximately 7 × 1013 e−/cm2, typical of values found in the literature. The effect of a back gate voltage on the interface is twofold: (i) it adds electrons to the well as the gate voltage increases (ΔVG > 0) and removes electrons from the well as the gate voltage decreases (ΔVG < 0), (ii) it controls the shape of the upper part of the well by tilting the conduction band profile in the substrate. Figure 2 shows illustrations of quantum well energy profiles that describe these different situations. As long as the Fermi level remains deep in the well, electrostatic gating can reversibly empty and fill the well as in the well-known semiconductors quantum wells. However, when the Fermi level rises to the top of the well, we no longer expect the doping to be possible. In this article we show that in LaXO3(X = Al, Ti)/SrTiO3 heterostructures, the Fermi energy lies intrinsically near the top of the well and that, beyond a filling threshold, additional electrons irreversibly escape from the well, hence limiting the possibility to reach a highly-doped regime. This behaviour can be described by a simple analytical model based on a thermal activated mechanism.
(a) Theoretical calculation of the quantum well profile at an LaXO3(X = Al, Ti)/SrTiO3 interface for a sample with a carrier density of 7.3 × 1013 e−/cm2. Shown are the SrTiO3 conduction band profile EC (black), the Fermi energy EF (blue dashed line) and the subbands energies (red) as a function of depth z from the interface. Only light dxy electron bands have been taken into account to illustrate the quantum well (see Model and Discussion part for more details). The square modulus of the envelope function of the first and last filled sub-bands are indicated in arbitrary units (red areas). (b) and inset of panel (a): Schematic description of the crystallographic structure at interface.
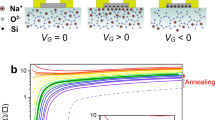
(a) Schematic of an LaXO3(X = Al, Ti)/SrTiO3 sample with a metallic back gate. (b,c,d) Illustration of filling the quantum well for different VG regimes. Starting from VG = 0, applying a negative gate voltages VG < 0 reversibly empties and fills the well. In contrast, applying the first positive polarisation (VG > 0), causes electrons to irreversibly escape from the well. The slope −eVG/d (where d = 500 μm is the thickness of the SrTiO3 substrate) of the conduction band is indicated.
Results
First positive polarization
In these experiments we used LaTiO3 and LaAlO3 epitaxial layers grown on TiO2-terminated SrTiO3 single crystals by Pulsed Laser Deposition as described in the Methods section. The samples had typical dimensions of 1 × 2 mm2 and each had a metallic back-gate deposited at the rear of the 0.5 mm thick SrTiO3 substrate. Before cooling, samples are kept in the dark for more than twelve hours to suppress any photoconductive effects. We studied the transport properties of LaXO3(X = Al, Ti)/SrTiO3 heterostructures at 4.2 K while applying a positive gate voltage for the first time, referred to as the first positive polarization. We first focus on the response of the LaTiO3/SrTiO3 sample shown in Figure 3. In this sample, increasing the gate voltage causes the resistance of the 2-DEG, after decreasing slightly, to saturate quickly and become independent of gate voltage. This behaviour is unexpected because, according to electrostatic laws, more electrons are added to the 2-DEG and therefore the resistance should decrease. This first positive polarization is irreversible: when the gate voltage is decreased from its maximum at  , the reverse resistance curve deviates from the first forward curve. The carrier density n was extracted from a two-carrier analysis of the Hall effect at high magnetic field (45 T) as described in reference [14] and Supplementary material. It was found to be constant during the first positive polarization, a behaviour consistent with the saturation of the resistance. Similar to the resistance curve, when the gate voltage is decreased after being increased to
, the reverse resistance curve deviates from the first forward curve. The carrier density n was extracted from a two-carrier analysis of the Hall effect at high magnetic field (45 T) as described in reference [14] and Supplementary material. It was found to be constant during the first positive polarization, a behaviour consistent with the saturation of the resistance. Similar to the resistance curve, when the gate voltage is decreased after being increased to  , the reverse carrier density curve does not follow the first forward curve. These two behaviours are in agreement with the irreversible situation described in Figure 2d. After the heterostructure is initially cooled, its Fermi level lies very close to the top of the well. Increasing the gate voltage adds electrons at the interface that quickly fills the highest energy sub-bands at the top of the well. After a certain time, these electrons eventually escape into the conduction band of the SrTiO3 substrate, causing the saturation of the carrier density and the resistance of the 2-DEG. Note that this saturation is not associated with an increase of the gate current, suggesting that charges are trapped in the system.
, the reverse carrier density curve does not follow the first forward curve. These two behaviours are in agreement with the irreversible situation described in Figure 2d. After the heterostructure is initially cooled, its Fermi level lies very close to the top of the well. Increasing the gate voltage adds electrons at the interface that quickly fills the highest energy sub-bands at the top of the well. After a certain time, these electrons eventually escape into the conduction band of the SrTiO3 substrate, causing the saturation of the carrier density and the resistance of the 2-DEG. Note that this saturation is not associated with an increase of the gate current, suggesting that charges are trapped in the system.
Beyond our initial experiments, we studied the irreversibility of the first positive polarization in further detail. After cooling a LaTiO3/SrTiO3 heterostructure to 4.2 K, we measured its sheet resistance as a function of gate voltage by using different polarization procedures (Fig. 4a). Different from our previous measurements, in this experiment we applied a negative first polarization down to  . Doing so increased the resistivity – an expected behaviour, as electrons are removed from the 2-DEG – and we observed no saturation. As the voltage returns to VG = 0 V, the forward resistance curve appears to match the first reverse curve. However, when the gate voltage is further increased to the value
. Doing so increased the resistivity – an expected behaviour, as electrons are removed from the 2-DEG – and we observed no saturation. As the voltage returns to VG = 0 V, the forward resistance curve appears to match the first reverse curve. However, when the gate voltage is further increased to the value  and then decreased back to VG = −200 V, the reverse resistance curve deviates from the first forward curve. This new curve is fully reversible as long as the gate voltage is not increased above
and then decreased back to VG = −200 V, the reverse resistance curve deviates from the first forward curve. This new curve is fully reversible as long as the gate voltage is not increased above  . We replicated this pattern with increasing maximum gate voltages of VG (
. We replicated this pattern with increasing maximum gate voltages of VG ( and
and  ).
).
Resistance of the LaTiO3/SrTiO3 sample measured for several forward sweeps (ΔVG > 0) and reverse sweeps (ΔVG < 0) with a starting VG of 0 V (“start” point).
We first sweep the VG to −200 V and then increase it to a maximum value  before sweeping it back to −200 V. We repeated this operation with increasing gate voltage maximum of
before sweeping it back to −200 V. We repeated this operation with increasing gate voltage maximum of  and
and  . Red markers indicate the region in which we observed relaxation. (b) Normalized resistance over time measured as a function of time after a ΔVG = ±10 V step in points labelled “A”, “B” and “C” on the R(VG) curves of panel (a). (c) Normalised resistance over time after a ΔVG = +10 V step at points labelled “D” and “E” on the R(VG) curves in (a). The resistance relaxation is fitted to a logarithm with form α + β log(t) (solid black lines).
. Red markers indicate the region in which we observed relaxation. (b) Normalized resistance over time measured as a function of time after a ΔVG = ±10 V step in points labelled “A”, “B” and “C” on the R(VG) curves of panel (a). (c) Normalised resistance over time after a ΔVG = +10 V step at points labelled “D” and “E” on the R(VG) curves in (a). The resistance relaxation is fitted to a logarithm with form α + β log(t) (solid black lines).
These results show that the well can be emptied (ΔVG < 0) and filled (ΔVG > 0) reversibly as long as the gate voltage is not increased beyond a critical value corresponding to the maximum value  previously applied to the metallic gate, a situation in which the Fermi level reaches the top of the well. Beyond this maximum value, we expect electrons to escape irreversibly from the 2-DEG into the SrTiO3 substrate. We performed the same measurements on an LaAlO3/SrTiO3 sample and we observed similar results (Fig. 5a). For this sample, the irreversible regime is reached at a gate voltage of 50 V indicating that the Fermi level after the initial cooling was slightly below the top of the well. As a consequence, at lower temperatures, the superconducting transition temperature saturates beyond this gate value (Fig. 5b and inset). To suppress the undesirable hysteresis effects, a first positive polarisation can be used as a forming process of the quantum well prior to other measurements13,14,20. However, in any case, the heavy doping of the 2-DEG will always be limited because the Fermi level cannot exceed the top of the quantum well.
previously applied to the metallic gate, a situation in which the Fermi level reaches the top of the well. Beyond this maximum value, we expect electrons to escape irreversibly from the 2-DEG into the SrTiO3 substrate. We performed the same measurements on an LaAlO3/SrTiO3 sample and we observed similar results (Fig. 5a). For this sample, the irreversible regime is reached at a gate voltage of 50 V indicating that the Fermi level after the initial cooling was slightly below the top of the well. As a consequence, at lower temperatures, the superconducting transition temperature saturates beyond this gate value (Fig. 5b and inset). To suppress the undesirable hysteresis effects, a first positive polarisation can be used as a forming process of the quantum well prior to other measurements13,14,20. However, in any case, the heavy doping of the 2-DEG will always be limited because the Fermi level cannot exceed the top of the quantum well.
(a) Sheet resistance of the LaAlO3/SrTiO3 sample during the first positive polarization at 4.2 K. Inset: Normalised resistance over time after a ΔVG = ±10 V step for points labelled “A”, “B” and “C” on the R(VG) curves in the main panel. The relaxation of the resistance is fitted to a logarithm with the form α + β log(t). (b) Sheet resistance of the LaAlO3/SrTiO3 sample as a function of temperature for different VG values during the first positive polarization, showing the saturation of Tc. Inset: Hysteresis of Tc as a function of VG for the first positive polarization.
Time-dependent measurement
We performed time-dependent resistivity measurements to assess how the 2-DEG responds to gate voltage steps of ΔVG = ±10 V. The expected corresponding modification of the carrier density is Δn = CaΔVG/e where Ca is the capacitance per unit of area of the SrTiO3 substrate. Representative results of these measurements are shown in Figure 4b and 4c for different filling situations, labelled “A”, “B”, “C”, “D” and “E” in Figure 4a. In the reversible regime, the resistance shows clears ΔR jumps before reaching a stable value (Fig. 4b). As expected, ΔR is positive when electrons are removed (ΔVG = −10 V, labels “A” and “B”) and negative when electrons are added (ΔVG = +10 V, label “C”). In contrast, after applying a voltage step of ΔVG = +10 V in the irreversible regime, the initial negative jump is followed by a slow increase of the resistance (Fig. 4c, labels “D” and “E”). We interpret this behaviour as the sign that electrons added to the 2-DEG by the gate-voltage step, eventually escaped from the well. By a first approximation, the resistance relaxation follows a logarithmic time dependence with the form α + β log(t). This relaxation must not be confused with the charging time of the capacitor RGCaA (A is the area of the sample) which is always present at a much shorter time scale (see Supplementary Information).
Model and Discussion
To analyze the relaxation in the irreversible regime we propose a model that describes the dynamics of electrons escaping from the well. We consider a 2D quantum well at the interface with an infinite barrier on the LaXO3(X = Al, Ti) side and a barrier of finite height EB on the SrTiO3 side (Inset of Fig. 6). A number nL of 2D parabolic sub-bands with energy Ei (i = 1,…,nL) and density of states  are filled. We assume that at a temperature T, electrons at the Fermi level EF can jump over the barrier with first order kinetics:
are filled. We assume that at a temperature T, electrons at the Fermi level EF can jump over the barrier with first order kinetics:

where n is the carrier density of the 2-DEG and k is the kinetic factor. This latter follows an Arrhenius law:  where the activation energy is Δ = EB − EF and ν is a characteristic frequency factor. In two dimensions, the electron density is given by
where the activation energy is Δ = EB − EF and ν is a characteristic frequency factor. In two dimensions, the electron density is given by

where NF = nLN is the total density of states at the Fermi energy and  . This situation is formally equivalent to the one with a single band of energy EL and a density of state NF. For a small variation of n, the temporal evolution of the Fermi energy is
. This situation is formally equivalent to the one with a single band of energy EL and a density of state NF. For a small variation of n, the temporal evolution of the Fermi energy is

At low temperature (kBT ≪ EF − EL), a good approximate solution to equation (3) is

where  is the Fermi level at t = 0+ (immediately after the voltage step, neglecting the short charging time RGCaA) and tE is the characteristic escape time given by
is the Fermi level at t = 0+ (immediately after the voltage step, neglecting the short charging time RGCaA) and tE is the characteristic escape time given by

where  is the carrier density at t = 0+. Therefore, the Fermi level is constant for t < tE, after which it decreases logarithmically. From (2) and (4) we can obtain the temporal dynamics of the 2-DEG Drude resistivity as
is the carrier density at t = 0+. Therefore, the Fermi level is constant for t < tE, after which it decreases logarithmically. From (2) and (4) we can obtain the temporal dynamics of the 2-DEG Drude resistivity as

where  is the resistivity at t = 0+. In Figure 6 we show the resistance relaxation after a ΔVG = +10 V step; this relaxation agrees very well with equation (6) over more than six decades of time (10 ms to 14 hours). A direct consequence of the logarithmic relaxation is the absence of an asymptotic value. However, on a linear scale the resistance changes very slowly after a few minutes, which can give a false impression of saturation. We emphasise here that the peculiar form of relaxation given by Eq. 6 is specific to the case of a well that empties itself and cannot describe other thermally activated mechanisms.
is the resistivity at t = 0+. In Figure 6 we show the resistance relaxation after a ΔVG = +10 V step; this relaxation agrees very well with equation (6) over more than six decades of time (10 ms to 14 hours). A direct consequence of the logarithmic relaxation is the absence of an asymptotic value. However, on a linear scale the resistance changes very slowly after a few minutes, which can give a false impression of saturation. We emphasise here that the peculiar form of relaxation given by Eq. 6 is specific to the case of a well that empties itself and cannot describe other thermally activated mechanisms.
Resistance over time of the LaTiO3/SrTiO3 sample after a ΔVG = +10 V step at t = 0, fitted by equation (6).
The escape time tE is 0.8 ± 0.1 s. Inset: Schematic of the situation considered to model the thermal escape of the electrons from the well.
To validate this model, we systematically studied how the relaxation depends on the polarization parameters. In particular, we measured the resistance relaxation after a ΔVG = +10 V step at different VG values (Fig. 7a) and for different steps of ΔVG = 5, 10, 20 and 40 V (Fig. 7c). The experimental data from both experiments agree with the theoretical equation (6), confirming that the model describes the phenomena we observed very well. We also observed the same agreement between experimental data and theoretical expectations for the LaAlO3/SrTiO3 sample (Supplementary Material). To understand how the escape time depends on VG and ΔVG, we can express equation (5) as

where γ and κ are constants whose expressions can be found in the Supplementary Material. Because the dielectric constant of SrTiO3 is electric-field-dependent, the capacitance Ca changes with gate voltage29. Therefore, the number of charges added by a constant voltage step ΔVG depends on the absolute value of the gate voltage. Figure 7b shows the linear variation of ln tE as a function of Ca as expected from equation (7). We also found ln tE to vary linearly with ΔVG for small gate voltage step ΔVG (figure 7d). For larger steps, the electrons are injected very high in the well complicating our determination of the short tE values.
(a) Resistance over time of the LaTiO3/SrTiO3 sample, measured at 4.2 K for different gate voltages after a ΔVG = +10 V step, fitted by equation (6). Arrows indicate tE values extracted from the fits. (b) Logarithm of tE, plotted as a function of Ca and fitted with equation (7) (red line). (c) Resistance over time, measured at 4.2 K for different steps ΔVG and fitted with equation (6). Arrows indicate tE values extracted from the fits. (d) Logarithm of tE plotted as a function of ΔVG and fitted with equation (7).
In the limit  , equation (6) reduces to R(t) = α + β log t where
, equation (6) reduces to R(t) = α + β log t where  . Figure 8a and 8b show that the β parameter increases linearly with temperature, as expected for a thermally activated mechanism. As already mentioned, electrons escaping into the SrTiO3 substrate get trapped by the defects of the crystal and no longer contribute to electronic transport. They can be released into the 2-DEG if the temperature of the sample increases above two characteristic values T1 ≈ 70 K and T2 ≈ 170 K for our LaTiO3/SrTiO3 sample (Fig. 8b). The trapping energy inferred from the temperature T1 is approximately 6 meV. As the electrons are trapped at a typical distance t from the interface comparable to the quantum well extension (~10 nm) which is much smaller than the thickness d = 500 μm of the SrTiO3 substrate, it is not possible to de-trapp the electrons with a negative gate voltage of reasonable value. Indeed, the potential energy transferred the electrons eVG × t/d always remains negligible compare to the trapping one. For this reason we do not observe hysteresis for negative gate voltages.
. Figure 8a and 8b show that the β parameter increases linearly with temperature, as expected for a thermally activated mechanism. As already mentioned, electrons escaping into the SrTiO3 substrate get trapped by the defects of the crystal and no longer contribute to electronic transport. They can be released into the 2-DEG if the temperature of the sample increases above two characteristic values T1 ≈ 70 K and T2 ≈ 170 K for our LaTiO3/SrTiO3 sample (Fig. 8b). The trapping energy inferred from the temperature T1 is approximately 6 meV. As the electrons are trapped at a typical distance t from the interface comparable to the quantum well extension (~10 nm) which is much smaller than the thickness d = 500 μm of the SrTiO3 substrate, it is not possible to de-trapp the electrons with a negative gate voltage of reasonable value. Indeed, the potential energy transferred the electrons eVG × t/d always remains negligible compare to the trapping one. For this reason we do not observe hysteresis for negative gate voltages.
(a) Parameter β of the logarithmic fit of the relaxation curves, as a function of gate voltage for three different temperatures and different values of ΔVG. (b) Parameter β (symbols) as a function of temperature for three selected gate voltages. The dashed lines correspond to a linear fit. (c) Resistance as a function of temperature measured for different sweep procedures: cooling down (triangle) and warming up (square) at VG = 0 (square), warming up with VG = 0 after a sweep to VG = −200 V (cross) and warming up with VG = 0 after a sweep to VG = +200 V (circle).
The same de-trapping behaviour has also been reported in LaAlO3/SrTiO330 at similar temperatures. The authors associated this behaviour to a thermally activated mechanism supported by exponential relaxations of conductivity near 70 K and 160 K. However, this behaviour should not be confused with the low-temperature logarithmic relaxations observed after a gate voltage step that we described in the present article. The relaxations at 70 K and 160 K are caused by thermal escape of electrons from traps with well-defined energy barriers, giving single exponential relaxations. In contrast, the low-temperature relaxations during the first positive polarisation are caused by electrons escaping from the quantum well with a time-dependent energy barrier, leading to logarithmic time dependence after a characteristic escape time. Similarly, relaxations associated to photoconductivity32,33 or relaxations sometimes observed at high temperature in SrTiO3 based structures and attributed to anions or vacancy diffusion12,31 also differ from the behaviour discussed in the present article.
In this article, we have taken into account only light electron bands to illustrate the quantum well. Note that the escape mechanism described here is inherent to the presence of a quantum well at the LaXO3(X = Al, Ti) SrTiO3 interface, disregarding the details of the band structure. It will remain valid even in the presence of a heavy band that has been theoretically predicted22,25,27 and seen by ARPES measurements to a certain extent38, since all the sub-bands cross the Fermi level (see Supplementary Figure S4). The escape mechanism does not depend on the exact shape of the potential well, which can be slightly modified by the presence of non-mobile charges at the interfaces (trapped electrons, impurities…) and can vary from sample to sample. It also does not depend strongly on the absolute carrier density of the as-grown sample since the location of the Fermi energy close to the top of quantum well at zero gate voltage is a simple consequence of the Poisson's equation.
In summary, we have shown that in LaAlO3/SrTiO3 and LaTiO3/SrTiO3 heterostructures, the Fermi level is instrinsically close to the top of the quantum well after the cool-down. When the carrier density is increased by an electrostatic back-gate voltage beyond a critical value, electrons escape into the SrTiO3 substrate at a rate well explained by a thermally activated leakage from the well. This phenomenon which appears both in LaAlO3/SrTiO3 and LaTiO3/SrTiO3 heterostructures, is directly responsible for the saturation of the 2-DEG properties with gate voltage, including the mobility and the carrier density, as well as the superconducting transition temperature observed at lower temperature. The exact capacity of the well– and, thus, the maximum carrier density– is mainly determined by growth conditions and can vary from sample to sample. While it is possible to deplete reversibly the quantum well by electrostatic back-gating, the filling is limited by the intrinsic location of the Fermi energy. To overcome this problem we suggest using double gated structures: A back gate could be used to engineer the shape of the quantum well which determines the carrier mobility through the bending of the SrTiO3 conduction band. In conjunction, a top gate can be used to add electrons to the well34,35.
Methods
Growth of the heterostructures
LaTiO3/SrTiO3 hetero-structures were grown at ITT Kanpur (India) using excimer laser based PLD system on commercially available (Crystal GmbH Germany) single crystal substrates of SrTiO3 (100) oriented. The substrates were treated with buffered HF to expose TiO2 terminated surface. Before deposition, the substrates were heated to 850–950°C for one hour in an oxygen pressure of 200 mTorr to realize surface reconstruction. The source of LaTiO3 was a stoichiometric sintered target of 22 mm in diameter which was ablated in an oxygen partial pressure of 1 × 10−4 Torr with energy fluence of 1 J/cm2 per pulse at a repetition rate of 3 Hz to achieve a growth rate of 0.12 Å/s. Under these conditions, the LaTiO3 phase is grown on SrTiO3 substrates, as shown by X-Rays diffraction patterns4. In this study, we used 15 u.c. thick LaTiO3 layers on 0.5 mm thick SrTiO3 substrates.
LaAlO3/SrTiO3 heterostructures were fabricated at UMR CNRS/Thales (Paris, France). A thin LaAlO3 film was deposited by PLD (Surface PLD system) on a TiO2-terminated (001)-oriented SrTiO3 substrate (Crystec and SurfaceNet). A buffered HF treatment followed by annealing, as described in Ref. [36], was used to obtain the TiO2 termination required to obtain the conducting electronic system at the interface. The KrF excimer (248 nm) laser ablates the single-crystalline LaAlO3 target at 1 Hz, with a fluence between 0.6 and 1.2 J/cm2 in an O2 pressure of 2 × 10−4 mbar. The substrate was typically kept at 730C° during the growth, monitored in real-time by RHEED. As the growth occurs layer-by-layer, it allows us to control the thickness at the unit cell level. After the growth of the film, the sample is cooled down to 500°C in 10−1 mbar of O2, where the oxygen pressure is increased up to 400 mbar. To reduce the presence of oxygen vacancies (in both the substrate and the film), the sample stays in these conditions for 30 minutes before being cooled down to room temperature37. The substrate-target distance was about 57 mm, leading to a growth rate of about 0.2 Å/s in the above conditions. In this study, we used 5 u.c. thick LaAlO3 layers on 0.5 mm thick SrTiO3 substrates.
References
Ohtomo, A. & Hwang, H. Y. A high-mobility electron gas at the LaAlO3/SrTiO3 heterointerface. Nature 427, 423–426 (2004).
Reyren, N. et al. Superconducting interfaces between insulating oxides. Science 317, 1196–1199 (2007).
Perna, P. et al. Conducting interfaces between band insulating oxides: The LaGaO3/SrTiO3 heterostructure. Appl. Phys. Lett. 97, 152111 (2010).
Biscaras, J. et al. Two-dimensional superconductivity at a Mott insulator/band insulator interface LaTiO3/SrTiO3 . Nature Commun. 1, 89 (2010).
Brinkman, A. et al. Magnetic effects at the interface between non-magnetic oxides. Nature Mater. 6, 493–496 (2007).
Ben Shalom et al. Anisotropic magnetotransport at the SrTiO3/LaAlO3 interface. Phys. Rev. B 80, 140403 (2009).
Li, L., Richter, C., Mannhart, J. & Ashoori, R. C. Coexistence of magnetic order and two-dimensional superconductivity at LaAlO3/SrTiO3 interfaces. Nature Phys. 7, 762–766 (2011).
Bert, J. A. et al. Direct imaging of the coexistence of ferromagnetism and superconductivity at the LaAlO3/SrTiO3 interface. Nature Phys. 7, 767–771 (2011).
Reyren, N. et al. Anisotropy of the superconducting transport properties of the LaAlO3/SrTiO3 interface. Appl. Phys. Lett. 94, 112506 (2009).
Copie, O. et al. Towards Two-Dimensional Metallic Behavior at LaAlO3/SrTiO3 Interfaces. Phys. Rev. Lett. 102, 216804 (2009).
Basletic, M. et al. Mapping the spatial distribution of charge carriers in LaAlO3/SrTiO3 heterostructures. Nature Mat. 7, 621–625 (2008).
Thiel, S., Hammerl, G., Schmehl, A., Schneider, C. W. & Mannhart, J. Electron Gases in Oxide Heterostructures. Science 313, 1942–1945 (2006).
Caviglia, A. D. et al. Electric field control of the LaAlO3/SrTiO3 interface ground state. Nature 456, 624 (2008).
Biscaras, J. et al. Two-dimensional superconductivity induced by high-mobility carrier doping in LaTiO3/SrTiO3 heterostructures. Phys. Rev. Lett. 108, 247004 (2012).
Biscaras, J. et al. Multiple Quantum Criticality in a two-dimensional superconductor. Nature Mat. 12, 542–548 (2013).
Bibes, M. Villegas, J. E. & Barthlmy, A. Ultrathin oxide films and interfaces for electronics and spintronics. Adv. Phys. 60, 5–84 (2011).
Takagi, H. & Hwang, H. Y. An Emergent Change of Phase for Electronics. Science 327, 1601–1602 (2010).
Mannhart, J. & Schlom, D. G. Oxide Interfaces - An Opportunity for Electronics. Science 327, 1607–1611 (2010).
Hwang, H. Y. et al. Emergent phenomena at oxide interfaces. Nature Mat. 11, 103–113 (2012).
Bell, C. et al. Dominant Mobility Modulation by the Electric Field Effect at the LaAlO3/SrTiO3 Interface. Phys. Rev. Lett. 103, 226802 (2009).
Caviglia, A. D. et al. Tunable Rashba Spin-Orbit Interaction at Oxide Interfaces. Phys. Rev. Lett. 104, 126803 (2010).
Popovic, Z., Satpathy, S. & Martin, R. M. Origin of the Two-Dimensional Electron Gas Carrier Density at the LaAlO3 on SrTiO3 Interface. Phys. Rev. Lett. 101, 256801 (2008).
Kancharla, S. S. & Dagotto, E. Metallic interface at the boundary between band and Mott insulators. Phys. Rev. B 74, 195427 (2006).
Salluzzo, M. et al. Orbital Reconstruction and the Two-Dimensional Electron Gas at the LaAlO3/SrTiO3 Interface. Phys. Rev. Lett. 102, 166804 (2009).
Son, W.-J., Cho, E., Lee, B., Lee, J. & Han, S. Density and spatial distribution of charge carriers in the intrinsic n-type LaAlO3/SrTiO3 interface. Phys. Rev. B 79, 245411 (2009).
Delugas, P. et al. Spontaneous 2-Dimensional Carrier Confinement at the n-Type SrTiO3/LaAlO3 Interface. Phys. Rev. Lett. 106, 166807 (2011).
Park, S. Y. & Millis, A. J. Charge density distribution and optical response of the LaAlO3/SrTiO3 interface. Phys. Rev. B 87, 205145 (2013).
Meevasana, W. et al. Creation and control of a two-dimensional electron liquid at the bare SrTiO3 surface. Nature Mater. 10, 114–118 (2011).
Neville, R. C., Hoeneisen, B. & Mead, C. A. Permittivity of Strontium Titanate. J. Appl. Phys. 43, 2124 (1972).
Seri, S., Schultz, M. & Klein, L. Thermally activated recovery of electrical conductivity in LaAlO3/SrTiO3 . Phys. Rev. B 87, 125110 (2013).
Shultz, M. & Klein, L. Relaxation of transport properties in electron-doped SrTiO3 . Appl. Phys. Lett. 91, 151104 (2007).
Rastogi, A., Pulikkotil, J. J., Auluck, S., Hossain, Z. & Budhani, R. C. Photoconducting state and its perturbation by electrostatic fields in oxide-based two-dimensional electron gas. Phys. Rev. B 86, 075127 (2012).
Di Gennaro, E. et al. Persistent Photoconductivity in 2D Electron Gases at Different Oxide Interfaces. Adv. Optical Mater. 1, 834–843 (2013).
Forg, B., Richter, C. & Mannhart, J. Field-effect devices utilizing LaAlO3 – SrTiO3 interfaces. Appl. Phys. Lett. 100, 053506 (2012).
Hosoda, M., Hikita, Y., Hwang, H. Y. & Bell, C. Transistor operation and mobility enhancement in top-gated LaAlO3/SrTiO3 heterostructures. Appl. Phys. Lett. 103, 103507 (2013).
Koster, G., Kropman, B. L., Rijnders, G. J. H. M., Blank, D. H. A. & Rogalla, H. Quasi-ideal strontium titanate crystal surfaces through formation of strontium hydroxide. Appl. Phys. Lett. 73, 2920 (1998).
Cancellieri, C. et al. Influence of the growth conditions on the LaAlO3/SrTiO3 interface electronic properties. Europhys. Lett. 91, 17004 (2010).
Berner, G. et al. Direct k-Space Mapping of the Electronic Structure in an Oxide-Oxide Interface. Phys. Rev. Lett. 110, 247601 (2013).
Acknowledgements
The authors gratefully thank M. Grilli and S. Caprara for stimulating discussions. High-magnetic field measurements were performed at the LNCMI Toulouse with the help of D. LeBoeuf and C. Proust. This work was supported by the french ANR and the Région Ile-de-France through CNano IdF and Sesame programs, as well as partially supported by Euromagnet II. The work at IIT Kanpur was funded by Council of Scientific and Industrial Research. R.C.Budhani acknowledges the J.C. Bose Fellowship from the Department of Science and Technology, Government of India.
Author information
Authors and Affiliations
Contributions
A.R. and R.C.B. prepared the LaTiO3/SrTiO3 samples. N.R. and E.L. prepared the LaAlO3/SrTiO3 samples. J.B. and S.H. performed the measurements, assisted by C.F.-P., J.B., J.L. and N.B. carried out the analysis of the results and wrote the article.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Electronic supplementary material
Supplementary Information
Supplementary information
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article's Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder in order to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Biscaras, J., Hurand, S., Feuillet-Palma, C. et al. Limit of the electrostatic doping in two-dimensional electron gases of LaXO3(X = Al, Ti)/SrTiO3. Sci Rep 4, 6788 (2014). https://doi.org/10.1038/srep06788
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep06788
This article is cited by
-
Coexistence and coupling of ferroelectricity and magnetism in an oxide two-dimensional electron gas
Nature Physics (2023)
-
Direct visualization of electronic transport in a quantum anomalous Hall insulator
Nature Materials (2023)
-
Designing spin and orbital sources of Berry curvature at oxide interfaces
Nature Materials (2023)
-
Superfluid stiffness of a KTaO3-based two-dimensional electron gas
Nature Communications (2022)
-
Hysteretic temperature dependence of resistance controlled by gate voltage in LaAlO3/SrTiO3 heterointerface electron system
Scientific Reports (2022)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.