Introduction

Accurate, remote temperature probing is a critical component of many emerging medical and biomedical technologies1,2,3. The lack of suitable technological options to assess the temperature of a targeted site has limited the large-scale marketing of hyperthermia treatment4,5,6,7, gene therapy8,9,10 and thermally controlled drug delivery protocols11,12,13. Breakthroughs in basic research are also expected if a noninvasive, accurate, sensitive and robust thermometer is made available for probing cellular compartments14,15,16. Thus, it is of significant interest to develop noninvasive, accurate approaches for the measurement of temperature, including the integration of a biocompatible sensor with a robust protocol for acquiring and handling thermometric properties.

To date, in vivo temperature probing techniques that are suitable for biological nanoscaled environments and have greater accuracy are not yet available. Optical17,18,19,20,21 and magnetic22,23,24 nanothermometers for noninvasive temperature measurements have been recently proposed. However, the drawback of optical approaches is the limited ability of light to penetrate deep into tissues, whereas magnetic approaches provide less accurate temperature measurements, thus limiting the development of hyperthermia techniques for both clinical use and basic research. Magnetic nanothermometry for in vivo applications does not pose the same drawbacks as optical approaches with respect to the difficulty in stimulating and detecting the signal from magnetic-labelled deep tissues for processing. Additionally, magnetic nanothermometry could potentially probe a single nanoparticle within cellular organelles using microSQUID25, whereas optical approaches may trigger apoptosis under intense illumination26,27.

In this study, the highest accuracy (0.017°C) achieved for noninvasive magnetic nanothermometry near the physiological temperature is reported. Our approach is based on the measurement of magnetisation as the thermometric property. The key aspects of temperature probing using magnetic nanoparticles (MNPs), such as the model construction, inverse calculation method, saturation magnetisation and applied magnetic field, are reported. A commercial sample (see the Methods section) was used to assess the temperature accuracy to confirm our findings based on simulations (see Simulation in Supplementary). The agreement between the calculated temperature and the temperature provided by SQUID is excellent.

Results

Fundamental theory

The magnetisation and susceptibility of MNPs are temperature-dependent properties and when properly recorded and manipulated, they provide a platform for nanothermometry in in vivo assays28,29. The magnetisation (M) of MNPs at a given temperature (T) under applied magnetic fields (H) follows the Langevin function (see Equation (1) in the Methods section). The simulation of M × H can be performed using Equation (1) because it varies significantly and monotonically with T, thus revealing the suitability of the magnetisation curve for nanothermometry applications (see Fig. 1). The temperature can be obtained by collecting the M × H datasheet and, subsequently, by applying the Langevin function and performing an inverse calculation (see the model construction and inverse calculation in Methods and Supplementary Information). However, the challenge of achieving a high degree of temperature precision is related to the approach used to establish the experimental conditions and that used to manipulate the recorded M × H datasheet. The work presented here bridges this gap.

Figure 1
figure 1

The simulated normalized magnetisation of MNPs at different temperatures.

Full size image

Magnetisation versus H/T curves

The model construction for temperature probing, as presented herein, shows that deviations between experimental and theoretical data (M × H) significantly affect the temperature probing capability. The variation of the M × H/T curve with temperature reveals that the magnetisation (M) decreases as the temperature (T) increases, as shown in Figure 2. The first concern is the temperature dependence of the saturation magnetisation (Μs). The data presented in Figure 2 clearly indicate the impact of the MsV × T behaviour (V is the MNP volume); the M × H/T curves are slightly and systematically downshifted as the temperature increases, even for temperature variations as small as 10 K (see the inset in Fig. 2). A significant change in temperature error is expected while neglecting the MsV × T behaviour, which can be described by Bloch's law23,30. According to the constructed model an omitted temperature variation in the M × H/T curve, such as the minimum shift of about 0.0002 emu with a relative shift of 0.255% between the black and the red curves (check the inset of Fig. 2), may cause a temperature error of about 0.79 K (0.255% × 310 K = 0.79 K). Therefore, the Bloch's law was used to achieve the optimal y* solution for the temperature calculation (see Equation (4) in Methods). Given the model construction, three combinations of theoretical models and inverse calculation methods (see Model Construction and Inverse Calculation in Supplementary) were employed (model-method) to process the experimental magnetisation data. Figure 3 shows the ΜsV × T data (employing Bloch's law) while using the three model-method combinations under different values of the maximum applied magnetic field (Hmax).

Figure 2
figure 2

The temperature over the field dependence of the magnetisation recorded from the magnetic nanoparticle-based powder sample obtained from the magnetic fluid (sample SOR-10) using the SQUID system.

The inset shows a magnification of the M × H/T curves in the H/T range of 2.25 to 2.55 Oe/K.

Full size image
Figure 3
figure 3

The average magnetic moment calculated using different combinations of models and inverse calculation methods for different maximum values for the applied magnetic field.

TM, TL and LL represent the calculated saturation magnetisation using a combination of Taylor's expansion and the inverse calculation based on the matrix, Taylor's expansion and the inverse calculation based on the least square error and Langevin's function and the inverse calculation based on the least square error, respectively. The solid line indicates the best fit using Bloch's Law (see Equation (4) in the Methods section). (a), (b), (c) and (d) represent different calculations with respect to a maximum applied magnetic field of 200, 400, 600 and 800 Oe.

Full size image

Magnetic moment and Bloch's law

The calculation of ΜsV × T can be significantly affected by the selection of Hmax, as well as by the model-method employed. For Hmax = 200 Oe, the ΜsV × T calculation using a combination of Taylor's expansion and the inverse calculation method based on the least square error (TL), or a combination of Langevin's function and the inverse calculation method based on the least square error (LL), are similar (see Fig. 3a). Furthermore, the obtained ΜsV × T can be sufficiently fitted by Bloch's law (solid line in Fig. 3a). This result indicates that Hmax = 200 Oe fulfils the condition of the lower magnetic fields for Taylor's expansion, thus indicating that the expansion can describe the magnetisation curve without producing a truncation error. However, the ΜsV × T curve calculated using the combination of Taylor's expansion and the inverse calculation based on the matrix solution (TM) is significantly affected by noise (see Fig. 3a) and is not accounted for by Bloch's law (see the discussion of Figs. S2 and S3 in Supplementary). At Hmax = 400 Oe, the ΜsV × T curve calculated using the model-method TL presents a slight deviation from the model-method LL, yet was still able to be fitted by Bloch's law (see Fig. 3b). Therefore, Hmax = 400 Oe results in a Taylor's expansion that generates a truncation error, although not a fatal truncation error, while describing the ΜsV × T curve; therefore, the result is in good agreement with the simulation (see the discussion of Figs. S4 and S5 in Supplementary). When Hmax increases beyond 400 Oe, the calculated ΜsV × T curve cannot be fitted by Bloch's law due to a fatal truncation error that occurs when using the Taylor's expansion to describe the magnetisation curve. However, the fitting of the calculated ΜsV × T curves using the model-method TM improves as Hmax increases (see Fig. 3c and 3d). For temperature probing and the temperature accuracy evaluation, we consider only the ΜsV × T data properly fitted using Bloch's law.

Temperature probing

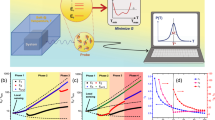
Figure 4 shows the experimental results of the temperature errors using three model-method combinations, as well as Equation (4) (see Methods). Setting Hmax = 200 Oe, the temperature error using the model-method TL (ET_TL) and the model-method LL (ET_LL) are similar. Both approaches provide a maximum error of 0.74 K with a standard deviation of 0.46 K (see Fig. 4a). This finding indicates that at lower magnetic fields, the Taylor's expansion properly describes the magnetisation data without introducing truncation error (see Fig. S4 in Supplementary). At Hmax = 400 Oe, the Taylor's expansion leads to truncation error (see Fig. 3b). However, the truncation error corresponding to the temperature error is not fatal and can be eliminated by calibrating ΜsV. More specifically, temperature probing using the model-method TL provides a maximum error of 0.282 K with a standard deviation of 0.171 K. These numbers are close to the values yielded by the model-method LL (0.277 K maximum error and 0.169 K standard deviation), as shown in Figure 4b. As Hmax increases to 600 and 800 Oe, a fatal truncation error causes a poor fitting of the ΜsV × T data by Bloch's law, thus eliminating the possibility of temperature probing with greater accuracy. Compared with Taylor's expansion, the model construction based on Langevin's function effectively eliminates the impact of the truncation error using the Μs calibration and temperature probing. Moreover, compared with the inverse calculation method based on the matrix solution, the inverse calculation method based on the least square error permits increased rejection of the impact of noise on the accuracy of the temperature measurement (see Fig. S4 in Supplementary). At different Hmax values, the temperature probing results are better with the combination of Langevin's function and the least square error than with the matrix solution. At Hmax = 800 Oe, the maximum error of the temperature using the model-method LL is approximately 0.022 K with a standard deviation of 0.017 K, whereas with the matrix solution, the maximum temperature error is 0.25 K with a standard deviation of 0.15 K.

Figure 4
figure 4

The temperature probing errors using three combinations of models and inverse calculation methods at different maximum applied magnetic fields of (a) 200, (b) 400, (c) 600 and (d) 800 Oe with the same point number of 20.

TT represents the theoretical value and ET_TM, ET_TL and ET_LL represent the temperature probing errors using a combination of Taylor's expansion and the inverse calculation based on the matrix, Taylor's expansion and the inverse calculation based on the least-square error and Langevin's function and the inverse calculation based on the least square error, respectively.

Full size image

Applied magnetic field

The protocol developed for temperature probing using MNPs, as well as the corresponding accuracy, requires a discrete measurement of the magnetisation curve. Figure 5 shows the experimental results of temperature probing using MNPs at different values of Hmax (200 to 800 Oe). Only the optimal combination of the model-method LL was used to assess the performance of the temperature probing approach. Figure 5a shows the probed temperature and Figure 5b presents the corresponding temperature errors. The temperature accuracy varies significantly as Hmax changes from 200 to 800 Oe (see Fig. 5). Using Hmax = 200 Oe, the maximum temperature error recorded is 0.74 K, whereas for Hmax = 800 Oe, the maximum temperature error is reduced to 0.022 K. Moreover, the error bar for repeated measurements decreases as Hmax increases from 200 to 800 Oe. The inset of Figure 5a shows the experimental and calculated magnetisation at 310 K (Hmax = 800 Oe), with a standard deviation less than 1.9 × 10−4 emu. Additionally, the standard deviation of the temperature error for the six measured temperature points varies significantly with Hmax (see Fig. 5b). As Hmax increases from 200 to 800 Oe, the standard deviation of the temperature error decreases from 0.45 to 0.017 K (see Fig. S6 in Supplementary). Our experiments show that temperature probing can be improved by a factor of 20 as Hmax is increased from 200 to 800 Oe.

Figure 5
figure 5

Temperature probing using magnetic nanoparticles in the temperature range from 310 to 320 K.

(a), The average estimated temperature (ET) from 3 repeated measurements and the inset show the experimental and calculated magnetisation curves at the temperature of 310 K. (b), The temperature probing error and the inset represent the standard deviation curve of the temperature probing error and the maximum magnetic field. ET1-ET4 represent the estimated temperatures (errors) for different values of the maximum applied magnetic field (200, 400, 600 and 800 Oe) for the same point number (20).

Full size image

In conclusion, this report theoretically and experimentally investigated the factors that impact temperature probing to achieve high accuracy using magnetic nanoparticles. Our report also presented a theoretical model construction, an inverse calculation method, the temperature dependence of the saturation magnetisation and the maximum value of the applied magnetic field. The results of our simulation and experimental work indicated the combination of the Langevin function and the inverse calculation based on the least square error as the best option for magnetic nanothermometry, yielding a temperature accuracy of 0.017 K (0.0055% relative accuracy). The proposed protocol provides the tool required for breakthroughs in biomedical applications and basic cell research.

Methods

Experimental description

The establishment of magnetic nanoparticles as a material platform for robust, noninvasive and accurate magnetic nanothermometers requires the successful handling and modelling of high-quality magnetic versus applied field (M × H) experimental data, recorded at different temperatures in the range of study. Within the material platform, a useful system is represented by magnetic fluids (MFs), which are composed of magnetic nanoparticles stably dispersed throughout a host liquid. The magnetic sample used in the present study to assess the temperature and the accuracy of the temperature measurement is a commercial magnetic fluid (sample SOR-10), purchased from Ocean Nanotechnology (Springdale, USA), that consists of maghemite nanoparticles with an average diameter of approximately 10 nm. The nanoparticles are surface-coated with oleic acid and dispersed in an organic solvent at a concentration of 5 mg-Fe/mL. The magnetic nanoparticle-based sample used to record the magnetisation data was obtained from drying the solvent out from the magnetic fluid sample (SOR-10). The discrete magnetisation curves (M × H) were recorded at different temperatures using a MPMS3 SQUID system from Quantum Design (San Diego, CA, USA) within the selected range of −Hmax to Hmax and with the same discrete point number of 40. For each magnetisation curve, the corresponding temperature provided by SQUID is calculated based on 40 repeated measurements.

Model and calculation

The first-order Langevin function describing the superparamagnetism of nanosized particles is specified by23,24:

where x = ϕMs and y = MsV/kT. The particle volume fraction within the magnetic particle-based sample is described by ϕ. Μs is the particle's saturation magnetisation; V is the particle's volume; H is the applied magnetic field; and T is the absolute temperature. In the approach for temperature probing using magnetic nanoparticles (MNPs), Equation (1) plays a key role. Recently, temperature probing using Equation (1) to describe the magnetic susceptibility of MNPs was theoretically and experimentally studied by employing Taylor's expansion of Equation (1) and an inverse calculation method based on the matrix solution24. The Langevin function describing the particle's magnetisation was expanded in a Taylor's series at lower magnetic fields24:

In Equations (1) and (2), x and y are variables. Recording discrete magnetisation curves (Mi × Hi data set) allows the construction of a set of equations to assess the temperature (T). Here, we present the matrix solution and the least square error to perform the calculation for the constructed set of equations. However, the set of equations based on Equation (1) only allows an inverse calculation based on the least square error, whereas the set of equations based on Equation (2) allows for an inverse calculation based on both the matrix solution and the least square error. Moreover, the set of equations based on Equation (1) or (2), as well as the employed calculation methods, affect the accuracy of the optimal solution (x*, y*).

Temperature dependence of the saturation magnetisation

To assess the temperature with high accuracy, the temperature dependence of the nanoparticle's saturation magnetisation (Ms) should be considered and is approximated by23,30:

where Mso represents the saturation magnetisation at 0 K and a is a positive constant in units of K−3/2. With the optimisation, the optimal solution y* is rewritten as:

Finally, the temperature probing is determined by solving Equation (4).