Introduction

The hybrid coherent coupling1 between electromagnetic and mechanical degrees of freedom is at the heart of cavity optomechanics2,3,4. In general, optomechanical couplings can be classified into two categories: linear or quadratic couplings. Namely, the coupling term is proportional to either x or x2 (x being the mechanical displacement). For a mechanical resonator, a linear coupling corresponds to a force acting upon the mechanical resonator and this leads to a displacement of its equilibrium position. However, for a quadratic coupling, it will change the resonant frequency of the mechanical resonator (in the new representation, rather than in the original representation). This is because the quadratic-coupling term can be integrated into the potential energy of the harmonic oscillator (changing the effective stiffness of a spring) and hence the frequency of the mechanical resonator is renormalized. This renormalized harmonic oscillator is related to the original one by a squeezing transformation.

To better understand and exploit optomechanical couplings, it is highly desirable to realize these couplings in the single-photon strong-coupling regime, in which the couplings involving a single photon can produce observable effects on both mechanical and electromagnetic signals. Such a regime is important to test the fundamentals of quantum theory5,6,7,8 and to explore possible applications of optomechanical devices to future quantum technology9,10,11. In the past several years, much attention has been paid to the single-photon strong-coupling regime of linear coupling12,13,14,15,16,17,18,19,20,21,22,23,24,25. Considerable theoretical studies, such as photon statistics16,17,21,22,23 and mechanical-state engineering24, have been carried out in this regime. Two theoretical proposals26,27 have recently been suggested to reach this regime using superconducting circuits with Josephson junctions. In addition, experimental advances in linear optomechanics are being made towards the single-photon strong-coupling regime12,13,14,15. However, for the quadratic coupling, though much attention has been paid to this area28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48, not much work has been devoted to the single-photon strong-coupling regime because the currently attainable coupling strength is weak. Recently, some methods have been proposed to increase the quadratic optomechanical coupling strength or to seek other possible realization of quadratic optomechanics. For example, an experiment42 demonstrated that the quadratic coupling strength can be increased significantly using a fiber cavity with a smaller mode size and a smaller and lighter membrane. A measurement-based method has also been proposed to obtain an effective quadratic optomechanics36. In addition, some other systems, such as trapped cold atoms or a dielectric nano- or microparticle, have been suggested to simulate an effective quadratic optomechanical coupling44. These works provide a possibility of studying the quantum nonlinearity in quadratic optomechanics. Motivated by these advances, it is of interest to study the quadratic optomechanical coupling in the single-photon strong-coupling regime.

When a quadratic optomechanical cavity works in the single-photon strong-coupling regime, the frequency change of the mechanical resonator induced by a single photon will, in turn, significantly affect the cavity field, causing some observable features in the cavity photon spectrum. Thus, a natural question arises: how the spectrum may characterize the single-photon strong-coupling regime? In this paper, we answer this question by calculating analytically the spectrum of single-photon emission and scattering. In particular, we build a connection between the spectral features and the system's inherent parameters. We also clarify the condition for observing the phonon sidebands in the spectra. It should be pointed out that below we assume that the mechanical resonator has been pre-cooled to a low-phonon-number regime. Moreover, in typical optomechanical systems, the optical decay rate γc is much larger than the mechanical decay rate γM. Under these two conditions, we will only consider the optical dissipation and neglect the mechanical dissipation. This is because the emission and scattering processes will be completed in a time interval . During this period the mechanical dissipation is negligible. In this issue, the emission and pulse-scattering cases are different from the continuous-wave driving case. When the system is driven by a continuous-wave field, the mechanical dissipation should be included for the steady-state solution46.

Accompanying the processes of single-photon absorbtion and emission, the total system experiences transitions involving phonon sidebands and hence the frequency of the emitted photon will be related to the states of the phonon sidebands due to energy conservation. This relation leads to the generation of photon-phonon entanglement. Since the emitted photon exists in the continuous modes of the outside fields, this entangled state involves a single mode of phonons and a set of continuous modes of a single photon. In general, it is hard to characterize such type of entanglement. However, from the point of view of a single photon rather than photon modes, we could treat this entanglement as a bipartite one between a single photon and the phonon mode. For a pure initial state, the linear entropy can be employed to describe this entanglement.

Results

Quadratic optomechanical system

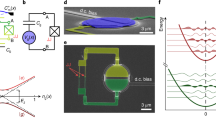
We consider a quadratic optomechanical system with a “membrane-in-the-middle” configuration [see Fig. 1(a)], where a thin dielectric membrane is placed inside a Fabry-Pérot cavity. We model the moving membrane as a harmonic oscillator and focus on a single-mode field in the cavity. When the membrane is placed at a node (or antinode) of the intracavity standing wave, the cavity field will quadratically couple to the mechanical motion of the membrane. Let us denote the position and momentum operators of the membrane as x and p, then the Hamiltonian of the system is (with )

where a† and a are the creation and annihilation operators of the single-mode cavity field, respectively. In the quadratic coupling case, the cavity-field frequency depends on the mechanical motion by ωc(x) = ωc + ηx2, with , where ωc is the cavity-field frequency when the membrane is at rest. The parameters M and Ω in Eq. (1) are the mass and frequency of the mechanical mode. By reorganizing the coupling term between the zero-point energy of the optical mode and the mechanical motion into the mechanical potential energy, we have

where is the renormalized frequency of the membrane. We note that it is justified to work in the representation of the mechanical frequency ωM, because the coupling term ηx2/2 always exists. By introducing the mechanical creation and annihilation operators b† and b, by and , the Hamiltonian, up to a constant term (ωc + ωM)/2, becomes28

where g0 = η/(2MωM). The third term in Eq. (3) describes a quadratic optomechanical coupling with a strength g0 between the cavity field and the membrane. We point out that since the reorganized frequency ωM of the mechanical mode also depends on the coupling strength g0 by , the ratio of the coupling strength g0 over the mechanical frequency ωM is bounded by g0/ωM < 1/2. However, below we also consider parameters by extending the scope of the ratio beyond this bound. This is because the bound can be exceeded in some other quadratical optomechanical systems, such as trapped cold atoms.

Figure 1
figure 1

Quadratic-optomechanical system and the energy-level structure.

(a) Schematic diagram of a quadratic optomechanical system with a “membrane-in-the-middle” configuration. (b) The diagram of the energy-level structure (unscaled) of the optomechanical system when the cavity is in a vacuum or contains a single photon.

Full size image

When there are s photons in the cavity, the last two terms in Hamiltonian (3) can be renormalized as a harmonic-oscillator Hamiltonian with the resonant frequency . To keep the stability of the membrane (i.e., the frequency should be a positive number), the strength g0 should satisfy the condition (ωM + 4sg0) > 0. The photon number operator a†a in Hamiltonian Hopc is a conserved quantity and hence for a given photon number s, the coupling actually takes a quadratic form sg0(b† + b)2, which can be diagonalized with the single-mode squeezing transformation. Denoting the harmonic-oscillator number states of the cavity field and the membrane as |s〉a and |m〉b (s, m = 0, 1, 2, …) respectively, then the eigensystem of the Hamiltonian Hopc can be obtained as

where we introduce the s-photon coupled membrane's resonant frequency and energy-level shift δ(s),

The s-photon squeezed phonon number state in Eq. (4) is defined by

where is a squeezing operator with the squeezing factor

We note that the eigensystem of the Hamiltonian (3) has been derived in previous studies31,45,46. In the zero-photon case, we have , and δ(0) = 0. For following convenience, the energy-level structure of the system in the zero- and one-photon cases is shown in Fig. 1(b).

To include the dissipation of the cavity field, we assume that the cavity photons can couple with the outside fields through the coupling mirror. Without loss of generality, we model the environment of the cavity field as a harmonic-oscillator bath. Then the Hamiltonian of the whole system including the optomechanical cavity and the environment can be written as

where the annihilation operator ck describes the kth mode of the outside fields with resonant frequency ωk. The coupling between the cavity field and the outside fields is described by the photon-hopping interaction with strength ξ. Since the decay rate γM of the mechanical resonator is much smaller than the decay rate γc of the cavity, then during the emission and wave-packet scattering time interval , the damping of the membrane is negligible. In this work we take into account the dissipation of the cavity and neglect the mechanical dissipation.

States in the single-photon subspace

In the rotating frame with respect to , the Hamiltonian (8) becomes

where Δk = ωk − ωc is the detuning of the kth mode photon from the cavity frequency. The total photon number, , in the whole system is a conserved quantity because of [N, HI] = 0. Denoting for conciseness, a general state in the single-photon subspace of the total system can be written as

where denotes the state with the cavity in the single-photon state |1〉a, the membrane in the single-photon squeezed number state (hereafter we call it as squeezed number state for conciseness) and the outside fields in a vacuum . Also |0〉a|m〉b|1k〉 denotes the state with a vacuum cavity field |0〉a, the membrane in the number state |m〉b and one photon in the kth mode of the outside fields |1k〉. The variables Am(t) and Bm,k(t) are probability amplitudes.

We point out that these squeezed number states in Eq. (10) satisfy the completeness (Ib is the identity operator in the Hilbert space of mode b) and orthogonality . Moreover, the overlap between the squeezed number state and the harmonic-oscillator number state |m〉b is determined by the relation

where η(1) = (1/4) ln(1 + 4g0/ωM) and the function Floor[x] gives the greatest integer less than or equal to x. In principle, the state of the whole system can be obtained by solving the Schrödinger equation under a given initial condition. Below we will consider single-photon emission and scattering.

Single-photon emission

In the single-photon emission case, a single photon is initially inside the cavity and the outside fields are in a vacuum. Without loss of generality, we assume that the initial state of the membrane is an arbitrary number state |n0〉b. Once the solution in this case is obtained, the solution for the general initial membrane state can be obtained accordingly by superposition. In this case, with the Laplace transform method, we obtain the long-time solution for these probability amplitudes as and

where we introduce the cavity-field decay rate γc = 2πξ2 and add the subscript n0 in and to mark the membrane's initial state |n0〉b.

In the long-time limit, the single photon completely leaks out of the cavity and hence the cavity is in a vacuum . The amplitude exhibits a clear physical picture for the single-photon emission. Specifically, the initial state |1〉a|n0〉b can be expanded as , with . For each component , the single-photon emission process induces the transition . The corresponding transition amplitude is proportional to the numerator in Eq. (12). Due to the quadratic terms of b and b† in Sb(η(1)), |m〉b and should have the same parity, i.e., being odd or even. Consequently, the phonon number distribution in the long-time state of the membrane will have the same parity as its initial component |n0〉b. In addition, we can derive the resonant condition in this emission process from the energy-level structure in Fig. 1(b). For the transition , the frequency of the emitted photon is , which is consistent with the resonance condition

obtained from the pole of the denominator in Eq. (12).

We know from Eqs. (10) and (12) that, corresponding to the initial state , the long-time state of the whole system is

Therefore, when the membrane is initially in a general density matrix

the long-time state of the whole system can be obtained by superposition as

Here the density matrix elements are .

To characterize the quadratic optomechanical coupling, a useful quantity is the single-photon emission spectrum, i.e., the probability distribution of the emitted photon. For the initial membrane state (15), the emission spectrum is defined by

In Fig. 2, we plot the emission spectrum S(Δk) versus the photon frequency Δk, for various values of g0 and γc, when the membrane is initially in its ground state |0〉b. We see from Eq. (12) that both and ωM > γc might be the resolved-sideband condition. For a positive g, then ωM > γc could make sure that the two conditions are met, because of . We found that, in the case of , the phonon-sideband evidence is negligible. So, in this paper, we consider ωM > γc as the resolved-sideband condition. Figures 2(a–c) are plotted in the resolved-sideband regime ωM > γc so that the phonon sideband peaks could be used to characterize the coupling strength g0. When g0 < γc [Fig. 2(a)], the spectrum is approximately a Lorentzian function with width γc and center Δk = δ(1). In this case, there are no sideband peaks in the spectrum. However, the sideband peaks become visible when g0 > γc. Physically, when the displacement of the membrane equals its zero-point fluctuation, the photon frequency shift induced by the quadratic optomechanical coupling is g0. To resolve this frequency shift from the Lorentzian spectrum of a free cavity, the condition g0 > γc should be satisfied. Such a condition can also be understood by examining the height of these peaks in the spectrum. To resolve a peak in the spectrum, the peak height should be much higher than the tail of its neighboring Lorentzian. This requires in the resolved-sideband regime. As an example, we analyze the special case of . In the resolved-sideband regime and under the initial state |0〉b, we expand S(Δk) up to second-order in g0/ωM. Then, the height of the sideband peak located at Δk = δ(1) − 2ωM can be obtained as . Since the main peak of the spectrum is approximately a Lorentzian function , then the requirement

leads to the condition .

Figure 2
figure 2

Single-photon emission spectrum S(Δk) versus Δk for various values of g0 and γc.

Panels (a–c) are plotted in the resolved-sideband regime (γc/ωM = 0.2), while (d) is plotted in the unresolved-sideband regime (γc/ωM = 1.5). The membrane's initial state is |0〉b.

Full size image

We remark that the positions of these sideband peaks in Fig. 2 are determined by the resonance condition (13) and these sideband peaks are not periodic because of the difference between and ωM. Also, for the initial state |0〉b of the membrane, the contributing m and n in Eq. (13) should be even numbers due to the parity requirement. In Figs. 2(a–c), the peak located at Δk = δ(1) is the main peak (corresponding to the transition ). Hence, we can resolve the main peak from the Lorentzian spectrum for a free cavity when δ(1) > γc, which requires g0 > γc(1 + γc/ωM). The peak located at Δk = δ(1) − 2ωM corresponds to the transition . Moreover, the peak located at corresponds to the transition . Finally, Fig. 2(d) is plotted in the unresolved-sideband regime. We can see from Fig. 2(d) that, even though the system works in the single-photon strong-coupling regime, there are no sideband peaks in the spectrum. This fact indicates that the resolved-sideband regime and the single-photon strong-coupling condition are two combined necessary requirements for observing sideband peaks in the emission spectrum.

To illustrate how the spectrum depends on the initial state of the membrane, we plot in Fig. 3 the spectrum S(Δk) versus Δk when the membrane is initially in either the Fock states |0〉b and |1〉b, the coherent state |β = 1〉b, or the thermal state . For the initial state |0〉b, the main peak (with the location Δk = δ(1)) in Fig. 3(a) is related to the transition . The two peaks located at Δk = δ(1) − 2ωM and correspond to the transitions and , respectively. For the initial state |1〉b, the main peak (located at ) in Fig. 3(b) is related to the transition . The other two peaks located at and correspond to the transitions and , respectively. Here, Figs. 3(a) and (b) only show even- and odd-parity sideband peaks, respectively. However, the coherent and thermal states contain both odd- and even-parity number states and hence we can see both odd- and even-parity sideband peaks in Figs. 3(c,d). The positions of these sideband peaks are consistent with those in Figs. 3(a,b).

Figure 3
figure 3

Single-photon emission spectrum S(Δk) versus Δk for various initial states of the membrane.

The membrane is initially prepared in either the Fock states |0〉b and |1〉b, the coherent state |β = 1〉b, or the thermal state . Other parameters are γc/ωM = 0.2 and g0/wM = 0.6.

Full size image

In the long-time limit, though the single photon is completely leaked out of the cavity, its state is still entangled with the mechanical mode. This entanglement involves a single mode of phonons (the mechanical degree of freedom) and a set of modes of the photon because the single photon is distributed into the continuous fields outside the cavity. In general, it is difficult to clearly describe the structure of this entanglement. However, from the viewpoint of a single photon, we can characterize the entanglement as a bipartite one between a single photon and a single mode of phonons. In particular, we will consider a pure initial-state case so that the long-time state of the total system is also pure; then we can employ the linear entropy to quantity this bipartite entanglement.

When the membrane is initially in the general state (15), the long-time state of the total system is given by Eq. (16). In terms of Eq. (12), the reduced density matrix of the membrane can be obtained as

where

The linear entropy49 of the density matrix (19) is

In Fig. 4, we plot El versus g0 for initial Fock states |n0〉b of the membrane, i.e., . Figure 4 shows that (as a general trend) El increases with increasing g0. However, there are some resonance dips in the linear entropy when g0 takes some special values. The locations of these dips can be determined from the poles of the denominator in Eq. (20), i.e., , here the values of (l − l′) and (s′ − s) should be even numbers because of the parity requirement in the transitions. For example, there is a dip at g0/ωM = 0.75, which corresponds to |(l − l′)/(s′ − s)| = 2. In addition, corresponding to the membrane's initial states |0〉b, |1〉b and |2〉b, the linear entropy keeps increasing. We may roughly explain this phenomenon by analyzing the magnitude distribution of these factors and . When n0 changes from 0 to 2, the magnitude distribution of these transitions elements (for different s′) becomes increasingly smoother. This implies that the number of contributing coefficients increases and hence the entanglement increases.

Figure 4
figure 4

The linear entropy El in the emission case.

The linear entropy El versus the optomechanical coupling strength g0, when the initial state of the membrane is |0〉b, |1〉b and |2〉b. Here γc/ωM = 0.2.

Full size image

Single-photon scattering

In the single-photon scattering case, the single photon is initially in a Lorentzian wave packet in the outside fields, where Δ0 and are the detuning center and spectral width of the photon. In this case, with the Laplace transform method, the long-time solution (i.e., , ) of these probability amplitudes is obtained as and

Here the subscript n0 in these amplitudes is used to mark the initial state of the membrane. In the long-time limit, the single photon will completely leak out of the cavity and hence we have . It can be seen from that there are two physical processes in the single-photon scattering. (i) The single-photon direct-reflection process: the incident photon is directly reflected by the mirror, without entering the cavity. This process is described by the first term of . (ii) The photon-membrane interacting process: the single photon enters the cavity to couple with the moving membrane and eventually leaks out of the cavity via the cavity decay channel. This process is described by the second term (i.e., the second and third line) in Eq. (22). In this process, the system experiences the transitions , These transitions are governed by the two resonance conditions

which can be derived from either the energy level structure in Fig. 1(b) or the poles of the probability amplitude (22). Interestingly, the second line in Eq. (22) is a Lorentzian wave packet with spectral width and center Δk = Δ0 + (n0 − m)ωM. In comparison to the initial Lorentzian wave packet, the shift of the wave packet center is equal to the energy variance of the membrane. Moreover, the third line in Eq. (22) has a similar form as Eq. (12) for the single-photon emission process.

The single-photon scattering spectrum can be calculated in terms of Eqs. (17) and (22). We see from Eq. (22) that either the second line or the third line could cause phonon sidebands and the conditions for resolving these sidebands due to the two lines are and ωM > γc, respectively. Here, γc is the system's inherent parameter while is an externally controllable parameter. In the following, we first consider the case of so that the observed sideband peaks are caused purely by the system inherent effect. In Fig. 5, we plot the spectrum S(Δk) versus the photon frequency Δk for various values of g0 and γc. When g0 < γc, there are no peaks in the spectrum [Fig. 5(a)]. The phonon sideband effect can be observed in the scattering spectrum when g0 > γc and ωM > γc [Figs. 5(b,c)]. Owing to the interference between the direct reflection process and the photon-membrane interacting process, there exist both peaks and dips in the spectrum. In Figs. 5(b,c), the dips represent the transition , while the peaks correspond to the transition . In addition, in the unresolved-sideband regime (γc > ωM), there are no peaks even in the single-photon strong-coupling regime [Fig. 5(d)].

Figure 5
figure 5

Single-photon scattering spectrum S(Δk) versus Δk for various values of g0 and γc.

Figures (a–c) are plotted in the resolved-sideband regime (γc/ωM = 0.2), while (d) is plotted in the unresolved-sideband regime (γc/ωM = 1.5). The membrane's initial state is |0〉b. Other parameter are Δ0 = δ(1) and .

Full size image

We now consider the near-monochromatic case (). In Fig. 6(a), we plot the scattering spectrum in the case of γc > ωM and . This figure exhibits phonon sideband peaks and hence indicates that also provides the condition for observing the phonon sideband peaks due to the second line in Eq. (22). We point out that this provides a way to characterize the coupling strength g0 from the scattering spectrum in the case of γc > ωM. Another benefit in the near-monochromatic case is that we can conveniently control the exciting transition by choosing the frequency of the incident photon. In Figs. 6(b,c), we choose the frequency of the incident photon as Δ0 = δ(1) and to resonantly excite the system from |0〉a|0〉b to and , respectively. In the emission process, the membrane will experience the transitions from and to |n〉b (n = 0, 2, 4, …). Therefore, the maximal frequency sideband peaks should be located at Δk = δ(1) and , respectively. In addition, the period of these peaks is 2ωM. Similar to the emission case, the scattering spectrum also depends on the initial state of the membrane. In Fig. 6(d), we plot the scattering spectrum when the membrane's initial state is coherent state |α = 1〉b. Though the initial coherent state contains both even- and odd-parity states, the spectrum only exhibits similar peaks as those in Fig. 6(b). This is because the incident photon (with Δ0 = δ(1)) only resonantly excites the membrane from |0〉b to ; other transitions from |n〉b to (n, n′ = 1, 2, 3, …, with the same parity) are significantly suppressed due to the large detuning. A further photon emission process induces the transitions from to |n〉b (n = 0, 2, 4, …).

Figure 6
figure 6

Single-photon scattering spectrum S(Δk) versus Δk for various Δ0 and initial states of the membrane.

The panel (a) is plotted in the unresolved-sideband regime (g0/ωM = 2 and γc/ωM = 1.5), while panels (b–d) are plotted in the resolved-sideband regime (g0/ωM = 0.8 and γc/ωM = 0.2). The frequency center Δ0 of the incident photon is and δ(1) in other panels. The membrane's initial state is the ground state |0〉b in panels (a–c) and the coherent state |a = 1〉b in (d). The parameter .

Full size image

Similar to the emission case, the scattered photon is completely emitted out of the cavity in the long-time limit; and the state of the photon is entangled with the mechanical membrane. For the membrane's initial state |n0〉b, the linear entropy of the long-time reduced density matrix of the membrane was calculated exactly. This is not shown here because the analytical solution is long. We can examine how the linear entropy depends on the system parameters: the incident photon frequency Δ0 and the optomechanical coupling strength g0. In the near-monochromatic limit , we plot, in Fig. 7(a), the linear entropy El as a function of Δ0 when the quadratic optomechanical coupling g0 takes various values. We can see from Fig. 7(a) that there are resonant peaks in the entropy. For a given g0, the locations of these peaks are Δ0 = δ(1) and , which are determined by the resonance conditions in the dominant transitions in the photon injection process: and .

Figure 7
figure 7

The linear entropy El in the scattering case.

(a) The linear entropy El versus Δ0 for various values of g0. The initial state of the membrane is |0〉b. (b) The linear entropy El versus g0 when the membrane is initially in states |0〉b, |1〉b and |2〉b. Here the frequencies of the incident photon are Δ0 = δ(1), and , respectively. Other parameters are γc/ωM = 0.2 and .

Full size image

We also investigate the dependence of the linear entropy El on the coupling strength g0 when the incident photon is in resonance with the transitions. In Fig. 7(b), we plot the entropy El versus g0 when the initial state of the membrane is |0〉b, |1〉b and |2〉b. Here the single photon is resonantly injected into the cavity. Corresponding to the initial states |0〉b, |1〉b and |2〉b, the driving frequencies are Δ0 = δ(1), and , respectively. These drivings determine the dominant photon-injection transitions: , and . We can see that, in the resonant scattering case, the linear entropy increases when increasing g0.

Discussion

Although the currently-available quadratic couplings are too weak to reach the single-photon strong-coupling regime, advances have recently been made in the enhancement of this coupling strength. In quadratic optomechanics, the coupling strength is , where xzpf is the zero-point fluctuation of the mechanical membrane and , with ωc(x) being the x-dependent cavity frequency. Recently, the value of η has been increased significantly from about 30 MHz/nm2 (in Ref. [33]) to 20 GHz/nm2 (in Ref. [42]) using a fiber cavity with a smaller mode size. For a xzpf ~ 41 fm, suggested in Ref. 28, the coupling strength is g0 ~ 2π × 5.35 Hz. If the cavity decay rate γc ~ MHz, the coupling strength needs to be further increased by five orders of magnitude to reach the single-photon strong-coupling regime. From , we can see that the g0 can be increased by obtaining a larger η or xzpf. This requires the improvement of experimental conditions. In addition, the model under investigation is a general quadratic optomechanical Hamiltonian36. It can also be realized in various physical systems such as ultracold atoms and superconducting circuits. In the linear optomechanical coupling case, the ultracold atom system has been demonstrated to approach the single-photon strong-coupling regime13,14 and the superconducting circuit system has been estimated to be in this regime26,27. Moreover, other methods have been recently explored to achieve effective strong quadratic optomechanics. For example, a measurement-based method has been proposed to perform this mission. Based on these achievements, it might be possible to pursue the single-photon strong-coupling regime in quadratic optomechanics.

In the above discussions, we did not include the mechanical dissipation. Now we give a rough estimate for the influence of the mechanical dissipation on our results. In our considerations, all the results are determined by the probability amplitudes given in Eqs. (12) and (22). To evaluate the influence of the mechanical dissipation, we introduce an imaginary decay factor into the resonant frequency of the mechanical mode, i.e., approximately replacing ωM with , where is the thermal phonon occupation. In this way we can estimate the effect of the thermal mechanical dissipation. If , then the mechanical dissipation is negligible. This is because, in the low-temperature regime, the imaginary part in the denominators of Eqs. (12) and (22) can still be approximated by γc/2 and the exponential factor is almost 1 during the time scale t ~ 1/γc.

We have analytically studied the single-photon emission and scattering in a quadratically-coupled optomechanical system. By treating the optomechanical cavity and its environment as a whole system, we have obtained the emission and scattering solutions using the Laplace transform method. Based on our solutions, we have calculated the single-photon emission and scattering spectra and found relations between the spectral features and the system's inherent parameters. In particular, we have clarified the condition under which phonon sideband peaks can be observed in the photon spectra. In the resolved-sideband regime ωM > γc, the phonon sidebands are visible when g0 > γc, while the condition for resolving the photon-state energy-level shift δ(1) is g0 > γc(1 + γc/ωM). We have also investigated the creation of photon-phonon entanglement in the emission and scattering processes. This entanglement was created due to the energy requirement in the photon absorption and emission processes and it was treated as a bipartite one from the viewpoint of a single photon rather than photon modes. We have considered the pure state case so that the linear entropy can be used to characterize this entanglement between the phonon mode and a single photon.

Finally, we want to mention several possible applications of the single-photon emission and scattering processes. (i) Since the emission and scattering spectra are related to the eigen-energy of the system, we can read out the system parameters, such as coupling strength and mechanical frequency, from the spectra. (ii) We can infer the initial state information of the mechanical resonator based on the single-photon spectra, similar to the linear optomechanics case50. As a special example, the initial temperature of the mechanical membrane can also be determined from the spectra. (iii) The entanglement generated in the emission and scattering processes involves phonons and one outgoing photon. So this entanglement could be used to implement quantum information processing tasks, where phonons and photons are used as information memory and carriers, respectively.

Methods

Solving the equations of motion for probability amplitudes

According to Eqs. (9), (10) and the Schrödinger equation , we obtain the equations of motion for the probability amplitudes

where the single-photon coupled membrane's frequency and energy-level shift are given by and . In addition, the coefficients and can be calculated using Eq. (11).

The equations of motion (24) for the probability amplitudes may be solved with the Laplace transform method under a given initial condition. In the single-photon emission case, a single photon is initially inside the cavity and the outside fields are in a vacuum. For the mechanical mode, we first assume that its initial state is an arbitrary number state |n0〉b. Based on the solution in this case, the solution for the general initial membrane state can be obtained accordingly by superposition. For the initial state , the corresponding initial condition for Eq. (24) is and Bm,k(0) = 0. In the single-photon scattering case, the single photon is initially in a Lorentzian wave packet in the outside fields and the cavity is in a vacuum |0〉a. We also assume that the membrane is initially in the number state |n0〉b and then the initial condition for Eq. (24) becomes Am(0) = 0 and , where Δ0 and are the detuning center and spectral width of the photon, respectively. Based on these initial conditions and the equations of motion, we may obtain the solution of these probability amplitudes using the Laplace transform method. The long-time solutions corresponding to the single-photon emission and scattering have been given in Eqs. (12) and (22), respectively.