Abstract
Multifractal, a special class of complex self-affine processes, are under recent intensive investigations because of their fundamental nature and potential applications in diverse physical systems. Here, we report on a novel light scattering-based inverse method for extraction/quantification of multifractality in the spatial distribution of refractive index of biological tissues. The method is based on Fourier domain pre-processing via the Born approximation, followed by the Multifractal Detrended Fluctuation Analysis. The approach is experimentally validated in synthetic multifractal scattering phantoms and tested on biopsy tissue slices. The derived multifractal properties appear sensitive in detecting cervical precancerous alterations through an increase of multifractality with pathology progression, demonstrating the potential of the developed methodology for novel precancer biomarker identification and tissue diagnostic tool. The novel ability to delineate the multifractal optical properties from light scattering signals may also prove useful for characterizing a wide variety of complex scattering media of non-biological origin.
Similar content being viewed by others
Introduction
Studies on structures and processes that exhibit self-similarity have evoked intensive investigations recently because of their fundamental nature and potential applications in diverse areas ranging from complex biological systems, material structures, electrical circuits to various optical phenomena1,2,3. Fractal measures are characterized by regular (exact fractals) or random (statistical fractals) hierarchical scaling down to arbitrarily small scales1,2,3. While most of the aforementioned self-similar processes typically exhibit monofractal behaviour that can be adequately described by a single scaling exponent, a few special class of complex processes are associated with more complicated scaling behaviour which may be thought of as consisting of many interwoven fractal subsets, each of them characterized by their own local scaling exponent4. Such complex self-affine processes are also ubiquitous in nature and are extensively studied for diverse applications, for example in physiological time series of heartbeat5,6, turbulence7,8,9, Sun's magnetic field dynamics10, stock market fluctuations11 and so forth.
Elastically scattered light contains information about the spatial frequency spectrum of the investigated object, providing a useful route to probe the self-similarity in the spatial distribution of its refractive index (RI). Indeed, such light scattering measurements have been explored for characterizing the fractal structures of biological tissues12,13. Elastic scattering of light in tissue originates from the micro/nano-scale spatial fluctuations of RI at the cellular, sub-cellular and extra-cellular levels14. Accordingly, subtle changes in the tissue physical/optical properties leave its characteristic signatures, as manifest in the variation of scattered light intensity (either as a function of angle or wavelength). We have recently shown that the spatial distribution of tissue refractive index exhibits multifractality, indicative of its morphological and ultra-structural tissue content15. Extraction and quantification of these multifractal optical properties from light scattering signal may prove to be valuable for non-invasive detection of diseases, including early detection of cancer or even precancer. We thus address the outstanding challenge of the corresponding inverse problem; that is, given a tissue light scattering signal (either as a function of angle or wavelength), is it possible to extract its multifractal properties? In tissues, the wide range of spatial scaling of the inhomogeneities and the complicated nature of the spatial correlations present between them contributes in a complex intertwined way to the light scattering signal. The method we propose is based on Fourier domain pre-processing via the Born approximation, followed by the Multifractal Detrended Fluctuation Analysis. The approach is experimentally validated in synthetic multifractal scattering phantoms and tested on tissue slices (tissue sections of human cervix of different pathology grades). The light scattering-derived multifractal tissue optical properties yield valuable information on subtle changes in the index inhomogeneity distribution of tissue; they also appear sensitive in detecting cervical precancerous alterations through an increase of multifractality with pathology progression. The potential of the developed methodology for novel precancer biomarker identification as a tissue diagnostic tool is thus suggested.
Theory
Multifractal Detrended Fluctuation Analysis (MFDFA)
A statistically homogeneous fractal (monofractal) series is one whose variance exhibits a power law scaling described by a single global Hurst exponent, H (0 < H < 1)1,2,3. A multifractal signal, on the other hand, exhibits many interwoven fractal subsets characterized by different local Hurst exponents4,5. Multifractal Detrended Fluctuation Analysis (MFDFA) is a generalized approach to characterize such complex multi-affine processes4,16. Briefly, the fluctuation profile Y(i) (series of length N, i = 1…..N) is divided into Ns = int (N/s) non-overlapping segments m of equal length s. The local trend of the series (ym(i)) is determined by least square polynomial fitting of each segment m of the series. These are then subtracted from the segmented profile to yield the detrended fluctuations and the resulting variance is determined as16

The generalized moment (q) dependent fluctuation function is then constructed by averaging the variances over all the segments as

The scaling behavior is subsequently studied under the assumption of power law scaling Fq(s) ~ sh(q). Using this approach, any non-stationary multifractal signal can be characterized via two sets of scaling exponents: (i) the generalized Hurst exponent h(q) and (ii) the classical multifractal scaling exponent τ(q), along with the singularity spectrum f(α). These are related as16


Where α is the singularity strength and the full width of f(α); Δα (taken at f(α) = 0) is a quantitative measure of multifractality.
Light scattering based inverse analysis in Born approximation
The MFDFA approach can be directly employed on spatial variation of refractive index to quantify signature of multifractality from any random medium such as tissue15. Here, we describe an inverse analysis strategy for extraction and quantification of multifractality from the corresponding light scattering signal. Consider a weakly fluctuating scattering medium having normalized RI fluctuations  . Here, r is the location within the volume and n0 is the average RI of the medium; the fluctuating part of index Δn(r) gives rise to phase distortion and scattering. In the first order Born approximation (weak variations of Δn(r)), the elastic scattering field for scalar excitation can be related to Δn(r) via a Fourier transformation17,18. For continuous random media such as tissues, we further assume that the index variations arise from statistical inhomogeneities having different spatial dimensions, albeit with similar amplitude of fluctuating index δn (scatterers having different sizes but similar RI)18,19,20. With this approximation, the expression for scattered intensity is given by
. Here, r is the location within the volume and n0 is the average RI of the medium; the fluctuating part of index Δn(r) gives rise to phase distortion and scattering. In the first order Born approximation (weak variations of Δn(r)), the elastic scattering field for scalar excitation can be related to Δn(r) via a Fourier transformation17,18. For continuous random media such as tissues, we further assume that the index variations arise from statistical inhomogeneities having different spatial dimensions, albeit with similar amplitude of fluctuating index δn (scatterers having different sizes but similar RI)18,19,20. With this approximation, the expression for scattered intensity is given by

Here, k = 2π/λ, β is the scattering vector with modulus β = 2k sin(θ/2), θ is the scattering angle, λ is the wavelength (β is related to the spatial frequency ν via β = 2πν); σ = n0δn represents the index fluctuation strength and η(r) is the corresponding spatial distribution of index inhomogeneities. It is evident that any signature of multifractality hidden in η(r) would be encoded in I(β), in the Fourier domain. Consequently, for media exhibiting statistical self-similarity in index fluctuations, the information on multifractality can in principle be obtained from the scattering signal as

The parameter η/(ρ) can be interpreted as index inhomogeneity distribution with spatial scale ρ, representing the randomness of the mediumin statistical sense, ρ = |r − r/| is the distance between any two medium points. In what follows, we demonstrate that η/(ρ) contains the essential multifractal features of index fluctuations in complex systems such as tissues, which can be extracted by employing multifractal analysis. For this purpose, (i) we employ MFDFA directly on the spatial variation of tissue RI, obtained from differential interference contrast (DIC) images of human cervical pathology (forward analysis); and (ii) quantify the multifractal tissue optical properties by employing MFDFA on the Fourier pre-processed light scattering data η/(ρ) (inverse analysis).
Results and discussion
Evidence of multifractality in tissue refractive index fluctuations
The evidence of multifractality in spatial variation of tissue RI is presented in Figure 1, using the DIC image of the connective tissue regions of typical grade-1 dysplastic/precancerous human cervical tissue. The recorded DIC image (Figure 1a) was pixel-wise unfolded in one linear direction to obtain the representative one dimensional index fluctuation series. This 1D RI fluctuation series was then analyzed via the Fourier and MFDFA methods. The resulting power spectrum of Fourier transformation (P(ν), ν being the spatial frequency here in μm−1) is shown in Figure 1b (axes are shown in natural logarithm scale). Statistical self-similarity is manifested as a power-law scaling of the spatial frequency distribution (P(ν) ≈ ν−γ) (Fig. 1b). As seen, the power law coefficient (slope γ) is not uniform throughout the entire ν range (Fig. 1b), suggesting multifractality. As expected from the Born approximation (equation (5)), the light scattering [P(ν) = I(ν) × k−4,  , θ = 150°, λ = 400–760 nm shown here] signal also yields multiple values for the spectral exponent (Fig. 1c). A factor of ~2 differences in the slope scaling exponents between the two approaches is due to the former being obtained from 1D Fourier transform of the index fluctuation, while the latter emerges via a 3D Fourier analysis of the scattering potential.
, θ = 150°, λ = 400–760 nm shown here] signal also yields multiple values for the spectral exponent (Fig. 1c). A factor of ~2 differences in the slope scaling exponents between the two approaches is due to the former being obtained from 1D Fourier transform of the index fluctuation, while the latter emerges via a 3D Fourier analysis of the scattering potential.
Evidence of multifractality in the spatial variation of tissue RI.
(a) DIC image of typical Grade I precancerous human cervix (connective tissue slice). (b) Fourier power spectrum of the generated 1D RI fluctuation series (shown in natural logarithm scale). Fitting at two selected ν-ranges (lower (green) and higher (red), respectively) and overall fitting (black) yield different values for slope (manifestation of multifractality) (c) The light scattering signal [P(ν) = I(ν) × k−4] recorded from the same tissue also yields multiple spectral slope exponents (fitting at two selected ν ranges and overall fitting on the entire ν range are shown). (d), (e), (f): Results of the MFDFA forward analysis on the detrended (by least square polynomial fitting) spatial index fluctuations (from the DIC image). (d) The variation of the moment (q) dependent fluctuation function Fq(s) with length scale s (constructed using Eq. 2). The points represent the MFDFA-derived values of Fq(s) and the lines are power law fitting. Considerable variation in the slopes of log Fq(s) vs log s with varying q confirms multifractality. (e) The variation of the generalized Hurst exponent h(q) (derived from the slopes of log Fq(s) vs log s) and the classical scaling exponent τ(q) (derived using Eq. 3) (inset). The points represent the MFDFA-derived values and the lines are guide for the eye (for these and all subsequent figures displaying these parameters). (f) The resulting singularity spectrum f(α) (derived using Eq. 4). The points represent the derived values for f(α) and the line represents the fitted data (using 2nd order polynomial) for this and all subsequent figures displaying f(α). The value for the full width of the fitted singularity spectrum, Δα (taken at f(α) = 0) is noted in the figure.
The corresponding results of MFDFA forward analysis are shown in Fig. 1d, e and f. Considerable variations in the slopes of logFq(s) vs logs with varying moment q furnish supporting evidence of multifractality (Fig. 1d). Its strength is subsequently quantified via the moment-dependent generalized Hurst exponent h(q) (Fig. 1e, derived from the slopes of logFq(s) vs logs) and the width (Δα) of the singularity spectrum f(α) (Fig. 1f, derived using equation (4)). Significant variations in h(q) and considerable magnitude of Δα ( = 0.42) demonstrate strong multifractality in the spatial variations of tissue RI.
Inverse analysis of multifractality from light scattering signal
We now turn to the more challenging inverse problem of extracting the multifractal optical properties from the light scattering signal. We employ MFDFA on the Fourier pre-processed light scattering data η/(ρ)(equation (6)). While the Born approximation for modelling light scattering in tissues is widely used12,13,14,18,19,20,21,22, employing MFDFA on the Fourier pre-processed light scattering signal is novel and as such requires validation. Making use of the Fourier optics experimental arrangement (see Figure 2a and Methods), validation was performed on synthetic statistical mono/multifractal scattering (diffracting) objects whose self-similar properties were user controlled. The mono/multifractal objects were realized by modulating the grey levels of the pixels of a transmissive liquid crystal-based twisted nematic spatial light modulator (SLM) through fluctuation series synthesized either by fractional Brownian motion (monofractal) or binomial multifractal model2,16 (see Methods and Supplementary information). Figure 2 shows the grey level distributions in the SLM pixels for a multifractal object (Fig. 2b), theoretical Fourier power spectrum of the synthesized multifractal image (Fig. 2c), corresponding variation of the recorded intensity in the CCD (Fourier) plane (Fig. 2d) and the results of MFDFA analysis on the Fourier pre-processed theoretical power spectrum and experimental intensity data (Fig. 2e). Comparison of h(q) spectrum derived from the experimental data and from the theoretical one shows excellent agreement. The experimental value h(q = 2) = 0.70, that obtained from the theoretical data (h(q = 2) = 0.67) and the known input for the fluctuation series (h(q = 2) = 0.69), are in close agreement (note, h(q = 2) correspond to the Hurst exponent of an equivalent monofractal series2,16). Based on this and other continuing validation studies (see Supplementary information), the strategy of Fourier domain preprocessing and its subsequent analysis using MFDFA appears valid for inverse extraction of multifractality and may be relevant for tissue examinations.
Control validation experiments on synthetic statistical multifractal scattering object.
(a) Fourier optics experimental arrangement. MO: microscope objective; P: pinhole; L1: collimating lens; FT Lens: Fourier transforming lens (focal length f). (b) Multifractal object realized by modulating the pixels of a transmissive liquid crystal-based twisted nematic spatial light modulator (SLM) through binomial multifractal model (input h(q = 2) = 0.69). Color bar represents grey level values (0–255). (c) Theoretical Fourier power spectrum of the multifractal image. (d) The experimentally recorded intensity in the CCD (Fourier) plane, shown as spatial frequency  (color bars represent intensity value). Fourier domain pre-processing was performed on both sets of data (c) and (d), which were subsequently analyzed using MFDFA. (e) The MFDFA-derived generalized Hurst exponent h(q) for the theoretical (blue) and experimental (red) data. The inset shows corresponding singularity spectra f(α). The values for the width of f(α), (Δα), are also noted in the inset. Excellent agreement between the experimentally derived value h(q = 2) = 0.70, obtained from the theoretical data (h(q = 2) = 0.67) and the controlled input for the synthesized fluctuation series (h(q = 2) = 0.69), suggests self-consistency in inverse analysis of multifractality.
(color bars represent intensity value). Fourier domain pre-processing was performed on both sets of data (c) and (d), which were subsequently analyzed using MFDFA. (e) The MFDFA-derived generalized Hurst exponent h(q) for the theoretical (blue) and experimental (red) data. The inset shows corresponding singularity spectra f(α). The values for the width of f(α), (Δα), are also noted in the inset. Excellent agreement between the experimentally derived value h(q = 2) = 0.70, obtained from the theoretical data (h(q = 2) = 0.67) and the controlled input for the synthesized fluctuation series (h(q = 2) = 0.69), suggests self-consistency in inverse analysis of multifractality.
Multifractal tissue optical parameters as novel biomarkers for precancer detection
Figure 3 displays the results of the inverse analysis performed on the light scattering spectra recorded (using the spectral light scattering measurement system, see Methods and Supplementary information) from a grade-1 dysplastic cervical tissue (corresponding to Fig. 1). Strong multifractality is once again evident from the large variations in the slopes of logFq(s) vs logs (Fig. 3c). The derived h(q) spectrum and the singularity spectrum f(α) (Fig. 3d and 3e) exhibits features similar to those obtained via forward analysis (Fig. 1e and 1f). Moreover, the derived h-value [h(q = 2) = 0.58] is in good agreement with the forward analysis result [h(q = 2) = 0.53]. This suggests self-consistency in inverse analysis of multifractality from tissue light scattering spectra. Note that even though the parameter η/(ρ), extracted via Fourier pre-processing, represents the index variations in a statistical sense over the probed tissue volume, it contains contributions of sub-micron level spatial index fluctuations (as evident from Fig. 3b). The multi-resolution capability of MFDFA allows one to further extract separately the contributing small scale (primarily via the negative moments q) and the large scale (via the positive moments q) fluctuations and quantify their statistical self-similar properties via h(q) (and τ(q)) and f(α)16. The observed considerable variations of h(q) (τ(q)) for negative q -values (Fig. 3d) and the resulting width of f(α) (Fig. 3e) underscores the importance of the small scale index fluctuations (possibly originating from the micro-architecture of the fibrous network of connective tissue). It may be pertinent to discuss here about the statistical nature of the variation of the MFDFA-derived singularity spectrum f(α). Note that f(α) contains relatively fewer data points for smaller values of α. This non-ideal nature of f(α) (as opposed to that expected for ideal multifractal fluctuation series) arises due to the strong contribution of the background Brownian type random fluctuations in the Fourier pre-processed light scattering data η/(ρ). Such background random fluctuations in turn originates from the associated randomness in the spatial index variation (as evident from Figure 1b, where the power spectrum of spatial index variation exhibit large background fluctuations in addition to the overall power law scaling behavior). Never-the-less, these results suggest that Fourier pre-processing of light scattering in Born approximation and its subsequent analysis through MFDFA captures and quantifies small spectral variations as signature of subtle (otherwise hidden) changes in the RI spatial distribution via the multifractal optical parameters. The possible interplay of the wavelength dependent tissue absorption on the light scattering inverse analysis method also worth a brief mention. Although, the biopsy tissue slices used in our study did not exhibit any significant spectral absorption features, in general, the light scattering spectra recorded from bulk tissues are expected to carry signature of absorption (primary candidates for absorptions in tissue in the visible wavelength region are the various forms of haemoglobins). Note that the signature of absorption typically manifests as sharp, localized (in the characteristic absorption bands) and distinct spectral features. Such regular trends in the spectral variation are expected to be removed via our pre-processing scheme of the light scattering spectral data (Fourier domain pre-processing employing Eq. 6 and subsequent detrending of the resulting fluctuations employing Eq. 1). Specifically, the de-trending process removes any regular trends (such as the ones resulting from distinct absorption spectral features) present in the Fourier pre-processed light scattering data η/(ρ). Moreover, one may also additionally employ methods such as polarization gating to reduce the signature of tissue absorption on light scattering spectra13,18.
Results of the inverse analysis performed on the light scattering spectra recorded from a grade-1 precancer human cervical tissue slice (corresponding to Fig. 1).
(a) The recorded light scattering intensity [I(ν) vs ν,  , θ = 150°, λ = 360–740 nm, shown here]. (b) The representative index fluctuations with spatial scale ρ (η/(ρ)) extracted via Fourier domain pre-processing (using Eq. 6) on I(ν) (shown following polynomial detrending). (c), (d), (e): Results of the MFDFA inverse analysis on the detrended fluctuations η/(ρ). (c) The variation of logFq(s) vs logs for different moments q( = −4 to +4 shown here). Multifractality in η/(ρ) is evident from significant variations in the slopes with varying q. (d) The MFDFA-derived moment dependence of generalized Hurst exponent h(q) and classical scaling exponent τ(q) (inset). (e) The resulting singularity spectrum f(α). Close agreement in the behavior of h(q) and values for h(q = 2) derived from this inverse analysis and that from the forward analysis of multifractality (Fig. 1d, e, f) suggests self-consistency.
, θ = 150°, λ = 360–740 nm, shown here]. (b) The representative index fluctuations with spatial scale ρ (η/(ρ)) extracted via Fourier domain pre-processing (using Eq. 6) on I(ν) (shown following polynomial detrending). (c), (d), (e): Results of the MFDFA inverse analysis on the detrended fluctuations η/(ρ). (c) The variation of logFq(s) vs logs for different moments q( = −4 to +4 shown here). Multifractality in η/(ρ) is evident from significant variations in the slopes with varying q. (d) The MFDFA-derived moment dependence of generalized Hurst exponent h(q) and classical scaling exponent τ(q) (inset). (e) The resulting singularity spectrum f(α). Close agreement in the behavior of h(q) and values for h(q = 2) derived from this inverse analysis and that from the forward analysis of multifractality (Fig. 1d, e, f) suggests self-consistency.
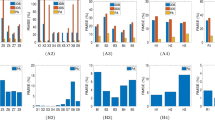
The newly derived multifractal tissue optical properties were investigated for discriminating different grades of cervical precancer. Twenty two precancerous and four normal connective tissue sections are analyzed in Figure 4. The observed trends are: (i) the values for h(q = 2) or τ(q = 2) are higher in normal tissues and decrease with increasing grades of precancer (e.g, h(q = 2) = 0.77 ± 0.01, 0.56 ± 0.01 and 0.42 ± 0.01 for normal, Grade I and Grade III tissues respectively); (ii) the magnitudes of Δα are larger for higher grades of precancer (e.g. Δα = 0.84 ± 0.03, 1.36 ± 0.10 and 1.67 ± 0.02 for normal, Grade I and Grade III tissues respectively). Note that the limiting values for h(q = 2) of unity and zero correspond to smooth Euclidean random field/marginal fractal (implying long range correlations) and a space-filling field/extreme fractal (anti correlated behavior) respectively. Reduction in the value for h(q = 2) with increasing pathology thus likely indicates increasing tissue roughness, or effectively the predominance of index inhomogeneities having smaller dimensions. Connective tissue is comprised of collagen fiber network with complex organization of constituent micro-fibrils; statistical self-affinity of fibrous network may manifest as the observed multifractality in spatial variation of RI. Reduced h(q = 2) may originate from volume fraction reduction of the fibrous network and/or fibers shortening/disorganization (both processes occurring with disease progression)23,24,25,26. Increased multifractality (larger value of Δα) at higher grades of precancer, on the other hand, may be a manifestation of the increased heterogeneity and the different scaling behavior of the small scale (possibly the constituent micro-fibril architecture in individual fibers) and the large scale (fibrous network) index fluctuations. This suggestion was initially tested in extracted Bovine collagen samples treated with 5% acetic acid (results not shown); this is known to degrade organized collagen fibrous structures by breaking cross-links23,24. Δα increased from ~1.4 to 1.8 after 30 minutes of acetic acid treatment. Note that we concentrate on connective tissue morphology (as opposed to the widely explored epithelial cell compartment) since progression of cancer involves altered interactions between epithelial cells and underlying connective tissue (stroma) and changes in stromal biology/morphology may precede and stimulate neoplastic progression in preinvasive disease25,26. The observed differences in the multifractal tissue scattering properties between normal and Grade I precancerous tissues thus points towards the ability of the method to quantify subtle morphological alterations in connective tissue as early signature of precancers.
Discrimination of different grades of precancers based on the light scattering-derived multifractal tissue optical properties.
Results from twenty two precancerous (Grade I - 12, Grade II -4 and Grade III -6) and four normal tissue sections are summarized. The multifractal parameters, Hurst exponent h(q = 2), classical scaling exponent τ(q = 2) and width of singularity spectrum Δα form the three axes. Higher grades of precancers are associated with increased anti-correlations of index fluctuations (increased roughness - reduction in h(q = 2) and τ(q = 2)) and stronger multifractality (increase in the value for Δα). These results provide some support those normal and precancerous tissues with different pathology grades can be discriminated using these derived multifractal parameters.
In conclusion, a novel light scattering-based inverse method is developed, validated and explored for extraction and quantification of multifractality in the spatial RI fluctuations of biological tissues. Experimental validation of this inverse analysis method in synthetic multifractal scattering phantoms and the agreement between the forward analysis on differential interference contrast image of tissue and inverse analysis from light scattering spectra, establishes self-consistency. The latter demonstrates that subtle changes in multifractal nature of tissue RI fluctuations can indeed be probed and quantified from light scattering spectra, despite numerous complexities associated with the wide range of spatial scaling of the index inhomogeneities, complex spatial correlations and the resulting intertwined nature of their contribution to the tissue light scattering signal. The demonstrated ability to delineate multifractal properties may provide a valuable noninvasive tool for characterization of tissue and wide variety of other complex scattering media of non-biological origin. Observed differences in the multifractal tissue optical properties between different grades of precancers show considerable promise as potential biomarkers for early detection. The ability to probe and quantify subtle morphological and structural alterations associated with precancer using the elastic backscattering spectra bodes well for in-vivo deployment, because the backscattering geometry is clinically convenient and the measurement technique is fairly straight-forward. Exploiting the elastic backscattering spectra (singly or weakly scattered) recorded from superficial tissue depths, in-vivo applications of this approach can be realized with a suitably designed fiber optic probes and/or by other methods (e.g., polarization gating) to eliminate multiply scattered light13. Finally, the multifractal inverse analysis of light scattering represents a fundamentally novel approach with much potential, but its actual benefits for in-vivo detection of precancers remain to be rigorously evaluated. We are currently initiating such investigations in our laboratory.
Methods
Histopathologically characterized (CIN or dysplasia grade I, II and III) biopsy samples of human cervical tissues with normal counterparts were obtained from G. S. V. M. Medical College and Hospital in Kanpur, India (Patient age 35–60 years; ntotal = 26, with ngrade I = 12, ngrade II = 4, ngrade III = 6; four biopsies from the normal counterparts, nnormal = 4). Standard histological preparation of the excised tissues involving fixation, dehydration, imbedding in wax, sectioning under a rotary microtome (thickness ~5 μm, lateral dimension ~4 mm × 6 mm) and subsequent de-waxing was employed. The control experiments were performed on the extracted Bovine collagen (Collagen from bovine achilles tendon, type I, C9879 SIGMA) samples. The collagen was treated with 5% (weight by volume) acetic acid and the light scattering spectra were recorded both before and after 30 minutes of treatment. Consent for the use of all the biopsy samples of human cervical tissues with normal counterparts in our study was obtained from the Ethical Committee, G. S. V. M. Medical College and Hospital, Kanpur, India. The methods were carried out in accordance with the approved guidelines.
A differential interference contrast (DIC) microscope (Olympus IX81, USA) was used to measure the spatial distribution of tissue refractive index (Figure 1a). Images were recorded with a CCD camera (ORCA-ERG, Hamamatsu, 1344 × 1024 pixels, pixel dimension 6.45 μm), at a magnification of 60×. The images were unfolded (pixel-wise) in one linear direction to obtain 1D fluctuation series and were subsequently forward analyzed for multifractality employing Fourier and MFDFA methods. The elastic scattering spectra from the tissue sections were recorded using angle resolved spectral light scattering measurements (see Supplementary information). Briefly, light from a Xe-lamp (HPX-2000, Ocean Optics, USA) was collimated using a combination of lenses and illuminated the tissue sample at the centre of a goniometric arrangement (spot size ~1-mm-diameter). The sample-scattered light was collimated with lenses and was focused into a collecting fiber probe coupled to a spectrometer (USB4000FL, Ocean Optics, USA) for wavelength resolved signal detection. The spectra were recorded (360–800 nm) with a spectral resolution of 2.05 nm, for the angular range θ = 10–150°, at 10° intervals. The spectra recorded at backscattering angle θ = 150° was used for the inverse multifractal analysis (Figure 1c, Figure 3).
For validation of inverse analysis (Fig. 2), we employed Fourier optics experimental arrangement (Fig. 2a). Briefly, the 632.8 nm line of a He-Ne laser (HRR120-1, Thorlabs, USA) was used to seed the system. The beam was spatially filtered, collimated and then incident on a transmissive liquid crystal-based twisted nematic spatial light modulator (SLM, LC- 2002, Holoeye Photonics, Germany, 600 × 800 square pixels, pixel dimension 32 μm). The grey levels of the individual SLM pixels were modulated using user controlled inputs of either mono or multifractal fluctuation series. Fractional Brownian motion algorithm was used to generate monofractal fluctuation series with user controlled Hurst exponent (H) and multifractal fluctuation series with user controlled generalized Hurst exponent h(q) was generated using binomial multifractal model (see Supplementary information). Electrical addressing of the SLM pixels allowed the setting of the grey levels of each pixel according to the synthesized fluctuation series. This was achieved by setting the grey level of the central SLM pixel as the first element of the synthesized fluctuation series, the second element was used to set grey levels of all the neighboring pixels which made a square envelop and so on. The SLM, acting as a synthetic mono/multifractal scattering (diffracting) object, was positioned at the front focal plane of the Fourier transforming lens (focal length f) and an EMCCD camera (iXon3-885, Andor Technology, UK, 1004 × 1002 square pixels, pixel dimension 8 μm) was at its back focal (Fourier) plane. The recorded intensity distribution at the CCD (x-y) plane represented the spatial frequency ( ) distribution of the mono/multifractal object (SLM).
) distribution of the mono/multifractal object (SLM).
References
Mandelbrot, B. The Fractal Geometry of Nature (W. H. Freeman, New York, 2000).
Feder, J. Fractals (Plenum Press, New York, 1988).
Segev, M., Soljačić, M. & Dudley John, M. Fractal optics and beyond. Nature Photon. 6, 209–210 (2012).
Stanley, H. Eugene. & Meakin, Paul. Multifractal phenomenon in physics and chemistry. Nature 335, 405–409 (1988).
Ivanov Plamen, Ch. et al. Multifractality in human heartbeat dynamics. Nature 399, 461–465 (1999).
Amaral, L. A. N. et al. Behavioral-independent features of complex heartbeat dynamics. Phys. Rev. Lett. 86, 6026–6029 (2001).
Lovejoy, S., Schertzer, D. & Stanway, J. D. Direct evidence of multifractal atmospheric cascades from planetary scales down to 1 km. Phys. Rev. Lett. 86, 5200–5204 (2001).
Argoul, F. et al. Wavelet analysis of turbulence reveals the multifractal nature of Richardson cascade. Nature 338, 51–53(1989).
Govindan, R. B. et al. Global climate models violate scaling of the observed atmospheric variability. Phys. Rev. Lett. 89, 0285011–0285014 (2002).
McAteer, R. T. J., Young, C. A., Ireland, J. & Gallagher, P. T. The bursty nature of solar flare X-ray emission. Astrophys. J. 662, 691 (2007).
Zunino, L. et al. A multifractal approach for stock market inefficiency. Physica A 387, 6558–6566 (2008).
Boustany, Nada. N., Boppart, Stephen. A. & Backman, Vadim. Microscopic imaging and spectroscopy with scattered light. Annu. Rev. Biomed. Eng. 12, 285–314 (2010).
Wax, A. & Backman, V. Overview of classical light scattering formalisms. in Biomedical Applications of Light Scattering (Wax A., & Backman V. Eds, McGraw Hill Publishing, 2009).
Tuchin, V. V., Wang, L. & Zimnyakov, D. À. Optical Polarization in Biomedical Applications (Springer-Verlag, 2006).
Nandan et al. Probing multifractality in tissue refractive index: prospects for precancer detection. Opt. Lett. 38, 211–213 (2013).
Kantelhardt, Jan. W. et al. Multifractal detrended fluctuation analysis of non-stationary time series. Physica A 316, 87–114 (2002).
Born, Max. & Wolf, Emil. Principles of Optics (Cambridge Univ. Press, Cambridge, England, 1999).
Hunter, M. et al. Tissue self-affinity and polarized light scattering in the Born approximation: A new model for precancer detection. Phys. Rev. Lett. 97, 138102 (2006).
Cherkezyan, L. et al. Interferometric spectroscopy of scattered light can quantify the statistics of sub diffractional refractive-index fluctuations. Phys. Rev. Lett. 111, 033903 (2013).
Çapoğlu İlker, R., Rogers,. Jeremy, D., Taflove, A. & Backman, V. Accuracy of the Born approximation in calculating the scattering coefficient of biological continuous random media. Opt. Lett. 34, 2679–2681 (2009).
Choi, W. et al. Tomographic phase microscopy. Nat. Methods 4, 717–719 (2007).
Xu, M. & Alfano, R. R. Random walk of polarized light in turbid media. Phys. Rev. Lett. 95, 213901 (2005).
Arifler, D., Pavlova, I., Gillenwater, A. & Richards-Kortum, R. Light scattering from collagen fiber networks: Micro-optical properties of normal and neoplastic stroma. Biophys. J. 92, 3260–3274 (2007).
Thekkek, Nadhi. & Richards-Kortum, Rebecca. Optical imaging for cervical cancer detection: solutions for a continuing global problem. Nature 8, 725–731(2008).
Bogenrieder, T. & Herlyn, M. Axis of evil: molecular mechanisms of cancer metastasis. Oncogene 22, 6524–6536 (2003).
Trimboli Anthony, J. et al. Pten in stromal fibroblasts suppresses mammary epithelial tumours. Nature 461, 1084–1093 (2009).
Acknowledgements
This work was supported by IISER-Kolkata, an autonomous institute funded by MHRD, Govt. of India. The authors thank Dr. Asha Agarwal, G.S.V.M. Medical College and Hospital, Kanpur, for providing the histopathologically characterized tissue samples. N.D. acknowledges CSIR, Govt. of India for research fellowship.
Author information
Authors and Affiliations
Contributions
N.G. designed and supervised this study; contributed in writing the manuscript, designing experimental strategies and theoretical models. N.D. and S.C. performed all the experiments (on tissues and control phantoms), analyzed data (both forward multifractal analysis on DIC images and inverse analysis on tissue light scattering data) contributed in writing the manuscript. A.V. and A.P. contributed in theoretical analysis/interpretation of data and in writing the manuscript. P.K.P. contributed in theoretical multifractal analysis, interpreting the data and writing the manuscript. S.K. contributed in the control validation studies on synthetic mono/multifractal scattering phantoms (both experiment and data analysis).
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Electronic supplementary material
Supplementary Information
Tissue multifractality and Born approximation in analysis of light scattering: a novel approach for precancer detection
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article's Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder in order to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Das, N., Chatterjee, S., Kumar, S. et al. Tissue multifractality and Born approximation in analysis of light scattering: a novel approach for precancers detection. Sci Rep 4, 6129 (2014). https://doi.org/10.1038/srep06129
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep06129
This article is cited by
-
Ultra-Sensitive Surface Plasmon Resonance Biosensor for Liver Metastases and Hepatocellular Carcinoma Detection Using Silicon Nitride and Black Phosphorus Nanomaterial
Plasmonics (2024)
-
Near-infrared refractive detection of newly freshly-excised human-liver tissues: an optical refractive index biosensor based on 2D-photonic crystal
Optical and Quantum Electronics (2023)
-
Fractal nature of groundwater level fluctuations affected by riparian zone vegetation water use and river stage variations
Scientific Reports (2019)
-
Visible to near-infrared refractive properties of freshly-excised human-liver tissues: marking hepatic malignancies
Scientific Reports (2016)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.