Abstract
The compartmental models used to study epidemic spreading often assume the same susceptibility for all individuals and are therefore, agnostic about the effects that differences in susceptibility can have on epidemic spreading. Here we show that–for the SIS model–differential susceptibility can make networks more vulnerable to the spread of diseases when the correlation between a node's degree and susceptibility are positive and less vulnerable when this correlation is negative. Moreover, we show that networks become more likely to contain a pocket of infection when individuals are more likely to connect with others that have similar susceptibility (the network is segregated). These results show that the failure to include differential susceptibility to epidemic models can lead to a systematic over/under estimation of fundamental epidemic parameters when the structure of the networks is not independent from the susceptibility of the nodes or when there are correlations between the susceptibility of connected individuals.
Similar content being viewed by others
Introduction
The contact networks that underlie the spread of diseases, behaviors1 and ideas have heterogeneous topologies2,3,4, but also, exhibit heterogeneity in the susceptibility of individuals7,8,9,10,11. In recent years the compartmental models used to study the spread of behaviors have been generalized to include the effects of network topology, but not the effects of both topology and differences in the susceptibility of individuals4,12,13. Generalizations including the network topology have revealed an intimate connection between the spectral properties of the contact network and the basic reproductive number of infectious diseases, showing that for a network described by an arbitrary degree distribution the basic reproductive number of an infection (R0), is proportional to the largest eigenvalue of the contact network's adjacency matrix13. For highly heterogeneous networks, this eigenvalue is always larger than 1 meaning that network heterogeneity can reduce and even eliminate the existence of an epidemic threshold.
Our understanding of the role of heterogeneous network topologies in epidemic spreading, however, has not been matched by a comparable development in our understanding of the role of heterogeneity in the susceptibility of individuals. Yet, differential susceptibility, defined as the variation in the susceptibility of individuals is as widespread as network heterogeneity. For example, genetic conditions are known to cause heterogeneous reactions to HIV7,8, H5N1 influenza9 and the Encephalomyocarditis virus10. Differential susceptibility can also be the result of differences in age as it has been shown in the case of Hantaan Virus in mice11. Other mechanisms leading to differential susceptibility include previous disease history, obesity, stress, history of drug abuse, physical trauma or differences in healthcare quality, which could emerge from discriminatory practices or individual self-selection. The biological prevalence of differential susceptibility, therefore, invites us to ask whether relaxing the assumptions of homogeneous susceptibility has consequences for the spread of epidemics that are tantamount to the relaxation of assumptions of homogeneity in the connectivity of the contact network.
The incorporation of differential susceptibility into epidemic models, however, also introduces a new dimension to epidemic modeling, since there are multiple ways for individuals with differences in susceptibility to be arranged in a network. For instance, the mixing patterns and segregation of populations14 imply that differential susceptibility can be structured through non-trivial correlations. Examples here include schools, nursing homes and hospitals, where children, senior citizens and patients, who can be more susceptible to diseases, spend more time together. These mixing patterns imply that a complete study of differential susceptibility should consider not only variations in the susceptibility of individuals, but also the correlations between the susceptibility of individuals and the positions these occupy in a network.
Understanding how epidemic spreading is affected by differential susceptibility can affect a number of policy decisions, since epidemic models do not only inform the spread of infectious diseases, but also the spread of behaviors15, such as smoking16; health conditions, such as obesity1; and digital threats, such as computer and mobile phone viruses17. Here, however, we show that the failure to consider differences in the susceptibility of individuals can lead to over- or underestimate a network's vulnerability to epidemic spreading.
In this paper we solve the SIS epidemic model for a contact network with arbitrary network topology and differential susceptibility and show that its basic reproductive number R0 is proportional to the maximal eigenvalue of a topology-infection matrix that combines information on the topology of the network and the susceptibility of individuals. Using mean-field theory, we look at individual level correlations between the susceptibility and the degree or connectivity of individuals and show that positive correlations between susceptibility and degree makes the network more vulnerable to epidemics (increasing R0), whereas negative correlations make the network less vulnerable (decrease R0). Finally we look at segregation by studying the consequences of having individuals connected to other individuals with similar characteristics and show that segregation significantly increases the vulnerability of the network to disease – causing R0 to increase. To conclude, we illustrate the strong effects of segregation dynamics on R0 by running a variant of Schelling's segregation process19 on a real-world contact network obtained from face-to-face proximity between students and teachers. This shows then even a mild level of segregation can drastically increase the critical reproductive number in a network where individuals differ in their susceptibility.
Results
The basic reproductive number R0 in the SIS model
We begin by summarizing the main results for the SIS model in heterogeneous networks without differential susceptibility. This will help us introduce the methodology and notation that we will use later and will also help us compare known results with those obtained for networks when differential susceptibility is present.
In the SIS model individuals can exist in either of two possible states: “healthy” or “infected”. Healthy individuals are infected when they come into contact with an infected individual with probability β. Infected individuals, on the other hand, become once again susceptible with a recovery probability δ. When each individual is in contact with k others, the basic reproductive number of a homogeneous network takes the form:

where the superscript h is used to indicate a homogeneous network.  can be interpreted as the average number of new infections that an infected individual generates during his infective period in a fully susceptible population. R0 is the quintessential epidemiological parameter, since the infection can only spread when an infected individual gives rise to one or more new infected (R0 > 1). Because of this, a central question in epidemiology is under what conditions R0 becomes greater than 1.
can be interpreted as the average number of new infections that an infected individual generates during his infective period in a fully susceptible population. R0 is the quintessential epidemiological parameter, since the infection can only spread when an infected individual gives rise to one or more new infected (R0 > 1). Because of this, a central question in epidemiology is under what conditions R0 becomes greater than 1.
In degree heterogeneous networks with no degree-degree correlations and a degree distribution given by P(k) the basic reproductive number R0 generalizes to3,4

where the superscript unc stands for uncorrelated networks, 〈k〉 is the average degree of the contact network, 〈k2〉 is the average of the degrees squared and σk is the standard deviation of the degree distribution. Note that when there is no heterogeneity, equation (2) reduces to equation (1), otherwise  since 〈k2〉 > 〈k〉2. In fact, for highly heterogeneous networks, where the degree distribution follows a power-law P(k) ∝ k−α with α < 3, σk (and therefore R0) grows with the network size, implying that the epidemic threshold vanishes for infinitely large networks (R0 is always larger than 1). It is worth noting that this result was obtained using the heterogeneous mean-field (HMF) theory, which neglects both dynamical and topological correlations. In HMF theory, the actual quenched structure of the network given by its adjacency matrix Aij is replaced by an annealed version, in which edges are constantly rewired at a rate much faster than that of the epidemics, while preserving the degree distribution P(k)5.
since 〈k2〉 > 〈k〉2. In fact, for highly heterogeneous networks, where the degree distribution follows a power-law P(k) ∝ k−α with α < 3, σk (and therefore R0) grows with the network size, implying that the epidemic threshold vanishes for infinitely large networks (R0 is always larger than 1). It is worth noting that this result was obtained using the heterogeneous mean-field (HMF) theory, which neglects both dynamical and topological correlations. In HMF theory, the actual quenched structure of the network given by its adjacency matrix Aij is replaced by an annealed version, in which edges are constantly rewired at a rate much faster than that of the epidemics, while preserving the degree distribution P(k)5.
In most real world networks nodes are not connected randomly to other nodes and this effect is characterized by what is known as non-trivial mixing patterns14. In the case of degree heterogeneity these mixing patterns are captured by the conditional probability P(k′|k) that a link starting at a node with degree k will end at a node with degree k′. In this case, the basic reproductive number takes the form12

where λ1,C is the largest eigenvalue of the degree mixing matrix Ckk′ = kP(k′|k).
While HMF theory assumes annealed networks, its validity for real (quenched) networks is limited6. Quenched networks are static, given by the adjacency matrix A, where aij = 1 if there is a link connecting node i to node j and 0 otherwise. A significant improvement over the HMF theory is given by the quenched mean-field (QMF) theory where it has been shown that the basic reproductive number takes the form13:

where λ1,A is the largest eigenvalue of the matrix A.
Differential susceptibility
Next, we introduce differential susceptibility by assuming that the susceptibility probability βi is different for each node i in the network. To further clarity, we consider βi in terms of the probability that a susceptible individual i gets infected when in contact with an infected individual.
After taking this consideration into account we proceed by following Wang et al.13 and note that for an arbitrary network topology given by an irreducible non-negative adjacency matrix A = [aij]N×N, the evolution of the SIS model can be written following as:

where pi(t) is the expected probability that node i will be infected at time t and fi(t) is the probability that node i receives the infection from at least one of its infected neighbors at time t. The probability fi(t) has the form:

Equation (5) is a non-linear dynamical system in which the case of no infection in the network (pi = 0, i ∈ {1, …, N}) represents a fixed point of the system that becomes unstable when R0 > 1. To test for asymptotic stability, we linearize the system (5) around p = 0 by removing all higher-order terms of pi(t):

We note that here we have assumed no differences in the recoverability rate of individuals (i.e. delta is constant). Next, we express (7) in matrix form as:

where M = [mij], mij = βiaij + Δij(1 − δ) and Δij is the Kronecker delta. Thus, one gets that the state with no disease is asymptotically stable if the largest eigenvalue of M, λ1,M < 1.
We note that when the origin is asymptotically stable, it is also globally stable, since

where the second inequality follows directly from the Weierstrass product inequality. Using this, we see that the system satisfies the inequality

Thus, when λ1,M < 1, the infection will die out exponentially fast with a rate determined by λ1,M.
Solutions with incomplete information
The connection between the largest eigenvalue of M (λ1,M) and the epidemic threshold represents a solution of the system that has little practical use in absence of complete information about the network topology and the susceptibility of individuals. For the model to be of practical use we need to estimate λ1,M when there is incomplete information about the topology of the network and/or the distributions of susceptibility probabilities of individuals. First, we note that the matrix M = R + (1 − δ)I where R = [rij], rij = βiaij and I is the identity matrix. Therefore, we can define the threshold at which epidemics begin to spread through the largest eigenvalue of R and generalize R0 in equation (4) to:

To estimate λ1,R when there is incomplete information about the system, we assume that rij is a random variable following an arbitrary distribution and use a mean-field approximation rij ≈ 〈rij〉 where 〈rij〉 is the expected value of rij over all possible network realizations. In a network where the susceptibility βi is assigned independently of the topology, we have that 〈rij|aij〉 = 〈β|aij〉 aij = 〈β〉 aij where 〈x|y〉 is the expected value of x given y. Then we obtain the basic reproductive number

In the case of uncorrelated networks with heterogeneous degrees, we relax 〈rij〉 to the expected number of links between nodes i and j, which is proportional to the product of the degrees of i and j. Keeping arbitrary susceptibility probabilities and degrees, we have

Since R is an irreducible matrix, the eigenvector v associated with the maximal eigenvalue λ1,R is strictly positive. Additionally, there are no other positive eigenvectors except positive multiples of v. In this case, using the positive eigenvector v = [vi] with vi = kiβi, one immediately obtains the maximal eigenvalue and therefore the basic reproductive number

where −1 ≤ ρ ≤ 1 is the Pearson correlation coefficient between the susceptibility βi and the square of the degree ki of individuals, 〈β〉 and 〈k2〉 are their respective averages and σβ and  are their respective standard deviations. Looking at equation (14), we point out that even small correlations between the susceptibility and the degree can lead to significant over- or underestimation of R0 when the variation in connectivity, as measured by
are their respective standard deviations. Looking at equation (14), we point out that even small correlations between the susceptibility and the degree can lead to significant over- or underestimation of R0 when the variation in connectivity, as measured by  , is large compared to the average connectivity 〈k〉, which is the for networks following a heterogeneous degree distribution.
, is large compared to the average connectivity 〈k〉, which is the for networks following a heterogeneous degree distribution.
Networks with non-trivial mixing patterns
We now focus on link level correlations, where the tendency of individuals to connect to other individuals with similar characteristics leads to non-trivial mixing patterns. We note that the same mathematical procedure can be used for the analysis regardless of whether we have correlations in susceptibility and constant recovery probability or vice versa. We consider link level correlations in the degree and the susceptibility of nodes. Then we approximate rij with 〈rij〉, by using the expected number of links from node with degree ki and susceptibility βi to node with degree kj and susceptibility βj. The expected number of links are proportional to the two-point conditional probability P(k′, β′|k, β):

To find the maximal eigenvalue of the matrix R as defined by equation (15) we need to find a positive vector v = [vi] such that

holds for all i. Using some algebraic manipulations, we can rewrite equation (16):

which holds for every i. Writing  and summing these N equations over i where ki = k and βi = β, we have
and summing these N equations over i where ki = k and βi = β, we have

which holds for every combination of k and β. We can simplify equation (18) further by writing  :
:

where λ1,D is the maximal eigenvalue of the matrix D{k,β}, {k′,β′} = kβP(k′, β′|k, β). In other words, the matrices R and D share the same maximal eigenvalue. So, we will use λ1,D as an approximation of the actual R0 when there is limited information in the network:

Assuming d = |{k, β}| is the number of different combinations of degree (k) and susceptibility (β) that a node can have in the network, we have compressed the entire information about the system (network topology and the susceptibilities of nodes) into a coarsened d × d matrix. In fact, we can choose d depending on how much information we have about the network. For example, we can assign each individual to one of 5 degree classes, k = 1, 2, 4, 8, 16 and to one of 3 susceptibility classes, β = βlow, βavg, βhigh corresponding to low, average and high susceptibility respectively. We then only need to estimate the mixing patterns P(k′, β′|k, β) between the 15 classes of individuals, as opposed to knowing every entry in the matrix R. The more classes we have, the more mixing patterns we have to estimate and the closer λ1,D will be to the actual λ1,R.
Moreover, if we assume independence between the degree of a node and its susceptibility, i.e. P(k′, β′|k, β) = P(k′|k)P(β′|β) and choose  where
where  and
and  are the positive eigenvectors corresponding to the maximal eigenvalues λ1,C and λ1,B of the matrices Ckk′ = kP(k′|k) and Bββ′ = βP(β′|β) respectively, we can simplify equation (19):
are the positive eigenvectors corresponding to the maximal eigenvalues λ1,C and λ1,B of the matrices Ckk′ = kP(k′|k) and Bββ′ = βP(β′|β) respectively, we can simplify equation (19):

which gives λ1,R = λ1,Cλ1,B and solves the system of equations. Note that when there is no degree mixing, λ1,C = 〈k2〉 / 〈k〉. On the other hand, when there are no mixing patterns in susceptibility, λ1,B = 〈β〉.
Equation (19) allows us to estimate the basic reproductive number at different granularity depending on how much information we have about the network topology and the distribution of susceptibilities. However, from the scientific perspective it is still unclear how the different mixing patterns impact the spread of diseases. To push our understanding of the effect of differential susceptibility further we study the effects of segregation in the spread of diseases.
Segregation
Since the contact networks that underlie the spread of a disease are not only heterogeneous in terms of degree and susceptibility, but also segregated, we next proceed to solve the model for the cases where individuals are more likely to connect with others a similar level of susceptibility. As we will see, segregation can have an impact in the spreading of a disease that goes beyond the effects of differential susceptibility.
To understand the effect of segregation, we focus on the case where the degree of a node is independent of its susceptibility, λ1,R = λ1,Cλ1,B and look respectively, at the limiting cases when there is no segregation and maximal segregation. Note that in the case of no segregation P(β′|β) = P(β′) and the largest eigenvalue of B is λ1,B = 〈β〉 (with eigenvector v, vβ = β), hence the basic reproductive number takes the form

On the other hand, in the case of maximal segregation, where nodes only share links with nodes with the same susceptibility, B is diagonal with β's as the diagonal elements. In this case, λ1,B is equal to the largest susceptibility in the system βmax. Thus, in the case of maximal segregation, the basic reproductive number becomes

We note that in this extreme case nodes do not share links outside their susceptibility class, so the network is made of disconnected components. Hence, R0 > 1 implies a persistent infection in at least one of these components. We do want to stress that in general R0 > 1 does not guarantee a macroscopic outbreak in the network, but the existence of a highly vulnerable pocket, or subgraph, where R0 is above 1. In this case, the epidemic will be persistent, but will most likely remain contained.
To obtain general bounds for  , we use the Collatz-Wielandt formula20, which states that the Perron root of a matrix A is given by r = maxv∈Ωf(v), where
, we use the Collatz-Wielandt formula20, which states that the Perron root of a matrix A is given by r = maxv∈Ωf(v), where

Similarly, the min-max version states that r = minv∈Ωf(v) where

We rewrite the min-max and max-min versions of the Collatz-Wielandt formula into a form that we will use in the rest of the paper

which holds for all non-negative non-zero vectors v. Assuming the matrix B is irreducible, the Perron root of B coincides with the largest eigenvalue λ1,B. Thus, using equation (26), we can bound λ1,B

where v = [vβ] can be any non-negative vector. Choosing the vector v such that vβ = β in equation (27), we immediately obtain the bound:

where 〈β|β′〉 denotes the average susceptibility of the individuals connected to an individual with susceptibility β′. These bounds provide useful information to understand the potential impact of a disease under limited knowledge about the network topology. We note that weak segregation limits the variation of 〈β|β′〉 across the different susceptibility classes bounding R0 in a small region around 〈β〉. Strong segregation on the other hand, increases the gap between the bounds and our uncertainty for R0.
To extend our intuition further we consider a simple network model with tunable segregation. Here, each node has the same degree 〈k〉 and P(β′|β) = (1 − s)/Nβ and P(β|β) = (1 − s)/Nβ + s where Nβ is the number of different susceptibility classes and s ∈ [0, 1] models the segregation in the network. When s = 0, P(β′|β) = 1/Nβ = P(β|β) and the chances that a node will connect to others is independent of the susceptibility β. When, s = 1, segregation is maximal (P(β|β) = 1 and P(β′|β) = 0) and nodes share links only with others that have the same susceptibility. In this model, R0 = λ1,Cλ1,B + 1 − δ = 〈k〉 λ1,B + 1 − δ since all nodes have the same degree 〈k〉. To derive bounds for R0 in this segregation model, we note that P(β′|β) = (1 − s)/Nβ + Δββ′s where Δββ′ is the Kronecker delta. Putting this into equation (27) we have

Then choosing vβ = βP(β) and using the fact that P(β) = 1/Nβ we have

On the other hand, the lower bound for λ1,B has the form

where again v = [vβ] can be any non-negative vector. Note that if we choose vβ = 1 if β = βmax and 0 otherwise, we get the lower bound

Thus, we obtain the bounds for the basic reproductive number:

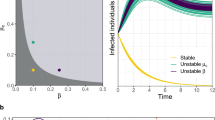
Fig. 1a shows the basic reproductive number R0 as a function of the amount of segregation s (solid line) along with the bounds given by equation (33) (dashed lines). We observe that as the amount of segregation increases, the network develops a highly susceptible pocket and R0 tends to 〈k〉 βmax + 1 − δ. This increase in vulnerability comes from highly susceptible groups of individuals that provide a stable pocket supporting the infection. The results show that segregation makes the network of individuals only as strong as its weakest subgroup. This suggests an immunization strategy that seeks to identify and target clusters of highly susceptible individuals, instead of groups of highly susceptible individuals that are connected to others that are less susceptible.
Impact of segregation on R0.
(a) R0 = λ1,B 〈k〉 + 1 − δ as a function of the amount of segregation s (solid line) along with the bounds given by equation (33) (dashed lines) with Nβ = 5 susceptibility classes uniformly spaced between [0.005, 0.025] with 〈β〉 = 0.015. Additionally, to compute an actual value for R0 a degree k = 25 and δ = 0.5 was assumed. (b) R0 = λ1,R (solid line) and the approximation R0 ≈ λ1,D (dashed line) for the face-to-face proximity school network for different iterations of the segregation process.
To illustrate the effects of segregation, we look at a real-world contact network of face-to-face proximity between students and teachers in a primary school18. Links between A and B denote the cumulative time spent by A and B in face-to-face proximity, over one day. For simplicity, we convert this daily network to an unweighted network by assigning a link between the pair of nodes that have spent more than 2 minutes of cumulative time in face-to-face proximity. After discretizing the links, we keep the largest connected component which consists of 225 nodes. We then run a variation of the Schelling's segregation process19 where initially each node is randomly assigned to one of two susceptibility classes. We use δ = 0.5 and assign high susceptibility nodes βhigh = β1 and low susceptibility nodes with β = β1/10, thus having only one parameter in the network, β1. To segregate this initial network, we assign to each node i a potential energy |βi − 〈β〉i| where 〈β〉i is the average susceptibility of i's neighboring nodes. At each iteration, we swap a random pair of nodes if this decreases the total potential energy in the network. With each new iteration, we conserve the distribution of total susceptibility in the network but increase the level of segregation. Fig. 1b shows the increase of R0 = λ1,R (solid line) with iterations of Schelling's segregation process. The dashed line on the other hand shows the approximation R0 ≈ λ1,D when there is limited information in the network. The matrix D is constructed by coarse-graining the network into 7 degree classes k = {1, 2, 4, 8, 16, 32, 64} where each node is assigned to its nearest degree class and two susceptibility classes β = {β1, β1/10}. It is worth mentioning that we compute λ1,D by estimating only 142 entries of the matrix D, as opposed to the 2252 entries of the matrix R, which is a significant reduction in the amount of information we need about the system.
Fig. 2a, 2b and 2c show the primary school network at three different iterations in the segregation process; no segregation, mild segregation and high segregation respectively, with high susceptibility nodes colored red. Fig. 2d shows the average fraction of infected nodes in the endemic state, ρ, averaged over 10, 000 simulations, for different values of β1 for the three networks shown in Fig. 2a, b and c. As we mentioned earlier and as can be seen in Fig. 2d, segregation can change the shape of the epidemic curve and depending on the network topology, high R0 does not necessarily lead to a high number of infected nodes in the endemic state. This can happen when there is extreme segregation and the infection is contained within a small number of highly susceptibility nodes that have no or little contact to the rest of the network. In practice, however, we often observe mild segregation which increases both R0 and the number of infected nodes in the endemic state. Finally, we compute the critical values of β1 using equation (11). The inset of Fig. 2d shows ρ near these critical values along with the critical values (horizontal dashed lines).
The endemic state for different level of segregations and different susceptibility.
(a), (b) and (c) face-to-face proximity school network with no, mild and high segregation respectively. High susceptibility nodes are colored red. d) The fraction of infected nodes in the endemic state averaged over 10,000 runs as a function of the susceptibility β1 for the school network with three levels of segregation, along with the critical values of β1 for which R0 = λ1,R + 1 − δ = 1 (inset) denoted as horizontal dashed lines.
Discussion
In this paper, we extended the SIS model to incorporate heterogeneous susceptibility and showed that heterogeneity can significantly increase the networks' vulnerability to diseases. For individual level correlations between the susceptibility and the degree of a node, we find that approaches using the average susceptibility of the system to approximate R0 will over- or underestimate the potential spread of diseases. In other words, when there is variation in susceptibility, the increase in susceptibility of a few individuals is not necessarily compensated by the decrease in susceptibility of others, since the degrees and locations of these individuals play an important role. On the other hand, we found that when nodes with similar characteristics are more likely to be connected, the vulnerability of the network increases, since a small group of densely connected high-susceptible individuals can act as a pocket supporting a persistent infection. Having a formula to compute R0, however, has little practical use in absence of complete information about the network topology and the distribution of susceptibilities. In this case, we provided a method to approximate R0 by coarse-graining the individual nodes into degree-susceptibility classes and only estimating the mixing patterns between these classes. Going forward, it is important that mathematical models of epidemic spreading include the effects of heterogeneous susceptibility to provide more accurate descriptions of epidemic spreading processes. Otherwise, the basic reproductive numbers estimated from compartmental models will be systematically over or underestimated.
References
Christakis, N. A. & Fowler, J. H. The spread of obesity in a large social network over 32 years. N. Engl. J. Med. 357, 370–379 (2007).
Albert, R. & Barabási, A. L. Statistical mechanics of complex networks. Rev. Mod. Phys. 74, 47–97 (2002).
Anderson, R. M., May, R. M. & Anderson, B. Infectious diseases of humans: dynamics and control. (Oxford university press, Oxford, 1992).
Pastor-Satorras, R. & Vespignani, A. Epidemic spreading in scale-free networks. Phys. Rev. Lett. 86, 3200–3203 (2001).
Boguna, M., Castellano, C. & Pastor-Satorras, R. Langevin approach for the dynamics of the contact process on annealed scale-free networks. Phys. Rev. E 79, 036110 (2009).
Boguna, M., Castellano, C. & Pastor-Satorras, R. Nature of the Epidemic Threshold for the Susceptible-Infected-Susceptible Dynamics in Networks. Phys. Rev. Lett. 111, 068701 (2013).
Hardie, R. et al. Human leukocyte antigen-dq alleles and haplotypes and their associations with resistance and susceptibility to hiv-1 infection. AIDS 22, 807–816 (2008).
Li, J., Liu, Y., Kim, T., Min, R. & Zhang, Z. Gene expression variability within and between human populations and implications toward disease susceptibility. PLoS Comput. Biol. 6, e1000910 (2010).
Boon, A. C. M. et al. H5n1 influenza virus pathogenesis in genetically diverse mice is mediated at the level of viral load. MBio 2, e00171-11 (2011).
Friedman, S. B., Grota, L. J. & Glasgow, L. A. Differential susceptibility of male and female mice to encephalomyocarditis virus: effects of castration, adrenalectomy and the administration of sex hormones. Infect. Immun. 5, 637–644 (1972).
Nakamura, T., Yanagihara, R., Gibbs, C., Amyx, H. & Gajdusek, D. Differential susceptibility and resistance of immunocompetent and immunodeficient mice to fatal hantaan virus infection. Arch. Virol. 86, 109–120 (1985).
Boguna, M. & Pastor-Satorras, R. Epidemic spreading in correlated complex networks. Phys. Rev. E 66, 047104 (2002).
Wang, Y., Chakrabarti, D., Wang, C. & Faloutsos, C. Epidemic spreading in real networks: An eigenvalue viewpoint. In: 22nd International Symposium on Reliable Distributed Systems (SRDS'03), 25–34. IEEE Computer Society, Los Alamitos, CA, USA (2003).
Newman, M. E. J. Mixing patterns in networks. Phys. Rev. E 66, 026126 (2003).
Centola, D. & Macy, M. Complex contagions and the weakness of long ties. Am. J. Sociol. 113, 702–734 (2007).
Christakis, N. A. & Fowler, J. H. The collective dynamics of smoking in a large social network. N. Engl. J. Med. 358, 2249–2258 (2008).
Wang, P., Gonzalez, M. C., Hidalgo, C. A. & Barabási, A. L. Understanding the spreading patterns of mobile phone viruses. Science 324, 1071–1076 (2009).
Stehlé, J. et al. High-resolution measurements of face-to-face contact patterns in a primary school. PloS one 6, e23176 (2011).
Schelling, T. Dynamic models of segregation. J. Math. Sociol. 1, 143–186 (1971).
Meyer, C. Perron-frobenius theory of nonnegative matrices. Matrix analysis and applied linear algebra. 666–667 (SIAM, Philadelphia, PA, 2000).
Acknowledgements
L.K. thanks ONR Global, project “Information fusion in networked sensors and systems”, for partial support. C.A.H. acknowledges the MIT Media Lab consortia and the ABC Career Development Chair.
Author information
Authors and Affiliations
Contributions
D.S., C.A.H. and L.K. designed the research. D.S. developed analytic tools and performed simulations. D.S., C.A.H. and L.K. wrote the paper, discussed results and reviewed the manuscript.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Rights and permissions
This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 3.0 Unported License. The images in this article are included in the article's Creative Commons license, unless indicated otherwise in the image credit; if the image is not included under the Creative Commons license, users will need to obtain permission from the license holder in order to reproduce the image. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-sa/3.0/
About this article
Cite this article
Smilkov, D., Hidalgo, C. & Kocarev, L. Beyond network structure: How heterogeneous susceptibility modulates the spread of epidemics. Sci Rep 4, 4795 (2014). https://doi.org/10.1038/srep04795
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep04795
This article is cited by
-
Characterizing tuberculosis transmission dynamics in high-burden urban and rural settings
Scientific Reports (2022)
-
A geometric analysis of the SIRS epidemiological model on a homogeneous network
Journal of Mathematical Biology (2021)
-
Sub-national variation in measles vaccine coverage and outbreak risk: a case study from a 2010 outbreak in Malawi
BMC Public Health (2018)
-
Dueling biological and social contagions
Scientific Reports (2017)
-
Disconnected, fragmented, or united? a trans-disciplinary review of network science
Applied Network Science (2016)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.