Introduction

Organization in nature is in the eye of the observer. Where many see randomness and nondeterminism, others see organization and principle1. Nowhere is this more evident than in the discussion of turbulence. In spite of their obvious irregular appearance, turbulent flows are united by “organization” that makes their behavior expected, predictable and reliable.

For example, measurements of flow friction inside pipes and on solid surfaces have been lining up on curves that science and technology has used with confidence for more than a century. The large scale structure of jets and plumes, have become evident when the methods of measuring and visualizing turbulence improved. This empirical body serves as skeleton for the computational models and software packages used today to simulate turbulent flows at all scales, all the way to atmospheric circulation and the weather.

The natural occurrence of organization is an integral part of the phenomenon of turbulence and it is calling for a summarizing principle. Progress was made in this direction based on the constructal law of design and evolution in nature2,3,4, which holds that flow systems in nature, animate and inanimate, exhibit the natural tendency to evolve into successive configurations that offer greater flow access over time. The constructal law was used to predict and unify the turbulence phenomena, for example, the transition to turbulence, the size of the smallest eddy, the large scale structure of jets and plumes and the correlations for friction and heat transfer. Reviews of these developments are available in Refs. 3–5.

Here we draw attention to a pattern of turbulent flow evolution that went unquestioned and shows how to predict it. The smoke from a row of closely spaced factory smoke stacks (or a brush fire) rises as a curtain, i.e. as a two-dimensional plume. It is only above a certain height that the curtain of smoke organizes itself into a round plume that, from a distance, looks like all the other plumes (e.g. Fig. 1). This observation is extremely common.

Figure 1
figure 1

Above a certain height, all turbulent plumes have round cross sections.

Top left: flat plume rising from a row of smoke stacks. Top middle: round plume rising from a concentrated fire. Top right: plume above a brush fire. Bottom: The coalescence of plumes above the steam power plant at Duke University. (Photographs made by Adrian Bejan).

Full size image

Why is this?

The reason is the natural tendency of flow systems to morph into configurations that facilitate the access to what flows. In jets and plumes, it is momentum that flows from the mover (the turbulent column) to the non-mover (the still surroundings). Momentum flows perpendicularly to the flow of fluid. This flow is called “mixing”, or momentum transfer. When the lateral flow of momentum has greater access to the stationary environment, the fluid of the column mixes faster with the surrounding fluid and its longitudinal speed decreases faster. The tendency of the flow is to morph its cross section such that the mixing becomes more effective and the longitudinal speed decreases faster.

Turbulent free jets issuing from noncircular slots or nozzles have been studied because they are used in technical areas ranging from aerospace to chemical to mechanical engineering, such as aircraft design, gas turbine combustors and cooling systems for turbine blades. For example, studies of free jets issuing from circular and noncircular nozzles documented the effect of the shape and size of the nozzle on jet development6,7,8. Other studies documented the velocity and temperature fields by using linearized hot-wire anemometers9,10,11,12. It is now established that there are three regions in the downstream direction of a three dimensional jet. The first is the potential core region, which contains the flow close to the jet exit with uniform longitudinal velocity, because mixing at the jet edges has not yet spread across the jet. Next is a region with decreasing longitudinal velocity that is dependent on nozzle configuration. This region bears the influence of the initial geometry of nozzle. Further downstream is an axisymmetric (round cross section) decay region, which contains axisymmetric flow that is independent of nozzle configuration13,14,15,16,17,18. Note the phenomenon that we identify, question and explain in this paper: the jet cross section evolves from nozzle-shaped to round, not the other way.

At bottom, the phenomenon explained in this paper adds to the growing evidence that the tendency toward evolutionary organization in nature is governed by a physics principle. In particular, the tendency toward round cross sections in simple (one stream) configurations unites the animate with the inanimate flow systems. Without exception, the cross sections tend to the round shape: blood vessels, pulmonary airways, subterranean rivers, large pores (“pipes”) in the hill slope, underground galleries of moles and earthworms, tunnels, intestines and many other features of animal design. In river channels, this natural tendency is made visible by the proportionality between depth and width in rivers of all sizes4,19.

Results

Turbulent plumes

Plumes are vertical jets driven by buoyancy due to heating from below (Fig. 1) or the density difference between a lighter fluid injected in a denser fluid. The methods and results on plumes and jets are classical, well known and not questioned in this paper. This is why they are relegated to the Supplement (for reviews see Refs. 5,20). Here the classical results are used in order to prove that the predicted evolutionary design from noncircular to circular flow cross sections is correct.

When the plume strength is large enough, the flow is turbulent. If the turbulent field is time averaged5, the flow occupies a mixing region the growth angle of which is approximately 20°. This rate of growth is a common feature of all turbulent mixing regions (shear layers, jets, plumes)5,20,21,22,23.

A two-dimensional turbulent plume fills a wedge, Fig. 2. The key scale is the vertical speed of the plume (cf. Supplement), v2 ~ [q′gβ/(ρcP)]1/3 where q′[W/m] is the strength of the heat source that drives the plume, g is the gravitational acceleration and β, ρ and cP are the coefficient of thermal expansion, density and specific heat at constant pressure.

Figure 2
figure 2

Turbulent plumes, flat (v2) vs round (v3).

The competition for more effective mixing (the smallest v) dictates the transition from flat plume to round plume (and not from round to flat).

Full size image

A round turbulent plume (Fig. 2) fills a three-dimensional volume shaped as a cone rising above a point heat source (e.g. concentrated fire) of strength q[W]. The vertical velocity (time averaged) along the plume centerline decreases with altitude (y) as v3 ~ [qgβ/(ρcPy)]1/3.

The comparison between v2 and v3 is shown in Fig. 2. The flow configuration that happens naturally is the configuration that offers better mixing with the ambient and this means that the two-dimensional plume must evolve upward into a round plume. Below a critical height, more effective mixing is offered by the two-dimensional plume, v2 < v3. Above that height, the more effective mixer is the round plume (v3 < v2). The height (ytr ~ L) where the transition occurs is predicted by intersecting v2 with v3. The transition height is of the same order as the larger length scale of the heat source that generates the two-dimensional plume and does not depend on the plume strength q.

Turbulent Jets

Consider a two-dimensional jet issuing at speed U0 from a slit of spacing D2 and width L (Fig. 3). The scale of its longitudinal velocity decreases as x−1/2 in the longitudinal direction, cf. Supplement, u2 ~ U0 [3γ2D2/(4x)]1/2, with γ2 = 7.67. If the nozzle is round with diameter D3 and velocity U0, the longitudinal velocity decreases as x−1, namely u3 ~ U0 [31/2γ3D3/(4x)], with γ3 = 15.2.

Figure 3
figure 3

Turbulent jets, flat (u2) and round (u3) and the transition from flat to round cross sections, in the direction of facilitating the momentum transfer from jet to ambient.

Full size image

The competition between u2 and u3 is shown in Fig. 3. Faster mixing occurs as the two-dimensional jet evolves into a round jet, not the other way around. The transition length is obtained by intersecting u2 with u3. The relation between D3 and D2 follows from the condition that the two jets must have the same strength at the nozzle, therefore . The distance xtr is proportional to the nozzle width L and does not depend on the jet strength or the nozzle Reynolds number, Re = U0D2/ν. This conclusion is similar to the result for plumes.

Laminar jets

The tendency to evolve from flat cross sections to round cross sections is also a characteristic of laminar jets, for which exact solutions exist in analytical form (cf. Supplement23,24), which are valid for Re > 1 when the jet region is slender and amenable to a boundary layer analysis. In the two-dimensional laminar jet the centerline velocity decreases as x−1/3 in the downstream direction, , where D2 and L are the dimensions of the slit, Fig. 3. In a round jet issuing from a nozzle of diameter D3, the centerline velocity decreases as . The intersection of the curves for u2 and u3 is qualitatively the same as in the lower graph of Fig. 3 and yields the transition distance , where we assumed that the two-dimensional jet has the same strength as the round jet. Unlike the transition lengths for turbulent flows, in the laminar jet the transition length xtr/L increases with the nozzle Reynolds number.

Discussion

In summary, the empirical formulas available for plumes and jets were used to test and confirm the theoretical prediction that the flow configuration should evolve from the flat cross section to the round cross section and not in the reverse direction over time. The transition from one configuration to the next was determined by intersecting the formulas available for the two types of cross-sectional shape, flat and round.

The same predictions were further tested against numerical experiments with flat jets in the Re range 10–104. With reference to the configuration shown at the top of Fig. 3, the jets issued from a slit with the ratio L/D2 = 10. The numerical formulation and software are described in Supplement. The simulations produced time-averaged velocity distributions through the entire flow field.

For each Re, the objective of one simulation was to document the evolution of the shape of the jet cross section with longitudinal position (x, collinear with u2 in Fig. 3) downstream from the nozzle. The cross section of the jet was defined in a constant-x cut as the area (A) enclosed by the loop along which the longitudinal velocity was equal to 1/2 of the centerline velocity. Samples of this conventional cross section are shown for Re = 500 in the upper frame of Fig. 4. Later, this conventional velocity was set equal to 1/4 of the centerline velocity, in order to verify that this convention has no effect on the conclusions regarding the transition from flat jet to round jet.

Figure 4
figure 4

The evolution of the cross-sectional shapes of turbulent jets in the range Re = 500–104 and laminar jets in the range Re = 10–30.

Full size image

The evolution of the shape of A was monitored by plotting the shape parameter defined here as p/A1/2, where p is the perimeter of A. When the cross section is flat, p/A1/2 is large, for example p/A1/2 = 22/101/2 ≅ 7 in the plane of the nozzle. When the cross sections are round, the shape parameter is small, p/A1/2 = 2π1/2 ≅ 3.5.

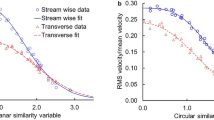
Figure 4 confirms the two parts of the theory. The transition from flat cross sections to shapes that are not flat occurs when x/L is of order 10. This is in accord with the theory, xtr ~ 9.6L. The shape in the transition range is not perfectly round. It oscillates once or twice between a horizontal ellipse and a vertical ellipse, however, as x/L increases the elliptical shape becomes progressively rounder. The second theoretical aspect is that the xtr/L value should not depend on Re. This is also confirmed by the variation of the shape parameter p/A1/2 versus x/L in the Re range 500–104.

Further support for the theory is provided by the lower graph of Fig. 4, which shows the corresponding results for laminar jets in the range Re = 10–30. The transition from flat to round jets is in accord with the theory, xtr,lam ~ 0.17 Re. For example, the predicted xtr/L for Re = 10 is of order 1, in accord with the x/L location of the elbow in the Re = 10 curve. For laminar jets, the predicted xtr/L should increase in proportion with Re. This is also confirmed by the results of Fig. 4. The elbows of the curves migrate to the right by a factor of 3 on the logarithmic abscissa, while the Re values increase by the same factor.

Conclusion

In this paper we used a common example of natural organization in order to demystify the phenomenon of evolution in nature. The example was inanimate: the evolution of all plumes and jets in one direction in time, from any cross-sectional shapes to round cross sections. The arrow of time points in one direction and this direction is captured by the constructal law of design evolution in nature.

The choice to illustrate evolution with an inanimate flow was intentional, because the prevalent view is that evolution is a phenomenon of biology and that it cannot be witnessed in our lifetime. We showed that in plumes and jets we see evolution in real time. We also see the principle that allows us to predict turbulence as a phenomenon of physics. The constructal law was used earlier5 to predict the laminar-turbulent flow transition, the transition from splat to splash as a liquid droplet hits a wall, the dendritic architecture of the snowflake, river basins and lightning trees. It can be used to predict the structure of two-phase jets25,26.

In sum, evolution is a universal phenomenon that unites the animate and inanimate flow designs of nature. Evolution unites biology with physics. In the human realm of life (movement) on the globe, this universal phenomenon is visible as technology evolution, science evolution, language, writing, the rule of law (government) and civilization. All forms of evolving organization obey the arrow of time27 illustrated in this paper.