Abstract
The steady boundary layer flow and heat transfer of a nanofluid past a nonlinearly permeable stretching/shrinking sheet is numerically studied. The governing partial differential equations are reduced into a system of ordinary differential equations using a similarity transformation, which are then solved numerically using a shooting method. The local Nusselt number and the local Sherwood number and some samples of velocity, temperature and nanoparticle concentration profiles are graphically presented and discussed. Effects of the suction parameter, thermophoresis parameter, Brownian motion parameter and the stretching/shrinking parameter on the flow, concentration and heat transfer characteristics are thoroughly investigated. Dual solutions are found to exist in a certain range of the stretching/shrinking parameter for both shrinking and stretching cases. Results indicate that suction widens the range of the stretching/shrinking parameter for which the solution exists.
Similar content being viewed by others
Introduction
The study of boundary layer flow and heat transfer over a stretching sheet has gained vast interest among researchers due to its various applications in industrial and engineering processes for example in manufacture and extraction of polymer and rubber sheets. Since then, various aspects of stretching sheet problems have been investigated by several researchers (see Kumaran et al.1, Hayat et al.2, Ishak et al.3, Mahapatra et al.4, Fang et al.5, Makinde and Aziz6, Rana and Bhargava7, Mahmoud and Megahed8, Rahman and Eltayeb9, Khan and Shahzad10, Mukhopadhyay11 etc.). It is well known that Khan and Pop12 presented the first paper on stretching sheet in a nanofluid.
Since the past few years, much interest was focused on convective heat transfer in a nanofluid. The base fluids such as water, oil and ethylene glycol used in many industrial processes such as in power generation, chemical processes and heating or cooling processes are poor heat transfer fluid due to its poor heat transfer properties with low thermal conductivity. One can improve this by suspending the solid nanoparticle into the base fluid in order to increase the thermal conductivity. According to Daungthongsuk and Wongwises13, the poor heat transfer properties of the base fluids was identified as a major obstacle to the high compactness and effectiveness of heat exchangers. The essential initiative is to seek the solid particles having thermal conductivities several hundreds of times higher than those of base or conventional fluids. It seems that Choi14 was the first to call the mixture of the base fluids with the solid nanoparticle as nanofluid. It was reported that nanofluids have good stability and rheological properties, dramatically higher thermal conductivities and no penalty in pressure drop (see Daungthongsuk and Wongwises13). A comprehensive literature on the topic of nanofluid has been discussed in the book by Das et al.15 and in the papers by, Kakaç and Pramuanjaroenkij16, Wong and De Leon17, Saidur et al.18, Fan and Wang19 and very recently by Jaluria et al.20 and Mahian et al.21.
Different from the above investigations, there are also many research articles on convective flow and heat transfer due to a shrinking sheet in recent years. Physically, there are two conditions where the flow towards a shrinking sheet is likely to exist, first, imposing an adequate mass suction on the boundary (Miklavčič and Wang22) and second, consider a stagnation flow (Wang23). It was reported that the analytical solutions on the viscous flow over a shrinking sheet with suction effects were first reported by Miklavčič and Wang22. It was observed that mass suction is necessary to maintain the flow within the boundary layer. After the earlier work by Miklavčič and Wang22, the study of flow due to a shrinking sheet was extended to other types of fluid (see Hayat et al.24 and Sajid et al.25). Since then, various aspect of flow and heat transfer due to a shrinking sheet has been investigated by researchers26,27,28,29,30,31,32. The case of unsteady flow towards a shrinking sheet was investigated by Bachok et al.33, Rohni et al.34, Fang et al.35 and Zheng et al.36. However, only a small amount of works were considered the flow and heat transfer characteristics due to a nonlinearly stretching or shrinking sheet (Rana and Bhargava7, Vajravelu37 and Cortell38).
In the present study, we investigate numerically the flow and heat transfer over a nonlinearly shrinking sheet immersed in a nanofluid with suction effect at the boundary. The present study is the extension of Rana and Bhargava7, to the case of shrinking sheet with suction effect. Numerical solutions are obtained using a shooting method. The effects of suction, thermophoresis, Brownian motion and stretching/shrinking parameters on the velocity, concentration and temperature profiles as well as heat transfer characteristics are graphically presented and discussed.
Problem formulation
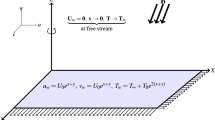
Consider a steady, laminar, incompressible and two dimensional boundary layer flow and heat transfer of a viscous nanofluid past a permeable stretching/shrinking sheet coinciding with the plane y = 0 and the flow being confined to y > 0. It is assumed that the pressure gradient and external force are neglected in this problem. The flow is generated by the nonlinear stretching/shrinking sheet along the x-axis where x is the coordinate measured along the stretching/shrinking sheet. Under the boundary layer approximations, the governing equations for conservation of mass, momentum, thermal energy and nanoparticle concentration of this problem can be expressed as (see Rana and Bhargava7, Khan and Pop12 and Buongiorno39)




The boundary conditions of Eqs. (1)–(4) are

where u and v are the velocity components in the x and y directions, respectively, T is the temperature, C is the nanoparticle volume fraction, Tw is the surface temperature, T∞ is the ambient temperature, Cw the nanoparticles volume fraction at the plate and C∞ is the nanoparticles volume fraction far from the plate, vw is the suction or injection velocity with vw < 0 for suction and vw > 0 for injection, τ = (ρc)p/(ρc)f, where (ρc)p is the effective heat capacity of the nanoparticles, (ρc)f is the heat capacity of the base fluid, α = km/(ρc)f is the thermal diffusivity of the fluid, ν is the kinematic viscosity, DB is the Brownian diffusion coefficient, DT is the thermophoretic diffusion coefficient and λ is the stretching/shrinking parameter with λ > 0 for a stretching surface and λ < 0 for a shrinking surface. The constant n is the nonlinearity parameter with n = 1 for the linear case and n≠1 is for the nonlinear case. It is assumed that the surface is stretched or is shrunk with the velocity Uw = axn, where a > 0 is a constant.
Further, we seek for a similarity solution of Eqs. (1)–(4) subject to the boundary conditions (5) by introducing the following similarity transformation7:

where prime denotes differentiation with respect to η. To have similarity solutions of Eqs.(1)–(5), we assume

where the constant parameter S corresponds to suction (S > 0) and injection (S < 0) or withdrawal of the fluid, respectively.
Substituting Eq. (6) into Eqs. (2)–(4), where Eq. (1) is identically satisfied, we obtain the following ordinary differential equations:



The boundary conditions (5) reduce to

where Pr = ν/α is the Prandtl number and Le = ν/DB is the Lewis number. The constant dimensionless Brownian motion parameter Nb and thermophoresis parameter Nt are defined as

The physical quantities of interest in this study are the local Nusselt number Nux and the local Sherwood number Shx which are defined as

where k is the thermal conductibility of the nanofluid and qw and qm are, respectively, the heat flux and mass flux at the surface (plate), given by

Substituting (6) into (13) and (14), we obtain

where Rex = Uwx/ν is the local Reynolds number.
It is worth mentioning that an anonymous reviewer has pointed out that for the linearly (i.e. n = 1) stretching/shrinking sheet, the exact solution for the flow field is given by

with then bc = λ from the boundary condition f′(0) = λ. Substituting (16) into Eq. (8) for n = 1, gives

and then

so that (18) gives, as it is expected, λc = −S2/4 < 0.
However, for the nonlinearly (i.e. n≠1) stretching case (i.e. λ > 0), there is no exact solution of Eq. (8) (see Vajravelu37 and Cortell38).
Results and discussion
The system of nonlinear ordinary differential equations (8)– (10) with the boundary conditions (11) was solved numerically using a shooting method. The results obtained show the influences of the non-dimensional governing parameters, namely suction parameter S, Lewis number Le, thermophoresis parameter Nt, Brownian motion parameter Nb and stretching/shrinking parameter λ on the velocity profile, temperature profile, nanoparticle concentration profile, the local Nusselt number and the local Sherwood number. Using the present method, dual solutions are found by employing different initial guesses for the missing values of f″(0), −θ′(0) and −ϕ′(0) where all velocity, temperature and nanoparticle concentration profiles satisfy the infinity boundary conditions (11) asymptotically with two different boundary layer thicknesses. To validate the numerical results obtained, the present results for −θ′(0) were compared with those obtained by Rana and Bhargava7 for the case of a stretching surface by setting f(0) = 0 and f′(0) = 1 in the boundary conditions (11) and neglecting the thermophoresis parameter Nt and Brownian motion parameter Nb, i.e. by setting Nt = 0 and Nb = 0. The present results were also compared with those reported by Cortell38 by setting f(0) = 0 and f′(0) = 1 in the boundary conditions (11) and taking Eckert number Ec = 0 in Eq. (15) of that paper. The comparisons as presented in Table 1 show a favorable agreement, thus gives confidence to the results that will be reported for the shrinking case.
The variations of the local Nusselt number  and the local Sherwood number
and the local Sherwood number  with stretching/shrinking parameter λ for S = 2.5,3 and 3.5 are shown in Figs. 1 and 2, respectively. From Figs. 1 and 2, we found that it is possible to obtain dual solutions of the similarity equations (8)– (10) subject to the boundary conditions (11). As shown in Figs. 1 and 2, it is seen that dual solutions exist for the particular suction parameter S = 2.5,3 and 3.5. These findings are supported by the results reported by Fang et al.35 for a permeable shrinking sheet that mentioning the dual solutions occur only with mass suction S ≥ 2. For negative values of λ, there exist a critical value λc with two solutions exist for λ > λc, a unique solution obtained when λ = λc and no solutions exist for λ < λc. Based on our computations, these critical values of λc are −1.4278, −2.0561, −2.7986, −3.6553 and −5.7114 for S = 2.5,3,3.5,4 and 5, respectively. These values are presented in Table 2.
with stretching/shrinking parameter λ for S = 2.5,3 and 3.5 are shown in Figs. 1 and 2, respectively. From Figs. 1 and 2, we found that it is possible to obtain dual solutions of the similarity equations (8)– (10) subject to the boundary conditions (11). As shown in Figs. 1 and 2, it is seen that dual solutions exist for the particular suction parameter S = 2.5,3 and 3.5. These findings are supported by the results reported by Fang et al.35 for a permeable shrinking sheet that mentioning the dual solutions occur only with mass suction S ≥ 2. For negative values of λ, there exist a critical value λc with two solutions exist for λ > λc, a unique solution obtained when λ = λc and no solutions exist for λ < λc. Based on our computations, these critical values of λc are −1.4278, −2.0561, −2.7986, −3.6553 and −5.7114 for S = 2.5,3,3.5,4 and 5, respectively. These values are presented in Table 2.
In the following discussion, we term the first and second solutions in the following discussion by how they appear in Fig. 1, i.e. the first solution has a lower value of  than the second solution for a given λ. For the stretching case (λ > 0), dual solutions are found to exist for all positive values of λ, to much higher values than shown in Figs. 1 and 2. The range λc ≤ λ ≤ 2 was chosen because the solution shows complicated behaviors in this range. For the range λ > 2, these quantities show monotonically increase/decrease behavior. This finding is in accordance with the results reported by Bachok et al.33 that solving the unsteady boundary-layer flow and heat transfer of a nanofluid over a permeable stretching/shrinking sheet. From Fig. 1, it is seen that the values of
than the second solution for a given λ. For the stretching case (λ > 0), dual solutions are found to exist for all positive values of λ, to much higher values than shown in Figs. 1 and 2. The range λc ≤ λ ≤ 2 was chosen because the solution shows complicated behaviors in this range. For the range λ > 2, these quantities show monotonically increase/decrease behavior. This finding is in accordance with the results reported by Bachok et al.33 that solving the unsteady boundary-layer flow and heat transfer of a nanofluid over a permeable stretching/shrinking sheet. From Fig. 1, it is seen that the values of  which represents the heat transfer rate at the surface increases as the suction parameter S increases. This is due to the fact that increasing S is to decrease the thermal boundary layer thickness and in turn increase the temperature gradient at the surface. Fig. 1 also indicates that the critical values |λc| for which the solution exist increase as S increases. This finding suggests that suction widens the region of dual solutions to the similarity equations (8)– (11).
which represents the heat transfer rate at the surface increases as the suction parameter S increases. This is due to the fact that increasing S is to decrease the thermal boundary layer thickness and in turn increase the temperature gradient at the surface. Fig. 1 also indicates that the critical values |λc| for which the solution exist increase as S increases. This finding suggests that suction widens the region of dual solutions to the similarity equations (8)– (11).
The variation of the local Sherwood number  with λ is shown in Fig. 2. It is found that the first solution has a higher value of
with λ is shown in Fig. 2. It is found that the first solution has a higher value of  for a given λ than the second solution. The value of
for a given λ than the second solution. The value of  which represents the wall mass transfer rate increases as S increases as illustrated in Fig. 2. The stability analysis of multiple solutions has been discussed in a number of studies, for example by Weidman et al.40, Paullet and Weidman41, Harris et al.42 and Ro°ca and Pop43. They have shown that the first solution is stable and physically relevant in practice whilst those on the second solutions are not. We expect that this finding holds for the present problem. On the other hand, the values of −θ′(0) and −ϕ′(0) with different values of S for λ = −0.5 and 2 are shown in Table 3.
which represents the wall mass transfer rate increases as S increases as illustrated in Fig. 2. The stability analysis of multiple solutions has been discussed in a number of studies, for example by Weidman et al.40, Paullet and Weidman41, Harris et al.42 and Ro°ca and Pop43. They have shown that the first solution is stable and physically relevant in practice whilst those on the second solutions are not. We expect that this finding holds for the present problem. On the other hand, the values of −θ′(0) and −ϕ′(0) with different values of S for λ = −0.5 and 2 are shown in Table 3.
Fig. 3 shows the variations of the local Nusselt number  with λ for several values of Prandtl number Pr and fixed values of the other parameters. Generally, local Nusselt number increases as Pr increases. From Fig. 3, it is clearly shown that for small values of Pr, i.e. Pr = 0.7 to 1.6, the first solution has a higher value of
with λ for several values of Prandtl number Pr and fixed values of the other parameters. Generally, local Nusselt number increases as Pr increases. From Fig. 3, it is clearly shown that for small values of Pr, i.e. Pr = 0.7 to 1.6, the first solution has a higher value of  for a given λ than the second solution. However, the opposite behaviors are observed for the local Nusselt number for moderate values of Pr, i.e. Pr = 1.8 to 6.2 as presented in Fig. 3. It is noticed that the second solution has a higher value of
for a given λ than the second solution. However, the opposite behaviors are observed for the local Nusselt number for moderate values of Pr, i.e. Pr = 1.8 to 6.2 as presented in Fig. 3. It is noticed that the second solution has a higher value of  compared to the first solution for a given λ.
compared to the first solution for a given λ.
Figs. 4 and 5 have been plotted to demonstrate the effects of suction parameter S on f′(η) representing the velocity profile for both shrinking and stretching cases. For the first solution, it is observed that the velocity increases as S increases for the shrinking case as apparent in Fig. 4. As may be expected, it is because of the fact that suction cause the reduction of momentum boundary layer thickness and consequently enhances the flow near the solid surface. In Fig. 4, we also found that the velocity profiles have positive velocity gradient for the first solution, while the opposite trends are observed for the second solution. In Fig. 5, the fluid velocity inside the boundary layer decreases with an increase in S for the stretching case. This observation occurs due to suction effect which retards the fluid motion as presented in Fig. 5.
Figs. 6 and 7 give the effects of the thermophoresis parameter Nt on the temperature profiles θ(η) while Figs. 8 and 9 are devoted to see the influences of Nt on the nanoparticle concentration profiles ϕ(η). Figs. 6 and 7 elucidate that the temperature profiles as well as the boundary layer thicknesses of the thermal field increase with increasing Nt. As a result, increasing Nt is to decrease the local Nusselt number. Both Figs. 8 and 9 indicate that increasing Nt is to increase the concentration for both first and second solutions and in consequence decrease the nanoparticle concentration gradient at the surface. Hence, the local Sherwood number is expected to decrease as Nt increases. This phenomenon is due to the thermophoresis effect, which warm the fluid in the boundary layer. This finding is in good agreement with that reported in Fig. 6 in the paper by Rana and Bhargava7 for the case of flow and heat transfer over a nonlinearly stretching sheet in a nanofluid without suction effect. It is also found that the positive concentration gradient at the surface ϕ′(0) is obtained for both solutions of Nt = 0.5 and 0.8 while negative concentration gradient at the surface ϕ′(0) is obtained for both solutions of Nt = 0.1 as shown in Figs. 8 and 9, which is consistent with the result presented in Fig. 2.
Figs. 10 and 11 are presented to observe the effect of the Brownian motion parameter Nb on the temperature profiles θ(η) with the corresponding nanoparticle concentration profiles ϕ(η) being shown in Figs. 12 and 13 for both shrinking and stretching cases. These Figs. 10 and 11 indicate that by increasing the Brownian motion parameter Nb, the temperature and the thermal boundary layer thickness increase. This phenomenon leads to decrease the local Nusselt number. Different nanoparticles have different values of Nb and Nt. This leads to different heat transfer rate. These two parameters can be used to control the heat transfer rate in a nanofluid. Also, we can see that in Figs. 10 and 11, the usual decay occurs to the temperature profiles for all values of Nb considered and the thermal boundary layer thickness increases rapidly for large values of Nb. It is observed that the effect of Nb on the nanoparticle concentration profile ϕ(η) is in the opposite manner to that of temperature profiles θ(η) as illustrated in Figs. 12 and 13. It is apparent from Figs. 12 and 13 that nanoparticle concentration is decreasing as Nb increasing. It seems that the Brownian motion acts to warm the fluid in the boundary layer and at the same time exacerbates particle deposition away from the fluid regime to the surface which resulting in a decrease of the nanoparticle concentration boundary layer thickness for both solutions. As a consequence, the concentration gradient at the surface increases and in turn increases the local Sherwood number. This finding is in accordance with the result reported in Fig. 4 by Rana and Bhargava7. The thermal conduction can be enhanced in two ways by the Brownian motion of nanoparticles. First, it can be enhanced by a direct effect owing to nanoparticles that transport heat and the second mechanism is by an indirect micro-convection of fluid surrounding individual nanoparticles. The high values of Nb means Brownian motion is strong for the small particle and the opposite case is applied for small values of Nb (Rana and Bhargava7). Thus, from Figs. 10,11,12,13, it is clearly indicated that Brownian motion parameter provides important effect on temperature and concentration.
Figs. 14 and 15 are depicted to examine the effects of the Lewis number Le on the temperature profiles θ(η) while the corresponding nanoparticle concentration profiles ϕ(η) are presented in Figs. 16 and 17 for both shrinking and stretching cases, respectively. It is seen from Figs. 14 and 15, the temperature increases as the parameter Le is increased, resulting in an increasing manner of the thermal boundary layer thickness, which consequently reduces the local Nusselt number. However, the nanoparticle concentration profile acts in the opposite behavior with the increasing of Le for both solutions as shown in Figs. 16 and 17. It is found that the concentration of both solutions decrease as Le increases. There would be a significant reduction in the concentration boundary layer thickness for both first and second solutions when Le is increased. This phenomenon occurs due to Lewis number effects which increases the concentration gradient at the surface and as a result increases the local Sherwood number. It is also seen that the boundary layer thicknesses of nanoparticle concentration for the second solutions for some values of Le are larger than the first solutions in both stretching and shrinking cases, which support the instability of the second solutions. The positive concentration gradient at the surface ϕ′(0) is obtained for both solutions for small values of Le i.e. Le = 1 and 2 as depicted in Figs. 16 and 17. The opposite trends are displayed in the direction of the concentration gradient at the surface when large values of Le are applied for example Le = 5 as shown in Figs. 16 and 17. It is worth mentioning that in all Figs. 4,5,6,7,8,9,10,11,12,13,14,15,16,17 presented here, the velocity, temperature and nanoparticle concentration profiles satisfy the far field boundary conditions (11) asymptotically, which support the validity of the numerical results obtained.
Conclusions
This paper presents a similarity solution of the boundary layer flow and heat transfer over a nonlinearly stretching/shrinking sheet immersed in a nanofluid with suction effect. By means of similarity transformation, the governing mathematical equations are reduced into ordinary differential equations which are then solved numerically using a shooting method. The effects of some governing parameters namely suction parameter, thermophoresis parameter, Brownian motion parameter and stretching/shrinking parameter on the flow, concentration and heat transfer characteristics are graphically presented and discussed. The findings of the numerical results can be summarized as follows:
-
1
The local Nusselt number and the local Sherwood number which respectively represent the heat transfer and mass transfer rates increase with an increase in the suction parameter.
-
2
The increasing of thermophoresis parameter Nt and the Brownian motion parameter Nb is to increase the temperature in the boundary layer which consequently reduces the heat transfer rate at the surface.
-
3
A rising value in Nb and the decreasing in Nt produce a decrease in the nanoparticle concentration, as a result increases the local Sherwood number.
-
4
The increase of Lewis number Le leads to an increase of the temperature but a decrease in the nanoparticle concentration.
-
5
Dual solutions exist for a certain range of the stretching/shrinking parameter λ for both shrinking and stretching cases. For the shrinking case, the solution exists up to the critical values of λc(<0), while for the stretching case, the solution could be obtained for all positive values of λ.
-
6
The critical value |λc| increases as the suction parameter S increases, suggest that suction widens the range of λ for which the solution exists.
References
Kumaran, V., Banerjee, A. K., Vanav Kumar, A. & Vajravelu, K. MHD flow past a stretching permeable sheet. Appl. Math. Comp. 210, 26–32 (2009).
Hayat, T., Javed, T. & Abbas, Z. Slip flow and heat transfer of a second grade fluid past a stretching sheet through a porous space. Int. J. Heat Mass Transfer 51, 4528–4534 (2008).
Ishak, A., Nazar, R. & Pop, I. Heat transfer over an unsteady stretching permeable surface with prescribed wall temperature. Nonlinear Anal. RWA 10, 2909–2913 (2009).
Mahapatra, T. R., Nandy, S. K. & Gupta, A. S. Magnetohydrodynamic stagnation-point flow of a power-law fluid towards a stretching surface. Int. J. Non-Linear Mech. 44, 124–129 (2009).
Fang, T., Zhang, J. & Yao, S. A new family of unsteady boundary layers over a stretching surface. Appl. Math. Comp. 217, 3747–3755 (2010).
Makinde, O. D. & Aziz, A. Boundary layer flow of a nano fluid past a stretching sheet with a convective boundary condition. Int. J. Therm. Sci. 50, 1326–1332 (2011).
Rana, P. & Bhargava, R. Flow and heat transfer of a nanofluid over a nonlinearly stretching sheet: A numerical study. Commun. Nonlinear Sci. Numer. Simulat. 17, 212–226 (2012).
Mahmoud, M. A. A. & Megahed, A. M. Non-uniform heat generation effect on heat transfer of a non-Newtonian power-law fluid over a non-linearly stretching sheet. Meccanica 47, 1131–1139 (2012).
Rahman, M. M. & Eltayeb, I. A. Radiative heat transfer in a hydromagnetic nanofluid past a non-linear stretching surface with convective boundary condition. Meccanica 48, 601–615 (2013).
Khan, M. & Shahzad, A. On stagnation point flow of Sisko fluid over a stretching sheet. Meccanica 48, 2391–2400 (2013).
Mukhopadhyay, S. Effects of thermal radiation and variable fluid viscosity on stagnation point flow past a porous stretching sheet. Meccanica 48, 1717–1730 (2013).
Khan, W. A. & Pop, I. Boundary-layer flow of a nanofluid past a stretching sheet. Int. J. Heat Mass Transfer 53, 2477–2483 (2010).
Daungthongsuk, W. & Wongwises, S. A critical review of convective heat transfer nanofluids. Renew. Sust. Energ. Rev. 11, 797–817 (2007).
Choi, S. U. S. Enhancing thermal conductivity of fluids with nanoparticles in Developments and Applications of Non-Newtonian Flows, Singer, D. A. & Wang, H. P. Eds., vol. 231, pp. 99–105, American Society of Mechanical Engineers, New York (1995).
Das, S. K., Choi, S. U. S., Yu, W. & Pradeep, T. Nanofluids: science and technology (Wiley, New Jersey, 2007).
Kakaç, S. & Pramuanjaroenkij, A. Review of convective heat transfer enhancement with nanofluids. Int. J. Heat Mass Transfer 52, 3187–3196 (2009).
Wong, K. V. & De Leon, O. Applications of nanofluids: current and future. Adv. Mech. Eng. 2010, Article ID 519659, 1–11 (2010).
Saidur, R., Leong, K. Y. & Mohammad, H. A. A review on applications and challenges of nanofluids. Renew. Sust. Ener. Rev. 15, 1646–1668 (2011).
Fan, J. & Wang, L. Review of heat conduction in nanofluids. ASME J. Heat Transfer 133, Article ID 040801, 1–14 (2011).
Jaluria, Y., Manca, O., Poulikakos, D., Vafai, K. & Wang, L. Heat transfer in nanofluids. Adv. Mech. Eng. 2012, Article ID 972973, 1–2 (2012).
Mahian, O., Kianifar, A., Kalogirou, S. A., Pop, I. & Wongwises, S. A review of the applications of nanofluids in solar energy. Int. J. Heat Mass Transfer 57, 582–594 (2013).
Miklavčič, M. & Wang, C. Y. Viscous flow due to a shrinking sheet. Quart. Appl. Math. 64, 283–290 (2006).
Wang, C. Y. Stagnation flow towards a shrinking sheet. Int. J. Non-Linear Mech. 4, 377–382 (2008).
Hayat, T., Abbas, Z. & Sajid, M. On the analytic solution of magnetohydrodynamic flow of a second grade fluid over a shrinking sheet. ASME J. Appl. Mech. 74, 1165–1171 (2007).
Sajid, M., Hayat, T. & Javed, T. MHD rotating flow of a viscous fluid over a shrinking surface. Nonlinear Dyn. 51, 259–265 (2008).
Bachok, N., Ishak, A. & Pop, I. Stagnation-point flow over a stretching/shrinking sheet in a nanofluid. Nanoscale Res. Lett. 6, Article ID 623, 1–10 (2011).
Bachok, N., Ishak, A. & Pop, I. Boundary layer stagnation-point flow and heat transfer over an exponentially stretching/shrinking sheet in a nanofluid. Int. J. Heat Mass Transfer 55, 8122–8128 (2012).
Zaimi, K., Ishak, A. & Pop, I. Boundary layer flow and heat transfer past a permeable shrinking sheet in a nanofluid with radiation effect. Adv. Mech. Eng. 2012, Article ID 340354, 1–7 (2012).
Ishak, A., Lok, Y. Y. & Pop, I. Stagnation-point flow over a shrinking sheet in a micropolar fluid. Chem. Eng. Comm. 197, 1417–1427 (2010).
Bhattacharyya, K. Boundary layer flow and heat transfer over an exponentially shrinking sheet. Chin. Phys. Lett. 28, Article ID 074701, 1–4 (2011).
Bhattacharyya, K. Dual solutions in unsteady stagnation-point flow over a shrinking sheet. Chin. Phys. Lett. 28, Article ID 084702, 1–4 (2011).
Bhattacharyya, K., Mukhopadhyay, S., Layek, G. C. & Pop, I. Effects of thermal radiation on micropolar fluid flow and heat transfer over a porous shrinking sheet. Int. J. Heat Mass Transfer 55, 2945–2952 (2012).
Bachok, N., Ishak, A. & Pop, I. Unsteady boundary-layer flow and heat transfer of a nanofluid over a permeable stretching/shrinking sheet. Int. J. Heat Mass Transfer 55, 2102–2109 (2012).
Rohni, A. M., Ahmad, S. & Pop, I. Flow and heat transfer over an unsteady shrinking sheet with suction in nanofluids. Int. J. Heat Mass Transfer 55, 1888–1895 (2012).
Fang, T., Zhang, J. & Yao, S. Viscous flow over an unsteady shrinking sheet with mass transfer. Chin. Phys. Lett. 26, Article ID 014703 (2009).
Zheng, L., Wang, L. & Zhang, X. Analytic solutions of unsteady boundary flow and heat transfer on a permeable stretching sheet with non-uniform heat source/sink. Commun. Nonlinear Sci. Numer. Simulat. 16, 731–740 (2011).
Vajravelu, K. Viscous flow over a nonlinearly stretching sheet. Appl. Math. Comput. 124, 281–288 (2001).
Cortell, R. Viscous flow and heat transfer over a nonlinearly stretching sheet. Appl. Math. Comput. 184, 864–873 (2007).
Buongiorno, J. Convective transport in nanofluids. ASME J. Heat Transfer 128, 240–250 (2006).
Weidman, P. D., Kubitschek, D. G. & Davis, A. M. J. The effect of transpiration on self-similar boundary layer flow over moving surfaces. Int. J. Eng. Sci. 44, 730–737 (2006).
Paullet, J. & Weidman, P. Analysis of stagnation point flow toward a stretching sheet. Int. J. Nonlinear Mech. 42, 1084–1091 (2007).
Harris, S. D., Ingham, D. B. & Pop, I. Mixed convection boundary layer flow near the stagnation point on a vertical surface in a porous medium: Brinkman model with slip. Trans. Porous Media 77, 267–285 (2009).
Roşca, A. V. & Pop, I. Flow and heat transfer over a vertical permeable stretching/shrinking sheet with a second order slip. Int. J. Heat Mass Transfer 60, 355–364 (2013).
Acknowledgements
The financial supports received from the Ministry of Higher Education, Malaysia (Project Code: FRGS/1/2012/SG04/UKM/01/1) and the Universiti Kebangsaan Malaysia (Project Code: DIP-2012-31) are gratefully acknowledged.
Author information
Authors and Affiliations
Contributions
K.Z. and A.I. performed the numerical analysis and wrote the manuscript. I.P. carried out the literature review and co-wrote the manuscript.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Rights and permissions
This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivs 3.0 Unported License. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-nd/3.0/
About this article
Cite this article
Zaimi, K., Ishak, A. & Pop, I. Boundary layer flow and heat transfer over a nonlinearly permeable stretching/shrinking sheet in a nanofluid. Sci Rep 4, 4404 (2014). https://doi.org/10.1038/srep04404
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep04404
This article is cited by
-
Variation of the shape of Fe3O4-nanoparticles on the heat transfer phenomenon with the inclusion of thermal radiation
Journal of Thermal Analysis and Calorimetry (2022)
-
Rotational nanofluids for oxytactic microorganisms with convective boundary conditions using bivariate spectral quasi-linearization method
Journal of Central South University (2020)
-
Aligned magnetic field and Navier slip effects on free convective radiative flow of nanofluids with imbedded carbon nanotubes: a Lie group analysis
SN Applied Sciences (2020)
-
Effects of radiation on mixed convection stagnation-point flow of MHD third-grade nanofluid over a vertical stretching sheet
Journal of Thermal Analysis and Calorimetry (2019)
-
Enhancement in heat and mass transfer over a permeable sheet with Newtonian heating effects on nanofluid: Multiple solutions using spectral method and stability analysis
Pramana (2019)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.



 with λ for various values of S when n = 2, Le = 2, Nt = 0.5, Nb = 0.5 and Pr = 6.2.
with λ for various values of S when n = 2, Le = 2, Nt = 0.5, Nb = 0.5 and Pr = 6.2.
 with λ for various values of S when n = 2, Le = 2, Nt = 0.5, Nb = 0.5 and Pr = 6.2.
with λ for various values of S when n = 2, Le = 2, Nt = 0.5, Nb = 0.5 and Pr = 6.2.
 with λ for various values of Pr when n = 2, Le = 2, Nt = 0.5, Nb = 0.5 and S = 2.5.
with λ for various values of Pr when n = 2, Le = 2, Nt = 0.5, Nb = 0.5 and S = 2.5.












