The concept of synchronized behavior in coupled systems is pervasive in both nature1 and physical systems2. Examples of synchronization include rhythmic blinking of fireflies3, rhythmic hands clapping after a musical performance4, crowd synchrony on the oscillating bridge5,6 and the spin-orbit resonance of the planet Mercury7. In physical systems, synchronization has been studied for more than three centuries, starting with Huygens' experiment with two coupled pendulum clocks8,9 and leading to modern-day experiments of coupled nano-oscillators10,11,12 and chaos based communication13,14. These examples illustrate fundamental elements of synchronization: the individual units display periodic motion, they display adjustable phase and frequency and they couple15.

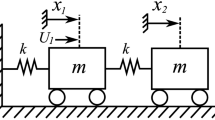
Consider the system of n globally coupled excited identical units as shown in Figure 1(a,b) (example for n = 6). For the appropriately chosen coupling such a system can reach the state of complete synchronization2,15 (all the units behave identically). However, in such a system it is possible that some units suddenly (breakdown of energy supply) or gradually (as the effect of aging and fatigue) loss their excitation. Here, we show that in such case the synchronization can extend the life time of the desirable behavior of the coupled system. As proof of concept, we examine the mechanical implementation of globally coupled system, i.e., the system of n rotating pendula mounted to the beam which can move in horizontal direction as shown in Figure 1(a,b) (example for 6 pendula) and assume that the rotation of all pendula is a desired behavior of coupled system. Initially all pendula are excited and reach complete synchronization as shown in Figure 1(a), them the excitation of some pendula is swiched off. We show that all pendula can still rotate but the unexcited pendula (two green pendula in Figure 1(b)) are phase shifted with the excited pendula (three red pendula in Figure 1(b)).

Figure 1
figure 1

System of 6 globally coupled units and its mechanical implementation as a system of 6 externally forced pendula mounted to the beam which can move horizontally, (a) all units (pendula) are externally excited (red color) and synchronized, (b) two units (green color are not excited – the cluster of four excited pendula is phase synchronized with the cluster of two unexcited pendula.

Full size image

The selection of this example has been motivated by the studies of Blekhman16 who considers the case of two identical (or nearly identical) unbalanced rotors mounted on the oscillating base. It has been shown the oscillations of the base can maintain the rotation of one rotor when its excitation is switched off (effect of the oscillatory maintenance of rotation which is also used in the well-known game ‘hoola-hoop’). Contrary to these studies we are not assuming weak coupling between pendula and not using small parameter method which for example do not allow identification of co-existing synchronous states17,18. Our considerations of two synchronized pendula with significantly different masses allow generalization of our results to the case on n pendula.

In our studies we consider the system shown in Figure 2(a). It consists of a rigid beam of mass mB on which n rotating pendula are mounted. In Figure 3(a,b) the beam is connected to a stationary base by the spring (or springs) with stiffness coefficient kx and a damper (or dampers) with a damping coefficient cx. Due to the existence of the forces of inertia, which act on each pendulum pivot, the beam can move in horizontal directions (this motion is described by coordinate x). The masses of the pendula are indicated as mi; li are the lengths of the pendula. The rotation of the i-th pendula is described by φi. The rotations of the pendula are damped by linear dampers with damping coefficient cφi. Each pendulum is driven by the drive torque inversely proportional to its velocity: . If any other external forces do not act on the pendulum, then under the action of such a torque it rotates with constant angular velocity . As the system is in a gravitational field (g = 9.81[m/s2] − acceleration of gravity), the weight of the pendulum causes the unevenness of its rotation: the pendulum slows down, when the center of mass rises up and accelerates when the center of mass falls down. The effect of gravity is important in the case of slow rotations of the pendula16,17,18. To explain how the synchronization can be achieved in the systems of Figure 2(a) first consider the case of identical pendula and nonmovable beam. In this case all pendula have the same period of rotations (the pendula have the same masses and lengths). The rotations of the pendula are initiated by non-zero initial conditions and the pendula's evolutions tend to the limit cycles. The pendula are not coupled and the phase angles between their displacements have fixed values, depending on initial conditions. Any perturbation of the pendula results in the changes of these angles. When the beam can move, its oscillations excited by the forces with which pendula act on it, cause the changes of the phase shifts between the pendula's displacements and differentiate the angular velocity of their rotations. When after the transient time, all pendula have the same angular velocity of rotation and there are constant phase shifts between the pendula's displacements, we can say that the pendula achieve synchronization. The state of synchronization is achieved when the motion of the system is periodic and there are constant phase shifts between the pendula displacements16,17,18. The values of the phase shifts characterize the synchronous configuration and are independent of the initial conditions.

Figure 2
figure 2

(a) n externally forced pendula mounted to the beam which can move horizontally; (b,c) The regions of the parameters kx − mb space of complete C (green), antiphase A (navy blue), quasiperiodic Q (violet) synchronizations for the system of two pendula with different masses rotating in the same direction; N indicated the region in which pendulum 2 stops, l = 0.25[m], cφ = 0.03[Nsm], p01 = p02 = 5.0[Nm], p11 = p12 = 0.2[Nms], (b) m1 = 1.9[kg] and m2 = 0.1[kg], after the initial time equal to 50N, excitation of pendulum 2 is switched off, (c) m1 = 0.9[kg] and m2 = 1.1[kg], after the initial time equal to 50N, excitation of pendulum 2 is switched off.

Full size image
Figure 3
figure 3

(a,b,e,f,g,h) Time series showing the transient behavior of pendula's angular velocities , the difference of pendula's displacement φj − φi (i ≠ j) and beam's displacement x (magnified 100 times) in the case when the excitations of a number of pendula are switched off: p01 = 5.0, p11 = 0.2, p02 = 5.0, p12 = 0.2, p21 = p22 = 0, kx = 7000.0[N/m], mb = 12.0[kg], (a) n = 2, m1 = 1.9[kg], m2 = 0.1[kg], the excitation of pendulum 2 switched off at N = 20, (b) m1 = 0.85[kg], m2 = 1.15[kg]) the excitation of pendulum 2 switched off at 50N. (c,d) Bifurcation diagrams of pendula's angular velocities and the difference of pendula's displacement φ2 − φ1 versus parameter ξ, excitation of pendulum 2 gradually decays to zero, i.e., , n = 2, m1 = 1.9[kg], m2 = 0.1[kg] (c) kx = 7000.0[N/m], mb = 12.0[kg], (d) kx = 3700.0[N/m], mb = 18.0[kg], (e–h) n = 20, identical pendula with mass m1–20 = 0.1, (e,f) at N = 50, excitation of p pendula is simultaneously switched off, (e) p = 11, (f) p = 12, (g,h) n = 20 identical pendula, m1–20 = 0.1[kg], at the moments indicated by the arrows the excitations of one pendulum is switched off, (g) excitation of 11 pendula is switched off at N = 50, 60,…150, excitation of the 12-th pendulum is switched off at N = 300, (h) excitation of 12 pendula are switched off for N = 50,60,…150,160, excitation of the 13-th pendulum is switched off for N = 220.

Full size image

First let us consider the case of two pendula with different masses (m1≠m2). Figure 2(b,c) shows the dependence of the synchronous configuration on the parameters kx and mb. After the initial time N = 50 during which the pendula reach complete (phase shift between pendula is equal to zero), antiphase (phase shift between pendula is equal to π) or quasiperiodic (pendula perform identical quasiperiodic rotation) synchronizations the excitation of pendulum 2 is switched off. Figure 2(b) illustrates the case of m1 = 1.9[kg] and m2 = 0.1[kg]. In regions indicated in green, navy blue and violet colors the pendula are respectively in the state of complete C, antiphase A, quasiperiodic Q synchronizations when the excitation of pendulum 2 is switched off. In region N pendulum 2 stops. The synchronization and the rotation of both pendula are preserved but the complete synchronization is replaced by phase synchronization (phase shift not equal to zero or π). For the wide range of kx and mb parameters the desired behavior of the coupled system is preserved. Contrary to this for m1 = 0.9[kg] and m2 = 1.1[kg] the set parameters for which both pendula rotate is very small as shown in Figure 2(c). Notice that in this case the excitation of the heavier pendulum has been switched off.

Figure 3(a,b) shows time series of the transient behavior of pendula's angular velocities , the difference of pendula's displacement φ2 − φ1 and beam's displacement x (magnified 100 times) in the case when the excitation of pendulum 2 is switched off (m1 = 1.9[kg], m2 = 0.1[k] and mb = 12.0[kg], kx = 7000[N/m]). Both pendula are in the state of complete synchronization when at time 20N the excitation of pendulum 2 is switched off. After the transient time the system reaches the state of phase synchronization with nonzero phase shift between pendula. Both pendula rotate with the same angular velocity (smaller that before the switch off). Figure 3(b) shows the case for m1 = 0.85[kg] and m2 = 1.15[kg]. At time 20N the excitation of pendulum 2 is switched off. Synchronization and rotation of both pendula are preserved but the phase shift φ2 − φ1 increases to the value larger than π/2. Further increase of the difference of pendula's masses (down to m1 = 0.83[kg] and m2 = 1.17[kg]) leads to the loss of synchronization and pendulum 2 stops.

Now let us consider the case when the excitation of pendulum 2 gradually decays to zero. The excitation decay can be described as , where ξ (ξ ∈ [0,1]) is a control parameter. The bifurcation diagrams shown in Figure 3(c,d) present the values of the pendula's angular velocities (at the moments when pendulum 1 moves through the lower equilibrium position) and the difference of pendula's displacement φ2 − φ1 versus parameter ξ. In the case of Figure 3(c) (kx = 7000.0[N/m], mb = 12.0[kg], both pendula are initially in the state of complete synchronization) synchronization is preserved up to the value ξ = 0.85. The phase shift between pendula is visible for larger values of ξ (complete synchronization is replaced by phase synchronization). In the whole interval of ξ pendulum 1 transfers enough energy to pendulum 2 to ensure the pendula's synchronization. The difference of the pendula's displacements φ2 − φ1 is so small that it is not visible (in the scale of Figure 3(c)). The case of kx = 3700[N/m] and mb = 18[kg] is illustrated in Figure 3(d). In the interval 0.0 < ξ < 0.49 one observes periodic rotations of the synchronized pendula (with the phase shift larger than zero). For larger values of ξ (0.49 < ξ < 0.70) pendula perform periodic synchronous rotations with higher periods or quasiperiodic synchronous rotations. Further increase of ξ < 0.70 stops pendulum 2.

In the state of complete synchronization the forces with which pendula act on the beam are algebraically added9,16,17,18 so this example can be generalized to the case of any number of pendula of total mass equal to m1+ m2. Consider the case of n pendula in the state of complete synchronization. The effect of the switch off of the excitation of p pendula is the same as the effect of switch off of the excitation of pendulum with mass (m1+ m2)p/n in the system of two pendula (the second one with mass (m1+ m2)(n − p)/n). As an example consider the system of 20 identical pendula rotating in the same direction with masses (m1–20 = 0.1[kg], mb = 12.0[kg], kx = 7000[N/m] shown in Figure 3(e–f). All pendula are in the state of complete synchronization when at time 50N the excitation of eleven (Figure 3(e)) and twelve (Figure 3(f)) pendula is switched off. Up to the case of 11 pendula the initial complete synchronization is replaced by the phase synchronization and all pendula rotate. The phase shift between the clusters of excited and unexcited pendula increases with the increase of the number of unexcited pendula. When the excitation of the 12 pendula is switched off the synchronization is lost and all unexcited pendula stop to rotate as shown in Figure 3(f).

In the considered examples a number of pendula losses excitation simultaneously, if the pendula's excitation is switched off one by one scenario can be different. In the case described in Figure 3(g,h) (m1–20 = 0.1[kg], mb = 12.0[kg], kx = 7000[N/m]) the excitation is switched off at the moments indicated by arrows. In Figure 3(g) eleven pendula are losing excitations in the time intervals of 10N starting at 50N. The increase of the phase shift between the clusters of excited and unexcited pendula is visible. For N = 300 the excitation of the 12-th pendulum is switched off leading to the loss of synchronization (12 pendula stop to rotate). Different scenario is described in Figure 3(h). The 12-th pendulum loses excitation just after 11-th at N = 160. Shortly after it 11 pendula (which lost excitation before) stop to rotate but the 12-th pendulum still rotates and is phase synchronized with the cluster of 8 excited pendula (the phase shift is close to π/4). Later at N = 220 the 13-th pendulum loses excitation and two clusters of 7 excited and 2 unexcited are created.

Our examples show that it is possible to estimate the critical number of pendula which excitation can be switched off and the rotation of all of them is preserved. In the case when the pendula's excitations are switched off non-simultaneously it is possible to observe the case in which unexcited pendula form two groups one of them stops to rotate and the second one rotates and is phase synchronized with the excited pendula.

The described phenomenon has been observed experimentally - Figure 4(a,b). A simple rig consisting of three direct-current electrical motors mounted on the wooden plate which can oscillate horizontally (details on the experimental rig are provided in the Supplementary Information) has been considered. The pendula are mounted at the end of the motor's rods. The control system has been used to vary the angular velocity of pendula's rotation. Figure 4(a) shows the case when all pendula are excited and reach the state of complete synchronization. Next the excitation of the left pendulum has been switched off. Both pendula still rotate (slower than in the previous case) and there is a phase shift between excited pendula and unexcited pendulum as - Figure 4(b).

Figure 4
figure 4

Experimental observation, (a) synchronous rotation of 3 excited pendula, (b) phase synchronization between two excited pendula (left and middle) and unexcited pendulum (right).

Full size image

Thus we have shown that the initial synchronization extends the life-time of the desired behavior of the coupled system. It is possible to estimate the critical number of units which excitation can be switched off and the behavior of the system is not changed qualitatively. The appearance of the phase shift between some units, i.e., transition from the complete to the phase synchronization can be considered as the indicator of the breakdown of excitation in some units. We expect the physical mechanisms that we uncovered here will have important and far-reaching ramifications in the design and use of engineering devices base on coupled systems and in understanding of coupled systems' behavior in nature.

Methods are available in the Supplementary Information.