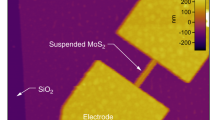
Abstract
Mechanical exfoliation is a convenient and effective approach to deriving two-dimensional (2D) nanodevices from layered materials; but it is also generally perceived as unpreferred as it often yields devices with structural irregularities and nonidealities. Here we show that such nonidealities can lead to new and engineerable features that should be embraced and exploited. We measure and analyze high frequency nanomechanical resonators based on exfoliated 2D molybdenum disulfide (MoS2) structures and focus on investigating the effects of structural nonidealities and asymmetries on device characteristics and performance. In high and very high frequency (HF/VHF) vibrating MoS2 devices based on diaphragms of ~2−5 μm in size, structural nonidealities in shape, boundary and geometric symmetry all appear not to compromise device performance, but lead to robust devices exhibiting new multimode resonances with characteristics that are inaccessible in their ‘ideal’ counterparts. These results reveal that the seemingly irregular and nonideal 2D structures can be exploited and engineered for new designs and functions.
Similar content being viewed by others
Introduction
Two-dimensional (2D) nanostructures in graphene and transition metal dichalcogenides (TMDCs), derived from their corresponding layered materials in bulk, have recently attracted significant attention due to their unique properties for creating new devices with potential for nanoelectronics, optoelectronics and transducers1,2,3,4. In device fabrication, it was mechanical exfoliation that helped make a breakthrough in isolating atomically thin 2D devices from layered materials, yielding graphene from graphite5. The seemingly simple mechanical exfoliation method comes along with great intuition and insight – it takes advantage of the fact that atomic sheets/planes are weakly bonded by van der Waals interactions in layered materials such as graphite and TMDCs. In practice, its convenience, cleanness (especially in the device region) and low cost (e.g., via Scotch tapes) add to its merits. Following graphene, atomically thin hexagonal boron nitride (h-BN), molybdenum disulfide (MoS2) and other TMDCs have been successfully obtained using exfoliation, in realizing the first 2D devices from these crystals6. Today, ‘handcraft’ of mechanical exfoliation is still an important and effective approach to yielding pristine and high-quality 2D nanodevices, including sophisticated heterostructures7,8,9,10,11. While exfoliation can be limited by hand operations in practice (perhaps primarily on being at small scale) today, there is great room in advancing scalable exfoliation-type machineryprocesses to systematically and fully exploit the weak van der Waals interactions in crystals of layered materials.
In current prevailing 2D nanostructures and devices made by exfoliation methods, structural nonidealities in shape, boundary and geometric asymmetry are known to exist. These nonidealities have hitherto usually been deemed undesirable; and such nonideal-looking structures are generally discarded. There has been no systematic study on how the nonideal appearances and geometric irregularities actually affect these structures as devices.
In this work, we use nanomechanical resonators made of ultrathin suspended MoS2 layers as prototypical 2D devices and systematically investigate the effects of structural nonidealities on their attributes and performance. We choose MoS2 because it is a 2D semiconductor (different than graphene) with band structure depending on number of layers (thickness) and tunable via strain12,13,14. Lately it is also suggested that MoS2 resonators may be intrinsically less dissipative than graphene counterparts owing to reduced phonon-phonon damping15. The nonidealities we focus on include irregular shapes/edges and asymmetric geometries. From extensive measurements and modeling, we demonstrate that “nonideal” MoS2 structures can actually make robust and uniquely interesting multimode nanomechanical resonators, offering new opportunities for both fundamental studies and novel technological applications; we also explain the observed effects and develop guidelines for engineering such devices toward potential utilization.
Suspended MoS2 flakes are made by mechanical exfoliation of MoS2 onto prefabricated microtrenches, to produce MoS2 nanomechanical resonators with a diaphragm-on-microtrench drumhead structure (see Methods and Supplementary Information S1). Devices with different types of geometrical nonidealities can be obtained. To directly measure these pristine exfoliated structures and avoid possible contaminations in any extra processing steps (e.g., coating with polymer, patterning contact electrodes), here we employ laser interferometric techniques that were often used for nanomechanical resonators in conventional materials16,17,18,19,20; and we have further carefully engineered the interferometric readout techniques (with significant improvement in displacement sensitivity) so that we are able to directly observe the undriven (no external drive), intrinsic thermomechanical (Brownian) motions of our nanoscale 2D structures21,22 (see Methods and Supplementary Information S2 for details).
Results and discussion
Incomplete drumhead devices with free edges
We first investigate the effects due to the nonideality of incomplete MoS2 coverage over the microtrenches. When a microtrench is not completely covered, we have a partial drumhead structure (Fig. 1a and b) whose perimeter is partly unclamped, exhibiting an open arc and a free edge (a chord corresponding to the open arc). As illustrated in the SEM images, θ is the central angle of the open arc. We call θ the “open angle”, which measures the degree of incomplete coverage of the microtrench. Despite its geometry of being an incomplete drumhead, such structures still make robust nanomechanical resonators. The resonances are found to fit well to the damped harmonic resonator model,  (see Supplementary Information S3 for details), with quality (Q) factors comparable to Q values of the devices based on their ideal, completely-covered counterparts (see Supplementary Information S4 & Supplementary Table S1 for details of multiple devices).
(see Supplementary Information S3 for details), with quality (Q) factors comparable to Q values of the devices based on their ideal, completely-covered counterparts (see Supplementary Information S4 & Supplementary Table S1 for details of multiple devices).
Characteristics and features of nanomechanical MoS2 resonators with incomplete drumhead geometries.
(a): SEM image (top), optical image (bottom) and measured mechanical resonance of a device with diameter d = 2.53 μm, thickness t = 43.1 ± 1.4 nm and open angle θ ≈ 100°. (b): Images and measured data from another device with d = 2.69 μm, t = 62.2 ± 0.7 nm and θ ≈ 102°. Scale bars (for SEM images only): 2 μm. (c): The computed fversus θ curves (θ resolution: 2°) and mode shapes of the three lowest modes for a device with d = 6 μm and t = 30.3 nm (dimensions based on device #4 in Supplementary Information Table S1). The computed mode shapes are shown for selected θ values (integer multiples of 30°, indicated by the open squares on the curves). (d): Comparison of the f−θ curves between a small/thick device (solid curves, d = 1 μm, t = 100 nm, left y axis) and a large/thin device (dashed curves, d = 10 μm, t = 10 nm, right y axis). (e): Dependence of the clamping length (∝keff), resonator area (∝Meff) and resulting frequency f ∝ (keff/Meff)½ on the open angle θ (all values normalized to the θ = 0 case, i.e., the fully clamped case).
We analyze the effects of incomplete drumhead structure by using finite element modeling (FEM, in COMSOL). Figure 1c shows the computed resonance frequencies and mode shapes for the 3 lowest flexural modes fi (f1 → , f2a →
, f2a → , f2b →
, f2b → ), as functions of the open angle θ, for a partially clamped device (with diameter d = 6 μm and thickness t = 30.3 nm). Note here f1 is the fundamental mode with no nodal line in the mode shape, f2a is the mode with a single nodal line in parallel to the free edge and f2b is the mode with a single nodal line perpendicular to the free edge, respectively. A few interesting features are observed. First, the resonance frequency is not a monotonic function of open angle: as θ increases, fi(θ) first decreases, then increases. All the 3 lowest modes exhibit this pattern. Second, the shapes of the fi(θ) curves, such as the open angle θm at which the frequency assumes its minimum fi,m = fi(θm), depends on the individual mode (with index i). This leads to mode crossing (f2a values surpassing f2b value) at θ ~ 137°. Third, the shape of each curve does not show strong dependence on the device dimensions. Shown in Fig. 1d for a larger thin device (d = 10 μm, t = 10 nm) and a smaller thick device (d = 1 μm, t = 100 nm), the solid and dashed curves overlap each other (after rescaling), despite the 100 times difference in aspect ratio d/t (diameter/thickness). These observations on the fi(θ) curves open a new possibility of mode shape engineering by designing and tuning the open angle θ of an incompletely clamped diaphragm. As demonstrated in Fig. 1c, for fully covered devices (θ = 0 only), one is limited in the frequency ratios between the modes and in degenerate mode pairs with small and random frequency splitting. With θ ≠ 0, one can adjust the θ value and choose many possible frequency ratios between different modes and the mode sequence can also be changed by engineering the θ values.
), as functions of the open angle θ, for a partially clamped device (with diameter d = 6 μm and thickness t = 30.3 nm). Note here f1 is the fundamental mode with no nodal line in the mode shape, f2a is the mode with a single nodal line in parallel to the free edge and f2b is the mode with a single nodal line perpendicular to the free edge, respectively. A few interesting features are observed. First, the resonance frequency is not a monotonic function of open angle: as θ increases, fi(θ) first decreases, then increases. All the 3 lowest modes exhibit this pattern. Second, the shapes of the fi(θ) curves, such as the open angle θm at which the frequency assumes its minimum fi,m = fi(θm), depends on the individual mode (with index i). This leads to mode crossing (f2a values surpassing f2b value) at θ ~ 137°. Third, the shape of each curve does not show strong dependence on the device dimensions. Shown in Fig. 1d for a larger thin device (d = 10 μm, t = 10 nm) and a smaller thick device (d = 1 μm, t = 100 nm), the solid and dashed curves overlap each other (after rescaling), despite the 100 times difference in aspect ratio d/t (diameter/thickness). These observations on the fi(θ) curves open a new possibility of mode shape engineering by designing and tuning the open angle θ of an incompletely clamped diaphragm. As demonstrated in Fig. 1c, for fully covered devices (θ = 0 only), one is limited in the frequency ratios between the modes and in degenerate mode pairs with small and random frequency splitting. With θ ≠ 0, one can adjust the θ value and choose many possible frequency ratios between different modes and the mode sequence can also be changed by engineering the θ values.
The observed fi(θ) behavior can be understood, very intuitively, by examining the interplay between the changes in both clamping conditions and resonator size, as θ increases. For a circular diaphragm clamped at the edge with flexural rigidity D and deflection w(r,φ), the associated potential energy is23 rdr for mode shapes that are azimuthally symmetric. By taking spatial derivatives we obtain an effective stiffness of
rdr for mode shapes that are azimuthally symmetric. By taking spatial derivatives we obtain an effective stiffness of  , where weff is the effective displacement of the entire diaphragm. For a partially clamped diaphragm, by analogy we approximate the effective stiffness as
, where weff is the effective displacement of the entire diaphragm. For a partially clamped diaphragm, by analogy we approximate the effective stiffness as  , or keff ∝ (2π − θ), assuming that the clamped arc (with a central angle (2π − θ)) provides all the restoring force. At small θ values, increasing θ mainly reduces the clamping arc length. As θ continues to increase, the reduction in device area (and thus the effective mass Meff) becomes more dominant and the frequency increases again (f ∝ [keff/Meff]1/2). Behavior of the higher modes can be understood similarly, with different keff and Meff values for different modes of the same device structure (see Supplementary Information S5 for detailed discussion). Figure 1e plots the value of [keff/Meff]1/2 as a function of θ. Clearly, between 0 and π, the frequency first decreases and then increases, capturing the main feature of this phenomenon.
, or keff ∝ (2π − θ), assuming that the clamped arc (with a central angle (2π − θ)) provides all the restoring force. At small θ values, increasing θ mainly reduces the clamping arc length. As θ continues to increase, the reduction in device area (and thus the effective mass Meff) becomes more dominant and the frequency increases again (f ∝ [keff/Meff]1/2). Behavior of the higher modes can be understood similarly, with different keff and Meff values for different modes of the same device structure (see Supplementary Information S5 for detailed discussion). Figure 1e plots the value of [keff/Meff]1/2 as a function of θ. Clearly, between 0 and π, the frequency first decreases and then increases, capturing the main feature of this phenomenon.
From Fig. 1d one can see that the effect of open angle θ upon the frequency curves is purely geometric – the shapes of fi(θ) curves only depend on θ and do not depend on actual dimensions of the devices (see Supplementary Information S6 for additional discussion). This fact allows one to quantitatively determine the device geometry (θ value) from the frequency ratios alone, regardless of device size. Figure 2a shows a device with θ ≈ 160° (measured from SEM and optical images), whose measured resonance spectrum is shown in Fig. 2b. The calculated frequency ratios for 0° < θ < 180° is plotted in Fig. 2c. By comparing calculated and measured frequency ratios we determine a θ value in the range of 155°−165°, in good agreement with the actual geometry of the device.
Quantifying device geometry through measured frequency ratios of multimode resonances from incomplete drumhead devices.
(a): SEM (perspective and top views) and optical images of a MoS2 resonator with incomplete drumhead structure. From the images we measure θ ≈ 160°. (b): The measured thermomechanical noise spectrum of the device, showing the first three resonance modes. Insets: Zoom-in on the individual resonances (measured at respective optimized locations on the device) showing the fitting to the model. (c): The comparison between calculated (solid curves) and measured frequency ratios between different resonance modes (measured values indicated by the horizontal dashed lines). The highlighted area denotes the θ range (155°–165°) in which the measured values intercept the calculated ones, showing good agreement with the θ value determined from the images.
The fact that such partial drumhead devices with free edges can have comparably high resonant performance as complete drumheads structures has important implications. First, this immediately increases the yield of functional devices by a factor of 2 or more (today in making suspended graphene and MoS2 2D structures by mechanical exfoliation, often ~50% suspended structures may have partially-covered geometries with free edges and yielding suspended MoS2 devices is particularly more challenging). More interestingly, edges of MoS2 crystal have distinct chemical properties different than the 2D surface and have been studied for applications such as electrocatalysis24,25,26,27,28. This enables one to preferentially functionalize the MoS2 resonator and create binding sites at selective locations (e.g., along the edges), offering opportunities for location-specific chemical and biological sensing. Furthermore, the edges of 2D crystals have unique electrical properties which make them interesting 1D sub-systems. For example, graphene edges have chirality-dependent electronic states29,30 and can remain gap-less even when a symmetry-breaking-caused energy gap is opened in the 2D bulk31. Such edge states are expected to carry dissipationless spin currents, as predicted from the topological properties of graphene as a quantum spin Hall insulator under spin-orbit coupling31,32,33,34. The properties of such spin-filtered 1D channels are expected to be sensitive to perturbations such as flexural curvature33, which can naturally couple to resonant motions in these partially-covered drumhead structures. In MoS2, the metallic 1D edge35 can be ferromagnetic for certain atomic configurations36. Both graphene and MoS2 edge states have been experimentally observed in substrate-supported samples35,37,38. With 1D electrical contacts directly accessing the edge of such 2D crystals39, these partial-drumhead resonators may soon help make new platforms for studying the coupling between mechanical, electrical and spin degrees of freedom in these 1D edge states, such as effects due to curvature33 and the interaction between spin-orbit and electron-phonon couplings40.
Asymmetry enables new devices – elliptic versus circular
We now explore the effects of geometric asymmetry and shape distortion of devices, by examining elliptic versus circular devices. Such imperfections may occur, sometime systematically, with challenging designs or imperfections in the manufacturing processes. Figure 3a shows three MoS2 diaphragms with the same thickness but different shapes – a circle and two ellipses. All three devices exhibit clear well-defined fundamental-mode resonances (Fig. 3b). The measured Qs show no observable dependence on the in-plane aspect ratio of the device (a/b) while the resonance frequency clearly increases with decreasing device size.
Elliptic MoS2 nanomechanical resonators and mapping of their multimode resonances.
(a): Optical and SEM images of three elliptic and circular resonators based on the same MoS2 nanosheet (t = 57.5 nm) (b): Measured thermomechanical resonances from device 1 (a = 6.81 μm, b = 5.89 μm), device 2 (d = 5.53 μm) and device 3 (a = 6.78 μm, b = 5.89 μm). (c): Wide range frequency spectra measured from both ecliptic devices (1 and 3). Insets: Spatially mapped resonance mode shapes for the first three resonance modes, measured by the scanning interferometric spectromicroscopy technique, in comparison to the simulated mode shapes in finite element modeling. Dashed lines outline the boundaries of the elliptic drumhead resonators.
When measured over a wider frequency range, both elliptic devices exhibit multimode resonances (Fig. 3c). We further spatially map the mode shapes of the observed multimode resonances, by performing the ‘scanning interferometric spectromicroscopy’ measurements, in which we focus on each individual resonance and scan the laser spot over the entire device surface (with a sub-micron spatial resolution) and measure the resonance amplitude versus the laser spot position. Figure 3c insets show the measured mode shapes vis-à-vis FEM simulations for all the resonances, demonstrating good agreement. We confirm that, due to the elliptic shape, the degeneracy in the 2nd and 3rd modes is lifted and the mode with nodal line along the semi-major axis has higher frequency than the mode with nodal line along the semi-minor axis.
To fully understand how the deviation from a circle to an ellipse affects the resonance frequencies, we perform FEM simulations for elliptic MoS2 diaphragm resonators with different aspect ratios (a/b, the ratio in length between the two semi-axes, see illustrations in Fig. 3b and Fig. 4). While resonance frequencies of elliptic diaphragms can be solved analytically with some approximation41,42, here we focus on the evolution of mode shapes and mode crossing. For ellipses, we use the notation p×q, the arrangement of anti-nodal motional domains (individual singly-connected continuous areas enclosed by nodal lines), to describe the mode shapes (see Fig. 4 legends). Note that this notation for ellipses is consistent with the conventions for describing multimode vibrations in rectangular diaphragms43. For circular devices, we use the traditional notation (n,m), where n and m refers to the number of nodal diameters and nodal circles (Fig. 4 legends).
Frequency scaling of the multimode resonances in the elliptic MoS2 nanomechanical resonators.
The frequency versus aspect ratio plot shows computed results for an elliptic MoS2 resonator with t = 57.5 nm, b = 5.53 μm (dimensions based on device (2) in Fig. 3) and a/b varying from 1/2 to 2 (with device shape illustrated for selected a/b values under the horizontal axis). The device orientation is shown on the a/b = 1.5 case under the axis and on the 1×4 mode shape at the top of the plot. Each curve (with distinct color and line type) shows the calculated f values for a particular mode shape (labeled on the corresponding curve). Double-headed arrows indicate the anti-crossing between the 1×3 and 3×1 modes at a/b = 1. Legend to the right gives the naming convention for the elliptic (top) and circular (bottom) mode shapes, with dashed lines representing the nodal lines. Inset: At higher frequencies, the 1×4/4×1 modes (blue curve, with extrapolations shown in dotted lines) and the 2×3/3×2 modes (red curve) cross at a/b = 1 with degeneracy in both frequency and mode shape.
From Fig. 4 we find that the lowest resonance frequency mode (dark yellow curve) is always the elliptic 1×1 mode, which corresponds to the circular (0,1) mode. The next lowest ones are the elliptic 1×2 and 2×1 modes (red/blue curves), corresponding to the circular (1,1) mode. At a/b = 1 these two modes degenerate and the curves cross each other. All these 3 modes are observed in Fig. 3c for both elliptic devices, showing good agreement between measurement and theory in both mode sequence and mode shapes.
The next lowest modes near a/b = 1, 1×3 and 3×1 (wine and magenta curves) show more complicated behavior. As a/b approaches 1, their mode shapes deform, with the center motional domains elongating into dumbbells and eventually bifurcating, becoming essentially the elliptic 2×2 modes (olive curve) at a/b = 1 (corresponding to the circular (2,1) mode). In contrast to the 1×2 and 2×1 modes, where the mode shapes continue on both sides of a/b = 1, here the 1×3 and 3×1 modes on one side do not continue into the same mode shapes on the other side (double-headed arrows in Fig. 4). Indeed, the higher frequency 3×1 and 1×3 modes (magenta-wine curve), whose three motional domains align along the semi-minor axis, merge into the circular (0,2) mode at a/b = 1.
The evolution of the mode shapes also affects how the curves approach each other upon degeneracy. When the mode shapes are retained in both regimes across a/b = 1, as in the 1×2 – 2×1 crossing, the curves (red-blue) simply cross, retaining individual slopes. When the mode shapes also degenerate (one mode shape evolves into another), as in the 1×3 – 2×2 and 1×4 – 2×3 (Fig. 4 inset) crossing, the curves become tangent to each other. When a certain mode evolves into different shapes when approaching a/b = 1 from opposite directions, such as 1×3 → 2×2 from a/b < 1 and 1 × 3 → (0,2) from a/b > 1, anticrossing is observed (doubled-headed arrows in Fig. 4).
By examining the mode evolutions, we clearly demonstrate and verify that circular devices are in fact one special case of elliptic devices, with some circular modes being the degenerate case of multiple elliptic modes. As a result, any broken symmetry in shape on a circular resonator can lift its degeneracy and dictate the resonant modes to take particular orientations, split in frequency, or even bifurcate into different elliptic mode shapes. Such effects are practically unavoidable in intentionally designed circular resonators, leading to random, undesirable splitting of the degenerate modes. The results here suggest that designing the resonators to be elliptic can alleviate such problems by lifting the degeneracy in a controlled manner.
Lifting resonance degeneracy is important for realizing next-generation devices for spatially-resolved resonant sensing of surface adsorbates. Study of surface adsorption on 1D NEMS devices has already revealed a number of interesting phenomena such as low-dimensional phase transition44,45 and surface adsorbate fluctuations46,47. By monitoring multiple resonance modes of a MEMS/NEMS resonator, it is possible to simultaneously determine the mass and position of the adsorbed species48,49,50,51. Such functionality, so far only demonstrated in 1D resonators, could be extended to 2D resonant sensors52. Spatially-resolved detection and dynamical monitoring of surface adsorbates appear to be more interesting on 2D platforms because the additional degree of freedom allows for richer position responsivity coupled to multiple 2D mode shapes, thus enabling studies of intriguing phenomena such as on-device cell division and 2D chemical reactions53 with simultaneous mass and position detection of individual particles. In order to unambiguously determine the adsorbate position, it is desirable that any random degeneracy be removed from the multimode characteristics of the resonant sensor. In this case, perfectly circular resonators become unfriendly for resolving positions of adsorbates, for having the highest degree of symmetry and degeneracy among 2D geometries. Elliptic resonators demonstrated in Fig. 4 systematically lift the undesired resonance degeneracy and are thus better suited for multimode resonant sensing. We envisage, exploring device geometries with even higher degree of asymmetry (e.g., specially-engineered scalene triangular resonators) can further control the mode shapes of degenerate resonances, completely removing the spatial ambiguity in 2D multimode monitoring of adsorbates.
Conclusions
In summary, we have experimentally demonstrated that MoS2 2D nanomechanical resonators with structural nonidealities and asymmetries, compared with their ‘ideal’ counterparts, can engender new multimode resonance characteristics. Given the occurrences in large populations of exfoliated devices made of emerging 2D materials (including graphene, h-BN and various TMDCs), observed effects from geometrical nonidealities in this study have important implications. It shows that suspended 2D structures appearing to be ‘imperfect’ should not be deemed unworthy, instead they make very interesting devices that can offer new functions (e.g., enabled by the free edges). Collectively, these 2D structures with ‘nonideal’ appearances or broken symmetries form new families of resonators with versatile dispersion relations (of multimode frequency versus geometry). It also demonstrates that geometry can be powerful for tuning the device performance, such as resonance frequencies, mode shapes, mode splitting and frequency spacing. It is therefore intriguing to engineer devices with ‘customized’ resonance behavior, such as specified frequency ratios between the different resonance modes, by tailoring device geometric parameters. This can be a useful tool, for example, in designing multimode and nonlinear resonant components in micromechanical circuits, where the ability of creating arbitrary ratios between resonance frequencies of the different modes is desirable54. The capability of controlling mode shapes can also be useful in designing resonators with position-specific surface adsorption sensing and manipulation capabilities49,51. We conclude that visual appearance of MoS2 and other 2D devices should not be a criterion for judging the devices; embracing and exploiting structural nonidealities and broken symmetries can benefit future device innovations. Looking forward, devices with these interesting structural nonidealities will not be limited to random yield in hand-craft exfoliation on small chips, but can be intentionally designed – such opportunities may soon be enabled by advancements in high-precision deterministic transfer methods7,8,9,10,11 and large-area synthesis of MoS2 with improving control (e.g., of size, shape, crystalline orientation)55,56,57,58.
Methods
Device fabrication
The devices are fabricated using the mechanical exfoliation method. First, we perform optical lithography followed by buffered oxide etch (BOE) to pattern arrays of microscale trenches of various sizes and shapes on a 290 nm-thick silicon dioxide (SiO2) layer thermally grown on a silicon (Si) wafer. The BOE etch time is controlled such that the entire depth (290 nm) of SiO2 is removed, exposing the flat Si surface underneath. We then exfoliate MoS2 flakes onto the structured wafer. Flakes covering the microtrenches form drumhead-structured nanomechanical resonators.
Mechanical exfoliation of MoS2 typically results in small flakes (i.e., often smaller compared to exfoliated graphene flakes on the same substrate using exactly the same procedure). When the flakes are small (with respect to the microtrenches), they are likely to form devices where the microtrenches are not fully covered by the MoS2 nanosheets. Incomplete drumheads with partially-clamped boundaries occur, creating incompletely-clamped drumhead nanomechanical resonators. Supplementary Fig. S1 shows a schematic of the device fabrication process and the resulting device geometries.
Interferometric motion detection system
The mechanical resonances of the nonideally or imperfectly structured MoS2 resonators are measured using a custom-built system with ultrasensitive optical readout techniques21,22. The schematic of the measurement system is shown in Supplementary Fig. S2.
In our custom-built interferometry system, the laser beam from a 633 nm He-Ne laser first goes through a beam expander. It is then focused by a 50× microscope objective lens with optical window correction (NA = 0.5) onto the surface of the MoS2 nanosheet (the spot size is ~1 μm). The interference between the light waves reflected from the suspended MoS2 nanosheet and the underneath Si surface determines the intensity of the total reflected light. The undriven thermomechanical motions (i.e., Brownian motions, as dictated by the fluctuation-dissipation theorem) of the MoS2 nanosheet modulate the interference signal. The interferometric signal is detected by a low-noise photodetector (PD) and then sent to a spectrum analyzer. The high sensitivity of the measurement system allows us to detect the minimal vibrations of the MoS2 nanosheet arising from its fundamental thermomechanical (Brownian) motions and thus find its resonances without any external driving. We also adjust our on-device laser power to be ≤700 μW such that the heating effect is negligible (no heating-induced frequency change within the power range used), while maintaining a good signal-to-noise ratio22. All our measurements are conducted in moderate vacuum (~6 mTorr) at room temperature.
References
Geim, A. K. & Novoselov, K. S. The rise of graphene. Nat. Mater. 6, 183–191 (2007).
Geim, A. K. Graphene: Status and prospects. Science 324, 1530–1534 (2009).
Wang, Q. H., Kalantar-Zadeh, K., Kis, A., Coleman, J. N. & Strano, M. S. Electronics and optoelectronics of two-dimensional transition metal dichalcogenides. Nat. Nanotechnol. 7, 699–712 (2012).
Butler, S. Z. et al. Progress, challenges and opportunities in two-dimensional materials beyond graphene. ACS Nano 7, 2898–2926 (2013).
Novoselov, K. S. Nobel lecture: graphene: materials in the flatland. Rev. Mod. Phys. 83, 837–849 (2011).
Novoselov, K. S. et al. Two-dimensional atomic crystals. Proc. Natl. Acad. Sci. 102, 10451–10453 (2005).
Britnell, L. et al. Field-effect tunneling transistor based on vertical graphene heterostructures. Science 335, 947–950 (2012).
Dean, C. R. et al. Boron nitride substrates for high-quality graphene electronics. Nat. Nanotechnol. 5, 722–726 (2010).
Georgiou, T. et al. Vertical field-effect transistor based on graphene-WS2 heterostructures for flexible and transparent electronics. Nat. Nanotechnol. 8, 100–103 (2013).
Haigh, S. J. et al. Cross-sectional imaging of individual layers and buried interfaces of graphene-based heterostructures and superlattices. Nat. Mater. 11, 764–767 (2012).
Mayorov, A. S. et al. Micrometer-scale ballistic transport in encapsulated graphene at room temperature. Nano Lett. 11, 2396–2399 (2011).
He, K., Poole, C., Mak, K. F. & Shan, J. Experimental demonstration of continuous electronic structure tuning via strain in atomically thin MoS2 . Nano Lett. 13, 2931–2936 (2013).
Zhu, C. R. et al. Strain tuning of optical emission energy and polarization in monolayer and bilayer MoS2 . Phys. Rev. B 88, 121301 (2013).
Conley, H. J. et al. Bandgap engineering of strained monolayer and bilayer MoS2 . Nano Lett. 13, 3626–3630 (2013).
Jiang, J.-W., Park, H. S. & Rabczuk, T. MoS2 nanoresonators: intrinsically better than graphene? arXiv:cond-mat/1401.0576 (2014).
Carr, D. W., Sekaric, L. & Craighead, H. G. Measurement of nanomechanical resonant structures in single-crystal silicon. J. Vac. Sci. Technol. B 16, 3821 (1998).
Ilic, B., Krylov, S., Aubin, K., Reichenbach, R. & Craighead, H. G. Optical excitation of nanoelectromechanical oscillators. Appl. Phys. Lett. 86, 193114 (2005).
Karabacak, D., Kouh, T. & Ekinci, K. L. Analysis of optical interferometric displacement detection in nanoelectromechanical systems. J. Appl. Phys. 98, 124309 (2005).
Karabalin, R. B. et al. Piezoelectric nanoelectromechanical resonators based on aluminum nitride thin films. Appl. Phys. Lett. 95, 103111 (2009).
Hiebert, W. K., Vick, D., Sauer, V. & Freeman, M. R. Optical interferometric displacement calibration and thermomechanical noise detection in bulk focused ion beam-fabricated nanoelectromechanical systems. J. Micromech. Microeng. 20, 115038 (2010).
Lee, J. & Feng, P. X.-L. High frequency graphene nanomechanical resonators and transducers. Proc. IEEE Int. Freq. Control Symp. 10.1109/FCS.2012.6243742 (2012).
Lee, J., Wang, Z., He, K., Shan, J. & Feng, P. X.-L. High frequency MoS2 nanomechanical resonators. ACS Nano 7, 6086–6091 (2013).
Weaver, W., Jr, Timoshenko, S. P. & Young, D. H. Vibration Problems in Engineering. John Wiley & Sons, 1990.
Karunadasa, H. I. et al. A Molecular MoS2 edge site mimic for catalytic hydrogen generation. Science 335, 698–702 (2012).
Kibsgaard, J., Chen, Z., Reinecke, B. N. & Jaramillo, T. F. Engineering the surface structure of MoS2 to preferentially expose active edge sites for electrocatalysis. Nat. Mater. 11, 963–969 (2012).
Xie, J. et al. Defect-rich MoS2 ultrathin nanosheets with additional active edge sites for enhanced electrocatalytic hydrogen evolution. Adv. Mater. 25, 5807–5813 (2013).
Lukowski, M. A. et al. Enhanced hydrogen evolution catalysis from chemically exfoliated metallic MoS2 nanosheets. J. Am. Chem. Soc. 135, 10274–10277 (2013).
Choi, W. I., Wood, B. C., Schwegler, E. & Ogitsu, T. Site-dependent free energy barrier for proton reduction on MoS2 edges. J. Phys. Chem. C 117, 21772–21777 (2013).
Jia, X., Campos-Delgado, J., Terrones, M., Meunier, V. & Dresselhaus, M. S. Graphene edges: a review of their fabrication and characterization. Nanoscale 3, 86–95 (2011).
Zhang, X., Xin, J. & Ding, F. The edges of graphene. Nanoscale 5, 2556–2569 (2013).
Yao, W., Yang, S. A. & Niu, Q. Edge states in graphene: from gapped flat-band to gapless chiral modes. Phys. Rev. Lett. 102, 096801 (2009).
Yao, Y., Ye, F., Qi, X.-L., Zhang, S.-C. & Fang, Z. Spin-orbit gap of graphene: First-principles calculations. Phys. Rev. B 75, 041401 (2007).
Gosálbez-Martínez, D., Soriano, D., Palacios, J. J. & Fernández-Rossier, J. Spin-filtered edge states in graphene. Solid State Commun. 152, 1469–1476 (2012).
Kou, L. et al. Graphene-based topological insulator with an intrinsic bulk band gap above room temperature. Nano Lett. Article ASAP 10.1021/nl4037214 (2013).
Bollinger, M. V. et al. One-dimensional metallic edge states in MoS2 . Phys. Rev. Lett. 87, 196803 (2001).
Vojvodic, A., Hinnemann, B. & Nørskov, J. K. Magnetic edge states in MoS2 characterized using density-functional theory. Phys. Rev. B 80, 125416 (2009).
Kobayashi, Y., Fukui, K., Enoki, T., Kusakabe, K. & Kaburagi, Y. Observation of zigzag and armchair edges of graphite using scanning tunneling microscopy and spectroscopy. Phys. Rev. B 71, 193406 (2005).
Tao, C. et al. Spatially resolving edge states of chiral graphene nanoribbons. Nat. Phys. 7, 616–620 (2011).
Wang, L. et al. One-dimensional electrical contact to a two-dimensional material. Science 342, 614–617 (2013).
Ochoa, H., Castro Neto, A. H., Fal'ko, V. I. & Guinea, F. Spin-orbit coupling assisted by flexural phonons in graphene. Phys. Rev. B 86, 245411 (2012).
Shibaoka, Y. On the transverse vibration of an elliptic plate with clamped edge. J. Phys. Soc. Jpn. 11, 797–803 (1956).
McNitt, R. P. Free vibration of a damped elliptical plate. J. Aerospace Sci. 29, 1124–1125 (1962).
Graff, K. F. Wave Motion in Elastic Solids. Courier Dover Publications, 1975.
Wang, Z. et al. Phase transitions of adsorbed atoms on the surface of a carbon nanotube. Science 327, 552–555 (2010).
Lee, H.-C. et al. Kr and 4He adsorption on individual suspended single-walled carbon nanotubes. J. Low Temp. Phys. 169, 338–349 (2012).
Yang, Y. T., Callegari, C., Feng, X.-L. & Roukes, M. L. Surface adsorbate fluctuations and noise in nanoelectromechanical systems. Nano Lett. 11, 1753–1759 (2011).
Atalaya, J., Isacsson, A. & Dykman, M. I. Diffusion-induced dephasing in nanomechanical resonators. Phys. Rev. B 83, 045419 (2011).
Dohn, S., Sandberg, R., Svendsen, W. & Boisen, A. Enhanced functionality of cantilever based mass sensors using higher modes. Appl. Phys. Lett. 86, 233501 (2005).
Dohn, S., Svendsen, W., Boisen, A. & Hansen, O. Mass and position determination of attached particles on cantilever based mass sensors. Rev. Sci. Instrum. 78, 103303 (2007).
Dohn, S., Schmid, S., Amiot, F. & Boisen, A. Position and mass determination of multiple particles using cantilever based mass sensors. Appl. Phys. Lett. 97, 044103 (2010).
Hanay, M. S. et al. Single-protein nanomechanical mass spectrometry in real time. Nat. Nanotechnol. 7, 602–608 (2012).
Atalaya, J., Kinaret, J. M. & Isacsson, A. Nanomechanical mass measurement using nonlinear response of a graphene membrane. Europhys. Lett. 91, 48001 (2010).
Heredia-Guerrero, J. A., San-Miguel, M. A., Sansom, M. S. P., Heredia, A. & Benítez, J. J. Chemical reactions in 2D: self-assembly and self-esterification of 9(10),16-dihydroxypalmitic acid on mica surface. Langmuir 25, 6869–6874 (2009).
Nguyen, C. T.-C. MEMS technology for timing and frequency control. IEEE Trans. Ultrason. Ferr. & Freq. Contr. 54, 251–270 (2007).
Zhan, Y., Liu, Z., Najmaei, S., Ajayan, P. M. & Lou, J. Large-area vapor-phase growth and characterization of MoS2 atomic layers on a SiO2 substrate. Small 8, 966–971 (2012).
Shi, Y. et al. van der Waals epitaxy of MoS2 layers using graphene as growth templates. Nano Lett. 12, 2784–2791 (2012).
van der Zande, A. M. et al. Grains and grain boundaries in highly crystalline monolayer molybdenum disulphide. Nat. Mater. 12, 554–561 (2013).
Yu, Y. et al. Controlled Scalable Synthesis of Uniform, High-Quality Monolayer and Few-Layer MoS2 films. Sci. Rep. 3, 1866; 10.1016/srep01866 (2013) .
Acknowledgements
We are grateful to Case School of Engineering and the T. Keith Glennan Fellowship Program for the financial support.
Author information
Authors and Affiliations
Contributions
Z.W., J.L. and K.H. fabricated the devices. Z.W., J.L. and P.X.L.F. performed resonance measurements and device characterization and analyzed the data. Z.W. and P.X.L.F. developed the modeling of multimode and shape-dependent resonance scaling. Z.W. and P.X.L.F. wrote the manuscript. J.S. and J.L. contributed to revising the manuscript. All authors discussed about the results and reviewed the manuscript. P.X.L.F. conceived the experiment and supervised the project.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Electronic supplementary material
Supplementary Information
Supplementary Information
Rights and permissions
This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivs 3.0 Unported License. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-nd/3.0/
About this article
Cite this article
Wang, Z., Lee, J., He, K. et al. Embracing Structural Nonidealities and Asymmetries in Two-Dimensional Nanomechanical Resonators. Sci Rep 4, 3919 (2014). https://doi.org/10.1038/srep03919
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep03919
This article is cited by
-
Splitting of vibration mode in an imperfect submicron circular plate
Acta Mechanica (2021)
-
Manipulation of Coherent Optical Propagation Based on Monolayer MoS2 Resonator
Photonic Sensors (2019)
-
Hexagonal boron nitride nanomechanical resonators with spatially visualized motion
Microsystems & Nanoengineering (2017)
-
Tunable phonon-cavity coupling in graphene membranes
Nature Nanotechnology (2016)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.