Abstract
The focusing performance of a multilayer Laue lens (MLL) with 43.4 μm aperture, 4 nm finest zone width and 4.2 mm focal length at 12 keV was characterized with X-rays using ptychography method. The reconstructed probe shows a full-width-at-half-maximum (FWHM) peak size of 11.2 nm. The obtained X-ray wavefront shows excellent agreement with the dynamical calculations, exhibiting aberrations less than 0.3 wave period, which ensures the MLL capable of producing a diffraction-limited focus while offering a sufficient working distance. This achievement opens up opportunities of incorporating a variety of in-situ experiments into ultra high-resolution X-ray microscopy studies.
Similar content being viewed by others
Introduction
Hard X-ray microscopy provides a unique opportunity to perform studies of materials at the nanometer scale and offers a suite of techniques such as fluorescence, absorption, differential phase contrast, diffraction and spectroscopy. All these analytic techniques complement each other and yield a comprehensive map of structural, chemical and elemental properties of a specimen. To achieve sufficient spatial resolution and contrast requires high-efficiency nanofocusing optics to determine the smallest spot size of the focused beam and deliver the desired photon density. A variety of nanofocusing optics, including waveguide1, parabolic refractive lens2, multilayer Laue lenses3 and multilayer mirror4, have been theoretically studied with the intent to focus hard X-rays to the sub-10 nm level. Practical implementation, however, remains a challenging task. Sub-10 nm resolution using a Fresnel zone plate has been successfully demonstrated with soft X-rays5, while extending the same capability to hard X-ray regime is still ongoing6. Developments of reflective X-ray optics reduced the focal spot size down to 7 nm at 20 keV using an adaptive optic to compensate phase errors of the focusing mirror7. Recently, compound optics demonstrated sub-5 nm 2D focus through a combination of Kirkpatrick-Baez (KB) mirrors and a multilayer zone plate with 1.6 μm aperture and 50 μm focal length at 7.9 keV8. We have pursued the development of multilayer Laue lens (MLL), a diffractive optic, capable of achieving 1 nm focusing with high efficiency3. Using MLLs, 16 nm line focus with 31% efficiency at 19.5 keV9 and 25 nm × 27 nm 2D focus with 2% efficiency at 12 keV10 have been demonstrated. A prototype microscope using MLLs has been constructed11 and used for materials science investigations12,13.
To continue the development of MLL optics and push the focal spot size into the sub-10 nm regime, it is critical to perform accurate and quantitative characterization of optics performance. In recent years, ptychography14,15 has been used as a robust, lensless imaging tool, which has been applied to numerous scientific problems and focusing optics characterizations. Ptychography is a scanning version of the coherent diffraction imaging (CDI) method. A specimen is scanned across a confined X-ray beam with substantial overlap in adjacent scan positions. The redundant information encoded in far-field diffraction patterns constrains the iterative phase-retrieval algorithm to simultaneous reconstructions of a complex transmission function of the sample and the X-ray wavefront. The obtained complex-valued wavefront represents the complete focusing performance of a lens and is highly sensitive to optics aberrations or misalignments. Since the recovered wavefront can be numerically propagated to any plane of interest, a ptychography measurement does not need to be performed at the exact location of a focal plane, therefore relaxing the alignment complexity of a nanofocusing system. Ptychography has been proven to provide robust and reliable X-ray wavefront measurements for KB mirrors16, compound refractive lens17, kinoform lens18 and zone plate19 using synchrotron radiation, as well as X-ray free electron laser pulses20.
Here, we report an 11 nm focus achieved at 12 keV with an MLL characterized by the ptychography method. The achievement of such a small focus with a large lens aperture of 43.4 μm marks a significant step towards development of nanofocusing optics with high efficiency and long working distance enabling diverse scientific applications. The reconstructed X-ray wavefront shows excellent agreement with theoretical simulations using dynamical diffraction theory. The analyzed phase deviation, when compared with a perfect lens, matches the zone placement error from an independent metrology measurement. Our comprehensively cross-checked results confirm the accuracy of ptychography analysis and experimentally demonstrate that a focus near to its diffraction limit has been achieved with a large-aperture MLL.
Results
The MLL studied in this work contains 6510 alternating flat layers of Si and WSi2, spanning 40% of a full MLL, as shown in Fig. 1. The partial MLL structure is used to reduce the apodization effect and extend the achievable working distance21. The MLL has 4 nm finest zone width and 43.4 μm aperture size, which is significantly larger than apertures of previously reported MLLs8,10,22. This lens provides 4.2 mm focal length at 12 keV. Fig. 1c shows that 12 marker layers were deposited within the multilayer structure. Comparison of the actual marker layer positions against the ideal positions provides an effective method to quantify the accuracy of zone placements23. Using this method, we determined, with a precision better than 1 nm, that the MLL zone placement error is ±2 nm over the 43.4 μm aperture.
Scanning electron microscope (SEM) images of the MLL.
Top view (a) and side view (b) of the focused-ion beam (FIB)-etched MLL with 4 nm finest zone width and 43.4 μm aperture size, within a 6 μm thick and 120 μm wide window. (c) 12 marker layers inserted into the multilayer structure were used to monitor growth accuracy and estimate zone placement error.
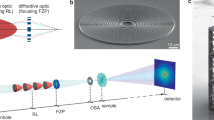
The ptychography experiment was performed at beamline 34-ID-C of the Advanced Photon Source at Argonne National Laboratory, using coherent 12 keV X-rays. A dedicated instrument was constructed for ptychography measurements. A schematic view of the experimental setup is shown in Fig. 2. To maximize the diffraction signal from a 1D focused beam, a grating-shape gold test-pattern sample with 1.6 μm thickness was mounted close to the focal plane. To reduce potential reconstruction artifacts arising from translational symmetry, scan positions followed a concentric trajectory24 with 50 nm radial step size over a 0.5 μm × 2 μm area, as shown in Fig. 3b. A 2D scan procedure was used to characterize the focused X-rays and the test pattern, both of which represent 1D structures, based on the following considerations. First, although the translation diversity in ptychography has been reported to alleviate the uniqueness problem of phase retrieval algorithm for 1D cases18, 2D overlapping redundancy improves robustness and yields better convergence16. Second, the gold test sample has rough sidewalls (Supplementary Fig. S1), so that it cannot be considered as a pure 1D structure. Third, the incident X-ray beam for the experiment, propagated 15 cm from beam-defining slits, deviates from a plane wave when arriving at the MLL optic. Variations in the horizontal direction are exhibited (Supplementary Fig. S2). Consequently, both the sample and the X-ray wavefront have to be treated as 2D structures, thus 2D ptychography scans were appropriate for data acquisition and analysis.
Experimental setup for the ptychography measurement.
The incident 12 keV X-ray illumination is selected by 10 μm × 45 μm entrance slits placed 15 cm in front of the MLL. A gold order-sorting aperture (OSA) with a 20 μm × 10 μm aperture and 50 μm thickness and a grating-shape test-pattern sample are placed near the MLL focal plane. The test-pattern sample is scanned in the XY plane, while far-field diffraction patterns are recorded by a pixel-array detector placed 0.97 m downstream.
Experimental data and reconstructed sample image.
(a) A typical frame of a far-field diffraction pattern displayed on a logarithmic intensity scale. (b) An SEM image of the test-pattern sample. Red dots indicate scan positions. The green box shows the reconstruction field of view (~2.4 × 3.8 μm). (c) A line profile of absorption contrast, corresponding to the integrated photon counts inside the central streak within the dashed red box in (a), plotted against the vertical scan positions. (d) The reconstructed image of the sample grating with amplitude displayed in brightness and phase displayed in hue. (e) Peak-fitting of the obtained thickness histogram estimates that the sample thickness is 1653 ± 136 nm, which agrees with the manufacturer's thickness specification of 1600 ± 160 nm.
Data were acquired after the instrument enclosure reached its thermal equilibrium. A typical far-field diffraction pattern is shown in Fig. 3a. The integrated photon count inside the central streak for each 2D diffraction pattern, as indicated by the dashed red box in Fig. 3a, provides absorption contrast of the sample. Fig. 3c plots the integrated transmission signal, which shows the line structure of the sample grating. The vertical streaks outside the central stripe (shown in Fig. 3a) and the uneven spacing between the gold gratings (shown in Fig. 3c) arise from artifacts of the test-pattern sample, which is described in Supplementary Information and shown in Supplementary Fig. S1.
Fig. 3d shows the reconstructed gold grating structure with amplitude and phase represented by brightness and hue, respectively. The sample thickness Δz can be estimated from reconstructed phases ϕ by ϕ = −2πδΔz/λ, where δ is the real part of the gold refractive index deviation from unity. Two peaks were observed in the obtained thickness histogram (Fig. 3e): one peak centered at zero thickness represents the empty region between gratings and the other peak corresponds to an averaged grating thickness of 1653 ± 136 nm, consistent with the manufacturer's thickness specification of 1600 ± 160 nm.
The complex-valued focused X-ray wavefront was reconstructed simultaneously with the gold grating image. At the measurement plane, the X-ray beam width is about 140 nm. The ptychography scan with 50 nm radial step size ensures an overlapping ratio of at least 64%, which is a favorable condition for ptychography25. Fig. 4a shows the recovered X-ray wavefront at the focal plane, which is numerically propagated 12.25 μm downstream from the measurement plane. The FWHM of the intensity line plot at the focal plane is 11.2 nm, which agrees extremely well with the estimated value from theoretical simulation (shown in Fig. 4b). Moreover, the logarithmic intensity plots (Fig. 4c) show that the reconstructed probe matches with simulation up to its fifth-order satellite peak on the left side of the main peak and its forth-order satellite peak on the right side, respectively. To the best of our knowledge, this is the most accurate measurement achieved among reported nanofocusing characterizations. It should be noted that the zone placement error obtained from the SEM measurement has been incorporated into the theoretical calculation based on the dynamical diffraction model3 in the comparison. Fig. 4d and e illustrate the propagation series of the reconstructed probe and the simulated probe with zone placement aberrations, respectively, where the characteristic features show excellent agreement. All these pieces of evidence confirm that a reliable and accurate X-ray wavefront is obtained. The measured focusing efficiency is 15%, which is close to the theoretical value 18%.
Reconstructed X-ray wavefront.
(a) The reconstructed X-ray wavefront at its focal plane with the amplitude displayed in brightness and phase displayed in hue. (b) A line focus with 11.2 nm FWHM is obtained, which agrees extremely well with the theoretical simulation incorporating the measured zone placement error. (c) The satellite peaks of the reconstructed probe match very well with the simulation result on a logarithmic intensity plot. (d) Starting from the measurement plane, the reconstructed wavefront is propagated from −100 μm to +100 μm in 250 nm steps. The focal plane is located 12.25 μm downstream from the measurement plane. (e) The propagation series of the simulated probe. The characteristic features in (d) and (e) show excellent agreement.
For more quantified aberration details of this nanofocusing optic, the reconstructed X-ray wavefront was back-propagated to the MLL pupil plane. As shown in Fig. 5a and b, the corresponding amplitude and phase are in good agreement with the simulated exit wave of a perfect MLL at the pupil plane. The difference between two phase curves in Fig. 5b quantifies the phase deviation of the reconstruction from a perfect lens, which is plotted as the red curve in Fig. 5c. The marker layer locations, determined from SEM measurements, are used to evaluate zone displacements Δd at specific aperture positions with expected zone width Δrn. Consequently, the phase error deviation from a perfect lens can also be estimated by πΔd/Δrn, shown as the black curve in Fig. 5c. The excellent agreement of these two independent phase-error measurements provides a further confirmation that the ptychography method accurately analyzes the aberrations of the MLL optic. State-of-the-art multilayer focusing mirrors deliver a wavefront with about 1.3 wave periods of distortion, which can be corrected by deformable adaptive mirrors with a controllability range of 0.1 wave period7. Fig. 5c shows that the MLL used in our experiment without in-situ adaptive optics has a phase distortion variance of ±1 radians, corresponding to 0.3 wave period. According to Rayleigh's quarter-wavelength rule26, this 0.3 wave period distortion allows the MLL to produce a focus very close to the diffraction limit.
Amplitude and phase errors at the MLL pupil plane.
Amplitude (a) and phase (b) comparison of the reconstructed and simulated probes at the MLL pupil plane. (c) The phase difference between reconstruction and simulation (the red curve) is consistent with the phase error estimated from the zone displacements of marker layer, determined by SEM measurements (the black curve).
Discussion
The aperture of the MLL measured in this experiment is approaching that of zone plates for hard X-rays. A large-aperture MLL permits a sufficient working distance to insert an OSA. Our prior works10,13, carried out using MLLs with smaller apertures, could not employ an OSA due to limited working distances. As a consequence, only specially prepared samples with isolated regions of interest could be used, to avoid signals from X-rays transmitted through MLLs. A long working distance is also extremely beneficial for in-situ experiments that require space for environmental cells27,28. MLLs with large apertures also provide opportunities for using MLLs as an objective optic for a transmission X-ray microscope, leading to a dramatic enhancement in resolution and efficiency, particularly for high X-ray energies.
In summary, an 11.2 nm hard X-ray focus with 15% efficiency was achieved using a precisely grown MLL with 4 nm finest zone width and 43.4 μm aperture. Ptychography analysis, cross-checked with dynamical diffraction simulation and an independent metrology measurement, revealed a low optical aberration of 0.3 wave period, corresponding to focusing performance very close to the diffraction limit. Successful fabrication of an ultra-high resolution MLL with a sufficiently large working distance marks a significant achievement in X-ray optics, presenting exciting scientific opportunities for diverse X-ray microscopy applications.
Methods
MLL fabrication
A magnetron sputtering method was used to grow MLL thin-films29, by alternating Si and WSi2 layers according to the zone plate law. In addition to argon gas, nitrogen was also used to reduce the accumulated film-stress in the multilayer stack. After the deposition, the multilayer was patterned and etched via the reactive-ion-etching method to a bar with around 100 μm width. The FIB method was then employed to reduce the width to about 5 μm within a 100 μm window. In order to minimize the surface damage, multiple steps with progressively reduced beam power were taken during the FIB milling process. Marker layers, each of which consists of 3 repeated layers of WSi2, were inserted into the multilayer structure to monitor accumulated growth accuracy and estimate zone placement error.
Experimental setup
The MLL instrument was installed at about 54 m from the center of the 34-ID-C undulator and 27 m from the horizontal source-defining slits. At 12 keV, with a 26 μm vertical source size and a 100 μm horizontal slit setting, the transverse coherence length at the beam-defining slits plane is 14 μm × 113 μm. The beam-defining slits were set to 10 μm × 45 μm to select the coherent portion of the incident illumination and sufficiently cover the MLL vertical aperture. The measurement was conducted with a 10 μm section near the center of the 120 μm wide MLL window. The OSA was a 10 μm × 20 μm FIB-drilled hole on a 50 μm-thick gold foil, which was mounted about 300 μm in front of the sample. A resolution test pattern (X500-200-16, Xradia Inc.) was used as the sample. A Timepix pixel-array detector with 512 × 512 pixels and a 55 μm pixel size (QTPX-262k, Amsterdam Scientic Instruments) provided single-photon counting capability for data acquisition. A double-wall isolation enclosure was used to protect the microscope from acoustic and thermal fluctuations. Data were collected 18 hours after closing doors of the isolation enclosure and the experimental hutch. To accommodate the dynamic range of the detector and to obtain decent signal-to-noise ratio, each frame of the ptychography scan was accumulated 30 times with 0.1 second exposures. Each complete 2D ptychography scan took about 30 minutes. The detector was placed 0.97 m away from the sample. A 128 × 512 pixel array cropped from each diffraction pattern was fed into a reconstruction algorithm, which gave a real-space pixel size of 14.0 nm × 3.5 nm in reconstructed images.
Reconstruction details
The detector contains 4 modules of 256 × 256 pixels, while the pixels at the module boundary are 3 times as large as regular pixel size. Instead of dividing their readings evenly into 3 pixels, the boundary pixels were set to zero. The parasitic scattering signal from the OSA edge slightly varies from one frame to another, so that all 329 frames of far-field diffraction patterns from an entire ptychography scan were summed together to accurately determine the pixels occupied by the parasitic flare, which were then masked out from each frame (details are shown in Supplementary Fig. S3). Both the pixels on module boundaries and those located under parasitic flares were allowed to float during the iterative reconstruction process. Image recovery was conducted using the Difference Map formulation for ptychography15. Each reconstruction ran 100 iterations. The last 20 iteration outputs were averaged to eliminate high-frequency fluctuation. The object always started with a randomly assigned complex array and was updated from the first iteration. In the first trial, a Gaussian-shape line structure with about 20 nm width was used as the initial guess of the probe. The probe updating always started after 5 iterations. The output probe from the first trial was inherited as the starting guess for the next trial. After 5 rounds of preliminary runs, the probe function was stabilized, which was then used as the start for the next 10 runs with individually initiated random objects. These 10 results were averaged to give the final images.
References
Bergemann, C., Keymeulen, H. & van der Veen, J. Focusing X-ray beams to nanometer dimensions. Phys. Rev. Lett. 91, 204801 (2003).
Schroer, C. & Lengeler, B. Focusing hard x rays to nanometer dimensions by adiabatically focusing lenses. Phys. Rev. Lett. 94, 054802 (2005).
Yan, H. et al. Takagi-taupin description of X-ray dynamical diffraction from diffractive optics with large numerical aperture. Phys. Rev. B 76, 115438 (2007).
Morawe, C., Guigay, J., Mocella, V. & Ferrero, C. An analytical approach to estimating aberrations in curved multilayer optics for hard X-rays: 2. interpretation and application to focusing experiments. Opt. Express 16, 16138–16150 (2008).
Chao, W. et al. Real space soft X-ray imaging at 10 nm spatial resolution. Opt. Express 20, 9777–9783 (2012).
Chen, T. et al. Full-field microimaging with 8 kev X-rays achieves a spatial resolution better than 20 nm. Opt. Express 19, 19919–19924 (2011).
Mimura, H. et al. Breaking the 10 nm barrier in hard-X-ray focusing. Nature Phys. 6, 122–125 (2010).
Doring, F. et al. Sub-5 nm hard X-ray point focusing by a combined Kirkpatrick-Baez mirror and multilayer zone plate. Opt. Express 21, 19311–19323 (2013).
Kang, H. et al. Focusing of hard X-rays to 16 nanometers with a multilayer Laue lens. Appl. Phys. Lett. 92, 221114 (2008).
Yan, H. et al. Two dimensional hard X-ray nanofocusing with crossed multilayer Laue lenses. Opt. Express 19, 15069–15076 (2011).
Nazaretski, E. et al. Performance and characterization of the prototype nm-scale spatial resolution scanning multilayer Laue lenses microscope. Rev. Sci. Instrum. 84, 033701 (2013).
Yan, H. et al. Quantitative X-ray phase imaging at the nanoscale by multilayer Laue lenses. Sci. Rep. 3, 1307 (2013).
Kang, H. et al. Oxidation of PtNi nanoparticles studied by a scanning X-ray fluorescence microscope with multilayer Laue lenses. Nanoscale 5, 7184–7187 (2013).
Rodenburg, J. et al. Hard-X-ray lensless imaging of extended objects. Phys. Rev. Lett. 98, 034801 (2007).
Thibault, P. et al. High-resolution scanning X-ray diffraction microscopy. Science 321, 379–382 (2008).
Kewish, C. et al. Reconstruction of an astigmatic hard X-ray beam and alignment of K-B mirrors from ptychographic coherent diffraction data. Opt. Express 18, 23420–23427 (2010).
Schropp, A. et al. Hard X-ray nanobeam characterization by coherent diffraction microscopy. Appl. Phys. Lett. 96, 091102 (2010).
Guizar-Sicairos, M. et al. One-dimensional hard X-ray field retrieval using a moveable structure. Opt. Express 18, 18374–18382 (2010).
Huang, X. et al. Quantitative X-ray wavefront measurements of fresnel zone plate and K-B mirrors using phase retrieval. Opt. Express 20, 24038–24048 (2012).
Schropp, A. et al. Full spatial characterization of a nanofocused X-ray free-electron laser beam by ptychographic imaging. Sci. Rep. 3, 1633 (2013).
Yan, H. & Chu, Y. Optimization of multilayer Laue lenses for a scanning X-ray microscope. J. Synchrotron Radiat. 20, 89–97 (2013).
Kang, H. et al. Nanometer linear focusing of hard x rays by a multilayer Laue lens. Phys. Rev. Lett. 96, 127401 (2006).
Conley, R. et al. Advanced multilayer Laue lens fabrication at NSLS-II. Proc. SPIE 8502, 850202 (2012).
Dierolf, M. et al. Ptychographic coherent diffractive imaging of weakly scattering specimens. New J. Phys. 12, 035017 (2010).
Bunk, O. et al. Influence of the overlap parameter on the convergence of the ptycho-graphical iterative engine. Ultramicroscopy 108, 481–487 (2008).
Born, M. & Wolf, E. Principles of Optics Seventh edition. 527–532 (Cambridge Univ. Press, 1999).
Yang, Y. et al. Coherent diffraction imaging of nanoscale strain evolution in a single crystal under high pressures. Nat. Commun. 4, 1680 (2013).
Jungjohann, K., Bliznakov, S., Sutter, P., Stach, E. & Sutter, E. In situ liquid cell electron microscopy of the solution growth of Au-Pd core-shell nanostructures. Nano Letters 13, 2964–2970 (2013).
Conley, R. et al. The NSLS-II multilayer Laue lens deposition system. Proc. SPIE 7448, 74480U (2009).
Acknowledgements
The authors acknowledge B. Mullany (BNL) for help with 3D modeling of the microscope and D. Kuhne (BNL) for machining/assembling of mechanical parts. We thank C. Kewish for fruitful discussion at the early stage of this project. Work at Brookhaven was supported by the Department of Energy, Office of Basic Energy Sciences under contract DE-AC-02-98CH10886. I.K.R. is supported by the ERC “nanosculpture” advanced grant 227711. The measurements were carried out at APS beamline 34-ID-C, built with US National Science Foundation grant DMR-9724294 and operated by the US Department of Energy, Office of Basic Energy Sciences, under contract no. DE-AC0206CH11357. The MLL post-growth processing was performed in part at the Center for Functional Nanomaterials, Brookhaven National Laboratory, supported by the U.S. Department of Energy, Office of Basic Energy Sciences, under Contract No. DE-AC02-98CH10886.
Author information
Authors and Affiliations
Contributions
Y.C. and H.Y. conceived the experiment. X.H., H.Y., L.L., D.L., R.H. and I.R. conducted the experiment. X.H., H.Y. and Y.C. analyzed the data. E.N., D.E., K.L. and X.H. designed and built the instrument. R.C., N.B. and J.Z. fabricated the MLL. All authors contributed to the writing of the manuscript.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Electronic supplementary material
Supplementary Information
Supplementary Information
Rights and permissions
This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivs 3.0 Unported License. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-nd/3.0/
About this article
Cite this article
Huang, X., Yan, H., Nazaretski, E. et al. 11 nm hard X-ray focus from a large-aperture multilayer Laue lens. Sci Rep 3, 3562 (2013). https://doi.org/10.1038/srep03562
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep03562
This article is cited by
-
Three-dimensional imaging of grain boundaries via quantitative fluorescence X-ray tomography analysis
Communications Materials (2022)
-
Hard X-ray focusing resolution and efficiency test with a thickness correction multilayer Laue lens
Nuclear Science and Techniques (2022)
-
The new X-ray/visible microscopy MAXWELL technique for fast three-dimensional nanoimaging with isotropic resolution
Scientific Reports (2022)
-
Multi-beam X-ray ptychography for high-throughput coherent diffraction imaging
Scientific Reports (2020)
-
A stacked prism lens concept for next-generation hard X-ray telescopes
Nature Astronomy (2019)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.