Abstract
Mechanical transducers based on nanowires promise revolutionary advances in biological sensing and force microscopy/spectroscopy. A crucial step is the development of simple and non-invasive techniques able to detect displacements with subpicometer sensitivity per unit bandwidth. Here, we design suspended tapered silicon nanowires supporting a range of optical resonances that confine and efficiently scatter light in the visible range. Then, we develop an optical method for efficiently coupling the evanescent field to the regular interference pattern generated by an incoming laser beam and the reflected beam from the substrate underneath the nanowire. This optomechanical coupling is here applied to measure the displacement of 50 nm wide nanowires with sensitivity on the verge of 1 fm/Hz1/2 at room temperature with a simple laser interferometry set-up. This method opens the door to the measurement of the Brownian motion of ultrashort nanowires for the detection of single biomolecular recognition events in liquids and single molecule spectroscopy in vacuum.
Similar content being viewed by others
Introduction
Nanowires grown by bottom-up techniques have high structural quality and their almost perfect axisymmetry makes the orthogonal vibration modes almost degenerate in frequency1. This genuine property of nanowires can be harnessed for mass and stiffness spectroscopy of molecular complexes1,2. In addition, nanowires inherently exhibit low force noise, which makes them ideal as nanoscale probes for biology research3, for pushing magnetic resonance force microscopy closer to achieving the goal of molecular imaging4,5 and for biological nanomechanical sensors2,6,7,8,9,10. The detection of the thermomechanical noise, also referred to as Brownian motion, dictated by the fluctuation-dissipation theorem11,12 is in many applications desirable in order to avoid modifying the resonator state13,14. The aforementioned applications thus, require non invasive displacement detection techniques with sub-picometer displacement sensitivities at room temperature. In addition, these techniques must keep the highest possible technical simplicity to be implemented in various forms of force microscopy and biosensing technologies able to operate in vacuum, air or liquids.
State of the art optical techniques with these requirements have achieved a detection limit near 10 fm/Hz1/2 in microcantilever transducers with highly reflective flat surfaces larger than the used wavelength15,16. When the width of the suspended beam is reduced to 200 nm, the displacement noise increases to 20–30 pm/Hz1/2, i.e. more than three orders of magnitude17. Higher signal degradation is expected in nanowires as a consequence of the small diameter and non flat surface that both lead to a significant reduction in the number of backscattered photons. Strikingly, recent reports have demonstrated that the vibration of certain nanowires can be detected with sensitivity of ~pm/Hz1/2 with interferometric1,18,19,20 and noninterferometric3 optical approaches. On one hand, this sensitivity enables to resolve the Brownian motion of long nanowires (typically 10 μm long), but it is clearly insufficient to detect shorter nanowires (length smaller than 2–3 μm) or higher vibration modes, that provide higher sensitivity in mass sensing and force gradient detection. On the other hand and more importantly, this sensitivity is not generally achieved in all nanowires and the cause for such inconsistency remains as an unanswered question. Moreover, little is known about the role of the nanowire size, polarization and wavelength in the optomechanical transduction.
In this work, we show experimental and theoretical data addressed to unveil the underlying mechanisms behind the light-nanowire interaction in an optical interferometry set-up. The results provide the optimal optical conditions and nanowire geometry to detect the Brownian fluctuations of semiconductor nanowires. Then, we discuss the open opportunities behind this discovery for ultrasensitive mass sensing as well as for detection of single biomolecular recognition events.
Results and discussion
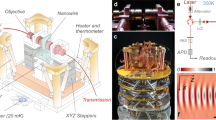
We have fabricated Si nanowires horizontally assembled and epitaxially clamped at the sidewalls of pre-patterned microtrenches on Si substrates by using the vapor-liquid-solid growth mechanism1,20 (Supplementary Section S1). The length of the nanowires ranges 8–16 μm and the diameter 40–240 nm. The vertical separation between the nanowire and the substrate underneath ranges 1.0–1.3 μm. A key feature in this study is that we chose growth conditions to produce tapered nanowires, in which the diameter linearly decreases from the clamped to the free end21. The vibration of the nanowires at room temperature was measured by using a homemade optical interferometer1 in a Fabry-Perot configuration operating at a wavelength of 633 nm (Supplementary Section S2). Fig. 1(a) shows a scanning electron microscopy (SEM) image of one of the fabricated tapered nanowires and, below, a frequency spectrum of the thermomechanical fluctuations that shows the quasidegeneration of the two orthogonal fundamental vibration modes1. The nanowire is 11.3 μm long and the diameter decreases from 150 ± 5 nm at the clamp to 60 ± 5 nm at the tip (determined by SEM). For the sake of simplicity, we hereinafter show the data for the mechanical fundamental submode with vibration direction closer to the substrate normal. When the tapered nanowire is visualized by dark-field microscopy, we observe colors ranging all over the visible spectrum between the clamped and free ends (Fig. 1(b), top)22,23,24. Since the dark-field is only sensitive to the scattered light, the colors of the collected light mainly arise from the light scattered by the nanowire. Our numerical simulations of the light-nanowire interaction show that silicon nanowires exhibit optical resonances that efficiently enhance the light scattering for certain values of the wavelength to diameter ratio (Supplementary Section S3). These resonances produce a correlation between the nanowire diameter and the color of the scattered light that fits with the dark-field data.
Mechanical and optical characterization of silicon nanowires.
(a) Scanning electron microscopy of a tapered nanowire (top), schematic of the optical displacement detection set-up (middle) and experimental frequency spectrum of the thermomechanical noise (bottom). The nanowire is 11.3 μm long and the diameter decreases from 150 ± 5 nm at the clamp to 60 ± 5 nm at the tip. The nanowire sample was placed in a vacuum chamber at approximately 10−6 torr and room temperature. The wavelength is 633 nm, the spot size 0.7 μm and the incident power 0.4 mW. Brownian fluctuation of the nanowire results in a measurable reflectivity fluctuation due to the interference between the light reflected off the nanowires and off the substrate. The displacement sensitivity is measured as a function of i) the laser beam position along the nanowire, x0, that is linearly related to the nanowire diameter due to the nanowire tapering, ii) laser polarization and iii) the separation between the nanowire and the substrate, h. The frequency spectrum shows the splitting of the fundamental mode in two close resonant peaks consisting on the nanowire vibrating in orthogonal directions as sketched in the inset. (b) Optical dark field image of the nanowire (top) and theoretical calculation of the scattering efficiency of the nanowire for a wavelength of 633 nm as a function of the diameter. The silicon nanowire exhibits colors ranging all over the visible spectrum. The theoretical simulations demonstrate that the dark-field color is correlated to the diameter. The numerical calculations of the scattering efficiency (with no substrate below the nanowire) show a series of optical resonances that strongly scatter the light for certain diameters that depend on the light polarization (bottom). The spatial distribution of the near electric-field intensity at these resonances (insets) shows the light confinement within the nanowire at these optical resonances. The resonance modes are denoted by two indexes, first index indicates the effective number of wavelength around the nanowire section and the second index the number of radial field maxima.
To obtain further insight on the nanowire optical resonances, we have calculated the scattering efficiency of the nanowire at a wavelength of 633 nm as a function of its diameter that we show at the bottom of Fig. 1B for transverse magnetic (TM) and transverse electric (TE) azimuthal polarizations. The spectra show a series of optical resonances where strong scattering of light takes place. The spatial distribution of the near electric-field intensity at these resonances (insets at bottom of Fig. 1(b)) shows the light confinement within the nanowire. The resonances arise from light trapped in circulating orbits by multiple internal reflections as it occurs in ‘whispering-gallery’ microresonators25. However, the small size of the nanowire makes that the electromagnetic field extends few nanometers out of the nanowire (evanescent field) and thus the resonances can efficiently interact with the surrounding electromagnetic field22. This property is essential to understand the presented sensitivity enhancement in the displacement detection of suspended nanowires. These modes are hereinafter referred to as leaky-mode resonances22,24.
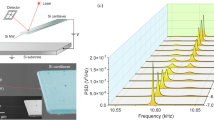
We now examine the role of the leaky-mode resonances in the optical detection of the mechanical displacement of nanowires. We measured the profiles of the reflectivity amplitude at the fundamental mechanical resonance of the nanowire for TM and TE polarizations (Fig. 2(a), circles). The profile of the nanowire oscillation amplitude (in spectral density units) calculated by combining finite element method (FEM) simulations and the fluctuation-dissipation theorem21 is also plotted (Fig. 2(a), line). The reflectivity amplitude due to the Brownian fluctuations exhibits maxima and minima. In other words, the reflectivity amplitude is not proportional to the vibration amplitude as it occurs in the linear regime of Fabry-Perot cavities. For TE polarization, a reflectivity amplitude maximum is located near the fixed end (x0 ≈ 2.5 μm), where the vibration amplitude is smaller. Notice that the nanowire cross-sectional area increases as the position approaches to the fixed end due to the nanowire tapering and thereby the vibration amplitude near the fixed end is significantly smaller than in nanowires with uniform cross-section.
Measuring the reflectivity fluctuations along a tapered nanowire.
(a) Experimental profiles of the reflectivity amplitude (symbols) at the fundamental mechanical resonance of the nanowire and vibration amplitude profile (line) calculated by the finite element method and the fluctuation-dissipation theorem. The reflectivity amplitude is non monotonic along the nanowire, exhibiting maxima and minima, indicating that the reflectivity and vibration amplitudes are not linearly correlated as it occurs in Fabry-Perot cavities. (b) Vibration amplitude versus the reflectivity amplitude for the nanowire region near the clamping (x0 < 2.5 μm). Displacement sensitivity on the verge of 1 fm/Hz1/2 is achieved. (c) Experimental reflectivity amplitude as a function of the angle between the electric field polarization vector and the nanowire axis for the laser beam positions, x0, marked in (a) as A, B and C.
In Fig. 2(b), we plot the vibration amplitude versus the reflectivity amplitude for the nanowire region near the clamping (x0 < 2.5 μm). Displacement sensitivity on the verge of 1 fm/Hz1/2 is achieved for our reflectivity noise, ≈10−7 (see discussion below). The obtained sensitivity is even one order of magnitude better than that obtained with state of the art interferometry on reflective flat surfaces with areas that largely exceed the wavelength15,16; and it is three orders of magnitude higher than the previously reported sensitivities in nanowires1,18,19. On the contrary, the nanowire is almost undetectable for TM polarization near the free end (at x0 ≈ 9 μm) where the vibration amplitude is higher. The displacement sensitivity strongly depends on the light polarization as shown in Fig. 2(c) for different laser beam positions along the nanowire. In all cases, the maximum light confinement is achieved at either, TM or TE polarizations. The displacement sensitivity when the laser beam is focused near the middle of the nanowire (position A) enhances for TM polarization. Conversely, the displacement sensitivity at the illumination position B closer to the free end, enhances for TE polarization. At position C, near the free end, the displacement sensitivity is almost insensitive to the light polarization.
We have calculated the displacement responsivity, defined as the ratio of the reflectivity variation to the nanowire displacement. Here, we calculate the displacement responsivity from the measurement of the reflectivity amplitude and the theoretical calculation of the vibration amplitude as described above. To investigate how the displacement responsivity depends on the nanowire diameter, we chose three nanowires separated from the substrate 1.050 ± 50 nm with different degrees of tapering that cover the diameter spectrum from 40 to 240 nm (Fig. 3, top graphs). Similar results are found with other nanowires. For a given polarization and wavelength, there are diameters at which the nanowire becomes ‘invisible’, i.e., the regular interference pattern produced by the incoming and reflected waves from the planar substrate is unaffected by the nanowire presence. Conversely, there are diameters, at which the responsivity is largely enhanced, i.e., the silicon nanowire significantly distorts the interference field. We have numerically solved the Maxwell's equations to calculate the field intensity collected in the far field by the objective lens used here (N.A. = 0.55) (Supplementary Section S4). The theoretical displacement responsivity for TM and TE polarizations closely resembles the experimental data (bottom graphs in Fig. 3). The comparison implies that the displacement sensitivity can largely be enhanced when optical resonances of the nanowire are excited. In the range of the diameters used in this study, we find the fundamental TM (0,1) mode for a diameter near 50 nm, TM (1,1) and TE (0,1) modes for a diameter near 120 nm and TM (2,1) and TE (1,1) modes for a diameter near 180 nm. The first index indicates the effective number of wavelengths around the nanowire section and the second index the number of radial field maxima22. Except for the fundamental TM (0,1) mode, the TM and TE modes are approximately degenerate.
Correlation between displacement responsivity and nanowire diameter.
Top graphs, Experimental displacement responsivity for TM and TE polarizations as a function of the nanowire diameter. The displacement responsivity is obtained by calculating the ratio of the experimental reflectivity amplitude to the theoretical vibration amplitude obtained from finite element method simulations and the fluctuation-dissipation theorem. The curves are obtained from data of three nanowires with different degrees of tapering separated from the substrate 1.050 ± 50 nm. Bottom graphs, Numerical calculations of the displacement responsivity by calculating the field intensity collected in the far field by an objective lens of N.A. = 0.55. The theoretical displacement closely resembles the experimental data shown in the graphs at the top.
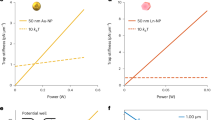
We now investigate the interaction of the ‘evanescent’ field of the optical resonance of the nanowire with the standing wave interference pattern. We choose, to investigate this effect, the narrowest nanowire able to support only the fundamental TM (0,1) mode (see Supplementary Section S5 higher modes). Advantageously, these nanowires show very strong polarization dependence that enables switching of the optomechanical coupling. In addition, the narrower the nanowire, the higher the sensitivity in force, stiffness and mass measurements. In the absence of a substrate underneath, the laser beam (wavelength of 633 nm) is resonantly scattered at the TM (0,1) mode for a diameter of about 40 nm (Fig. 4(a), top). The interaction of TM (0,1) mode with the surrounding electromagnetic interference field produces a large redshift of this mode, resulting in a displacement of the TM (0,1) mode to diameters around 50 nm for the working wavelength. Fig. 4(a) shows the evolution of the displacement responsivity for diameters around 50 nm and the near electric-field intensity distribution with the separation between the nanowire and the substrate. The TM (0,1) peak distorts and shifts with the distance to the substrate, which suggests that the nanowire is subject to significant optomechanical coupling. To quantify the optomechanical coupling, we have calculated the figure of merit for cavity optomechanical systems given by  , where ωc is the optical resonance frequency (ωc) corresponding to the TM (0,1) mode and D is the nanowire-substrate separation26. Fig. 4(b) shows a color-intensity map of the scattering efficiency as a function of the optical frequency and the separation. As the separation decreases, the TM (0,1) mode linearly shifts to higher frequencies. The linear fitting of the optical resonance frequency versus the separation provides a optomechanical coupling constant gOM ≅ 423 GHz/nm, which is close to the highest value achieved so far27, but with a mechanical transducer more than three orders of magnitude lighter. We have found that the gOM decreases with the nanowire diameter, which suggests that the extraordinary optomechanical coupling arises from the evanescent field owing to the small size of the nanowire that makes that the nanowire acts an effective antenna that efficiently interacts with the regular interference pattern.
, where ωc is the optical resonance frequency (ωc) corresponding to the TM (0,1) mode and D is the nanowire-substrate separation26. Fig. 4(b) shows a color-intensity map of the scattering efficiency as a function of the optical frequency and the separation. As the separation decreases, the TM (0,1) mode linearly shifts to higher frequencies. The linear fitting of the optical resonance frequency versus the separation provides a optomechanical coupling constant gOM ≅ 423 GHz/nm, which is close to the highest value achieved so far27, but with a mechanical transducer more than three orders of magnitude lighter. We have found that the gOM decreases with the nanowire diameter, which suggests that the extraordinary optomechanical coupling arises from the evanescent field owing to the small size of the nanowire that makes that the nanowire acts an effective antenna that efficiently interacts with the regular interference pattern.
Simulation of the optomechanical coupling in a 50 nm wide silicon nanowire.
(a) Evolution with the nanowire-substrate separation (D) of the displacement responsivity versus the diameter and the near electric-field intensity distribution for a diameter of 50 nm. This is the lowest diameter at which the nanowire is able to support the fundamental TM (0,1) mode. The interaction of the ‘evanescent’ field of the optical resonance with the surrounding standing wave interference pattern produces a significant redshift of the optical resonance. This results into an increase of the resonant diameter from 40 nm to 50–60 nm that is indicative of an unprecedented optomechanical coupling. The displacement responsivity is maximal when the nanowire is placed midway between nodes and anti-nodes of the standing wave intensity field, i.e. maximum slope regions (separation of 1025 nm); being minimal at the anti-nodes (separation of 950 nm). (b) Top: color intensity map of the scattering efficiency for the fundamental TM (0,1) mode as a function of the optical frequency and the nanowire-substrate separation (D). Bottom: nanocavity optical resonance frequency versus the mechanical displacement (symbols). The optomechanical coupling coefficient obtained from the slope of the linear fit (line) is 423 GHz/nm.
The attainable displacement detection limit in our experimental set-up is determined by the optical noise in the photodetector15,16,17 and the displacement responsivity. The main sources of optical noise are the shot noise and the Johnson noise originated from the intensity-voltage conversion. Shot noise dominates for the laser power used in our experiments, ≈400 μW. Our theoretical detection limit in reflectivity is of about 10−7, which is in good agreement with the experimentally measured values. An optimal displacement responsivity of 1.8 × 10−5 pm−1 can be obtained for a nanowire with diameter of 50 nm at a wavelength of 633 nm by positioning the nanowire in the region of highest intensity gradient of the interference field (see Fig. 4(a)). Notice that for other leaky modes, the optimal position may vary depending on the near electric field distribution (Supplementary Section S5). For the values of laser power used here, our detection limit is of about 5 fm/Hz1/2. This value provides enough room to detect shorter nanowires that exhibit higher resonance frequencies and smaller masses. This directly results in higher sensitivity in mass sensing or force gradient detection. In Fig. 5(a) we plot the theoretical thermal amplitude at resonance as a function of the nanowire length in vacuum1,5,19 (quality factor ≈ 3000) and in aqueous solution3 (quality factor ≈ 3). The optical detection paradigm demonstrated here would enable the measurement of the Brownian fluctuations at resonance of nanowires with lengths of ≈200 nm and 700 nm in vacuum and liquid, respectively. The mass sensitivity in vacuum without excitation would be of few hundreds of yoctogram and near one yoctogram with external excitation (Fig. 5(b)). This outstanding sensitivity can potentially be applied for obtaining new insights into diffusion of atoms and molecules along nanowires as well as for chemical identification of molecules and proteins7,28. Aqueous solutions are the natural environment where biological molecules adopt their native structure and interact with other molecules to perform complex functions in cells. Also, optical detection is best suited for liquid environments. The viscous damping highly reduces the quality factor, but this price is cheap compared with the fascinating applications that tiny nanowires can find in bionsensing and intracellular sensing. Few hundreds of zeptograms can be detected with short nanowires in liquid. This sensitivity would enable the detection of single ligand-receptor events. In addition, nanowires can safely penetrate the plasma membrane and enter biological cells for drug and gene delivery, electrophysiology and endoscopy29,30,31. We envision that our findings will also place at reach intracellular sensing based on nanowires.
Detection limits of a mass sensor based on a 50 nm wide nanowire.
(a) Theoretical thermal amplitude at resonance and (b) mass detection limit with no external excitation as a function of the nanowire length for quality factors of 3000 (that mimics the vacuum situation) and 3 (that mimics the situation when the nanowire is in liquid). The theoretical displacement detection limit is of about 5 fm/Hz1/2 for laser powers of ≈400 μW that enable the measurement of the thermal fluctuations at resonance of nanowires with lengths of ≈200 nm and 700 nm in vacuum and liquid, respectively. The resulting mass sensitivity for these nanowires is ~100 yoctograms in vacuum and ~100 zeptograms in liquids.
Conclusions
Extraordinary mechanical, optical and electrical properties of silicon nanowires have been exploited in a wide variety of applications including nanoelectronics, photonics, nanomedicine and green energy. Here, we find that the excellent optical and mechanical properties merge when the optical resonances that confine the light within the nanowire couple to the nanowire displacement in a Fabry-Perot nanocavity configuration. The ever-increasing control over nanostructure dimensions can now be used to engineer desired optomechanical devices with nanowires for specific applications. In particular, the optomechanical coupling can be tailored to follow Brownian fluctuations of tiny nanowires with masses in the femtogram range, thus opening fascinating applications for biological sensing with unprecedented sensitivity and for obtaining new insights on surface science at the level of single molecules. The excellent optomechanical coupling can also be harnessed in high finesse optical cavities for achieving quantum ground state27, or for self-sustained oscillation with high frequency stability20. However, as nanotechnology has taught us in the last decade in other discoveries, the opportunities opened when different disciplines meet at the nanoscale, as here with optics and mechanics, are simply beyond our imagination.
Methods
Device fabrication
Silicon on insulator (SOI) substrates with a <110> orientation of the 2-μm-thick device layer were patterned by photolithography and reactive ion etching to define the simple supporting microstructures with <111> oriented sidewalls on which the nanowires were intended to grow. Before nanowire growth, the substrates were coated with 80- or 150-nm-diameter gold nanoparticles (British Biocell). Silicon nanowires were grown in an atmospheric-pressure chemical vapour deposition (CVD) reactor at 800°C with 10% H2/Ar as both diluent and carrier gas. Flow rates of 270 and 45 s.c.c.m. were used, respectively. The carrier gas was passed through a liquid SiCl4 bubbler maintained at 0°C to maintain a constant vapor pressure.
Experimental setup
The silicon die was mounted on a three-axis piezoelectric translation stage for positioning and scanning under the probe beam. The sample on the piezoelectric translation stage was placed into a small vacuum chamber pumped down to the 1 × 10−6 torr. A 5-mW He–Ne gas laser beam (λ = 633 nm) was focused onto the sample through an intensity filter, beamsplitter and a ×50 objective with a numerical aperture of 0.55. The spot size was 0.7–1.5 microns. The optical power of the beam incident on the nanowires was of about 0.5 mW. The reflected light was collected by the objective and detected by a photovoltaic silicon pin diode followed by a low-noise current-to-voltage preamplifier and high-speed digitizer connected to a PC.
References
Gil-Santos, E. et al. Nanomechanical mass sensing and stiffness spectrometry based on two-dimensional vibrations of resonant nanowires. Nat. Nanotechnol. 5, 641–645 (2010).
Tamayo, J., Kosaka, P. M., Ruz, J. J., San Paulo, Á. & Calleja, M. Biosensors based on nanomechanical systems. Chem. Soc. Rev. 42, 1287–1311 (2013).
Sanii, B. & Ashby, P. D. High sensitivity deflection detection of nanowires. Phys. Rev. Lett. 104, 147203 (2010).
Degen, C., Poggio, M., Mamin, H., Rettner, C. & Rugar, D. Nanoscale magnetic resonance imaging. Proc. Natl. Acad. Sci. 106, 1313–1317 (2009).
Nichol, J. M., Hemesath, E. R., Lauhon, L. J. & Budakian, R. Nanomechanical detection of nuclear magnetic resonance using a silicon nanowire oscillator. Phys. Rev. B 85, 054414 (2012).
Arlett, J., Myers, E. & Roukes, M. Comparative advantages of mechanical biosensors. Nat. Nanotechnol. 6, 203–215 (2011).
Hanay, M. et al. Single-protein nanomechanical mass spectrometry in real time. Nat. Nanotechnol. 7, 602–608 (2012).
Waggoner, P. S. & Craighead, H. G. Micro-and nanomechanical sensors for environmental, chemical and biological detection. Lab Chip 7, 1238–1255 (2007).
Boisen, A. & Thundat, T. Design & fabrication of cantilever array biosensors. Mater. Today 12, 32–38 (2009).
Feng, X., He, R., Yang, P. & Roukes, M. Very high frequency silicon nanowire electromechanical resonators. Nano Lett. 7, 1953–1959 (2007).
Tamayo, J., Calleja, M., Ramos, D. & Mertens, J. Underlying mechanisms of the self-sustained oscillation of a nanomechanical stochastic resonator in a liquid. Phys. Rev. B 76, 180201 (2007).
Cleland, A. & Roukes, M. Noise processes in nanomechanical resonators. J. Appl. Phys. 92, 2758–2769 (2002).
Gil-Santos, E. et al. Mass sensing based on deterministic and stochastic responses of elastically coupled nanocantilevers. Nano Lett. 9, 4122–4127 (2009).
Gavartin, E., Verlot, P. & Kippenberg, T. A hybrid on-chip optomechanical transducer for ultrasensitive force measurements. Nat. Nanotechnol. 7, 509–514 (2012).
Rugar, D., Mamin, H. J., Erlandsson, R., Stern, J. E. & Terris, B. D. Force microscope using a fiber-optic displacement sensor. Rev. Sci. Instrum. 59, 2337–2340 (1988).
Schonenberger, C. & Alvarado, S. F. A differential interferometer for force microscopy. Rev. Sci. Instrum. 60, 3131–3134 (1989).
Kouh, T., Karabacak, D., Kim, D. & Ekinci, K. Diffraction effects in optical interferometric displacement detection in nanoelectromechanical systems. Appl. Phys. Lett. 86, 013106 (2005).
Nichol, J. M., Hemesath, E. R., Lauhon, L. J. & Budakian, R. Displacement detection of silicon nanowires by polarization-enhanced fiber-optic interferometry. Appl. Phys. Lett. 93, 193110 (2008).
Belov, M. et al. Mechanical resonance of clamped silicon nanowires measured by optical interferometry. J. Appl. Phys. 103, 074304 (2008).
Ramos, D. et al. Optomechanics with Silicon Nanowires by Harnessing Confined Electromagnetic Modes. Nano Lett. 12, 932–937 (2012).
Malvar, O. et al. Tapered silicon nanowires for enhanced nanomechanical sensing. Appl. Phys. Lett. 103, 033101 (2013).
Cao, L. et al. Engineering light absorption in semiconductor nanowire devices. Nature Mater. 8, 643–647 (2009).
Brönstrup, G. et al. Optical properties of individual silicon nanowires for photonic devices. ACS Nano 4, 7113–7122 (2010).
Seo, K. et al. Multicolored vertical silicon nanowires. Nano Lett. 11, 1851 (2011).
Braginsky, V., Gorodetsky, M. & Ilchenko, V. Quality-factor and nonlinear properties of optical whispering-gallery modes. Phys. Lett. A 137, 393–397 (1989).
Favero, I. & Karrai, K. Optomechanics of deformable optical cavities. Nature Photon. 3, 201–205 (2009).
Eichenfield, M., Camacho, R., Chan, J., Vahala, K. J. & Painter, O. A picogram-and nanometre-scale photonic-crystal optomechanical cavity. Nature 459, 550–555 (2009).
Chaste, J. et al. A nanomechanical mass sensor with yoctogram resolution. Nat. Nanotechnol. 7, 301–304 (2012).
Xu, L. et al. Design and Synthesis of Diverse Functional Kinked Nanowire Structures for Nanoelectronic Bioprobes. Nano Lett. 13, 746–751 (2013).
Shalek, A. K. et al. Vertical silicon nanowires as a universal platform for delivering biomolecules into living cells. Proc. Natl. Acad. Sci. 107, 1870–1875 (2010).
Yan, R. et al. Nanowire-based single-cell endoscopy. Nat. Nanotechnol. 7, 191–196 (2012).
Acknowledgements
We acknowledge financial support from the Spanish Science Ministry (MINECO) through projects TEC2011-29120-C05-04; and from European Research Council through Starting Grant NANOFORCELLS (ERC-StG-2011-278860). D.R. acknowledges financial support from the EU grant Marie Curie IOF-2009-254996.
Author information
Authors and Affiliations
Contributions
D.R., E.G., M.C., A.S. and J.T. conceived and designed the experiments. A.S. fabricated the devices. D.R. and E.G. performed the interferometry experiments. O.M. performed the electron microscopy characterization of the tapered nanowires. O.M. & D.R. carried out the dark field images of nanowires. D.R., J.M.L. & V.P. carried out modeling and simulations. J.T. wrote this manuscript with inputs from all authors. All authors analyzed the data, discussed the results and commented on the manuscript.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Electronic supplementary material
Supplementary Information
Silicon nanowires: where mechanics and optics meet at the nanoscale
Rights and permissions
This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivs 3.0 Unported License. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-nd/3.0/
About this article
Cite this article
Ramos, D., Gil-Santos, E., Malvar, O. et al. Silicon nanowires: where mechanics and optics meet at the nanoscale. Sci Rep 3, 3445 (2013). https://doi.org/10.1038/srep03445
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep03445
This article is cited by
-
Gunn-Hilsum Effect in Mechanically Strained Silicon Nanowires: Tunable Negative Differential Resistance
Scientific Reports (2018)
-
Effect of water-DNA interactions on elastic properties of DNA self-assembled monolayers
Scientific Reports (2017)
-
Recent Advances in Silicon Nanowire Biosensors: Synthesis Methods, Properties, and Applications
Nanoscale Research Letters (2016)
-
Mass and stiffness spectrometry of nanoparticles and whole intact bacteria by multimode nanomechanical resonators
Nature Communications (2016)
-
High-sensitivity linear piezoresistive transduction for nanomechanical beam resonators
Nature Communications (2014)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.