Abstract
We investigate the Lorentz-covariant deformed algebra for Dirac oscillator problem, which is a generalization of Kempf deformed algebra in 3 + 1 dimension of space-time, where Lorentz symmetry are preserved. The energy spectrum of the system is analyzed by taking advantage of the corresponding wave functions with explicit spin state. We obtained entirely new results from our development based on Kempf algebra in comparison to the studies carried out with the non-Lorentz-covariant deformed one. A novel result of this research is that the quantized relativistic energy of the system in the presence of minimal length cannot grow indefinitely as quantum number n increases, but converges to a finite value,  where c is the speed of light and β is a parameter that determines the scale of noncommutativity in space. If we consider the fact that the energy levels of ordinary oscillator is equally spaced, which leads to monotonic growth of quantized energy with the increment of n, this result is very interesting. The physical meaning of this consequence is discussed in detail.
where c is the speed of light and β is a parameter that determines the scale of noncommutativity in space. If we consider the fact that the energy levels of ordinary oscillator is equally spaced, which leads to monotonic growth of quantized energy with the increment of n, this result is very interesting. The physical meaning of this consequence is discussed in detail.
Similar content being viewed by others
Introduction
Large momenta tied to large spatial dimensions, that appears in string theoretic considerations, may shed light to the existence of a minimal length scale. The coordinates in D-dimensional space no longer commutable with one another under the presence of minimal length scale. The interest for studying the effects of noncommutativity on characteristics of quantum systems has been gradually increasing over the past decade. Several works in this direction suggest the existence of natural ultra violet (UV) cut-off at the planck scale. This reflects the existence of non-zero uncertainties in position and/or in momentum, giving the concept of the generalized uncertainty principal (GUP) that involves some correction terms in its expression. Of course, the consideration of GUP in a certain quantum system leads to a modification of both wave functions and the corresponding energy spectrum1,2,3,4.
Perturbative string theory in sufficiently high energy regime such as black hole may give rise to disturbance of space-time implying the appearance of non-negligible effects of the minimal length5. The consideration of minimal length concept is crucial for precise description of broad physical fields such as non-commutative geometry6, non-commutative field theories7,8,9, black hole physics10,11, loop quantum gravity12, string theory13,14,15,16,17 and others18,19,20,21. For nonrelativistic case, the solution of Schrödinger equation in momentum space and the corresponding energy spectrum has been studied in arbitrary dimensions considering minimal length, mainly for basic systems involving harmonic oscillator19,20,22, coulomb potential system23,24,25,26 and one-dimensional box problems27. By the way, the only relativistic problem that can be solved without approximation is Dirac oscillator (DO) established via the substitution P → P − iβmωX in relativistic Dirac equation28. Dirac oscillator has attracted great attention thanks to its essential applicability in particle physics and quantum gravity.
Dirac oscillator has been investigated in momentum space representation by Green's function technique29,30 and by coherent states approach31. It turned out that Kempf algebra32 is useful for determining wave functions and energy spectrum in 1D with consideration of its thermodynamic properties in the presence of minimal length. This approach has been extended to 3D by Quesne and Tkachuk33 using supersymmetric quantum mechanics based on shape-invariance methods.
In this work, we plan to solve the DO problem in a somewhat different context, suggesting a new covariant deformed algebra in 3 + 1 space-time, which preserves Lorentz symmetry. Due to several difference of our research from Kempf's one based on his deformed algebra, our result is somewhat different and cannot be reduced to a simple one in nonrelativistic limit. In particular, we are interested in investigating the effects of space deformation, characterized by the presence of minimal length scale, on quantized energy spectrum for a relativistic Dirac oscillator. The behavior of energy spectrum in high quantum number limit (n → ∞) will be analyzed in order to promote deep understanding for intrinsic quantum nature of the system.
We introduce the Lorentz covariant deformed algebra and it will be used to solve the quantum problem of Dirac oscillator with minimal length in momentum representation. Dirac wave functions will be derived and the DO energy spectrum will be determined. Its asymptotic behavior will be estimated in both non-relativistic and non-deformed cases. An interesting discrepancy between our energy spectrum and the one obtained by Kempf deformed algebra34 will be addressed.
Results
Let us start with a brief review of deformed quantum mechanics in 3 dimensions. According to Refs. 22, 33, we introduce deformed formula of position and momentum operators represented in terms of momentum variable such that


where β, β′ and γ are some non-negative parameters which are very small. These operators yield non-covariant Kempf algebra that reads to



This algebra with the parameters β = γ = 0 in 3D is initiated by Snyder35 in 1940's. After on, the attempt for investigating Dirac oscillator with this algebraic formulation was realized by Quesne et al.36,37 in 1 + 1 dimensions in the case β′ = γ = 0. They derived wave functions of the system and estimated the bound-state energy.
The components of the angular momentum are given by

These satisfy the usual commutation relations of the form

If we consider physical states with 〈P〉 = 0 and the fact that the momentum uncertainties ΔPi are isotropic, canonical variables represented in Eqs. (1) and (2) no longer gives the Heisenberg uncertainty principle. Instead, we can express its modified form (GUP) as

By taking the saturation of GUP and minimizing it with respect to ΔPi, we have an isotropic minimal length which is

The parameter γ in Eq. (1) does not affect the commutation relations and only modify the squeezing factor of the momentum space measure. In fact, the inner product is now defined by

Now, let us introduce the (3 + 1) dimensional Lorentz-covariant algebra33,34. In this case we have to make the following substitution in Eqs. (3)–(5):  , pixi → p0x0 − pixi = pνxν, where pν = (p0, pi) and xν = (x0, xi). If we consider in this scheme that
, pixi → p0x0 − pixi = pνxν, where pν = (p0, pi) and xν = (x0, xi). If we consider in this scheme that

we easily show that the Lorentz covariant commutation relations can be deduced to be



where gμν = Diag(1, −1, −1, −1) and

Notice that this algebra collapses to the Snyder's algebra35 for D = 3, β = γ = 0 and β′ = (a/ℏ)2. Some algebras that can be fulfilled with Lμν are given by



Finally the inner product in momentum space, Eq. (10), becomes

The Dirac equation in (3 + 1) dimensions for a free spinor reads (γμpμ − m) ψ = 0, where m is the rest mass of the particle and ψ is the four component spinor wave function and γμ are four square matrices. In general, the standard representation of γμ has the form

where σ is (2 × 2) hermitian Pauli matrix and I is the (2 × 2) unit matrix. The relativistic Dirac oscillator introduced by other researchers28 can now be obtained using the non-minimal coupling P − imωX in the free particle Dirac equation, where ω is the frequency of the oscillator. This coupling gives

From the substitution of  in Eq. (21), we obtain the following coupled differential equations
in Eq. (21), we obtain the following coupled differential equations


Because ψb(p, p0) approaches zero as the system become nonrelativistic case ( ), ψb(p, p0) is usually called the small wave function38. However, ψa(p, p0) is relatively large in most cases so that we can call it as the large wave function. Let us rearrange Eq. (23) in terms of ψb. Then, by inserting it in Eq. (22), we obtain the operator equation for the large component such that
), ψb(p, p0) is usually called the small wave function38. However, ψa(p, p0) is relatively large in most cases so that we can call it as the large wave function. Let us rearrange Eq. (23) in terms of ψb. Then, by inserting it in Eq. (22), we obtain the operator equation for the large component such that

Wave functions
At this stage, let us decompose the wave function into a radial part and spin angular part as

where  is a unit vector.
is a unit vector.
For the case of a simple situation β′ = γ = 0, the use of the algebra of Eq. (12) leads to


where α = 2β(1 − β)((p0)2 − p2) and L is the orbital angular momentum. Now we consider the action of σL on the spin-angular function  :
:

Here, the quantum number κ is equal to s(2j + 1) − 1 where s is the spin, j = l + s and l is the angular momentum. Then, using the first of Eq. (25) with Eqs. (26)–(28), Eq. (24) becomes

Here, we used the relation W = cp0. If we consider Eq. (11), the momentum space representation of X2 is given by

From the use of this relation in Eq. (29), we obtain the following differential equation

To simplify this equation, we define a new deformation parameter of the form

This allows us to rewrite Eq. (31) as

Introducing new variables such that

we cast Eq. (33) in the form

where

Let us make further change of variables,  and
and  , along with
, along with

where λc is a constant that will be determined later. Then, we have

At this stage we eliminate the term proportional to  by choosing λc to be the solution of the following differential equation
by choosing λc to be the solution of the following differential equation

Through a straightforward calculation, we easily have

Among these two solutions, the physically acceptable one is only λc,+. This can be verified by examining them with reference of the GUP using the same method given in Ref. 34 for a similar problem.
A further simplification can be fulfilled by eliminating the centrifugal barrier term in Eq. (38) by setting f (S) = Slg (S) and z = 2S2 − 1:

We now introduce the following new parameters

where n′ is non-negative integer. Then, by imposing the following constraint

we can rewrite Eq. (41) in the form

We see that the solutions of this equation are expressed in terms of Jacobi polynomials

where N is a normalization constant. Then, the large radial component F (z) is given by

By returning to the old variable p, we immediately have

We now calculate the small component of the DO wave function ψb (p, p0) using

Using the Lorentz-covariant operator algebra (see Methods section), we confirm that this equation yields

where  .
.
It is important to use the action of σL and σp on  function, where
function, where

and after some simplifications on ψb (p,p0) formula, we can express the small radial wave function G (p, p0) as

Notice that this is equivalent to the one that appears in Kempf non-covariant deformed algebra34. By using ω′ instead of ω, where

Eq. (51) can be rewritten as

This change makes it easy to normalize the wave function of the relativistic Dirac oscillator on large and small radial components:


The large radial component R1(p, p0) is given by

where f (p) is defined as f (p) = 1 + θp2.
For the case of the small component R2 (p, p0), it is necessary to distinguish spin up and spin down states. For  , we have
, we have

whereas, for  , it yields
, it yields

When we derive these two equations, some properties relevant to the Jacobi polynomials, which have appeared in Ref. 39, are used.
Now, let us determine the normalization constant N via the relation

If we consider this, the normalized components of the wave function F (p,p0) and G (p,p0) deduced from Eqs. (54) and (55) become


where

with

Energy spectrum
Using the expressions of n′, a, b, λc,+ and ζ given in Eq. (43), it is possible to find the energy spectrum of Dirac oscillator with Lorentz-covariant deformed algebra. A straightforward calculation leads to.

where we have set

It is interesting to link Eq. (64) with the energy spectrum of 3D Dirac oscillator obtained with the non-covariant Kempf deformed algebra34. In fact, by inspection, we easily see that Eq. (64) can be rewritten as

where Wnc is the energy spectrum of Dirac oscillator developed with non-covariant deformed algebra34:

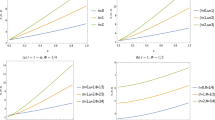
From Fig. 1, we see that Wc is lower than Wnc except when β = 0. The difference between them becomes large as quantum number n and parameter β increase.
The presence of the additional factor (1 + ℏωmβΔ)−1 makes the energy spectrum bounded. In fact, by considering  , we obtain
, we obtain

Thus, the energy of the relativistic Dirac oscillator in deformed space is not allowed to increase indefinitely, but approaches to a finite value. This is the main result of our report. However, if we remove the deformation of the space by setting β→0, the energy in the large n limit becomes  , as expected. In more detail, in order to get increasing values of the energy without upper bound when n increases, we see from Eq. (64) that a necessary condition is
, as expected. In more detail, in order to get increasing values of the energy without upper bound when n increases, we see from Eq. (64) that a necessary condition is  , yielding the following constraint
, yielding the following constraint

It is shown in second part of Methods section that how to map the solution of Dirac oscillator with Lorentz-covariant deformed algebra to the solution with the non-covariant deformed algebra of Kempf et al.1,2,3,4 through (alternative) derivation of the energy spectrum. Now, let's analyze the results in some limiting cases.
-
i
The case β = 0
In this case we have Wc = Wnc and one obtains
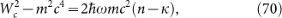
or
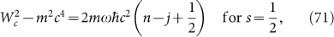
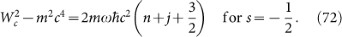
These are exactly the energy levels of the usual Dirac oscillator.
-
ii
The non-relativistic limit
The non-relativistic limit is obtained by setting Wc = mc2 + Ec with the assumption that
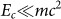 , where Ec being the non-relativistic energy. Indeed, from Eq. (66), we obtain the following formula
, where Ec being the non-relativistic energy. Indeed, from Eq. (66), we obtain the following formula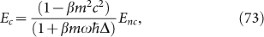
where Enc is the non-relativistic energy of the system analyzed with non-covariant algebra. This relation shows that the non-covariant deformed algebra does not equivalent to the non-relativistic limit of the Lorentz-covariant deformed algebra. This conclusion coincide with the previous reports36,37 developed for the case of the one-dimensional Dirac oscillator with Lorentz covariant deformed algebra. We see from Eq. (73) that the non-bound condition, Eq. (69), also holds for the non-relativistic case.
Before closing this section, let us see the allowed condition associated with the parameter θ. By rewriting Eq. (32) as a function of θ, we have

Using Eq. (69) one easily get the following bound condition for the norm of 3D momentum

Using again Eq. (69) we further obtain

which means that an UV cut-off naturally implemented in the Lorentz-covariant deformed algebra. By combining Eqs. (75) and (76), one obtains the condition

for the physically acceptable states. This can also be obtained from the deformed inner product, by demanding that the weight function in Eq. (19) is free from singularities36,37.
Discussion
In this paper, we have investigated the problem of relativistic Dirac oscillator with minimal length in 3 + 1 dimensional space-time on the basis of Lorentz-covariant algebra introduced using particular variable transformations (in the case β′ = γ = 0). The wave functions of the system and the corresponding energy spectrum are derived considering the Lorentz covariant commutation relations given in Eqs. (12)–(14). We confirmed that the energy spectrum is different from the one obtained from Kempf non-covariant algebra34 by the presence of the factor (1 + βmωℏΔ)−1 [see Eq. (66)], which proves the novelty of the algebra used.
It was important to remark that the energy spectrum we obtained is bounded as shown in Eq. (68) whereas the energy spectrum for the DO problem based on the Kempf algebra is not. If we compare this with the familiar result that the energy levels of the ordinary oscillator is equally spaced leading monotonic growth of the energy with the increment of the quantum number n40, this result is very surprising. Apparently, Eq. (68) implies that the spacing of the energy levels asymptotically approaches to zero for sufficiently large n. We can conclude that the deformation of space restricts the total (relativistic) quantum energy for a mode and the allowed energy become small with the increase of deformation factor β. In the meantime, in case that the deformation of the space disappears, this effect vanishes and the energy spectrum recovers to previously known one as expected.
We have found that Kempf deformed algebra is not a non-relativistic limit of Lorentz-covariant deformed algebra. This outcome is in good agreement with the discussions in Refs. 36, 37. In the limit β → 0, the usual relativistic DO eigenvalues are recovered. The two components of wave function take the form of DO wave functions with Kempf algebra in 3 dimensions33,34, but the normalization constant and the quantities a and b are dependent on p0 which manifest themselves in the small parameter θ.
Methods
Lorentz-covariant operator algebra
To manage Eq. (48) in the text, it is useful to consider some relations of Ref. 33 with appropriate modifications considering the Lorentz-covariant algebra, which are



where  .
.
Derivation of the energy spectrum
We show how to map the solution of Dirac oscillator with Lorentz-covariant deformed algebra to the solution with the non-covariant deformed algebra of Kempf et al.1,2,3,4. The key quantities are kc and ζc and the corresponding ones in the case of the non-covariant deformed algebra are given by34


It is easy to show that



Now, by comparing Eqs. (81) and (82) with Eqs. (83) and (84) and using Eq. (43), we obtain

which is exactly the same as Eq. (66). On the other hand the wave functions given in Eqs. (60) and (61) can be obtained from the ones obtained in the setup with non-covariant deformed algebra by using Eq. (32) and  and taking into account an extra factor (θ/β)3/2 in the normalization constant.
and taking into account an extra factor (θ/β)3/2 in the normalization constant.
References
Kempf, A. Uncertainty relation in quantum mechanics with quantum group symmetry. J. Math. Phys. 35, 4483–4496 (1994).
Kempf, A., Mangano, G. & Mann, R. B. Hilbert space representation of the minimal length uncertainty relation. Phys. Rev. D 52, 1108–1118 (1995).
Kempf, A. Non-pointlike particles in harmonic oscillators. J. Phys. A: Math. Gen. 30, 2093–2102 (1997).
Hinrichsen, H. & Kempf, A. Maximal localization in the presence of minimal uncertainties in positions and in momenta. J. Math. Phys. 37, 2121–2137 (1996).
Gross, D. J. & Mende, P. F. String theory beyond the Planck scale. Nucl. Phys. B 303, 407–454 (1988).
Capozziello, S., Lambiase, G. & Scarpetta, G. Generalized uncertainty principle from quantum geometry. Int. J. Theor. Phys. 39, 15–22 (2000).
Douglas, M. R. & Nekrasov, N. A. Noncommutative field theory. Rev. Mod. Phys. 73, 977–1029 (2001).
Minwalla, S., Van Raamsdonk, M. & Seiberg, N. Noncommutative perturbative dynamics. J. High Energy Phys. JHEP02, 020(1–30) (2000).
Szabo, R. J. Quantum field theory on noncommutative spaces. Phys. Rep. 378, 207–299 (2003).
Scardigli, F. Generalized uncertainty principle in quantum gravity from micro-black hole gedanken experiment. Phys. Lett. B 452, 39–44 (1999).
Scardigli, F. & Casadio, R. Generalized uncertainty principle, extra dimensions and holography. Class. Quant. Grav. 20, 3915–3926 (2003).
Garay, L. J. Quantum gravity and minimal length. Int. J. Mod. Phys. A 10, 145–166 (1995).
Veneziano, G. A stringy nature needs just two constants. Europhys. Lett. 2, 199–204 (1986).
Amati, D., Ciafaloni, M. & Veneziano, G. On BRST quantization of second class constraint algebras. Phys. Lett. B 213, 41–47 (1989).
Konoshi, K., Paffuti, G. & Provero, P. Minimum physical length and the generalized uncertainty principle in string theory. Phys. Lett. B 234, 276–284 (1990).
Kato, M. Particle theories with minimum observable length and open string theory. Phys. Lett. B 245, 43–47 (1990).
Guida, R., Konishi, K. & Provero, P. On the short distance behavior of string theories. Mod. Phys. Lett. A 6, 1487–1504 (1991).
Hossenfelder, S. The minimal length and large extra dimensions. Mod. Phys. Lett. A 19, 2727–2744 (2004).
Hossenfelder, S. Running coupling with minimal length. Phys. Rev. D 70, 105003(1–11) (2004).
Hossenfelder, S. Suppressed black hole production from minimal length. Phys. Lett. B 598, 92–98 (2004).
Sastry, R. R. Quantum mechanics of smeared particles. J. Phys. A: Math. Gen. 33, 8305–8318 (2000).
Chang, L. N., Minic, D., Okamura, N. & Takeuchi, T. Exact solution of the harmonic oscillator in arbitrary dimensions with minimal length uncertainty relations. Phys. Rev. D 65, 125027(1–8) (2002).
Fityo, T. V., Vakarchuk, I. O. & Tkachuk, V. M. One-dimensional Coulomb-like problem in deformed space with minimal length. J. Phys. A: Math. Gen. 39, 2143–2150 (2006).
Brau, F. Minimal length uncertainty relation and the hydrogen atom. J. Phys. A: Math. Gen. 32, 7691–7696 (1999).
Akhoury, R. & Yao, Y.-P. Minimal length uncertainty relation and the hydrogen spectrum. Phys. Lett. B 572, 37–42 (2003).
Benczik, S., Chang, L. N., Minic, D. & Takeuchi, T. Hydrogen-atom spectrum under a minimal-length hypothesis. Phys. Rev. A 72, 012104(1–4) (2005).
Nozari, K. & Azizi, T. Some aspects of gravitational quantum mechanics. Gen. Rel. Grav. 38, 735–742 (2006).
Ito, D., Mori, K. & Carriere, E. An example of dynamical systems with linear trajectory. Nuovo Cimento A 51, 1119–1121 (1967).
Titchmarsh, E. C. On the relation between the eigenvalues in relativistic and non-relativistic quantum mechanics. Proc. R. Soc. Ser. A 266, 33–46 (1962).
Titchmarsh, E. C. On the relation between the eigenvalues in relativistic and nonrelativistic quantum mechanics (II). Quart. J. Math. 15, 193–207 (1964).
Nogami, Y. & Toyama, F. M. Coherent state of the Dirac oscillator. Can. J. Phys. 74, 114–121 (1996).
Nouicer, Kh. An exact solution of the one-dimensional Dirac oscillator in the presence of minimal lengths. J. Phys. A: Math. Gen. 39, 5125–5134 (2006).
Quesne, C. & Tkachuk, V. M. An exact solution of the one-dimensional Dirac oscillator in the presence of minimal lengths. J. Phys. A: Math. Gen. 38, 1747–1766 (2005).
Betrouche, M., Maamache, M. & Choi, J. R. Three dimensional Dirac oscillator with minimal length: Novel phenomena for quantized energy. Adv.High Energy Phys. 2013, 383957(1–10) (2013).
Snyder, H. S. Quantized space-time. Phys. Rev. 71, 38–41 (1947).
Quesne, C. & Tkachuk, V. M. Lorentz-covariant deformed algebra with minimal length and application to the (1 + 1)-dimensional Dirac oscillator. J. Phys. A: Math. Gen. 39, 10909–10922 (2006).
Quesne, C. & Tkachuk, V. M. Lorentz-covariant deformed algebra with minimal length. Czech. J. Phys. 56, 1269–1274 (2006).
Strange, P. Relativistic Quantum Mechanics, Cambridge: Cambridge University Press (1998).
Erdélyi, A., Magnus, W., Oberhettinger, F. & Tricomi, F. Higher transcendental functions, New York: McGraw-Hill, Vol. II (1953).
Royer, A. Why are the energy levels of the quantum harmonic oscillator equally spaced. Am. J. Phys. 64, 1393–1399 (1996).
Acknowledgements
One of the authors (M.B.) is indebted to Prof. Kh. Nouicer for his interest and his generous assistance throughout this study. Many thanks to him for fruitful discussions and for remarks and suggestions which are helpful for our future research. The work of M. Maamache was supported by the Agence Thématique de Recherche en Sciences et Technologie(ATRST) contract of May 2, 2011 (code pnr: 8/u19/882). The work of J. R. Choi was supported by the Basic Science Research Program through the National Research Foundation of Korea (NRF) funded by the Ministry of Education (Grant No.: 2013R1A1A2062907).
Author information
Authors and Affiliations
Contributions
M.B. performed scientific calculation. M.B., M.M. and J.R.C. wrote the paper.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Rights and permissions
This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivs 3.0 Unported License. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-nd/3.0/
About this article
Cite this article
Betrouche, M., Maamache, M. & Choi, J. Novel characteristics of energy spectrum for 3D Dirac oscillator analyzed via Lorentz covariant deformed algebra. Sci Rep 3, 3221 (2013). https://doi.org/10.1038/srep03221
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep03221
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.



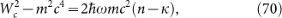
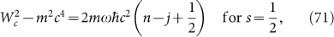
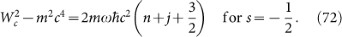
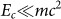 , where Ec being the non-relativistic energy. Indeed, from Eq. (66), we obtain the following formula
, where Ec being the non-relativistic energy. Indeed, from Eq. (66), we obtain the following formula