Abstract
Many complex networks show signs of modular structure, uncovered by community detection. Although many methods succeed in revealing various partitions, it remains difficult to detect at what scale some partition is significant. This problem shows foremost in multi-resolution methods. We here introduce an efficient method for scanning for resolutions in one such method. Additionally, we introduce the notion of “significance” of a partition, based on subgraph probabilities. Significance is independent of the exact method used, so could also be applied in other methods and can be interpreted as the gain in encoding a graph by making use of a partition. Using significance, we can determine “good” resolution parameters, which we demonstrate on benchmark networks. Moreover, optimizing significance itself also shows excellent performance. We demonstrate our method on voting data from the European Parliament. Our analysis suggests the European Parliament has become increasingly ideologically divided and that nationality plays no role.
Similar content being viewed by others
Introduction
Networks appear naturally in many fields of science and are often inherently complex structures. By looking at the modular structure of a network we can reduce its complexity to some extent, yielding a “bird's-eye view” of the network1,2,3.
Although there is no universally accepted definition of a community, there are some commonly accepted principles. We denote by G = (V,E) a graph with nodes V and edges  , where the graph has n = |V| number of nodes and m = |E| number of edges and is said to have a density of
, where the graph has n = |V| number of nodes and m = |E| number of edges and is said to have a density of  . The idea is that in general, we want to reward links within communities with some weight aij, while we want to punish missing links within communities with some weight bij. Working out this idea we arrive at
. The idea is that in general, we want to reward links within communities with some weight aij, while we want to punish missing links within communities with some weight bij. Working out this idea we arrive at

for the “cost” of a partition σ. Here Aij is the adjacency matrix, which is Aij = 1 if there is a link between i and j and zero otherwise, σi denotes the community of node i and δ(σi, σj) = 1 if and only if σi = σj and zero otherwise. This is a slightly more simplified version of the approach by Reichardt and Bornholdt4. We will restrict ourselves here to simple, unweighed graphs.
Different weights aij and bij give rise to different methods. One can imagine for example taking the number of common neighbours as weight bij, the distance of the shortest path or some transition probability in a random walk. Many methods have been developed over the years, but the most noteworthy method is that of modularity5 which uses aij = 1 − pij, bij = pij where pij is some random null-model. It has risen to prominence because it showed encouraging results in various fields, ranging from ecology6,7 and biology8,9 to political science10 and sociology11.
Nonetheless modularity was found to be seriously flawed. Its biggest problem is the resolution limit12,13, which states that modularity is unable to detect relatively small communities in large networks. We showed previously that methods that use local weights (i.e. aij and bij are independent of the graph) do not suffer from the resolution limit14 and are hence called resolution limit free. Within this framework there are relatively few methods that are resolution limit free. One such method is the Constant Potts Model14 (CPM). This model has as weights aij = 1 − γ and bij = γ where γ is a so-called resolution parameter (see next paragraph), resulting in

Rewriting this in terms of communities, we arrive at

where ec is the number of edges within community c (or twice for undirected graphs—this is due to double counting in Σij(Aij − γ)δ(σi, σj) for undirected graphs) and nc is the number of nodes within community c. It can be seen as a variant of the Reichardt and Bornholdt Potts model when choosing an Erdös-Rényi (ER) null model, which assumes that each edge has the same independent probability of being included p. In the remainder of this article, when speaking of a random graph, we refer to an ER random graph, unless explicitly stated otherwise.
It is not too difficult to show that any (local) minimum yields a nice interpretation of the role of the resolution parameter γ. Succinctly stated, communities have an internal density of at least γ and an external density of at most γ. The parameter γ can thus be seen as the desired density of the communities. The central question in this paper is why and how we should choose some resolution parameter γ.
Results
Although CPM does not suffer from the resolution limit, there do remain some problems of scale15. In particular, there is no a-priori way to choose a particular resolution parameter γ. We address this issue in this paper from two complementary perspectives. First we will detail how to efficiently scan different resolution parameters γ for CPM. Secondly, we introduce the notion of “significance” of a partition (which is independent of any method). Both perspectives help in choosing some particular resolution parameter γ. We will demonstrate the method on benchmark networks and show that both scanning for the right resolution parameter as well as optimizing significance itself shows excellent performance. As an application of our method, we analyse a network based on votes of the European Parliament (EP).
Scanning resolutions
Often, various measures of stability—how much does the partition change after some perturbation—are used to determine whether a resolution parameter or a partition is “good”16,17,18,19. In this section we look at stable “plateaus”: ranges of γ where the same partition is optimal. If a partition is optimal over the range of [γ1, γ2] then the communities have a density of at least γ2 and are separated by a density of at most γ1. Hence, the larger this stable “plateau”, the more clear-cut the community structure.
For γ = 0, the trivial partition of all nodes in a single community is optimal (since in that case any cut will increase the cost function). On the other hand, for γ = 1 the optimal partition is to have each node in its own community. This idea holds in general: a higher γ gives rise to smaller communities.
The intuitive idea that a partition should remain optimal for some (continuous) interval of γ can be formalized. More precisely, if σ is an optimal solution for γ1 and γ2, then σ is also an optimal solution for all  (which was also remarked in the supporting information of ref. 10 for a similar method).
(which was also remarked in the supporting information of ref. 10 for a similar method).
Theorem 1. Let  be as in equation (2). If σ* is optimal for both γ1 and γ2, or
be as in equation (2). If σ* is optimal for both γ1 and γ2, or

then  for γ1 ≤ γ ≤ γ2.
for γ1 ≤ γ ≤ γ2.
Proof. First observe that  is linear in γ, which can be easily seen from the definition. Suppose that σ* is optimal in γ1 and γ2. Let γ = λγ1 + (1 − λ)γ2 with 0 ≤ λ ≤ 1, then by linearity of
is linear in γ, which can be easily seen from the definition. Suppose that σ* is optimal in γ1 and γ2. Let γ = λγ1 + (1 − λ)γ2 with 0 ≤ λ ≤ 1, then by linearity of  in γ and optimality of σ* we have
in γ and optimality of σ* we have

Hence  and σ* is optimal for
and σ* is optimal for  .
.
As stated,  is linear in γ and we can rewrite it slightly to emphasize its linearity
is linear in γ and we can rewrite it slightly to emphasize its linearity

where  the total of internal edges and
the total of internal edges and  is the sum of the squared community sizes.
is the sum of the squared community sizes.
It is less obvious how to detect whether a partition remains optimal over some interval. Fortunately, it turns out that N is monotonically decreasing with γ. Specifically, if both partitions are optimal for both resolution parameters, then necessarily N1 = N2 and so also E1 = E2. We therefore only need to find those points at which N(γ) changes, which can be done efficiently using bisectioning on γ.
Theorem 2. Let  , z = 1, 2. Furthermore, let
, z = 1, 2. Furthermore, let  where nc(σz) denote the community sizes of the partition σz. If γ1 < γ2 then N1 ≥ N2.
where nc(σz) denote the community sizes of the partition σz. If γ1 < γ2 then N1 ≥ N2.
Proof. The two partitions σ1 and σ2 have the costs  ,
,  . Both partitions are optimal for the corresponding resolution parameters and we obtain
. Both partitions are optimal for the corresponding resolution parameters and we obtain

Summing both inequalities yields

and so γ1(N1 − N2) ≤ γ2(N1 − N2). Since γ1 < γ2 we obtain that N1 ≥ N2.
Significance
Another, complementary, point of view would be to have some quality measure to state at what resolution γ the partition is “good”. After some reflection, it is ironic we return to the question of what resolution yields a good partition. After all, the initial goal of modularity was in fact to decide on some resolution level: where to cut a particular dendrogram5.
Although modularity compares the number of edges within a community to a random graph, this does not provide any “significance” of a partition, since random graphs and sparse graphs without community structure can also have quite high modularity20,21,22. Other approaches have been suggested that try to estimate in some way the significance of a partition. One recent approach, known as “surprise”, focuses on the probability to find E internal edges in a random graph23,24. Another more “local” approach keeps the degrees constant and asks what the probability is to connect so many edges to a given community25, which led to a method known as OSLOM26. A third approach focuses on the likelihood of generating a graph given a certain partition and degree distribution27, known as stochastic block models.
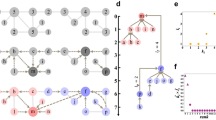
But when thinking about the significance of a partition, most methods go about it the wrong way around23,24,25,26,27. We do not want to know the probability a “fixed” partition contains at least E internal edges, but whether a partition with at least E internal edges can be found in a random graph, which is the approach we will take in this paper. After all, community detection involves searching for some good partition, so we should focus on the probability of finding such a good partition in a random graph. In a way, the earlier approaches assume the partition is “fixed” and the edges are randomly distributed, whereas we try to find a partition in a random graph, which can result in quite different statistics. Stated somewhat differently, earlier approaches ignore that a simple permutation of nodes still contains the same partition—one only needs to identify the permutation to uncover the original partition—whereas our approach does account for that. We illustrate the differences in the two approaches in Figure 1.
Probabilities for partitions.
Consider the example partition provided in (a). The objective is to somehow estimate how (un)likely such a partition occurs in a random graph–the significance of a partition. In (b) and (c) we show the same graph, but in (b) the same partition as in (a) is used, while in (c) a partition with more internal edges is used. For illustrative purposes, the graph is generated by randomly rewiring some of the edges and permuting the nodes of the original graph in (a). Earlier approaches keep the partition fixed and focus on the probability that so many edges fall within the given partition, as illustrated in (b). Yet this ignores there might exist some partition within this graph that has more internal edges. Therefore, we focus on the probability of finding such a dense partition in random graphs, as illustrated in (c).
Nonetheless, these earlier approaches might work quite well. For example, explicitly calculating the probability to find E internal edges, seems to yield good results23,24. Obviously, the two probabilities—surprise and our approach—are not completely independent. If the probability of finding many edges within a partition is high then surely finding a partition with many edges should be easy. On the other hand, if the probability of finding a dense partition is low, then surely the probability a partition contains many edges is low as well. In between these two extremes is a grey area and a more in-depth analysis is required for understanding it exactly.
Although exact results for finding a partition in a random graph are hard to obtain, we do get some interesting asymptotic results. The asymptotic limit we analyse concerns the probability to find a partition into a fixed number of communities with a certain density for n → ∞ in a random graph. The probability for finding a certain partition can be reduced to finding some dense subgraphs in a random graph. We consider subgraphs of size proportional to n, so that it is of size sn, with 0 < s < 1 of a fixed density q. Our central result concerning these subgraph probabilities is the following (the proof can be found in the Methods section). We here use the asymptotic notation f = Θ(g) for denoting g is an asymptotic upper and lower bound for f.
Theorem 3. The probability that a subgraph of size nc and density q appears in a random graph of size n and density p is asymptotically

where D(q || p) is the Kullback-Leibler divergence28

For each p ≠ q the probability decays as a Gaussian, with a rate depending on the “distance” between p and q as expressed by the Kullback-Leibler divergence. Furthermore, the larger the subgraph the less likely a subgraph of different density than p can be found. Combining these probabilities we arrive at the following approximation for the probability for a partition to be contained in a random graph

where pc is the density of community c. We define the significance then as

Notice that for the two trivial partitions of (1) all nodes in a single community (γ = 0) or (2) each node in its own community (γ = 1), the significance is zero (assuming no self-loops). Since the significance is non-negative (because the Kullback-Leibler divergence is non-negative), there will most likely be some partition in between these two extremes (0 < γ < 1) which yields a non-zero significance.
Encoding gain
Notice that the Kullback-Leibler divergence can be interpreted as a kind of entropy difference. It can be written as

where H(q) is the binary entropy and H(q, p) is the cross entropy


Hence, it measures the difference in entropy between p and q, assuming that q is the “correct” probability.
This points to a possible interpretation of the significance  in terms of encoding of the graph. Suppose we are requested to compress the graph G and we do so using the simplest possible framework: for each possible edge we indicate whether it is present or not. Using the average graph density p, by Shannon's source coding theorem28, the optimal code lengths are −log p for indicating an edge is present and −log(1 − p) for indicating an edge is absent. Now suppose that for some community we have the actual density q. The expected code length using the average graph density is then H(q, p). If we use the actual graph density q however, we obtain an expected code length of H(q). The gain in coding efficiency by using q instead of p is then D(q || p). Doing so for all
in terms of encoding of the graph. Suppose we are requested to compress the graph G and we do so using the simplest possible framework: for each possible edge we indicate whether it is present or not. Using the average graph density p, by Shannon's source coding theorem28, the optimal code lengths are −log p for indicating an edge is present and −log(1 − p) for indicating an edge is absent. Now suppose that for some community we have the actual density q. The expected code length using the average graph density is then H(q, p). If we use the actual graph density q however, we obtain an expected code length of H(q). The gain in coding efficiency by using q instead of p is then D(q || p). Doing so for all  possible edges and for all communities then yields the significance (we hence don't count the external edges). Significance can thus be regarded as the gain in encoding a graph by making use of a partition.
possible edges and for all communities then yields the significance (we hence don't count the external edges). Significance can thus be regarded as the gain in encoding a graph by making use of a partition.
Using significance
There are two ways to use significance. Firstly, we could use significance to select a particular resolution parameter γ. As was made clear in the previous subsection, we don't have to scan  if N(γ1) = N(γ2). If in addition we are only interested in the γ for which
if N(γ1) = N(γ2). If in addition we are only interested in the γ for which  is maximal, we can only scan those ranges for which the significance is maximal (taking a greedy approach), similar to root-finding bisectioning.
is maximal, we can only scan those ranges for which the significance is maximal (taking a greedy approach), similar to root-finding bisectioning.
Secondly, we could optimise significance itself. We use an approach similar to the Louvain method29 for optimizing significance (see Methods). Notice that using significance as an objective function is not resolution limit free, contrary to CPM14. After all, given a partition and a graph, pick a subgraph that consists of only a single community. Then the significance  of that partition, defined on the subgraph equals 0, since D(pc || p) = 0. Since this constitutes the minimum, it is unlikely that no other partition provides a higher significance. Hence, the same partition no longer (necessarily) remains optimal on all community induced subgraphs and the method is hence not resolution limit free.
of that partition, defined on the subgraph equals 0, since D(pc || p) = 0. Since this constitutes the minimum, it is unlikely that no other partition provides a higher significance. Hence, the same partition no longer (necessarily) remains optimal on all community induced subgraphs and the method is hence not resolution limit free.
Resolution profile
Scanning the resolution parameters using bisectioning seems to work quite well on LFR benchmark networks30, as displayed in Figure 2. These benchmark networks have n = 103 nodes and have an average degree 〈k〉 = 20 with a maximum degree of Δ = 50 and follow a power-law distribution  with τk = 2. The community sizes range between 20 and 100 and are distributed according to
with τk = 2. The community sizes range between 20 and 100 and are distributed according to  with τc = 1. This corresponds to the settings as used for comparing several algorithms31. The proportion of internal links can be controlled by a so-called mixing parameter 0 ≤ μ ≤ 1, so that for μ = 0 communities are easily detectable, whereas this becomes increasingly difficult for higher μ. For the hierarchical benchmark the mixing parameters μ1 controls the coarser level and μ2 controls the finer level. For more details, we refer to Lancichinetti, Fortunato & Radicchi30.
with τc = 1. This corresponds to the settings as used for comparing several algorithms31. The proportion of internal links can be controlled by a so-called mixing parameter 0 ≤ μ ≤ 1, so that for μ = 0 communities are easily detectable, whereas this becomes increasingly difficult for higher μ. For the hierarchical benchmark the mixing parameters μ1 controls the coarser level and μ2 controls the finer level. For more details, we refer to Lancichinetti, Fortunato & Radicchi30.
Scanning results for directed and hierarchical benchmark graphs.
We display the squared community sizes  , the total internal edges
, the total internal edges  and the significance
and the significance  of each partition (all on a logarithmic axis on the left). The VI (on a linear axis on the right) is calculated over the various results returned by running a stochastic algorithm. If the VI is low, this indicates that the partitions found by the algorithm are (almost) the same. The black dashed line indicates the expected (maximal) significance of an equivalent random graph, which is estimated to be about n log n ≈ 6,908.
of each partition (all on a logarithmic axis on the left). The VI (on a linear axis on the right) is calculated over the various results returned by running a stochastic algorithm. If the VI is low, this indicates that the partitions found by the algorithm are (almost) the same. The black dashed line indicates the expected (maximal) significance of an equivalent random graph, which is estimated to be about n log n ≈ 6,908.
From Figure 2 it is quite clear that both N and E are stepwise decreasing functions of γ. The plateaus indeed correspond to the planted partition for the benchmark network. The “stability” of a partition is reported in terms of the average pairwise variation of information (VI) between the various results of multiple runs of the algorithm. The VI measure can be interpreted as a distance between partitions32, so a low value indicates the results are relatively stable. Indeed, in the range of the plateau, the VI is relatively low (near 0), indicating the partition is relatively stable. Hence, using such heuristics, it seems possible to scan for “stable” plateaus of resolution values. Moreover, significance is highest in the region of the plateaus and thus seems to be able to point to “meaningful” resolutions for these networks.
For hierarchical LFR benchmark graphs30 results are similar (Figure 2). This network has n = 103 nodes and each node has a degree of ki = k = 20. It consists of 10 large communities of 100 nodes each and each large community is composed of 5 smaller communities of 20 nodes each. We observe two plateaus for μ2 = 0.1 (we have used μ1 = 0.1 for both results), corresponding to the two levels of the hierarchy. For these plateaus the VI is near zero, indicating quite stable results. For μ2 = 0.5 the two plateaus have merged into a single plateau, The smaller communities are more significant for μ2 = 0.1. This makes sense, since the smaller communities are quite well defined for this regime, while the larger communities are less clearly defined. Interestingly, when the two plateaus merge for μ2 = 0.5, the significance is lower than for μ2 = 0.1. Indeed, the communities are less clearly defined for μ2 = 0.5 than for μ2 = 0.1. Again, this makes sense, as the smaller communities are much less clearly defined, while most links still fall within the larger community (since μ1 = 0.1).
ER graphs
Applying the same technique as in the previous subsection to ER graphs, we obtain a resolution profile, which shows a particular transition (Figure 3a). This transition can be explained by the asymptotics of significance. As the graph grows and n → ∞, the probability in equation (7) Pr(σ) → 0 for pc ≠ p. This indicates that it becomes increasingly difficult to find (relatively large) subgraphs of a density different from p and in the limit we expect only to find subgraphs of about density p. For γ < p we then expect to find one large community, while for γ > p we expect to obtain each node in its own community, thereby explaining the transition around γ* ≈ p. The asymptotic analysis ignores the fact that the number of communities may grow with the number of nodes. Therefore, it misses the fact that small communities may have a density of pc > p, which explains the somewhat slower increase of number of communities for γ > p.
Results for ER graphs.
In (a) we show that there is a transition around γ = p the density of the graph. This transition can be explained by the subgraph probabilities calculated in this paper, which suggest that asymptotically, a random graph only contains subgraphs of about the same density (of size proportional to n). In (b) we show the significance of random graphs, which seems to scale approximately with n log n.
Analysing how significance behaves in ER graphs provides us with a baseline to compare to observed significance values. Obviously, the maximum significance scales with the size of the graph. In particular, it seems to scale as n log n (Figure 3b). Compared to the benchmark graphs (Figure 2), the significance found in random graphs is rather low, so that significance shows little to no sign of any community structure in ER graphs (although there will be a non-trivial partition obtaining this maximum significance). By comparing the observed significance in any graph to n log n, one is thus able to asses to what extent the observed community structure is significant. We believe this represents a first step towards a fully fledged hypothesis testing of the significance of community structure.
Maximizing significance benchmarks
We have tested the two methods: (1) using significance to choose a γ in CPM; and (2) optimizing significance itself. We used the standard LFR benchmark, with the same parameters as for Figure 2 for the “big” communities, while the “small” communities range from 10 to 50, for both n = 1,000 and n = 5,000. The results are displayed in Figure 4. We measure the performance using the normalized mutual information (NMI)31, with NMI = 1 indicating the method uncovered the planted partition exactly. It is clear that using significance to scan for the best γ parameter for CPM works quite well. Surprisingly however, optimizing significance itself results in a slightly worse performance than scanning for the optimal γ parameter for CPM for some settings. This is presumably due to some local minima in which the significance optimization gets stuck, while this is not the case for CPM. Nonetheless, optimizing significance works quite well and seems to outperform Infomap33,34, which was previously shown to perform well31. The OSLOM method performs relatively well, although not as well as using significance to scan for the best γ parameter for CPM. This method is aimed at overlapping communities, so an adjusted NMI35 was used to account for that, which still equals 1 if it uncovers the planted partition exactly. No results for the significance are provided, since there is no adjusted version of this measure (yet). Modularity clearly shows signs of the resolution limit12, as it has difficulties detecting smaller communities in relatively large networks. In general, all methods have a similar computational complexity and use (variants of) the Louvain method29. Detecting the optimal resolution value γ for CPM involves running the Louvain method multiple times which obviously takes more time.
Benchmark results for significance.
Finding the optimal resolution value for CPM using significance seems to work best (first row), where an NMI of 1 indicates the algorithm uncovers exactly the planted partition (OSLOM might return overlapping communities, we used an adjusted NMI for that35, but it is still 1 if it is correct). Optimizing significance itself also works rather well. We tested two different community size distributions: the small communities are between 10 and 50 nodes and the big communities between 20 and 100 nodes. The resolution limit is clearly visible for modularity, which shows especially for small groups in large networks. Whenever the significance found by each method  is higher than the significance of the planted partition
is higher than the significance of the planted partition  , the planted partition is no longer the optimal partition from the significance point of view (second row). If the significance of the planted partition
, the planted partition is no longer the optimal partition from the significance point of view (second row). If the significance of the planted partition  is lower than the significance of an equivalent random graph
is lower than the significance of an equivalent random graph  no method seems able to correctly detect the planted partition (third row).
no method seems able to correctly detect the planted partition (third row).
Calculating the significance for the planted partition  , we see that in general whenever a method correctly finds the planted communities (i.e. NMI = 1), that the significance of the partition found by that algorithm is equivalent, so that
, we see that in general whenever a method correctly finds the planted communities (i.e. NMI = 1), that the significance of the partition found by that algorithm is equivalent, so that  (second row of Figure 4). We observe a decrease in significance for increasing μ, as expected (third row of Figure 4). At the point where the significance of the planted partition goes below the significance of an equivalent random graph,
(second row of Figure 4). We observe a decrease in significance for increasing μ, as expected (third row of Figure 4). At the point where the significance of the planted partition goes below the significance of an equivalent random graph,  , no method seems able to correctly detect the communities. This suggests that significance accurately captures whether there is some partition present in the network or not. Before this point, whenever a method is unable to detect the planted communities, the significance of that “incorrect” partition is lower than that of the planted partition,
, no method seems able to correctly detect the communities. This suggests that significance accurately captures whether there is some partition present in the network or not. Before this point, whenever a method is unable to detect the planted communities, the significance of that “incorrect” partition is lower than that of the planted partition,  , indicating that the planted partition is of maximal significance.
, indicating that the planted partition is of maximal significance.
European parliament
We demonstrate the method on networks of the European Parliament (EP) from 1979–2009, where each vote of a member of parliament (MEP) for or against a certain proposal is recorded, the so-called roll call votes (these do not constitute all votes in the EP though), similar to an analysis of the U.S. Senate10. Over this whole period, a total of almost 16 million votes were cast, by in total a little over 2,500 different MEPs for more than 21,000 issues. For each parliamentary year (roughly from mid-June to mid-June the next year), we constructed a network, where there is a link between two MEPs whenever they vote more in accord than average. We only take into account votes whenever both MEPs cast a yea or nay vote (instead of abstaining, not voting or being absent). We used data from Simon Hix36.
The MEPs are elected for a five year period from national member states and each MEP is associated to a national party. In total we can discern 169 national parties over the whole period, but usually parties and MEPs organise themselves in political groups (EP groups) that correspond to some ideological views, ranging from liberalism to socialism and from conservatives to progressives. Not all MEPs organise themselves in EP groups; these are known as Non-Attached (NA) members. Although the EP has the power to choose the European Commission (not per individual commissioner, but as a whole), they do not need to organise themselves in governing parties and opposition. Nonetheless, various coalitions are formed and from time to time the largest groups have collaborated in a grand coalition of sorts37. In short, we can create a partition on three different aspects of the MEPs: (1) their EP group; (2) their national party; and (3) their member state. In addition, we obtain the partition that maximizes significance.
We show the normalized significance (i.e. normalized by 〈S〉 ≈ n log n) for the four different possible partitions in Figure 5 from 1979 (the first EP) to 2008 (the sixth EP). Given the (sub) national constituencies of elected MEPs, one particular concern is that the EP is governed by national interests, rather than some common European interest. Our results clearly show that neither a partition based on national party nor on a partition based on member states is significant. To be clear, this does not imply that MEPs of the same national party do not vote similarly (because they do), rather, it means they vote highly similar to MEPs of other parties. For member states however, the division seems to run across member states and MEPs of the same member state do not necessarily vote in a similar fashion. This shows that in general MEPs do not vote along national lines, although for certain votes the national background may play a role38,39.
Results for the European Parliament (EP).
In (a) we show the significance of four different possible partitions throughout time: the partition that maximizes significance and partitions based on the affiliation of each member of parliament (MEP) to an EP group, a national party or a member state. In (b) we show the resolution profile for the sixth EP in the parliamentary year 2008 (June 13, 2008–June 12, 2009). Besides the other quantities, we also show the similarity as measured by the NMI to partitions based on the EP groups, the national parties and the member states. In (c), (d) and (e) we show how such a partition looks like at maximum significance and at two different resolution values γ = 0.5 and γ = 0.8 respectively. The latter corresponds to the partition that maximizes significance. The top shows the division in parliament, while the bottom shows the adjacency matrix ordered the same as the parliament. The division in communities is indicated by the grouping of the seats in parliament and the black lines in the adjacency matrix, while the EP groups are indicated by colour. For a key to the abbreviations of the EP parties, we refer to the main text.
The partition in EP groups shows 5 to 15 times the significance of a random graph, making it quite significant. Whereas the partition into member states and national parties remains almost constant throughout time, the partition into EP groups increases quite a lot from 1979 to 2008, with an all time low of  in 1981 and reaching its maximum of
in 1981 and reaching its maximum of  in 2001, an increase of more than 400%. One possible explanation of the general increase in divisiveness is that the EP has become more powerful over the years, so that competition over important issues have taken a lead37,38,40. Besides a general trend upwards, there seems to be a particularly large jump between 1995 and 1996. One possible explanation is that Austria, Finland and Sweden entered the European Union in 1995, whereafter MEPs were elected to parliament in 1995 and 1996. On the other hand, the accession of Eastern European countries in 2004 and Eastern Balkan countries in 2007 did not seem to increase the divisiveness. The maximum significance closely follows the same trend as the EP group partition, suggesting the two are related.
in 2001, an increase of more than 400%. One possible explanation of the general increase in divisiveness is that the EP has become more powerful over the years, so that competition over important issues have taken a lead37,38,40. Besides a general trend upwards, there seems to be a particularly large jump between 1995 and 1996. One possible explanation is that Austria, Finland and Sweden entered the European Union in 1995, whereafter MEPs were elected to parliament in 1995 and 1996. On the other hand, the accession of Eastern European countries in 2004 and Eastern Balkan countries in 2007 did not seem to increase the divisiveness. The maximum significance closely follows the same trend as the EP group partition, suggesting the two are related.
We have also analysed in the sixth parliament for the year 2008, using CPM and significance, to see what scales of community structure are present. We show results for γ = 0.5 and γ = 0.8, with the latter corresponding to the maximal significance for CPM. Clearly, the communities have a quite high internal density and are quite strongly connected amongst each other, as is also clear from the adjacency matrices displayed in Figure 5.
At γ = 0.5 CPM groups together the Greens/European Free Alliance (G/EFA) and the European United Left/Nordic Green Left (EUL/NGL), which are both left wing environmental parties. The Party of European Socialists (PES), joins the two other leftist parties at a somewhat higher resolution of γ = 0.8. The more conservative parties of the Union for Europe of the Nations (UEN) and the Alliance of Liberals and Democrats for Europe (ALDE) seem to join forces with the more centric European People's Party-European Democrats (EPP-ED). The eurosceptic Independence/Democrats (IND/DEM) group divides itself between the right-wing and the left-wing bloc, although some members constitute a separate bloc with other Non-Attached (NA) MEPs, who themselves also split across the two large blocs. The partition maximizing significance is different still, but shows a similar grouping of EP groups, in addition to several smaller communities. Surprisingly however, a part of UEN is joined with PES, although they seem ideologically more remote.
These three different partitions highlight different aspects of the voting network. The partition maximizing significance for CPM (at γ = 0.8) seems to highlight a more or less traditional partition into left and right wing politics37. The partition for γ = 0.5 seems to reveal a grand coalition37, with mainly the green-left differing from the rest. The partitions maximizing significance itself seems to highlight some interesting split of the UEN. In conclusion, the EP shows signs of multiple possible partitions and significance seems to point to some interesting partitions.
Discussion
We have presented in this paper a method to find significant scales in community structure. Firstly, we introduced a bisectioning method allowing a fast and accurate construction of a resolution profile. Secondly, we suggested a measure based on subgraph probabilities in order to state what partitions are significant. This measure can be interpreted as the gain in encoding a graph by making use of a partition. We showed significance is able to accurately portray partitions in benchmarks. Additionally, we showed on an empirical example using voting data of the European Parliament that this measure conveys meaningful information in that setting. Significance seems to be closely related to the measure of surprise23,24 and to stochastic block models27, relationships we hope to explore further in the future.
We conjectured that the maximum significance 〈S〉 ~ n log n for random graphs, which allows researchers to compare the observed significance to the expected significance. It constitutes a first step towards fully fledged hypothesis testing of the significance of partitions. Nonetheless, a proof of this behaviour is lacking so far. Moreover, the standard error needs to be estimated still, although simulations show it is relatively small. Furthermore, the significance is currently based on Erdös-Rényi graphs, but it might be more realistic to take the degree distribution into account3. Significance is not only useful for partitions found using community detection, but also for partitions based on other node characteristics41, such as school grades42, gender43, or dormitories44, similar to what we did for the European Parliament and as such we deem it to be a valuable contribution to analysing partitions in complex networks.
Methods
Subgraph probabilities
We write  for a random graph G from
for a random graph G from  , such that each edge has independent probability p of being included in the graph, the usual Erdös-Rényi (ER) graphs. We use |G|: = |V(G)| = n for the number of nodes and ||G||: = |E(G)| = m for the number of edges. We use H ⊆ G to denote the fact that H is an induced subgraph of G. We write
, such that each edge has independent probability p of being included in the graph, the usual Erdös-Rényi (ER) graphs. We use |G|: = |V(G)| = n for the number of nodes and ||G||: = |E(G)| = m for the number of edges. We use H ⊆ G to denote the fact that H is an induced subgraph of G. We write  for the probability that H is an induced subgraph of a
for the probability that H is an induced subgraph of a  . Let S(nc, mc) = {G | |G| = nc, ||G|| = mc} denote the set of all graphs with nc = |G| vertices and mc = ||G|| edges. Furthermore, we slightly abuse notation and write
. Let S(nc, mc) = {G | |G| = nc, ||G|| = mc} denote the set of all graphs with nc = |G| vertices and mc = ||G|| edges. Furthermore, we slightly abuse notation and write  for the probability that a graph
for the probability that a graph  contains one of the graphs in S(nc, mc), i.e.
contains one of the graphs in S(nc, mc), i.e.

Let us denote by X the random variable that represents the number of occurrences of a subgraph with nc vertices and mc edges in a random graph. Let XH be the indicator value that specifies whether a subgraph H of order nc = |H| in the random graph equals one of the graphs in S(nc, mc), which of course comes down to

We can then write  where the sum runs over all
where the sum runs over all  possible subgraphs H. Obviously then,
possible subgraphs H. Obviously then,  . By Cauchy-Schwarz's inequality
. By Cauchy-Schwarz's inequality  and Markov's inequality
and Markov's inequality  we obtain the following bounds
we obtain the following bounds

This way of estimating probabilities is known as the second moment method45.
It is convenient to define the probability that a graph of nc nodes contains mc edges

Theorem 4. The expected number of occurrences of an induced subgraph with nc nodes and mc edges in a random graph with n nodes and density p, is given by

Proof. By linearity of expectation, we have  and because XH is an indicator variable
and because XH is an indicator variable  . Notice that H has nc nodes, so that
. Notice that H has nc nodes, so that  and Pr(XH = 1) = r. There are
and Pr(XH = 1) = r. There are  subgraphs of nc nodes in a graph with n nodes, which concludes the proof.
subgraphs of nc nodes in a graph with n nodes, which concludes the proof.
For  the idea is to calculate the expected value of the number of pairs of subgraphs that have mc edges. We do this by separating in three parts: the parts of the two subgraphs without overlap and the part that overlaps.
the idea is to calculate the expected value of the number of pairs of subgraphs that have mc edges. We do this by separating in three parts: the parts of the two subgraphs without overlap and the part that overlaps.
Theorem 5. The expected squared number of occurrences of an induced subgraph can be written as

with 
Proof. The variable X2 can be decomposed into parts XH × XH′, such that we need to investigate the probability that both H and H′ have mc edges. So, we can separate this expectancy in parts of partially overlapping subgraphs, like

where u represents the overlap between the different subgraphs. If H and H′ are (edge) independent, so when u < 1, the answer is simply given by Pr(XH = 1)2. For u ≥ 1 the answer is more involved.
So let us consider two subgraphs H and H′ such that |H ∩ H′| = u ≥ 1. Let us separate this in three independent parts, the overlap Δ = H ∩ H′ and the remainders A = H − Δ and B = H′ − Δ. Clearly then, |Δ| = u and |A| = |B| = nc − u. The probability that ||H|| = ||H′|| = mc can then be decomposed in the probability that the sum of these independent parts sum to mc. The probability that ||H|| = mc can be decomposed as

where m(Δ) signifies the number of edges within Δ. Similarly, we arrive at the conditional probability for both subgraphs H and H′. However, since we have conditioned exactly on the overlapping part, the two remaining parts are independent and we can write

This probability can be calculated and yields

where  . We then obtain
. We then obtain

which leads to

where m(Δ) ranges from 0 to the minimum of mc and the number of possible edges  .
.
Now counting the number of subgraphs that overlap in u nodes, for each choice of subgraph H, we choose u nodes in H and nc − u nodes in the remaining n − nc nodes. In total, there are then

overlapping subgraphs with u nodes in common. Concluding, we arrive at

Writing this out, we arrive at equation (15).
We consider subgraphs of size sn, with 0 < s < 1 with fixed density q. For the asymptotic analysis, we can afford to be a bit sloppy with this density and consider (sn)2 possible edges in the subgraph of sn nodes, so that mc = q(sn)2 and we now denote by S(sn, q) the subgraphs with density q instead of the actual number of edges.
Theorem 6. The probability for a dense subgraph can be bounded below and above asymptotically as

where D(q || p) is the Kullback-Leibler divergence

Proof. We prove the asymptotic result by showing that both an upper and a lower bound have a similar asymptotic behaviour. The upper and lower bounds are provided by Markov's and Cauchy-Schwarz's inequality as stated in equation (12). We will first prove the upper bound. Taking logarithms on Stirling's approximation, we obtain that

where H(p) is the binary entropy

We apply this to  with r as in equation (13) and we obtain
with r as in equation (13) and we obtain

which can be simplified to log  , utilising the binary Kullback-Leibler divergence28
, utilising the binary Kullback-Leibler divergence28

which yields the upper bound by Markov's inequality.
We need the second moment for the lower bound. This can be rewritten as  , with
, with

By Cauchy-Schwarz inequality, we want that

increases as −(sn)2D(q || p). We know that by Jensen's inequality we have

Using the notation u = αsn we can write

We can bound

by

with k = mc − m(Δ), in which we recognize the binomial cumulative probability Pr(Y ≤ mc) where Y are the number of edges in the overlapping part. By Hoeffdings inequality this can be bounded by

Combining with our earlier result on E(X), we then have

For large enough n the quadratic term dominates and we obtain  , giving the lower bound. By combining the lower and upper bound we obtain the asymptotic result stated in the theorem.
, giving the lower bound. By combining the lower and upper bound we obtain the asymptotic result stated in the theorem.
Optimizing significance
As is common in the Louvain method29, we look at the difference of moving some node. However, we also need to aggregate the graph and still correctly move communities. For that we need the node size ni, similar as for CPM14, which initially is ni = 1. Upon aggregating the graph the node size is set to the sum of the node sizes within a community. Moving node i from community r to s with size ni, eir edges to community r and eis edges to community s gives a difference in significance of

where  and
and  .
.
References
Fortunato, S. Community detection in graphs. Phys. Rep. 486, 75–174 (2010).
Porter, M. A., Onnela, J.-P. & Mucha, P. J. Communities in networks. Not. Am. Math. Soc. 56, 1082–1097 (2009).
Newman, M. E. J. Communities, modules and large-scale structure in networks. Nat. Phys. 8, 25–31 (2012).
Reichardt, J. & Bornholdt, S. Statistical mechanics of community detection. Phys. Rev. E 74, 016110 (2006).
Newman, M. & Girvan, M. Finding and evaluating community structure in networks. Phys. Rev. E 69, 026113 (2004).
Guimerà, R. et al. Origin of compartmentalization in food webs. Ecology 91, 2941–2951 (2010).
Stouffer, D. B. & Bascompte, J. Compartmentalization increases food-web persistence. Proc. Natl. Acad. Sci. USA 108, 3648–52 (2011).
Guimerà, R. & Amaral, L. A. N. Functional cartography of complex metabolic networks. Nature 433, 895–900 (2005).
Kashtan, N. & Alon, U. Spontaneous evolution of modularity and network motifs. Proc. Natl. Acad. Sci. USA 102, 13773–8 (2005).
Mucha, P. J., Richardson, T., Macon, K., Porter, M. A. & Onnela, J.-P. Community structure in time-dependent, multiscale and multiplex networks. Science 328, 876–8 (2010).
Conover, M. D. et al. The geospatial characteristics of a social movement communication network. PLoS ONE 8, e55957 (2013).
Fortunato, S. & Barthélemy, M. Resolution limit in community detection. Proc. Natl. Acad. Sci. USA 104, 36 (2007).
Kumpula, J. M., Saramäki, J., Kaski, K. & Kertész, J. Limited resolution in complex network community detection with potts model approach. Eur. Phys. J. B 56, 41–45 (2007).
Traag, V. A., Van Dooren, P. & Nesterov, Y. Narrow scope for resolution-limit-free community detection. Phys. Rev. E 84, 016114 (2011).
Lancichinetti, A. & Fortunato, S. Limits of modularity maximization in community detection. Phys. Rev. E 84 (2011).
Mirshahvalad, A., Lindholm, J., Derlén, M. & Rosvall, M. Significant communities in large sparse networks. PLoS ONE 7, e33721 (2012).
Ronhovde, P. & Nussinov, Z. Multiresolution community detection for megascale networks by information-based replica correlations. Phys. Rev. E 80, 016109 (2009).
Delvenne, J.-C., Yaliraki, S. N. & Barahona, M. Stability of graph communities across time scales. Proc. Natl. Acad. Sci. USA 107, 12755–60 (2010).
Mirshahvalad, A., Beauchesne, O. H., Archambault, E. & Rosvall, M. Resampling effects on significance analysis of network clustering and ranking. PLoS ONE 8, e53943 (2013).
Reichardt, J. & Bornholdt, S. When are networks truly modular? Physica D 224, 20–26 (2006).
Bagrow, J. Communities and bottlenecks: Trees and treelike networks have high modularity. Phys. Rev. E 85, 9 (2012).
Montgolfier, F. D., Soto, M. & Viennot, L. Asymptotic modularity of some graph classes. Lect. Notes. Comput. Sc. 7074, 435–444 (2011).
Aldecoa, R. & Marín, I. Deciphering network community structure by surprise. PLoS ONE 6, e24195 (2011).
Aldecoa, R. & Marín, I. Surprise maximization reveals the community structure of complex networks. Sci. Rep. 3, 1060 (2013).
Lancichinetti, A. Statistical significance of communities in networks. Phys. Rev. E 81, 046110 (2010).
Lancichinetti, A., Radicchi, F., Ramasco, J. J. & Fortunato, S. Finding statistically significant communities in networks. PLoS ONE 6, e18961 (2011).
Karrer, B. & Newman, M. E. J. Stochastic blockmodels and community structure in networks. Phys. Rev. E 83, 016107 (2011).
Cover, T. M. & Thomas, J. A. Elements of Information Theory (John Wiley & Sons, Hoboken, 2012).
Blondel, V. D., Guillaume, J.-L., Lambiotte, R. & Lefebvre, E. Fast unfolding of communities in large networks. J. Stat. Mech. 2008, P10008 (2008).
Lancichinetti, A., Fortunato, S. & Radicchi, F. Benchmark graphs for testing community detection algorithms. Phys. Rev. E 78, 46110 (2008).
Lancichinetti, A. & Fortunato, S. Community detection algorithms: A comparative analysis. Phys. Rev. E 80, 056117 (2009).
Meilă, M. Comparing clusterings–an information based distance. J. Multivar. Anal. 98, 873–895 (2007).
Rosvall, M. & Bergstrom, C. T. Multilevel compression of random walks on networks reveals hierarchical organization in large integrated systems. PLoS ONE 6, e18209 (2011).
Rosvall, M. & Bergstrom, C. T. Maps of random walks on complex networks reveal community structure. Proc. Natl. Acad. Sci. USA 105, 1118–23 (2008).
Lancichinetti, A., Fortunato, S. & Kertész, J. Detecting the overlapping and hierarchical community structure in complex networks. New. J. Phys. 11, 033015 (2009).
Hix, S., Noury, A. G. & Roland, G. Democratic Politics in the European Parliament (Cambridge University Press, Cambridge, 2007).
Kreppel, A. & Hix, S. From “grand coalition” to left-right confrontation: Explaining the shifting structure of party competition in the european parliament. Comp. Polit. Stud. 36, 75–96 (2003).
Noury, A. G. Ideology, nationality and euro-parliamentarians. Eur. Union. Polit. 3, 33–58 (2002).
Hix, S., Noury, A. & Roland, G. Voting patterns and alliance formation in the european parliament. Philos. Trans. R. Soc. Lond. B. Biol. Sci. 364, 821–31 (2009).
Hix, S., Noury, A. G. & Roland, G. Power to the parties: Cohesion and competition in the european parliament, 1979–2001. Br. J. Polit. Sci. 35, 209–234 (2005).
Bianconi, G., Pin, P. & Marsili, M. Assessing the relevance of node features for network structure. Proc. Natl. Acad. Sci. USA 106, 11433–8 (2009).
Stehlé, J. et al. High-resolution measurements of face-to-face contact patterns in a primary school. PLoS ONE 6, e23176 (2011).
Palchykov, V., Kaski, K., Kertész, J., Barabási, A.-L. & Dunbar, R. I. M. Sex differences in intimate relationships. Sci. Rep. 2, 370 (2012).
Traud, A. L., Mucha, P. J. & Porter, M. A. Social structure of facebook networks. Physica A 391, 4165–4180 (2012).
Bollobás, B. Random Graphs (Cambridge University Press, Cambrige, 2001).
Acknowledgements
We acknowledge support from Actions de recherche concertées, Large Graphs and Networks of the Communauté Française de Belgique and from the Belgian Network DYSCO (Dynamical Systems, Control and Optimization), funded by the Interuniversity Attraction Poles Programme, initiated by the Belgian State, Science Policy Office.
Author information
Authors and Affiliations
Contributions
V.T. and G.K. analysed the resolution profile construction. V.T. analysed subgraph probabilities and wrote the main manuscript. P.V.D. reviewed the analysis. All authors reviewed the manuscript.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Rights and permissions
This work is licensed under a Creative Commons Attribution-NonCommercial-ShareALike 3.0 Unported License. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-sa/3.0/
About this article
Cite this article
Traag, V., Krings, G. & Van Dooren, P. Significant Scales in Community Structure. Sci Rep 3, 2930 (2013). https://doi.org/10.1038/srep02930
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep02930
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.