Abstract
We report a novel technique for label-free, rapid visualization of structure and dynamics of live cells with nanoscale sensitivity through traditionally opaque media. Specifically, by combining principles of near-infrared (NIR) spectroscopy and quantitative phase imaging, functional characterization of cellular structure and dynamics through silicon substrates is realized in our study. We demonstrate the efficacy of the new approach by full-field imaging of erythrocyte morphology in their native states with a nm path length sensitivity. Additionally, we observe dynamic variations of human embryonic kidney cells, through a silicon substrate, in response to hypotonic stimulation with ms temporal resolution that also provides unique insight into the underlying biophysical changes. The proposed technology is fundamentally suited for high-performance investigations of biological specimens and significantly expands the options for visualization in complex microfluidic devices fabricated on silicon.
Similar content being viewed by others
Introduction
Since its original conception, optical microscopy has provided an incredibly powerful tool for fundamental investigations in medicine and biology, with significant recent attention being focused on improving the resolution and contrast of the microscopic image. Typically, contrast is enhanced in imaging of optically thin specimens (including live cells) by attachment of contrast agents, such as stains and fluorescent dyes, to the structure(s) of interest. Despite remarkable advances in this area1, label-free microscopy is highly desirable to study the dynamics and physiological activity of various cellular and sub-cellular scale processes under natural conditions. The challenge of generating endogenous contrast is commonly addressed by exploiting intrinsic light-matter interactions, such as variations in refractive index (elastic Rayleigh scattering)2,3, absorption4 and Raman scattering5,6,7.
Of these, the most commonly used endogenous contrast mechanism is optical phase with its applications to biological imaging of cells dating back to Zernike's development of phase contrast microscopy (PCM)8,9. PCM and its derivatives including differential interference contrast microscopy10, provide contrast of nearly transparent samples by transforming the phase information into the intensity distribution and thus revealing the structural details of biological systems without necessitating staining. However, the resulting phase contrast image is an intensity distribution, in which the phase information is coupled nonlinearly and cannot be retrieved quantitatively11. Over the past decade, several investigators, including our own laboratories, have focused on extraction of quantitative phase images with extremely high path length sensitivity over time periods from milliseconds to a cell life cycle12,13,14,15,16,17,18,19. Quantitative phase microscopy (QPM) and its advanced variants, provides detailed cellular thickness (morphology) and refractive index information thereby permitting enhanced discrimination of details in inter-cellular components. The sensitivity of these field-based microscopic techniques has enabled the study of miniscule changes in cellular state, such as fluctuations of the cellular membrane (e.g. red blood cell “flickering”20) and the correlation of these changes with different patho-physiological conditions including pathogen infection21 and metabolic regulation of cell shape22.
A substantive milestone in the further development of quantitative phase microscopy resides in enabling such measurements in/through a variety of different media/substrates. The overarching goal of such efforts is to overcome the effects of sample turbidity (defined here as the interplay of optical absorption and multiple scattering) in order to unveil the structures located behind the turbid biological tissue23,24. One of the critical steps in this direction is to establish visualization capabilities through traditionally opaque media, where the absorption component represents the primary hindrance. Such a development would also have extensive implications for measurements in complex microfluidic devices and lab-on-a-chip systems fabricated on silicon, which have been elegantly employed for a variety of applications ranging from synthetic chemistry to bioanalysis and medical diagnostics25,26. Indeed, because of the prolific use of silicon-based electronic devices, a well-developed tool kit for creating micro- and nanoscale structures has been derived from semiconductor fabrication technology leading to advanced silicon based lab-on-a-chip devices that facilitate complex object manipulation, transport and control27,28. Suitably combining quantitative phase microscopy with silicon lab-on-chip systems can, therefore, provide a uniquely powerful platform capable of wide-field, high-resolution, label-free sensing in precisely actuated and controlled cellular processes.
In order to address this unmet need, we propose a novel route to characterization of biological structures through traditionally opaque media by combining interferometry-based quantitative phase retrieval with a lower energy (higher wavelength) illumination source. In particular, the incorporation of a near infrared (NIR) source permits visualization through silicon substrates - since silicon has low absorption in the NIR range - and deeper penetration into biological tissue while minimizing photo-thermal damage29,30. Indeed, we show that using a NIR illumination source in a transmission imaging arrangement enables biological structure visualization and measurement capabilities through silicon-based platforms, comparable to conventional visible light-based QPM through a glass substrate. To validate our proposed approach, we demonstrate the key features for complete on-chip particle imaging and characterization. First, a suitable illumination wavelength is selected by considering the transmission efficiency and the fringe contrast of the recorded quantitative phase images. With the chosen wavelength of incident light, we compute the sensitivity of our NIR phase microscope to temporal path length changes. Significantly, we employ the optimized system for mapping the phase profile and determining the corresponding topography of live red blood cells through silicon substrates – with nanoscale path length sensitivity. Finally, we exhibit the versatility of our method for observing dynamic changes in more complex cell model systems (HEK293 cells), placed on silicon wafers, in response to hypotonic stimulation and thus in elucidating the relationship between such stimuli and corresponding changes in cell morphology and physiology.
Results
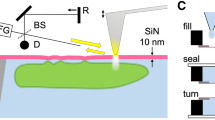
To quantify nanoscale path length changes and image through traditionally opaque substrates, our phase microscope combining NIR illumination with a near common-path interferometer was used (Figure 1). The system, which has been detailed in one of our previous reports31, employs a spatial-filtering based near common path geometry that leads to increased phase stability by avoiding a separately generated reference wave (more information in Methods section). Since a silicon-based camera was used to record the resulting fringe patterns, an important step in performance characterization was to determine the optimal wavelength by striking a balance between transmission efficiency through the silicon wafer and detection efficacy of the NIR signal. The former was measured for 5 discrete wavelengths (960 nm, 980 nm, 1000 nm, 1020 nm and 1040 nm) to assess the attenuation trend with respect to wavelength for our system. For these measurements, the power of the Ti: Sapphire laser was kept constant at 14.7 mW and the power of the beam transmitted through the wafer and the collection optics was gauged by a power meter (PM100D, Thorlabs Inc.). Expectedly, the transmission through the silicon substrate increases with wavelength in the NIR region of interest. Further, to analyze the obtained image quality, fringe contrast was quantified from measurements performed for the aforementioned wavelengths. This is particularly important because clarity and stability of the first diffraction order, which is obtained from the Fourier transform of the interference pattern, largely depends on the contrast of the recorded fringes. Fringe contrast, C, was calculated using Equation (1) in terms of the observed intensity maxima (Imax) and minima (Imin) in the acquired interference pattern.

Supplementary Figure 1(a) shows the change in fringe contrast as a function of wavelength. One can observe the sharp decrease in fringe contrast with increase in wavelength in the NIR region. The change in fringe contrast can also be visualized from the respective interference patterns at 960 nm and 1040 nm provided in Supplementary Figure 1(b) and (c), which is directly attributable to the drop in quantum efficiency of the silicon-based camera at the higher wavelengths. Taking into consideration the transmission efficiency through the silicon substrate and, more importantly, the fringe contrast, a wavelength of 980 nm was selected for the ensuing imaging studies. It is worth noting that the optimal wavelength depends on the application of interest and could be different from the one used for our experiments here depending on the characteristics of the chosen substrate (e.g. material, doping and thickness) as well as the detector employed.
Schematic of the near-infrared quantitative phase microscope (NIR-QPM) setup employing a near-infrared illumination source (Ti: Sapphire laser) to acquire images of biological samples through an opaque silicon substrate.
CDL: Condenser lens; CLL: Collimating Lens; MO: Microscopic objective; BS1 & BS2: Beam splitters; M1, M2 & M3: Mirrors; FL: Focusing lens; CMOS: Complementary metal–oxide–semiconductor camera.
With the selected wavelength of incident light, the stability of the instrument and thus the sensitivity of cell topography to dynamic changes were subsequently evaluated via phase noise computations. For this purpose, sets of 100 silicon wafer only (no-sample) images were acquired at 3 frames per second and noise analysis was performed on the entire field of view as well as at single points. The temporal phase fluctuations can be described by the respective standard deviations – where the standard deviations set the limit to the lowest values of phase change that the instrument can detect. The phase fluctuations can be readily translated to changes in path length (which represents a more meaningful parameter for topography measurements) by using Eq. (S1) of the Supplementary Information Sec. S1. From Supplementary Figure 1(d), the spatial standard deviation of the optical path length associated with the full field of view is observed to have a temporal average of 0.7 nm and a temporal standard deviation of 0.04 nm. For a single point (3 × 3 pixel average), the corresponding standard deviation is computed to have temporal average and standard deviation of 6.13 nm and 2.25 nm, respectively. These measurements validate our ability to visualize quantitative phase images at the ca. 2 nm path length scales through the silicon substrate.
Subsequently, to study the accuracy of our system in retrieving phase profiles, measurements were performed on calibration samples. Figure 2 shows an example of such measurements, obtained from imaging polystyrene microspheres (PS06N/5878, Bangs Lab, USA, diameter d = 6.02 ± 0.37 μm, refractive index n1 = 1.57) using a 40X/0.65NA microscope objective. In order to better mimic a transparent biological specimen (i.e. a phase object), the polystyrene beads were immersed in oil (refractive index n2 = 1.51). The resultant refractive index contrast achieved between the particles and the surrounding medium was 0.06. Figures 2(a)–(c) indicate the intermediate steps in reconstruction of the quantitative phase image. Figure 2(a) provides the interferogram recorded from the polystyrene microspheres by the CMOS detector that was then Fourier transformed to yield Figure 2(b). This figure clearly illustrates the presence of the zero and first orders, of which the latter was filtered using the angular spectrum method. Figure 2(c) shows the strongly wrapped phase image – which when unwrapped gives the final quantitative phase image given in Figure 2(d). Based on the peak phase value of the polystyrene microsphere in the field of view, the value of n1 (refractive index of the polystyrene particle) was determined using Equation (2) to be 1.569 ± 0.02. The computed value shows an excellent match with the values indicated by the manufacturer and the small uncertainty in our computation can be ascribed to the impurities present in the solution, residual imperfections of the imaging beam and inexact knowledge of the microsphere diameter.

where n1, n2 are refractive indices of the sample and surrounding medium respectively, d is the sample thickness, λ being the wavelength of interferometric beam and φ is the measured phase. Further, in order to illustrate the ability of NIR-quantitative phase microscope (NIR-QPM) to provide detailed information about single cell structure and dynamics, we analyzed fresh erythrocytes (red blood cell, RBC) kept in isotonic solution (0.9% NaCl concentration) and placed on the silicon wafer. The cells were imaged in typical culture conditions and no further preparation, such as fixation, was performed in order to best preserve their natural state and morphology. Here, interferograms of RBCs were obtained using a 40X/0.65NA microscope objective (Figure 3(a)). Due to the lack of fixation, one can observe that one of the three RBCs in the field of view is tilted at an angle relative to the imaging axis. Figure 3(b) and 3(c) shows the corresponding strongly wrapped and pseudocolor quantitative phase image of the RBCs, respectively, where the individual cells are easily identifiable. Remarkably, the well-known discocyte shape of the RBCs can be observed through the silicon substrate with a temporal resolution of 70 ms. Also, it is evident that the tilted RBC exhibits higher phase values in relation to the other RBCs in the field of view, due to the greater optical thickness. From Figure 3(c), one of the RBCs was selected and measured for the phase values across its transverse cross-section. The resultant phase profile is plotted against position in μm in Figure 3(d).
Imaging of microspheres through silicon substrate.
(a) NIR interferogram of 6 μm polysterene beads in immersion oil. (b) FFT of the recorded interferogram and selection of the first diffraction order, as marked by the green square. (c) Wrapped phase image. (d) Surface plot representation of the unwrapped quantitative phase image. The color bar represents the retrieved phase at each point of the image.
Label-free, full-field visualization of red blood cell (RBC) morphology.
(a) Interferogram of RBCs in the field of view. (b) Wrapped phase image. (c) Pseudocolor quantitative phase image with the inset box representing the selection of a single RBC for which the phase profile is determined. (d) Graph showing the optical phase profile and the thickness profile of the selected RBC as a function of the transverse dimension. Here, it can be observed that the well-known discocyte shape of the RBCs is retrieved by quantitative phase imaging through the silicon substrate.
Since (mature) RBCs do not possess nuclei and major organelles and are almost exclusively comprised of hemoglobin (i.e. 97% of the dry content), they can be modeled as optically homogeneous objects, as noted previously16. In other words, the phase information retrieved by the proposed approach can be expeditiously translated into thickness information, which in turn can be utilized to probe other relevant morphological parameters such as cell shape and volume. Specifically, thickness of the RBC was computed from the above transverse phase profile using a re-arranged version of Equation (2), where refractive index values of 1.33 and 1.39 were used for the medium and RBC21, respectively. The thickness profile is overlaid with the phase profile of the RBC in Figure 3(d). The values of thickness at the thickest point (in the range of 2.3–2.5 μm) and that in the center of the RBC (ca. 1.5 μm) are consistent with prior observations using other modalities including atomic force microscopy. Nevertheless, such a full-field topographic image with sub-micron accuracy cannot be achieved using other conventional methods, a majority of which also requires extensive sample preparation.
Finally, the novel NIR-QPM system was employed to investigate the kinetics of changes in eukaryotic cells in response to hypotonic stimulation. Such stimulation has been reported to cause morphological and biophysical changes in cells32, leading to physiological changes including release of adenosine triphosphate (ATP)33. In addition to serving as a useful model for testing the viability of the measurement method for dynamic studies, hypotonic stimulation is also of fundamental interest due to its widespread application for dissolution and absorption of drugs in intramuscular injections. For our experiments, HEK 293 (human embryonic kidney) cells were maintained at 37°C, 5% CO2 in Dulbecco's modified Eagle medium containing 10% fetal bovine serum. The cells were then grown on poly-D-lysine coated coverslips and embedded between the coverslip and the silicon wafer. To induce hypotonic shocks, predetermined amounts of distilled water were added next to the culture medium, which was originally in the isotonic state (300 mOsm/kg). All the measurements were performed at room temperature and off-axis interferograms were recorded in a time-lapse series, before as well as after the hypotonic shock.
Figure 4(a) shows the bright field image of an agglomeration of (six) HEK 293 cells in isotonic solution using a 40X/0.65NA microscope objective. The corresponding QPM measurements are provided in Figure 4(b) (interferogram), 4(c) (wrapped phase image) and 4(d) (unwrapped phase image). In order to better track the morphological changes in a single cell, we also imaged using a 100X/1.25NA objective. Figure 5(a), (b) and (c) show the interferogram, wrapped phase image and the unwrapped surface phase plots, respectively. For hypotonic stimulation, distilled water was added to first change the osmolarity of the media to 215 mOsm/kg and subsequently to 187 mOsm/kg. One may expect that due to the hypotonic shocks, cell swelling will be induced leading to increase in geometrical thickness and, therefore, to larger values of optical thickness. To the contrary, we observe there is a clear decrease in phase values after the hypotonic shock(s) from Figure 5(d) and (e). We conjecture that while swelling of the HEK cells leads to an increase in geometric thickness, this effect is counter-balanced by the concomitant reduction in the intracellular refractive index. The latter is also caused by the influx of water, which has a lower refractive index of 1.33 in relation to that of the cell (in the range of 1.36 to 1.39)17. From a biological standpoint, this can be explained as the effect of dilution of intracellular proteins that largely determine the mean integral refractive index of the cell. Indeed, the decrease in tonicity from 215 to 187 mOsm/kg causes further influx of fluid inside the cell resulting in even greater protein dilution and an evident decrease in phase, as visualized from the relative differences between Figure 5(d) and (e).
Visualization of HEK 293 cells sandwiched between a glass coverslip and the silicon substrate.
(a) Bright field image of an agglomeration of HEK cells in isotonic solution. (b) Interferogram recorded from the HEK cells in the field of view. (c) Wrapped phase image. (d) Unwrapped quantitative phase image.
Investigation of dynamic processes at the cellular level.
(a), (b) & (c) show the recorded interferogram, wrapped phase image and the unwrapped surface phase plots, respectively, of a single HEK cell in isotonic DMEM solution. (d) and (e) provide the surface phase plot representations after the induction of the hypotonic shocks. Specifically, the osmolarity of the extracellular media for (d) and (e) was 215 mOsm/Kg and 187 mOsm/Kg, respectively. (f) Time-lapse phase trace for six representative cells, wher the points of hypotonic stimulation are highlighted by the yellow bands. The variation of phase values of the background is also provided.
To characterize the change in phase values, a time-lapse phase trace is plotted in Figure 5(f) for six representative cells (the variation of phase values of the background is also given). The instantaneous phase for a specific cell was calculated from the average of the phase values over its spatial spread. For each of the cells, the time trace shows two transition stages associated with the first and second hypotonic shock application, respectively. In quantitative terms, the mean phase value for the six cells before stimulation was calculated to be 2.14. After the first hypotonic shock, this decreases to 1.83 and after the second hypotonic shock it further reduces to 1.4. Despite the observed inter-cellular variance in phase values, the large disparity in the mean values before and after the hypotonic shocks for each cell highlights the morphological and biophysical changes caused by such stimulation. In other words, hypotonic stimulation displays a “phase” signature that can be detected by the proposed approach, due to its unprecedented sensitivity, speed and ability to visualize through opaque media. Similarly, many other cellular processes appear to have a phase signature including pathogen infection, cell signaling, cell growth and metabolic changes21,22. As such, this new label-free route to rapid, nanoscale imaging through silicon substrates may help to systematically study and better identify the cellular and molecular mechanisms that produce these phase signatures.
Discussion
Our proposed approach shows remarkable capability of label-free, visualization of different biological structures with nanoscale sensitivity and high temporal resolution through silicon substrates. Given the promising nature of our results, we envision that the substantive advantages of the proposed approach in terms of full-field, label-free imaging with high temporal resolution will pave the way for a large array of biosensing applications, especially in lab-on-chip platforms. For example, our studies open the door to non-perturbative investigations of neuronal activity under external stimuli, especially in interface with silicon devices. Studies in this area could provide valuable insight of the interface between biology and materials important to device design and control. Critically, this novel optical tool also offers a wealth of possibility in high throughput analysis for disease diagnostics and drug screening as well as in future point-of-care measurements, driven in large part by its ability to deliver remarkable sensitivity at relatively affordable costs. Evidently, this approach can be advantageously employed for the study of mechanical, chemical and electric perturbation of different types of cells on silicon-based microfluidic and multi-electrode array platform, as represented by the schematic of the lab-on-chip system (Figure 6). The richness and diversity of applications that can be studied is pictured in the schematic ranging from investigations of pathological conditions in red blood cells to high throughput drug screening and neuronal activity.
Schematic of the lab-on-chip system for the study of mechanical, chemical and electric perturbation of different types of cells on silicon-based microfluidic and multi-electrode array platform.
Quantitative phase image of a human embryonic kidney cell and RBC imaged through silicon is shown on the top.
Our present efforts can also be significantly advanced by pushing the laser wavelength further into the infrared region, especially above 1150 nm. This will enable visualization of cells through thicker silicon substrates that may be employed for specific sensing or lab-on-chip applications. It is worth noting that the absorption in the silicon sample is primarily a function of the thickness and doping of the substrate and the wavelength of light used34,35. Besides limiting the transmitted laser power, absorption can cause photon-induced currents in devices and may lead to localized sample heating. Photon-induced currents, in particular, can restrict the ability to make concurrent measurements with on-chip electronic sensors while using the QPM laser source. Moving to higher wavelengths would significantly mitigate these issues due to substantive reduction in substrate absorption. Evidently, operation in this wavelength range would necessitate the replacement of the existing silicon-based CMOS detector with a camera better suited for infrared image acquisition, such as an indium gallium arsenide (InGaAs) focal plane array detector. Such a camera would considerably improve fringe contrast at higher wavelengths, thereby boosting overall image quality.
It may be noted that while the axial sensitivity is few nm, the lateral resolution is diffraction limited (0.61 λ/NA). In our case (λ = 960 nm), use of 40x/0.65 NA objective leads to transverse resolution of 900 nm and use of 100x/1.25NA objective provides improved transverse resolution of 468 nm. Interestingly, the figures of merit of the proposed approach (acquisition rate, transverse resolution, temporal and spatial sensitivity) can be upgraded by incorporating methods that are commonplace in quantitative phase imaging in the ultraviolet-visible wavelength region. For example, one may incorporate an NIR broadband source (“white light” illumination36) that would reduce random speckle-based interference patterns resulting in more spatially uniform images. In fact, improvements in path length sensitivity to sub-nanometer levels would allow fundamental investigations of stiffness and migration behavior of different types of cells. While quantitative phase images provide estimation of the morphology change based on the assumption that the refractive index of the cell is homogeneous, integrating tomographic phase microscopy approach17,37 or dual-medium method31, with the technique presented here, can allow better quantitative interpretation of morphological changes by decoupling refractive index values from measured phase values. Combining such a method with a more chemically-specific analytical tool, such as vibrational spectroscopy38,39, may permit unparalleled understanding of the morphological and chemical components of the cell and their interactions.
In conclusion, we have developed a new route to imaging through traditionally opaque media by combining the principles of NIR illumination with quantitative phase microscopy. We have designed and developed a NIR-QPM system to image through opaque silicon substrates and characterize samples with nanoscale path length sensitivity and approximately 70 ms temporal resolution. Using our unique instrumentation, we have performed functional characterization of cellular structure and dynamics through silicon substrates. Specifically, we have shown the efficacy of the proposed approach in mapping the topography of red blood cells in their native states through silicon substrates with a path length sensitivity of ca. 2 nm. Additionally, we have demonstrated the ability to observe dynamic variations of HEK 293 cells, on silicon wafers, in response to hypotonic stimulation and investigate the underlying biophysical mechanisms.
Methods
The NIR QPM system employs a spatial-filtering based near common path geometry that leads to increased phase stability by avoiding a separately generated reference wave. Briefly, a tunable Ti: Sapphire laser (MaiTai HP, Newport-Spectra Physics) was used for NIR illumination in the range of 960–1040 nm prior to selection of optimal wavelength (980 nm), based on the optimal combination of transmission efficiency and interference fringe contrast. The beam was directed through a condenser (CL) to illuminate the sample(s), positioned on a silicon wafer (double side polished, 100 μm thickness (University Wafer, USA)) as would be done for trans-illumination microscopy. This substrate was comparable in thickness to that of the No. 0 cover slip (0.085–0.13 mm thick) that is extensively used in high-resolution microscopy studies. Nevertheless, this should not be interpreted as representing the maximum thickness that is likely to be employable after further optimization of optical detection parameters. Light transmitted through the sample-silicon wafer was collected by a microscopic objective (MO) (40X/0.65NA, Edmund Optics or 100X/1.25NA, Model: E Plan, Nikon depending on the specific application) and was split into two beams by a beam splitter (BS1). Removal of the higher order frequencies in the Fourier transform plane by use of spatial filtering results in a uniform intensity distribution that can then be used as a reference beam. Both the sample and reference beams were directed toward a second beam splitter (BS2) and were recombined. The second beam splitter was placed at a small angle with respect to the reference beam resulting in off-axis interferometry. The interference pattern was recorded by a CMOS camera (1280 × 1024 pixels, pixel size 5.2 μm, DCC1545M, Thorlabs) and images were acquired at 14 frames per second (i.e. temporal resolution of ca. 70 milliseconds), unless otherwise mentioned. The acquired fringe patterns were processed by in-house image reconstruction algorithms (Supporting Information, Sec. S1) coded in MATLAB®.
References
Tsien, R. Y. The Green Fluorescent Protein. Ann. Rev. Biochem. 67, 509–544 (1998).
Thekkek, N. & Richards-Kortum, R. Optical imaging for cervical cancer detection: solutions for a continuing global problem. Nat. Rev. Cancer 8, 725–731 (2008).
Soares, J. S. et al. Diagnostic power of diffuse reflectance spectroscopy for targeted detection of breast lesions with microcalcifications. Proc. Natl. Acad. Sci. USA 110, 471–476 (2013).
Kong, R., Reddy, R. K. & Bhargava, R. Characterization of Tumor Progression in Engineered Tissue using Infrared Spectroscopic Imaging. Analyst 135, 1569–1578 (2010).
Dingari, N. C., Horowitz, G. L., Kang, J. W., Dasari, R. R. & Barman, I. Raman Spectroscopy Provides a Powerful Diagnostic Tool for Accurate Determination of Albumin Glycation. PLoS ONE 7, e32406 (2012).
Stadler, J., Schmid, T. & Zenobi, R. Nanoscale Chemical Imaging Using Top-Illumination Tip-Enhanced Raman Spectroscopy. Nano Lett. 10, 4514–4520 (2010).
Kang, J. W., Nguyen, F. T., Lue, N., Dasari, R. R. & Heller, D. A. Measuring Uptake Dynamics of Multiple Identifiable Carbon Nanotube Species via High-Speed Confocal Raman Imaging of Live Cells. Nano Lett. 12, 6170–6174 (2012).
Zernike, F. Phase-contrast, a new method for microscopic observation of transparent objects. Physica 9, 686–698 (1942).
Zernike, F. How I Discovered Phase Contrast. Science 345–349 (1955).
Murphy, D. Differential interference contrast (DIC) microscopy and modulation contrast microscopy. Fundamentals of Light Microscopy and Digital Imaging, 153–168 (Wiley-Liss, New York, 2001).
Popescu, G. Quantitative Phase Imaging of Cells and Tissues (McGraw-Hill, New York, 2011).
Cuche, E., Bevilacqua, F. & Depeursinge, C. Digital holography for quantitative phase-contrast imaging. Opt. Lett. 24, 291–293 (1999).
Popescu, G. et al. Fourier phase microscopy for investigation of biological structures and dynamics. Opt. Lett. 29, 2503–2505 (2004).
Marquet, P. et al. Digital holographic microscopy: a noninvasive contrast imaging technique allowing quantitative visualization of living cells with subwavelength axial accuracy. Opt. Lett. 30, 468–470 (2005).
Mann, C., Yu, L., Lo, C. M. & Kim, M. High-resolution quantitative phase-contrast microscopy by digital holography. Opt. Exp. 13, 8693–8698 (2005).
Popescu, G., Ikeda, T., Dasari, R. & Feld, M. Diffraction phase microscopy for quantifying cell structure and dynamics. Opt. Lett. 31, 775–777 (2006).
Choi, W. et al. Tomographic Phase Microscopy. Nat. Meth. 4, 717–719 (2007).
Yu, L. F. et al. Quantitative phase evaluation of dynamic changes on cell membrane during laser microsurgery. J. Biomed. Opt. 13, 050508 (2008).
Yu, L. et al. Digital holographic microscopy for quantitative cell dynamic evaluation during laser microsurgery. Opt. Exp. 17, 12031–12038 (2009).
Popescu, G., Badizadegan, K., Dasari, R. & Feld, M. Observation of dynamic subdomains in red blood cells. J. Biomed. Opt. 11, 040503 (2006).
Park, Y. et al. Refractive index maps and membrane dynamics of human red blood cells parasitized by Plasmodium falciparum. Proc. Nat. Acad. Sci. USA 105, 13730–13735 (2008).
Park, Y. et al. Metabolic remodeling of the human red blood cell membrane. Proc. Natl. Acad. Sci. USA 107, 1289–1294 (2010).
Vellekoop, I. M. & Mosk, A. P. Universal Optimal Transmission of Light Through Disordered Materials. Phys. Rev. Lett. 101, 120601 (2008).
Kim, M. et al. Maximal energy transport through disordered media with the implementation of transmission eigenchannels. Nat. Photon. 6, 581–585 (2012).
Wei, J., Buriak, J. M. & Siuzdak, G. Desorption–ionization mass spectrometry on porous silicon. Nature 399, 243–246 (1999).
Beebe, D. J., Mensing, G. A. & Walker, G. M. Physics and Applications of Microfluidics in Biology. Ann. Rev. Biomed. Eng. 4, 261–286 (2002).
Krivitsky, V. et al. Si nanowires forest-based on-chip biomolecular filtering, separation and preconcentration devices: nanowires do it all. Nano Lett. 12, 4748–56 (2012).
Hui, E. E. & Bhatia, S. N. Micromechanical control of cell-cell interactions. Proc. Natl. Acad. Sci. USA 104, 5722–5726 (2007).
Appleyard, D. C. & Lang, M. J. Active particle control through silicon using conventional optical trapping techniques. Lab Chip 7, 1837–1840 (2007).
Kang, J. W. et al. Combined confocal Raman and quantitative phase microscopy system for biomedical diagnosis. Biomed. Opt. Exp. 2, 2484–2492 (2011).
Cardenas, N. & Mohanty, S. Decoupling of geometric thickness and refractive index in quantitative phase microscopy. Opt Lett. 38, 1007–1009 (2013).
Tan, Y. et al. Biophysical characterization of hematopoietic cells from normal and leukemic sources with distinct primitiveness. Appl. Phys. Lett. 99, 083702 (2011).
Shinozuka, K. et al. Participation of ATP in cell volume regulation in the endothelium after hypotonic stress. Clin. Exp. Pharmacol. Physiol. 28, 799–803 (2001).
Hecht, E. Optics, 119–131 (Addison Wesley, San Francisco, 4th ed. 2002).
Soref, R. A. & Bennett, B. R. Electrooptical effects in silicon. IEEE J. Quantum Electron. 23, 123–129 (1987).
Wang, Z. et al. Spatial light interference microscopy (SLIM). Opt. Exp. 19,1016–1026 (2011).
Cardenas, N. & Mohanty, S. K. Optical tweezers assisted quantitative phase imaging led to thickness mapping of red blood cells. Appl. Phys. Lett. 103, 013703 (2013).
Kodali, A. K., Llora, X. & Bhargava, R. Optimally designed nanolayered metal-dielectric particles as probes for massively multiplexed and ultrasensitive molecular assays. Proc. Nat. Acad. Sci. 107, 13620–13625 (2010).
Barman, I. et al. Raman spectroscopy based sensitive and specific detection of glycated hemoglobin. Anal. Chem. 84, 2474–2482 (2012).
Acknowledgements
I.B., N.C.D., J.S.S. and R.R.D. wish to thank the National Institute of Biomedical Imaging and Bioengineering grant, 9P41EB015871-26A1. B.J., N.C. and S.K.M. would like to thank Nanoscope Technologies LLC for the equipment grant and support. J.S.S. would also like to acknowledge the support of CNPq fellowship.
Author information
Authors and Affiliations
Contributions
I.B., N.C.D. and S.M. conceived the project. B.J., N.C. and S.M. performed the experiments. B.J., I.B., N.C.D., N.C., J.S.S. and S.M. analyzed the data. All authors reviewed the manuscript and contributed to writing of the paper. R.R.D. and S.M. supervised the project.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Electronic supplementary material
Supplementary Information
Supplementary Info
Rights and permissions
This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivs 3.0 Unported License. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-nd/3.0/
About this article
Cite this article
Joshi, B., Barman, I., Dingari, N. et al. Label-free route to rapid, nanoscale characterization of cellular structure and dynamics through opaque media. Sci Rep 3, 2822 (2013). https://doi.org/10.1038/srep02822
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep02822
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.