Introduction

In classical physics, all observable quantities have an objective reality. The outcome of measuring a classical observable A can not be influenced by a property of the observer or by the choice to simultaneously co-measured A with a second observable B. This property is referred to as non-contextual realism.

Distinctively, in quantum theories the measurement outcome for an observable A depends on what you choose to co-measure at the same time. There exist certain sets of observables where it is impossible to simultaneously assign pre-existing outcomes. In this scenario there is no joint probability distribution from which the measurement statistics for every observable can be recovered as marginals.

Recently Klyachko, Can, Binicioglu and Shumovsky introduced a 5-ray (KCBS) inequality1. The KCBS inequality bounds the maximum attainable level of correlation between outcomes of 5 observables, A1, …, A5, under the dual assumptions that only Ai and A(i + 1 mod 5) are co-measurable and that it is possible to preassign outcomes to all five observables in accordance with non-contextual realism2. By construction the KCBS inequality is satisfied by all non-contextual hidden variable models. However Klyachko et. al. discovered violation of the inequality in a 3-level quantum system. Setting aside Bell type tests of nonlocality3, it has been shown that the KCBS inequality is the simplest possible test for contextuality of quantum theories, in the sense that any inequality based on projective measurements along less than five different direction will be satisfied by all classical and quantum theories4. The KCBS inequality formed the basis of several recent experimental tests of quantum contextuality. Lapkiewicz et. al. have experimentally demonstrated violation of the KCBS inequality in an indivisible 3-level quantum system (furnished by a single photon)5. This experiment built upon a robust and rapidly developing body of experimental contextuality literature6,7,8,9,10,11. In our present work we draw on the tests outlined in these papers.

From the perspective of an experimental test of non-contextual realism the KCBS inequality is a state dependent test; for a sufficiently pure state there exists a choice of five measurement directions which can be used to detect violation of the KCBS inequality. Hence any experimental implementation requires a rigorous state preparation phase. For 3-dimensional systems there also exists a completely state independent test involving thirteen projectors developed by Oh and Yu12 and an almost state independent test involving nine projectors13. The latter is capable of revealing contextuality in every state, except the maximally mixed state, provided we choose the measurement basis appropriately. We describe this inequality in more detail in the following section. It has been shown that thirteen rays is the minimum number of distinct projector directions necessary for a state independent test of non-contextual realism14.

The purpose of this paper is to propose an experimental setup for testing the almost state independent inequality from Ref. 13. The experimental set up will be along the lines of Lapkiewicz et al.'s KCBS inequality experiment5. This provides an ideal platform for examining the recent debate over whether Lapkiewicz et al.'s setup is a faithful experimental implementation of contextuality tests based on n-cycle computability relation graphs, see5,15. We present an adaptation of the circuit which makes this issue transparent and could even be used to check the level of faithfulness empirically. We will also discuss the minimum detector efficiency required to ensure the results are independent of any auxiliary assumptions about photons in undetected events.

Results

Consider a theory with n observables, A1, … An, where each observable, Ai, returns outcome ai with probability p(Ai = ai). This theory exhibits classical realism whenever there exists a joint probability distribution for the combined measurement outcomes p(A1 = a1, …, An = an) such that the measurement statistics, p(Ai = ai), of each observable, Ai, can be obtained as a marginal of this distribution16. In this scenario there exists a non-contextual hidden variable model, conditioned on a set of parameters Λ. The joint probability distribution is reproduced through

where each strategy for assigning measurement outcomes, λ, has weighted probability p(λ) on the set Λ and p(Ai = ai|λ) is the conditional probability of obtaining an outcome ai when measuring observable Ai (for the given noncontextual hidden variable λ).

Quantum theories do not necessarily exhibit non-contextual realism. When we measure an observable A1 we simultaneously collapse the state we are observing onto an eigenstate of A1. If A1 is independently simultaneously co-measurable with either member of a non-commuting pair (A2 and A3), then choosing to measure A1 simultaneously with A2 (respectively A3) can erase information about the correlations between A1 and A3 (respectively A2). Because a joint measurement of A1 and A2 can erase different information from a joint measurement of A1 and A3, the two joint measurements do not need to be unitarily equivalent. The choice to simultaneously co-measure A1 with either A2 or A3 can influence the outcome of A1. We say that these two non-commuting observables each furnish a context for and is compatible with, A1 and that quantum mechanics is a contextual theory.

Given a set of observables we can succinctly represent which subsets are compatible in a single graph. This graph has one vertex, vi, for each observable Ai. The edge set of the graph is generated by connecting any two vertices vi and vj associated with co-measurable observables, respectively Ai and Aj, by an undirected edge (vi, vj).

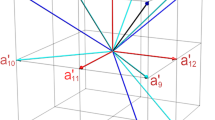
As a concrete example consider the graph in Figure 1 which outlines the compatability relations for a collection of nine observables in a three level system. These nine dichotomic {+1, −1}-observables, A1, …, A9, can be associated with projective measurements along nine rays in a 3-dimensional Hilbert space according to the relation:

By construction these observables obey an exclusivity relation; for any set of mutually compatible observables Ai, Aj, Ak the outcomes Ai = −1, Aj = −1 and Ak = −1 are exclusive. In other words when a measurement is made on a mutually commuting set of observables at most one observable will have outcome −1. If we try to preassign noncontextual outcomes to the nine observables in Figure 1 which obey these exclusivity relations then we find the preassigned values always satisfy:

However it was demonstrated in Ref. 13 that given a quantum state ρ, which is not the maximally mixed state, it is possible to choose a basis for the 3-dimensional Hilbert space so that Inequality (3) will be violated. More explicitly, the state ρ violates Inequality (3) when rays used to define the observables A1, …, A9 are expressed in this basis13. Optimal violation will be obtained when we choose to measure with respect to the eigenbasis of ρ. To complement this analysis we have run a numerical simulation, using QI Mathematica package17, which effectively tested Inequality (3) for a prefixed measurement basis and a randomly generated sample of ten million density matrices weighted by the Hilbert-Schmidt measure. We found 49.98% of quantum states ρ violated (3). A more detailed derivation of Inequality (3) is given in the Methods. In the following section we outline a proposal for experimentally testing Inequality (3).

Figure 1
figure 1

The graph, G, of the computability relations for the nine observables, A1, …, A9, in the inequality 3 which is originally from Ref. 13.

Full size image

Experimental design

We propose an experimental test of Inequality (3) for an indivisible 3-level quantum system furnished by a single photon. A photonic qutrit uses two distinct spatial paths for the photon and within one of the spatial paths two optical modes propagate as distinct polarization modes. The core component is a scheme for simultaneous measurements of pairs of compatible observables Ai and Aj when the corresponding vertices vi and vj are connected by an edge in Figure 1 which uses ideas from Lapkiewicz et al.'s recent experiment5. An implicit caveat on any experimental implementation of this proposal is that all experimental runs must be independent and the results after a statistically significant number of runs must represent an unbiased sampling from the joint probability distribution (1); in the case where the latter is tailored to the nine projective measurement constructed from (7). Later we will discuss how losses and detector inefficiencies may allow a joint probability distribution conditioned on a hidden variable to violate Inequality (3). In both scenarios we use a single photon heralded source which will alow us to monitor photon losses. Previous experiments5,7, produce pairs of polarization entangled photons in the singlet state via parametric down conversion and subsequently rerouted one photon to an auxiliary detector ‘detector 0’. Post selecting on whether this auxiliary detector clicks creates a heralded single photon, see the Supplementary material for a detailed schematic. Any desired initial state can be synthesized using polarizing beam splitters to combine the two spatial modes and half wave plates to transform the polarization components inside a single spatial mode.

We introduce a single detector for each mode (we will use the label: detector i, for i = 1, 2 or 3). Two scenarios are considered: in the first scenario there are no losses and detector i will click whenever a photon is in the corresponding mode |i〉. In the second scenario we will allow for inefficient detectors. We revisit this scenario later. It is convenient to identify the three orthogonal modes with rays |1〉, |2〉 and |3〉 from Equation (7). If detector i clicks then we record Πi = 1 and using Equation (2) we assign a value Ai = −1 to the corresponding dichotomous observable.

The correlations of two dichotomous observables are given by:

The second line follows because (with unit probability) either both Ai and Aj are equal to 1 or alternatively precisely one of them is equal to −1. We only count results from experimental runs where a single detector clicks coincidentally with detector 0. This implies that in all events contributing to Equation (4) the sum of the measurement outcomes for the dichotomous observables (during a single run) is equal to −1 (in the first instance A1 + A2 + A3 = −1). Furthermore when Ai and Aj correspond to orthogonal modes we discount experimental runs where Ai = Aj = −1 causing P(Ai = Aj = −1) = 0. In these circumstances it is pertinent that the projectors |1〉, |2〉 and |3〉 in Equation (7) form a complete basis for the 3-dimensional Hilbert space. When sampling only from events where a single detector clicks, the measured correlations:

obey the completeness relation. Under these experimental circumstance it is optional whether the above correlations need to be measured. A similar relation holds for the complete basis |7〉, |4〉 and |8〉. We clarify that this completeness relation is not a fundamental assumption for deriving Equation (3), rather it is an optional simplification of the experiment which is available because these types of experiments post select on events where a single detector clicks coincidentally with detector 0. This is a natural assumption in most experiments.

Repeated runs of this experimental configuration can be used to measure the correlations 〈A1A2〉, 〈A1A3〉 and 〈A2A3〉. A full experiment capable of measuring all the correlation in Inequality (3) can be obtained by adding standard optical elements; specifically half wave plates and polarizing beam splitters. If we pass the input modes |1〉, |2〉 and |3〉 through a series of half wave plates and polarizing beam splitters then we can output the orthogonal modes for any three rays |i〉, |j〉 and |k〉 which are a linear combination of |1〉, |2〉 and |3〉 and form a basis for the 3-dimensional Hilbert space. At every stage of the experiment each detector is aligned to detect photons in a single mode. It is assumed that this detector will click if the photon is in the corresponding mode.

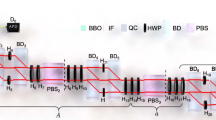
A schematic of the sequence of optical elements and measurements needed to obtain all the correlations in Inequality (3) is depicted in Figure 2. The physical implementation of this experiment will require exact details regarding the sequence of half wave plates and polarizing beam splitters needed to appropriately mix the two different polarization modes within a single spatial mode and subsequently mix the spatial modes. We leave the nuances of the setup to the discretion of an experimental group. However in the supplementary material we give a more detailed account of an explicit realization as a proof of principle that the schematic given in Figure 2 is physically realizable using an adaptation of Lapkiewicz et al.'s design5.

Figure 2
figure 2

Each subfigure represents an experimental configuration which measures 〈AiAj〉 for the specific Ai and Aj indicated on the righthand side of the subfigure.

Orthogonal modes are represented by horizontal lines. Sequences of half wave plates and polarizing beam splitters are labeled T1, …, T8 and detector positions are indicated by the corresponding dichotomous observable. The expectation value 〈A9〉 can be obtained from the data collected during the experimental runs depicted in subfigures 6) or 7). The vertical line through the detectors in subfigures 1) and 3) indicate it is not necessary to record data during these stages. This follows from Equation (5). The precise sequence of optical elements T1, …, T8 are recorded in the Supplementary material. In this schematic when two consecutive stages of the experiment involve measuring the same mode, |i〉 and the beam line of mode |i〉 is unobstructed between the points at which these two measurements are made, we assume the physical implementation will measure the (same) mode |i〉 in two different contexts.

Full size image

It is implicitly assumed that at any stage of the experiment; if a given mode's beam line is not interrupted by an optical element then there is perfect transmission of any photon (amplitude component) in this mode. This occurs regardless of whether the other two modes pass through a half wave plate or are obstructed.

Notice that according to Figure 2, we first measure the mutual correlations of the dichotomous observables, A1, A2, A3, corresponding to orthogonal modes |1〉, |2〉 and |3〉. Subsequently in subfigure 5) we need to measure 〈A2A5〉, however during the intermediary stages the beam line of mode |2〉 has been interrupted. This introduces a source of error. We must recreate the mode |2〉 before measuring 〈A2A5〉. We can not be certain that in both instances we are measuring the precisely the same orthogonal mode |2〉. Correspondingly we introduce a new label to distinguish between the observable A2 in subfigure 1) and the observable measured in subfigure 5) of Figure 2.

In order to find the correlation term 〈A2A5〉 we set up the experiment with the intention of measuring however we create a time delay, Δt, for all photons in mode |2〉 by increasing the optical path length at the point where mode |2〉 is first created. This will ensure that photons originally in mode |2〉 will reach a detector Δt seconds later than the click of the heralding detector, D0. Whereas photons originally in modes |1〉 and |3〉 will result in detection events where D0 clicks coincidently with one of the other three detectors. We now can calculate the correlation term 〈A2A5〉 using Equation (4) and assigning outcome A2 = 1 and A5 = −1 to all runs where detector 5 clicks coincidently with the auxiliary detector D0 and analogously letting outcome A2 = −1 and A5 = 1 correspond to all runs where one of the other two detectors clicks Δt seconds later than the auxiliary detector D0. This procedure generalizes to measuring the correlations 〈A3A6〉 and 〈A8A6〉, see the schematic 2. We highlight that the physical implementation of this scheme will involve changing the (path length of the) beam line depicted in subfigure 5) of Figure 2. In theory any operation preformed on a photon originally created in mode |2〉 will have no effect on the outcome of the compatible observable A5; in practice imperfect reconstruction of mode |2′〉 (and the orthogonal mode |5〉) may lead to violation of the no-disturbance principle. As a result there should be a careful analysis of the number of events where detector 5 clicks Δt seconds later than the heralding detector. These events where the photon is recoded to have been in both modes |2〉 and |5〉, equivalently A2 = A5 = −1, indicate a violating of the exclusivity condition.

Finally we highlight that Equation (5) implies we do not need to collect data during the experimental stages depicted in subfigures 1) and 3) of Figure 2. We have drawn a vertical line through the detectors whenever it is not necessary to collect data. We include these stages in the schematic because it is important to comprehensively set up all the measurement configurations. We need to ensure the orthogonal modes have the same relative orientations (and orthogonality relations) as the projectors in Equation (7). This makes it essential to setup all stages of the experiment.

Errors will arise from imperfect alignment of half wave plates. This will cause some of the modes to be be misaligned with the rays in Equation (7). In this case we will be testing Inequality (3) using projective measurement along directions which do not perfectly match the list in Equation (7). The nine direction in Equation (7) corresponded to a theoretically optimal set of projective measurements for testing Inequality (3). The errors introduced by half wave plate misalignment will make it more difficult to experimentally violate this inequality. However they will not invalidate any experimental results which directly demonstrate violation.

Discussion

We highlight that instead of measuring the correlation term 〈A2A5〉 using the time delay of the photon to register the event A2 = −1, we could have modified Inequality (3),

to include the error terms , , . This would allow us to treat the correlation term identically to all other previous measurements. However the error term would require us to redo the above analysis of 〈A2A5〉 in the almost identical case of ; again using the time delay of the photon to register an event where A2 = −1 and the clicks of detector 2′ to record events where . After collecting the data we can choose to use it to evaluate Inequality (6) and/or Inequality (3); in practice these two experiments are equivalent up to postprocessing of the data. This approach of measuring the modified Inequality (6) closely mirrors ideas from Lapkiewicz et al.'s experiment5. In this context it has been argued that experimentally testing Inequality (6) does not constitute a proper test of a noncontextual inequality15. The controversy arises because mode |2〉 which is originally measured in the context of modes |1〉 and |3〉 must be reconstructed before we measure the correlation term ; this has instigated a debate on whether experimental implementations of Inequality (6) do measure precisely the same observable A2 in two different contexts. In the spirit of Lapkiewicz et al.'s experiment5 the condition for claiming observables A2 and are the same measurement in two different contexts is that they return identical empirical results; if they do not the error term will compensate. We note that using this approach the data collected (and therefore correlations measured) is identical no matter how it is post processed; and that if there is still ambiguity then we can evaluate both Inequalities to determine whether they are empirically equivalent.

Any implementation of this proposal faces more critical problems from the key assumption that results collected during this experiment represent an unbiased sampling from the joint probability distribution (1). This requires us to make subsidiary assumptions about the states of undetected photons unless the detection efficiency is above a minimum thresh hold value 82%. A detailed calculation is given in the next section.

Under these conditions, the above procedure could be used to experimentally test of the inequality from Ref. 13. This implementation would probe one of the foundational principles distinguishing quantum mechanics from classical realistic descriptions of the world. Furthermore if this test reveals contextual behavior in an indivisible spin one system then the behavior can not stem from entanglement. This result complements work done on the KCBS inequality1,5 as well as the thirteen projector state independent inequality from Ref. 7, 12. We present numerical studies which indicate Inequality (3) is violated by 49.98% of states in a 3-level system. This makes an experimental test less sensitive to state preparation.

Methods

In this section we revisit the mathematical details required to derive Inequality (3) and the detector efficiency threshold needed to beat the no-detection loophole in this experiment.

Inequality (3) is based on nine projective measurements whose compatibility relations are provided by orthogonality and depicted in Figure 1. The nine vertices in Figure 1 can be identified with projective measurements Πi = |i〉〈i|, along the following nine rays in a 3-dimensional Hilbert space:

In a non-contextual theory, for any set of orthogonal rays {|i〉, |j〉, …} it is possible to assign values of 1 or 0 to the corresponding projectors {Πi, Πj, …}, in such a way that the outcomes Πi = 1 and Πj = 1 are exclusive and if a projector, Πi, appears in two different orthogonal sets then it is assigned the same consistent value in each set18.

It follows that for any non-contextual realistic theory, where measurement statistics can be encapsulated in a hidden variable strategy p(λ) as in (1), these nine-projectors satisfy:

The exclusivity relations of the dichotomic observables defined in Equation (2) are inherited directly from the exclusivity relations of the corresponding projectors, Πi = |i〉〈i|. Hence the principles and principles and assumptions behind Inequalities (3) and (8) are equivalent. We can derive Inequality (3) directly from this result, by using Equation (2) to replace each of the projectors in Inequality (8) by the corresponding dichotomous observable.

We note that any violation of the exclusivity conditions may lead to higher violations of Inequality (3)19,20,21.

These inequalities are violated by all quantum state ρ except the maximally mixed state, provided we choose the basis for the 3-dimensional Hilbert space appropriately.

Detector inefficiency

A key assumptions in our proposed experimental test of Inequality (3) was that the results collected during a statistically significant number of runs represented an unbiased sampling from the joint probability distribution (1). In the presence of no-detection events however this assumption needs to be re-examined.

In any realistic experiment there will be runs where the photon is lost and none of the detectors click. These losses are caused by reflections off half wave plates and detector inefficiencies. In the proposed experimental scheme we only collect data from experimental runs where a single detector clicks; this automatically discounts any non-detection events. To claim the results of the proposed experiment represent an unbiased sampling from the joint probability distribution (1) we must assume the probability of loosing a photon is not correlated with the measurement outcome. In other words we must assume something about the state of the photon we never measured. Here we describe how efficient the experiment must be in order to eliminate this assumption.

Without loss of generality we can assume all photons are lost at the detector. We attribute an efficiency η to each of the three detectors. We want to make our results independent of the distribution of photon modes in undetected runs. To do this we include the runs where none of the detectors click. The combined total number of runs is constituted by runs where either a single detector clicks or none of the detectors click.

In the ideal scenario where there are no losses, p(Ai = ai) is the probability of getting outcome ai when you measure observable Ai. When we include losses we use p′(Ai = ai) = ηp(Ai = ai) for the proportion of the combined total number of runs where we measure Ai and get outcome ai.

To uniquely specify the results of a run we must specify the outcomes ai, aj and ak of all three dichotomous observables (respectively Ai, Aj and Ak).

When estimating the correlations in Equation (4) we now use the renormalized probability:

which is the ratio of the number of runs with the given outcome (Ai = ai, Aj = aj, Ak = ak) to the number of runs where a single detector clicks. This eliminates the dependence on no detection events (runs with outcome Ai = Aj = Ak = 1).

In hidden variable theories we can use (1) to express as a function of the detector efficiency η and probabilities in the ideal scenario where there are no losses:

This allows us to evaluate the correlations in Equation (4) for a hidden variable strategy p(λ) conditioned on λ. We find Inequality (3) is modified in the presence of detector inefficiency to

We need η > 0.82 for the right hand side of Equation (11) to be below the maximum level of quantum violation for this inequality22. Hence when the detector efficiency is below 82% it is impossible to experimentally detect violation of Inequality (3) unless subsidiary assumptions are made about the distribution of putative outcomes (which detector failed to click) for undetected events.