Abstract
The controlled manipulation of the charge carrier concentration in nanometer thin layers is the basis of current semiconductor technology and of fundamental importance for device applications. Here we show that it is possible to induce a persistent inversion from n- to p-type in a 200-nm-thick surface layer of a germanium wafer by illumination with white and blue light. We induce the inversion with a half-life of ~12 hours at a temperature of 220 K which disappears above 280 K. The photo-induced inversion is absent for a sample with a 20-nm-thick gold capping layer providing a Schottky barrier at the interface. This indicates that charge accumulation at the surface is essential to explain the observed inversion. The contactless change of carrier concentration is potentially interesting for device applications in opto-electronics where the gate electrode and gate oxide could be replaced by the semiconductor surface.
Similar content being viewed by others
Introduction
In photo-conductors, photo-diodes and photo-transistors illumination causes the generation of free charge carriers in normally depleted regions of the device1. The working principle in these devices is different from a MOSFET (metal-oxide-semiconductor field-effect-transistor) where an applied electric field at the gate electrode causes inversion from the p-type gate to n-type in order to switch the transistor into a “current on” state. Recent developments on nanowire transistors could offer an alternative to MOSFETs without the need of layer inversion and junctions2. Charge coupled devices are another important class of photo sensitive devices where inversion of a p-type semiconductor is the basis for its functionality: a gate bias drives the semiconductor substrate to deep depletion and photo-generated holes are removed from the surface region, while electrons are accumulated until surface charge saturation is reached. In a range of the depletion width (up to ~300 nm) the semiconductor substrate becomes inverted. In technologically important transparent conducting oxides, such as In2O3 or SnO2, intrinsic or photo-induced charge accumulation at surfaces or interfaces changes near-surface carrier concentrations, i.e. the electronic properties. Examples are the n-type conductivity of In2O33, the photo-induced Schottky barrier in photorefractive materials with SnO2 electrodes4, or the enhancement of photocurrents in SnO2 nanowires by the decoration with metallic nanoparticles, which is attributed to the formation of Schottky junctions in the vicinity of the nanoparticles5.
Changes in charge-carrier concentration and dopant type in the bulk are usually detected by macroscopic measurements (e.g. conductivity, Hall-effect, capacitance-voltage profiling (C-V)) which also require the presence of junctions and leads. Scanning probe microscopy techniques allow to carry out time-resolved local mapping of photo-generated charge carriers with lateral resolutions in the sub-hundred nanometer range and temporal resolution of less than hundred μs6,7,8. Here, the presence of photo-induced charge carriers is detected indirectly by changes of the resonance frequency of a cantilever or by changes of the potential offset between a cantilever and the sample surface. By contrast, the positively charged muon μ+ represents a very sensitive local probe to detect variations in charge-carrier concentrations as a function of temperature and doping in semiconductors without the need of electrical contacts or the application of electric fields/currents9,10,11,12. In this context local probe means that the implanted μ+, which comes to rest at an interstitial site, is directly interacting with the free charge carriers in its local, nanometer sized environment.
In this paper we demonstrate that we can use illumination to controllably generate persistent charge carriers beneath the surface of nominally undoped, commercial n-type Ge wafers. These charge carriers are detected at tunable depths  with low-energy muon spin rotation (LE-μSR)13,14 using the LE-μSR spectrometer (LEM) at the Swiss Muon Source SμS at PSI. Our results imply that the photo-generated electrons are trapped in surface states which causes the semiconductor near-surface region to convert from n- to p-type. This demonstrates that it is in principle possible to create a configuration similar to a MOSFET without using gate electrodes and gate voltages.
with low-energy muon spin rotation (LE-μSR)13,14 using the LE-μSR spectrometer (LEM) at the Swiss Muon Source SμS at PSI. Our results imply that the photo-generated electrons are trapped in surface states which causes the semiconductor near-surface region to convert from n- to p-type. This demonstrates that it is in principle possible to create a configuration similar to a MOSFET without using gate electrodes and gate voltages.
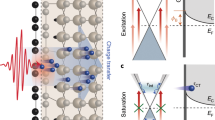
A low-energy μ+ beam with tunable energies in the keV range allows depth-dependent investigations of near-surface regions on a nanometer scale, as shown in Fig. 1. This is different to conventional bulk μSR studies, where energetic muon beams with an energy of typically 4 MeV are used to stop the muons deep inside the sample at depths of the order of hundred micrometer. Note that muon implantation energies <14 keV result in average muon stopping depths that are well-matched with the absorption profile of light in Ge. In a semiconductor or insulator it can capture one or two electrons to form the different charge states of muonium [Mu, (μ+e−), mass of  proton mass]. Depending on factors such as the dopant concentration and Mu formation energy it occurs in one of three, possibly coexisting, charge states Mu+, Mu0 or Mu−, analogous to hydrogen9,10,11,12. The muon decays with a lifetime of 2.2 μs into a positron and two neutrinos. The detection of the various Mu states occurs by observation of the anisotropic distribution of decay positrons which are preferentially emitted along the μ+ spin direction. This anisotropic decay is the basis for the muon spin rotation technique (μSR)9. In μSR experiments on semiconductors, where the muonium has been often used as a light pseudo-isotope of isolated hydrogen, the different Mu charge states can be distinguished by their different spin precession signatures in a magnetic field B applied transverse to the initial muon spin direction. In case of a Mu+ or a Mu− state the muon spin precesses with a frequency ωμ = γμB, where γμ/2π = 135.54 MHz/T is the gyromagnetic ratio of the muon. This precession appears as an oscillation in the recorded muon decay histograms of several positron detectors surrounding the sample. The amplitude A of this oscillation is the muon decay asymmetry and is proportional to the polarization of the corresponding Mu state. In Mu0 the hyperfine coupling causes the muon spin to precess at frequencies that are much higher than ωμ. This allows one to clearly distinguish Mu0 states from Mu+ and Mu−. The latter are often referred as diamagnetic MuD which means a μ+ without unpaired electrons nearby, while Mu0, with an unpaired electron in the vicinity of the μ+, is referred to as being paramagnetic. In an experiment where Mu0 and MuD coexist, but the frequencies of Mu0 are too high to be resolved, the observed decay asymmetry AD will be less than the maximal value. This reduction of AD is commonly called a “missing” fraction. The presence of free charge carriers usually causes depolarization of the Mu state (i.e. a damping of A as a function of time) either by electron or hole capture, or by spin-exchange collisions with conduction electrons, as we will discuss in detail later. Hence, investigations of the depolarization of Mu can provide detailed information regarding the concentration and the type of free charge carriers in the sample.
proton mass]. Depending on factors such as the dopant concentration and Mu formation energy it occurs in one of three, possibly coexisting, charge states Mu+, Mu0 or Mu−, analogous to hydrogen9,10,11,12. The muon decays with a lifetime of 2.2 μs into a positron and two neutrinos. The detection of the various Mu states occurs by observation of the anisotropic distribution of decay positrons which are preferentially emitted along the μ+ spin direction. This anisotropic decay is the basis for the muon spin rotation technique (μSR)9. In μSR experiments on semiconductors, where the muonium has been often used as a light pseudo-isotope of isolated hydrogen, the different Mu charge states can be distinguished by their different spin precession signatures in a magnetic field B applied transverse to the initial muon spin direction. In case of a Mu+ or a Mu− state the muon spin precesses with a frequency ωμ = γμB, where γμ/2π = 135.54 MHz/T is the gyromagnetic ratio of the muon. This precession appears as an oscillation in the recorded muon decay histograms of several positron detectors surrounding the sample. The amplitude A of this oscillation is the muon decay asymmetry and is proportional to the polarization of the corresponding Mu state. In Mu0 the hyperfine coupling causes the muon spin to precess at frequencies that are much higher than ωμ. This allows one to clearly distinguish Mu0 states from Mu+ and Mu−. The latter are often referred as diamagnetic MuD which means a μ+ without unpaired electrons nearby, while Mu0, with an unpaired electron in the vicinity of the μ+, is referred to as being paramagnetic. In an experiment where Mu0 and MuD coexist, but the frequencies of Mu0 are too high to be resolved, the observed decay asymmetry AD will be less than the maximal value. This reduction of AD is commonly called a “missing” fraction. The presence of free charge carriers usually causes depolarization of the Mu state (i.e. a damping of A as a function of time) either by electron or hole capture, or by spin-exchange collisions with conduction electrons, as we will discuss in detail later. Hence, investigations of the depolarization of Mu can provide detailed information regarding the concentration and the type of free charge carriers in the sample.
Schematic of experimental setup and muon stopping and light absorption profiles in germanium.
Muon stopping profiles at the indicated implantation energies were calculated with the Monte-Carlo code TrimSP29,30 from 1 keV to 20 keV. A light absorption coefficient α ~ 5 · 105/cm has been assumed for the used blue light sources with peak wavelengths of 470 nm and 405 nm31, corresponding to photon energies of 2.6 and 3.0 eV, respectively. The pressure at the sample was ≤10−8 mbar.
Results
The samples were nominally undoped commercial Ge (100) wafers from CrysTec GmbH (Berlin, Germany) and MTI corporation (Richmond CA, USA), two side epi polished. The CrysTec sample with a thickness of 0.15 mm was a mosaic of nine 10 × 10 mm2 pieces, with a nominal resistivity ρ = 30 Ωcm (charge carrier density n ~ 5 × 1013 cm−3), as specified by the supplier. Four pieces of the Ge wafers have been sputtered with Au to create a nominally 20-nm-thin Au layer on top of the Ge wafers. The MTI sample had a thickness of 0.5 mm and a diameter of 1″, with ρ = 50–60 Ωcm (n ~ 3 × 1013 cm−3). The samples were glued with conductive silver on a silver coated aluminum sample plate of the cryostat. The sample size assures that more than 95% of the muon beam (12 mm full-width-at-half-maxium) is hitting the sample. The light was generated with two sources (for details, see Methods): i) 33 commercial white and blue LEDs mounted in series on a ring inside the radiation shield of the sample cryostat with a maximum intensity of 10 mW/cm215, or ii), a commercial blue LED point source outside the vacuum chamber for higher intensities up to 80 mW/cm2. For the white LEDs we measured a light transmission of 40–50% through the 20-nm Au film. For this measurement we used a Au-coated transparent ZnO wafer which was prepared simultaneously with the Ge samples. In the spectral range of 440–600 nm with about 70% of the total luminous intensity, one can estimate the transmission to be in the range of 28–39%16 with a peak at 500 nm. The higher measured transmission indicates that the real thickness of the Au film is ~15 nm.
The μSR signal in Ge at a mean depth of 85 nm is shown in Fig. 2a. The asymmetry spectrum at 220 K after cooling from room temperature without illumination shows precession of the weakly depolarizing diamagnetic Mu signal with amplitude AD. Under illumination the precession signals exhibit two components at 220 K (Fig. 2b): a fast depolarizing with ~70% of AD and a slow component with a fraction of ~30%. The asymmetry spectra are well fitted19 with the following functions:


where  is the asymmetry of the of muons in the MuT− state at the tetrahedral interstitial site and
is the asymmetry of the of muons in the MuT− state at the tetrahedral interstitial site and  is the asymmetry of muons in the
is the asymmetry of muons in the  state at a bond center site between two Ge host atoms: the T and the BC sites are the two crystallographic positions of Mu in Ge17,18. Without light and at T > 280 K, both states are indistinguishable and have nearly the same “slow” depolarization rate Λs and the “slow” asymmetry
state at a bond center site between two Ge host atoms: the T and the BC sites are the two crystallographic positions of Mu in Ge17,18. Without light and at T > 280 K, both states are indistinguishable and have nearly the same “slow” depolarization rate Λs and the “slow” asymmetry  is the sum of the asymmetries at the two different sites. ϕ is the angle of the muon spin at t = 0 with respect to the positron detector. Under illumination the appearing “fast” component with depolarization rate Λf is attributed to reactions of photo-generated holes with the MuT− state. By comparison with previous bulk μSR studies of photoexcited Ge18, which show analogous signals, the two components of equation (2) are believed to be a consequence of the following two reactions: i)
is the sum of the asymmetries at the two different sites. ϕ is the angle of the muon spin at t = 0 with respect to the positron detector. Under illumination the appearing “fast” component with depolarization rate Λf is attributed to reactions of photo-generated holes with the MuT− state. By comparison with previous bulk μSR studies of photoexcited Ge18, which show analogous signals, the two components of equation (2) are believed to be a consequence of the following two reactions: i)  and ii),
and ii),  , where electron (e−) or hole (h+) capture, respectively, lead to neutralization of the corresponding diamgnetic state, i.e. conversion to the paramagnetic neutral state. Thermal activation is responsible for the reverse reactions. For i) the reverse reaction is expected to be much faster at 220 K (thousands of MHz) than the carrier capture rate and the hyperfine frequency of
, where electron (e−) or hole (h+) capture, respectively, lead to neutralization of the corresponding diamgnetic state, i.e. conversion to the paramagnetic neutral state. Thermal activation is responsible for the reverse reactions. For i) the reverse reaction is expected to be much faster at 220 K (thousands of MHz) than the carrier capture rate and the hyperfine frequency of  (~100 MHz), see Methods. These rates imply that the loss of muon spin coherence is negligible while the muon is in the paramagnetic state, resulting in a slow depolarization of the
(~100 MHz), see Methods. These rates imply that the loss of muon spin coherence is negligible while the muon is in the paramagnetic state, resulting in a slow depolarization of the  signal (ABC+). For ii), on the contrary, the ionization rate at 220 K is of the order of the hyperfine frequency of
signal (ABC+). For ii), on the contrary, the ionization rate at 220 K is of the order of the hyperfine frequency of  (2360 MHz). In this case, hole capture of Mu− is competing with thermal activation, causing a significant loss of coherence in the Mu− precession signal (AT−), see Methods. Furthermore, the fast rate Λf can be used as a measure of the free hole concentration p:
(2360 MHz). In this case, hole capture of Mu− is competing with thermal activation, causing a significant loss of coherence in the Mu− precession signal (AT−), see Methods. Furthermore, the fast rate Λf can be used as a measure of the free hole concentration p:  10, where
10, where  is the hole capture rate, vp is the hole velocity and
is the hole capture rate, vp is the hole velocity and  is the hole capture cross section of Mu−.
is the hole capture cross section of Mu−.
Germanium (100), 0.1 T applied field, implantation energy 14.1 keV, mean depth <z> = 85 nm.
(a), μSR asymmetry AD at 220 K, in the dark, MTI sample. The solid line is a fit of equation (1) to the data. For better illustration data are shown in a rotating reference frame (rrf) of 11.5 MHz. (b), AD after one hour illumination with blue LEDs (λ = 405 nm, ~8 mW/cm2), rrf representation. A fast depolarizing component is visible in the first 3 μs and a much slower component at later times. The solid line is a fit of equation (2) to the data. (c), The depolarization rates Λs and Λf of the slow and fast components as a function of temperature T and history for two different commercial wafers (CrysTec GmbH and MTI corporation). The Λs data are beneath the red dashed line, Λf data are above. Λf is proportional to the hole concentration p. Samples are cooled in the dark to 220 K (1), followed by illumination at 220 K for a period indicated in the legend (2) and measured after turning the light off (3). The fast component persists indicating the presence of free holes. After warming above 280 K the fast component disappears. The time of the warming sequence (light off) varied between 4 h (closed squares), 9 h (closed circles and triangles) and 19 h (open circles).
The behavior of Λf ∝ p and Λs as a function of temperature, illumination and history, shown in Fig. 2c, constitutes the main findings of this work. On lowering the temperature from 290 K without illumination the depolarization rate Λs slowly decreases, as is typically observed for low doped n-type Ge10,18. In this case the asymmetry spectra are fit by a single “slow” component, where Λs is caused by cyclic charge state transitions involving conduction electrons (but not holes)17 and by nuclear magnetic dipolar fields of the 73Ge isotope. Turning on the light at 220 K leads to the appearance of the “fast” component. Illumination with white light of intensity 10 mW/cm2 for about 5 h saturates the depolarization rate Λf to a value of ~17 μs−1. Using blue light (λ = 470 nm) at the same intensity the saturation occurs earlier (after 2 h). The saturation value of Λf, which is proportional to the photo-induced hole concentration, can be further increased by using shorter wavelength light of 405 nm and increased intensity of 80 mW/cm2, where saturation is already obtained after 35 min. From Λf ~ 40 μs−1 we estimate a hole concentration of ~1.6 × 1014/cm3, see Methods. The most intriguing result is the persistence of the “fast” component. For example, after the light is turned off at 220 K for ~12 h, Λf decreases only to 50% of its value directly after illumination, see Fig. 3a. The persistence can be explained by trapping of photo-generated electrons in empty surface states (see Discussion): the negative charging of the surface inverts the surface region from n-type to p-type through accumulation of excess free holes. It is only after warming the samples to 280 K that the fast component quickly disappears and only a single “slow” component (Λs) remains. This indicates that a thermally activated process liberates the electrons from the surface states, thus leading to recombination with the free holes and a “resetting” of the sample to its original state. In the temperature range between 270 K and 280 K Λf, i.e. the hole carrier concentration, quickly disappears. An Arrhenius plot of Λf in this temperature range allows to estimate an activation energy of 1.1 ± 0.3 eV for this process, see Fig. 3b. The error is the standard deviation of the fitted value of the activation energy. The much slower decrease of Λf between 220 K and 270 K is caused by the thermally activated increase of the MuT− formation rate (ionization of  ), so that the muon spends less and less time in the depolarizing
), so that the muon spends less and less time in the depolarizing  state when the temperature is raised, see Methods.
state when the temperature is raised, see Methods.
Germanium (100), fast depolarization rate Λf, CrysTec sample.
(a), Λf at temperature T = 220 K as a function of time after terminating the illumination with white LEDs at 10 mW/cm2 for 5 h. The solid line is a fit of the exponential function exp(−t/τD), where t is the time and τD the time constant of the decrease of Λf. The fit yields τD = 16.7 ± 5.5 h, which corresponds to a half-life of about 12 h. The error indicates the standard deviation of the fit result. (b), Arrhenius plot of Λf between 270 K and 280 K. Fit function is Λf(T) = C exp(EA/kBT), where C is a constant, EA = 1.1 ± 0.3 eV is the activation energy and kB is the Boltzmann constant.
The whole cycle described above is reproducible. This photo-induced persistent change of charge carrier concentration is very well reproduced in complementary resistance measurements, see Fig. 4. We also measured Λf as a function of implantation energy between 4 and 25 keV, corresponding to mean/maximum depths of 25/50 nm and 155/210 nm and found no depth dependence. This indicates that the hole concentration does not change at least up to a depth of ~200 nm. This can be explained by the expected thickness of the accumulation layer for a carrier concentration of ~1014/cm3, which is in the order of one micrometer, see Methods. In bulk μSR studies on Ge and Si no persistent photo-induced effects have been reported18,22,23,24.
Germanium (100), MTI sample, resistance measurements.
(a), resistance R as a function of time during cooling from 300 K to 130 K. Light is turned on at ~12200 s, λ = 405 nm, 80 mW/cm2. The drop of resistance is caused by the photogenerated charge carriers. After switching off the light at ~14600 s the resistance doesn't return to its initial value R0, but only to ~0.5 R0, which is clear evidence for a persistent charge carrier accumulation in the sample. The slow increase of R as a function of time indicates the slow recombination of electrons trapped at the surface with accumulated holes close to the surface. At ~18300 s a slow warmup of the sample to 300 K is initiated. (b), R as a function of temperature T. The sample was cooled in the dark to various temperatures and illuminated for 1 h at that temperature, followed by a wait (“relaxation”) for 1 h in the dark and a slow warmup to 300 K. The cooling and warming-after-illumination curves merge between 260 and 280 K, which matches exactly the temperature range where the μSR data show the thermally activated recombination of surface electrons with accumulated holes near the surface.
Discussion
An explanation for the trapping of photo-generated electrons at the surface is provided by a model which assumes the presence of surface acceptor states located close to the valence band edge in Ge. These states - dangling bonds or other defects - can be easily filled, building a negative surface charge which drives the surface to inversion20,21. The ease of inversion appears to be an intrinsic property of Ge surfaces, as confirmed by our present observation of inversion in wafers from different suppliers. The model is further supported by our investigations of n-type samples with higher doping levels of n ~ 4 × 1014 /cm3 and n ~ 5 × 1017 /cm3. Whereas the first sample shows persistent inversion, no light-induced effects are observed for the latter. This appears to be reasonable for the sample with n ~ 5 × 1017 /cm3 since the free electron concentration by doping is at least two orders of magnitude larger than the photo-induced carrier concentration, resulting in a rapid recombination of the photo-generated holes. On the other hand, one can expect that photo-generated electrons are still trapped in the surface acceptor states, so that the negative surface charge still could generate an accumulation of holes and a depletion of electrons at the surface. According to the model of Refs. 20, 21 this is inhibited for doping levels of  , in agreement with our data. It can be explained by the position of the Fermi level at the surface: for
, in agreement with our data. It can be explained by the position of the Fermi level at the surface: for  the level is above the surface acceptor states causing these states to be filled with electrons. Therefore, photo-induced electrons can't be trapped anymore at the surface in this case. Photo-induced inversion is also destroyed by building a Schottky-barrier at the surface. After sputtering a 20-nm-thin Au layer on top of the Ge samples – thin enough to enable 40–50% of white light to penetrate the Au film – we did not observe any photo-induced change of the depolarization rate: the data are well fitted by a single “slow” component, equation (1) and the depolarization rates Λs agree with the “no light” data in Fig. 2c. This means that photo-induced hole accumulation at the Au/Ge interface is completely suppressed. Strong band bending at the interface probably causes a fast separation/depletion of photo-generated charge carriers from the region where the muons are stopping, inhibiting hole accumulation at the interface. This further supports the interpretation that charge accumulation at the Ge surface is driving the inversion.
the level is above the surface acceptor states causing these states to be filled with electrons. Therefore, photo-induced electrons can't be trapped anymore at the surface in this case. Photo-induced inversion is also destroyed by building a Schottky-barrier at the surface. After sputtering a 20-nm-thin Au layer on top of the Ge samples – thin enough to enable 40–50% of white light to penetrate the Au film – we did not observe any photo-induced change of the depolarization rate: the data are well fitted by a single “slow” component, equation (1) and the depolarization rates Λs agree with the “no light” data in Fig. 2c. This means that photo-induced hole accumulation at the Au/Ge interface is completely suppressed. Strong band bending at the interface probably causes a fast separation/depletion of photo-generated charge carriers from the region where the muons are stopping, inhibiting hole accumulation at the interface. This further supports the interpretation that charge accumulation at the Ge surface is driving the inversion.
In summary we have shown that a semiconductor surface can be persistently inverted by photo-excitation, very similar to charge accumulation in a near-surface layer in electric field transistors. It is conceivable that – by proper tailoring of the surface – charge carrier concentrations can be manipulated over a larger range than presented in this work, which is potentially interesting for future applications in opto-electronic devices.
Methods
Used light sources
For the 33 commercial LEDs mounted in series on a ring inside the radiation shield two types of LEDs were used: white (Avago HLMP-CW36-UX00, peak wavelengths at 460 nm and 560 nm) and blue (Kingbright L-7113QBC-D) with a peak wavelength of 470 nm and spectral line full-width-at-half-maximum (FWHM) of 50 nm. The maximum current/voltage rating at room temperature is 30 mA/3.3 V. The viewing angles are 2Θ1/2 = 30° for the white and 2Θ1/2 = 16° for the blue LEDs, where Θ1/2 is the angle with respect to the optical center line where the luminous intensity is 1/2 of the center line value, i.e. the light is emitted in forward direction in a narrow cone. The maximum intensity at the sample for this setup is 10 mW/cm2. For higher intensities up to 80 mW/cm2 a LED point source with four LEDs (bluepoint LED by Hönle UV technology, 405 nm peak wave length, spectral width 9 nm FWHM) is installed 1.9 m upstream of the sample outside the vacuum chamber. The light is focussed by two optical lenses through a vacuum viewport onto the sample.
Ionization, charge capture and carrier concentrations
Thermal activation or ionization of Mu impurities is usually described by an Arrhenius process with the ionization rate Λi = Λ0 exp(−EA/kT), where Λ0 is the “attempt” frequency and EA the activation energy17. For  in Ge EA ~ 145 meV25 and Λ0 = 2.9 × 1013 /s17. It follows Λi ~ 14000 MHz at 220 K. The electron capture rate
in Ge EA ~ 145 meV25 and Λ0 = 2.9 × 1013 /s17. It follows Λi ~ 14000 MHz at 220 K. The electron capture rate  MHz is much smaller. Here,
MHz is much smaller. Here,  cm2 is the electron capture cross section17, vn = 2.7 × 107 cm/s is the electron velocity in Ge at 220 K26 and n = 3 × 1013 cm−3 is the electron density in the dark. A necessary condition to avoid loss of spin coherence in the precession of diamagnetic
cm2 is the electron capture cross section17, vn = 2.7 × 107 cm/s is the electron velocity in Ge at 220 K26 and n = 3 × 1013 cm−3 is the electron density in the dark. A necessary condition to avoid loss of spin coherence in the precession of diamagnetic  – if it forms from a paramagnetic
– if it forms from a paramagnetic  precursor – is that
precursor – is that  , where
, where  MHz is the hyperfine coupling of
MHz is the hyperfine coupling of  10. In this case, the lifetime of the neutral state is short enough to ensure that the muon spin precession due to the hyperfine field of the electron can be neglected. Even if there is a sizeable electron capture rate of
10. In this case, the lifetime of the neutral state is short enough to ensure that the muon spin precession due to the hyperfine field of the electron can be neglected. Even if there is a sizeable electron capture rate of  , as it is the case here, ionization of
, as it is the case here, ionization of  is sufficiently fast to avoid loss of polarization, i.e. the depolarization rate of the
is sufficiently fast to avoid loss of polarization, i.e. the depolarization rate of the  signal is small.
signal is small.
For  with EA ~ 170 meV, the corresponding ionization rate Λi ~ 3700 MHz at 220 K is of the order of the hyperfine coupling
with EA ~ 170 meV, the corresponding ionization rate Λi ~ 3700 MHz at 220 K is of the order of the hyperfine coupling  MHz of
MHz of  10. Hole capture of
10. Hole capture of  causes therefore a temporal loss of polarization which leads to the observed Λf ~ 40 μs−1 at 220 K. Using a Monte-Carlo simulation27 of cyclic charge state transitions between
causes therefore a temporal loss of polarization which leads to the observed Λf ~ 40 μs−1 at 220 K. Using a Monte-Carlo simulation27 of cyclic charge state transitions between  and
and  states we find that a hole capture rate of
states we find that a hole capture rate of  MHz at 220 K is required to obtain the experimentally observed Λf, i.e.
MHz at 220 K is required to obtain the experimentally observed Λf, i.e.  with
with  . Knowing
. Knowing  we can estimate the photo-induced hole concentration p by using the value of
we can estimate the photo-induced hole concentration p by using the value of  from the simulation and the known hole velocity vp in Ge26. We derived the hole capture cross section
from the simulation and the known hole velocity vp in Ge26. We derived the hole capture cross section  from bulk μSR data (measured at the GPS instrument at PSI, indicated in the following by the superscript b) of a p-type Ge sample with
from bulk μSR data (measured at the GPS instrument at PSI, indicated in the following by the superscript b) of a p-type Ge sample with  cm−3. In this experiment we measured
cm−3. In this experiment we measured  between 250 K and 290 K. The observed
between 250 K and 290 K. The observed  can be well reproduced by the simulation assuming
can be well reproduced by the simulation assuming  MHz at 220 K. We obtain
MHz at 220 K. We obtain  cm2, where we used vp = 1.6 × 107 cm/s at 220 K26. Using this value of
cm2, where we used vp = 1.6 × 107 cm/s at 220 K26. Using this value of  we can estimate the photo-induced hole concentration to
we can estimate the photo-induced hole concentration to  .
.
The simulation also shows that Λf is decreasing as a function of temperature because of the exponentially increasing Λi, in good agreement with the observed decrease of Λf between 220 K and 265 K. Note, that  is also expected to increase with temperatur T, because of
is also expected to increase with temperatur T, because of  26. An increase of
26. An increase of  should cause an increase of Λf. However, Λi changes exponentially with T and dominates the dynamics of the
should cause an increase of Λf. However, Λi changes exponentially with T and dominates the dynamics of the  charge cycles. The much faster decrease of Λf between 270 K and 280 K can not be explained by this model which assumes charge cycles due to the presence of holes. The disappearance of holes in this temperature range – by recombination with electrons liberated from the surface states – stops the
charge cycles. The much faster decrease of Λf between 270 K and 280 K can not be explained by this model which assumes charge cycles due to the presence of holes. The disappearance of holes in this temperature range – by recombination with electrons liberated from the surface states – stops the  charge cycles, which explains the fast drop of Λf.
charge cycles, which explains the fast drop of Λf.
The photo-induced hole carrier concentration can be independently estimated by the change of resistance R after illumination. The measurements in Fig. 4 yield a persistent reduction of R by a factor 2–3. The initial resistivity ρ at room temperature of 50–60 Ωcm corresponds to  28. After illumination, ρ ~ 20–25 Ωcm and assuming that the conductivity is now p-type we can estimate the hole carrier concentration to be
28. After illumination, ρ ~ 20–25 Ωcm and assuming that the conductivity is now p-type we can estimate the hole carrier concentration to be  28, in excellent agreement with the μSR data.
28, in excellent agreement with the μSR data.
Thickness of hole accumulation layer
The thickness d of the hole accumulation layer can be estimated by  1, where εr = 16 is the dielectric constant of Ge, ε0 is the permittivity of free space, U is the surface potential, e the electron charge and p the hole concentration. Assuming that the surface potential U is close to the charge neutrality level at the Ge surface21 we use U ~ 0.3 V to obtain d = 1.8 μm for p = 1.6 × 1014 /cm3.
1, where εr = 16 is the dielectric constant of Ge, ε0 is the permittivity of free space, U is the surface potential, e the electron charge and p the hole concentration. Assuming that the surface potential U is close to the charge neutrality level at the Ge surface21 we use U ~ 0.3 V to obtain d = 1.8 μm for p = 1.6 × 1014 /cm3.
References
Sze, S. M. & Ng Kwok, K. Physics of Semiconductor Devices - Third Edition (John Wiley & Sons, Hoboken, New Jersey, 2007).
Colinge, J.-P. et al. Nanowire transistors without junctions. Nature Nanotech. 5, 225–229 (2010).
King, P. D. C. et al. Surface Electron Accumulation and the Charge Neutrality Level in In2O3 . Phys. Rev. Lett. 101, 116808 (2008).
Freijlich, J., Longeuad, C. & Carvalho, J. F. Photoinduced Schottky Barrier in Photorefractive Materials. Phys. Rev. Lett. 104, 116601 (2010).
Lin, C.-H., Chen, T.-T. & Chen, Y.-F. Photocurrent enhancement of SnO2 nanowires through Au-nanoparticles decoration. Optics Express, 16, 16916 (2008).
Alexe, M. Local Mapping of Generation and Recombination Lifetime in BiFeO3 Single Crystals by Scanning Probe Photoinduced Transient Spectroscopy. Nano Lett. 12, 2193 (2012).
Takihara, M., Takahashi, T. & Ujihara, T. Minority carrier lifetime in polycristalline silicon solar cells studied by photoassisted Kelvin probe force microscopy. App. Phys. Lett. 93, 021902 (2008).
Coffey, D. C. & Ginger, D. S. Time-resolved electrostatic force microscopy of polymer solar cells. Nature Mater. 5, 735 (2006).
Yaouanc, A. & Dalmas de Réotier, P. Muon Spin Rotation, Relaxation and Resonance – Applications to Condensed Matter (Oxford University Press, Oxford, 2011).
Patterson, B. D. Muonium states in semiconductors. Rev. Mod. Phys. 60, 69–159 (1988).
Chow, K. H., Hitti, B. & Kiefl, R. F. μSR on Muonium in Semiconductors and Its Relation to Hydrogen. Semiconductors and Semimetals Vol. 51A, edited by Stavola, M. 137–207 (Academic Press, San Diego and London, 1998).
Cox, S. F. J. Muonium as a model for interstitial hydrogen in the semiconducting and semimetallic elements. Rep. Prog. Phys. 72, 116501, 1–130 (2009).
Prokscha, T. et al. The new μE4 beam at PSI: A hybrid-large acceptance channel for the generation of a high intensity surface-muon beam. Nucl. Instr. Meth. A 595, 317–331 (2008).
Morenzoni, E. et al. Generation of very slow polarized positive muons. Physical Review Letters 72, 2793 (1994).
Prokscha, T. et al. Low-energy μSR investigations of photo-induced effects on a nm scale. Physics Procedia 30, 219–223 (2012).
Johnson, P. B. & Christy, R. W. Optical Constants of Noble Metals. Physical Review B 6, 4370–4379 (1972).
Lichti, R. L. et al. Charge-state transitions of muonium in germanium. Phys. Rev. B 60, 1734–1745 (1999).
Fan, I. et al. Influence of photoexcitation on the diamagnetic muonium states in Ge studied via their precession signatures. Phys. Rev. B 78, 153203 (2008).
Suter, A. & Wojek, B. M. Musrfit: A Free Platform-Independent Framework for μSR Data Analysis. Physics Procedia 30, 69 (2012).
Tsipas, P. & Dimoulas, A. Modeling of negatively charges states at the Ge surface and interfaces. Appl. Phys. Lett. 94, 012114 (2009).
Dimoulas, A. & Tsipas, P. Germanium surface and interfaces. Microelectronic Engineering 86, 1577 (2009).
Fan, I. et al. Optically induced dynamics of muonium centers in Si studied via their precession signatures. Phys. Rev. B 77, 035203 (2008).
Kadono, R., Matsuhsita, A., Macrae, R. M., Nishiyama, K. & Nagamine, K. Muonium Centers in Crystalline Si and Ge under Illumination. Phys. Rev. Lett. 73, 2723–2727 (1994).
Kadono, R., Macrae, R. M., Nishiyama, K. & Nagamine, K. Evidence for muonium passivation in n-doped Ge. Phys. Rev. B 55, 4035–4038 (1997).
Lichti, R. L., Chow, K. H. & Cox, S. F. J. Hydrogen Defect-Level Pinning in Semiconductors: The Muonium Equivalent. Phys. Rev. Lett. 101, 136403 (2008).
Ioffe Physical Technical Institute. Electrical properties of Germanium (Ge). Available at: http://www.ioffe.ru/SVA/NSM/Semicond/Ge/electric.html [Accessed 19th December 2012]. The thermal velocity scales with which allows to extrapolate to velocities at 220 K.
Prokscha, T. Monte-Carlo Simulation of Transitions between Different Muonium States. Physics Procedia 30, 50 (2012).
Cuttriss, D. B. Relation between Surface Concentration and Average Conductivity in Diffused Layers of Germanium. Bell System Technical Journal, 509 (1961).
Eckstein, D. Computer Simulation of Ion-Solid Interactions. (Springer, Berlin, Heidelberg, New York, 1991).
Morenzoni, E. et al. Implantation studies of keV positive muons in thin metallic layers. Nucl. Instr. Meth. B 192, 254 (2002).
Philipp, H. P. & Taft, E. A. Optical Constants of Germanium in the Region 1 to 10 eV. Physical Review 113, 1002–1005 (1959).
Acknowledgements
We thank M. Horisberger for sputtering the Au films and H.P. Weber for his excellent technical support.
Author information
Authors and Affiliations
Contributions
T.P., K.H.C. and R.S. proposed the present study. T.P. organized the research project. T.P., A.S., H.L., E.M., G.J.N. and Z.S. contributed to the development and maintenance of the low-energy μSR setup. T.P., K.H.C., E.S., H.L., G.J.N. and R.S. were involved in the μSR experiments. E.S. and A.S. performed the resistance measurements. T.P. performed data analysis and drafting of the text. T.P., K.H.C., E.S., A.S., H.L., E.M., Z.S. and R.S. contributed to revisions of the text.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Rights and permissions
This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivs 3.0 Unported License. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-nd/3.0/
About this article
Cite this article
Prokscha, T., Chow, K., Stilp, E. et al. Photo-induced persistent inversion of germanium in a 200-nm-deep surface region. Sci Rep 3, 2569 (2013). https://doi.org/10.1038/srep02569
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep02569
This article is cited by
-
A segmented conical electric lens for optimization of the beam spot of the low-energy muon facility at PSI: a Geant4 simulation analysis
Nuclear Science and Techniques (2017)
-
Controlling the near-surface superfluid density in underdoped YBa2Cu3O6+x by photo-illumination
Scientific Reports (2014)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.