Abstract
Water in the xylem, the water transport system of plants, is vulnerable to freezing and cavitation, i.e. to phase change from liquid to ice or gaseous phase. The former is a threat in cold and the latter in dry environmental conditions. Here we show that a small xylem conduit diameter, which has previously been shown to be associated with lower cavitation pressure thus making a plant more drought resistant, is also associated with a decrease in the temperature required for ice nucleation in the xylem. Thus the susceptibility of freezing and cavitation are linked together in the xylem of plants. We explain this linkage by the regulation of the sizes of the nuclei catalysing freezing and drought cavitation. Our results offer better understanding of the similarities of adaption of plants to cold and drought stress and offer new insights into the ability of plants to adapt to the changing environment.
Similar content being viewed by others
Introduction
In a changing climate, plants will meet new environmental conditions such as different regional temperature and precipitation patterns. These changes will affect the probability of freezing and cavitation1, i.e. phase change of liquid water to ice or gas, respectively, in the xylem of pants. Freezing and cavitation form a risk for tree function and survival because water conductance inside trees scales with photosynthesis and growth2, but water conductance is only possible in liquid form. Cavitation has been recognized as one of the key factors leading to reduced plant productivity and mortality during drought3 and factors influencing the vulnerability of the xylem to cavitation have been studied extensively4. It is known that there is a relation between the critical pressure causing cavitation during drought and anatomical plant characteristics5,6,7, although the causality has not been satisfactory shown. However, the critical temperature causing ice nucleation in the water transport system8,9,10 has not been given much consideration.
Liquid water is vulnerable to phase change into ice at sub-zero temperatures, similarly as it is into vapour at liquid pressures below its saturation vapour pressure11. The ecological significance of the freezing temperature of the xylem to plant productivity and survival worldwide is likely less important in comparison to that of cavitation. However, the factors influencing freezing could be important for plant function and survival in colder environments12,13. Ice nucleation temperature in xylem conduits, the dead cells responsible for transporting water from the roots to the foliage, determines the frozen time period and the number of freeze-thaw cycles a tree experience during winter. Short frozen period and low number of freeze-thaw cycles have a positive effect on tree function and survival because as long as water in the xylem is not frozen, there is no risk for typical freezing damages that are especially enhanced by continuous freeze-thaw cycles. Typical freezing damages in trees adapted to colder environments include bubble formation during freezing and thawing causing winter cavitation and further blockages in water transport14 and dehydration of unfrozen living cells due to low water potential of extracellular ice as water potential over ice decreases approximately 1.2 MPa per 1°C decrease in ice temperature15,16. Low ice nucleation temperature also makes it possible for an evergreen tree to photosynthesize on sunny days even when the ambient temperature is below zero17 which will make them effective carbon sinks18 and aerosol sources19. In milder regions, high freezing temperature of xylem water can be beneficial for trees as it protects the living cells by providing temporary cold protection with released heat of fusion20. Also in colder regions, too low ice nucleation temperature could be harmful for trees. Lower freezing temperature increases the risk of intracellular freezing of the living cells as dehydration of the living cells due to the extracellular ice increases their osmotic concentration21 and may allow them to tolerate very low freezing temperatures22.
Liquid water is transported in xylem conduits (Fig. 1) under negative pressures according to the cohesion-tension mechanism23,24 allowed by strong inter-molecular attraction. Negative pressure, i.e. large water tension (see Fig. 2), is created as evaporation at the leaf surfaces pulls water columns, held together by cohesive forces, upwards from the soil through the xylem. Water tension inside the xylem increases with decreasing soil water availability and increasing transpiration rate. At sub-zero temperatures, liquid water is also prone to freezing as the vapour pressure over ice is lower than that over liquid water (see Fig. 2). In these conditions, water inside the xylem is in a unique thermodynamic state in the sense that it is metastable to two directions: it is simultaneously supercooled, i.e. temperature of liquid water is below the equilibrium ice nucleation temperature and under tension, i.e. pressure of liquid water is below the saturation vapour pressure11.
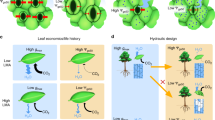
Schematic presentation of conduits of a deciduous tree species and inter-conduit pits (a) between two water-filled conduits and (b) between a gas-filled and a water-filled conduit.
In (a), impurities and other solid particles can enter a conduit through a pit membrane in the case of large enough pores and become potential ice nuclei. In (b), gas penetrates from a gas-filled conduit to adjacent water-filled conduit through a pit membrane in the case of large enough pores and induces cavitation.
Water can remain in its metastable liquid state as long as there are no solid impurities or gas phases (bubbles or menisci) of large enough size present to act as nuclei and catalyse the formation of a new phase, i.e. ice or gas. Homogeneous ice nucleation of water takes place at approximately −40°C11 and homogeneous cavitation of water at approximately −100 MPa11, which is far below the pressures found in any plants. Heterogeneous ice nucleation at warmer temperatures or cavitation at higher pressures requires the presence of nuclei of sufficient surface properties, geometry and size25. Here we investigate how an important characteristic of xylem anatomy, its conduit diameter, regulates the sizes of nuclei catalysing freezing inside trees and how this regulation determines the environmental conditions critical for the phase transition into ice. We then compare the sensitivity of ice nucleation temperature on xylem conduit diameter to the previously well-known relationship of cavitation pressure sensitivity on xylem conduit diameter.
Results
We found that the ice nucleation temperature of water in the xylem increased with increasing conduit size regardless of the species or tree part (Fig. 3A). There is no known direct causality that would explain the found relationship. We thus hypothesize that the relationship between ice nucleation temperature and conduit radius can be explained from the basis of the classical nucleation theory and the scaling relations between conduit, pore and nucleus radius. Our theoretical calculation using the classical nucleation theory demonstrated that the maximum supercooling temperature, i.e. the reciprocal of ice nucleation temperature, is inversely proportional to the size of a nucleus at the temperature range in which ice nucleation occurs in trees25 (Fig. 3B). The size of the nuclei present in the xylem sap is determined by the inter conduit pit pores that act as filters allowing water and dissolved nutrients to enter the conduits, but constrict the spreading of gas bubbles and solid impurities in excess of few nanometres (see Fig. 1). It has been empirically confirmed that pore sizes in the pit restrict the size of particles which can enter the conduits26,27, so we further obtain an inverse relation between maximum supercooling temperature and pit pore size. Finally, there are two prevailing hypothesis on the linkage between the pit pore size and conduit size: the pit-resistance hypothesis28 of nearly linear scaling between average pore size and conduit size and the rear pit hypothesis5 of nearly linear scaling between the maximum pore size and conduit size. Thus we concluded that the maximum supercooling temperature is approximately inversely proportional to conduit size, because the size of the largest particles that are able to penetrate through the pit pores determines the ice nucleation temperature in the xylem.
(a) Measurements (N = 70) of ice nucleation temperature of water in trees and maximum conduit radius.The narrowest conduits were found in conifers and the widest in deciduous species. Curve for the theoretical relationship is drawn. (b) Theoretical relationship between ice nucleation temperature and ice nucleus radius with varying particle surface properties denoted with θ (equation 5) in the insert. The ice nucleation temperature is calculated to be reached when the nucleation probability exceeds 0.5 in one minute for a sample of 3 cm3 in volume (a cylinder of 1 cm in radius and 1 cm in height).
Figure 4 demonstrates a striking similarity of the relation of ice nucleation temperature to conduit size to the previously known relation of cavitation pressure to conduit size. Both relations are strongly supported by empirical evidence; for ice nucleation from our own results as shown above and for cavitation from earlier studies5,6,7. In our theoretical analysis (see Methods section), we linked the susceptibility to freezing and cavitation with plant anatomical characteristics based on the relation between nucleus size (impurity or gas phase) and the ability to penetrate into the metastable region of temperature or pressure, which are both proportional to the inverse of pit pore size.
Empirical results concerning the relationship between drought cavitation pressure and conduit radius are compared with the theoretical relationship between ice nucleation temperature and conduit radius that is also supported by the empirical data (R2 = 0.35, P < 0.0001).
Drought cavitation is described with the pressure reducing 50% of the hydraulic conductivity (P50). The linear regression line of Wilson and Jackson6 was drawn visually from the original figure. The definition of conduit radius was different in different studies: mean conduit radius5, hydraulically weighted mean radius (Σr5/Σr4)6 and mean radius of conduits responsible for 95% of water flow7 were used. In this study we used maximum conduit radius.
To get a better understanding of the potential significance of ice nucleation temperature in xylem for tree functioning, we made some calculations from weather data measured in Southern Finland (SMEAR II station29 61°51′ N, 24°17′ E). Within a 15-years follow-up period, the time that the xylem was frozen was half shorter and the number of freeze-thaw cycles was only 15% for a tree with ice nucleation temperature of −10°C compared to a tree with ice nucleation temperature of −1°C.
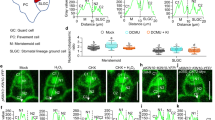
To confirm that the found relationship between conduit radius and ice nucleation temperature was not an artefact caused by the varying sample size and cooling rate30,31,32, we tested the effect of these variables together with conduit radius. Conduit radius increased the freezing temperature highly significantly (p < 0.0001, Fig. 5C), sample volume barely significantly (p = 0.036, Fig. 5A), but there was no effect of cooling rate (p = 0.269, Fig. 5B) on ice nucleation temperature. There was some dependency between conduit radius and sample volume (R = 0.29). This dependency results from the general trend between conduit size and branch/stem diameter33. However, the multicollinearity was not severe and allowed separation of the studied effects in the statistical analysis.
Relationship of ice nucleation temperature with (a) sample volume, (b) cooling rate and (c) maximum conduit radius.
The lines represent statistical prediction between ice nucleation temperature and sample volume (a) and ice nucleation temperature and maximum conduit radius (c) when the effect of other variables in the multivariate model were fixed to data averages. There was no significant dependency between ice nucleation temperature and cooling ratio (b).
We further modified the surface energy of the water-ice nuclei by adding a surfactant to the xylem sap. The addition of the surfactant to water decreased the surface energy of the nuclei and increased the average ice nucleation temperature from the average of −4.3°C (N = 3, s.d. = 0.9) and −4.2°C (N = 3, s.d. = 0.5) to −2.1°C (N = 3, s.d. = 0.5) and −2.5°C (N = 3, s.d. = 0.1) in Pinus sylvestris and Betula pendula, respectively. This result, along with the sharp exotherms associated with the freezing events (Supplementary Fig. S1) and thawing occurring always at the equilibrium ice nucleation temperature around 0°C, demonstrate that the freezing of the xylem sap was not an equilibrium freezing but the xylem sap was supercooled (Fig. 1).
Discussion
We showed that the temperature at which the xylem of a plant freezes is dependent on its anatomical characteristics as conduit size determines the size of the largest particles that are able to penetrate through the pit pores and catalyse ice nucleation. The theoretical size range of solid particles catalysing ice nucleation in the empirically measured temperature range coincides with empirical findings of particle sizes being able to penetrate through pits into conduits in trees26,27. Different sized organic and inorganic nuclei, of either external origin or synthesized by the plant itself, are commonly found in plants and their presence has been shown to affect ice nucleation34; the ice-like structures of nuclei catalyse the organization of water molecules into an ice crystal lattice20. It has also been suggested that conduit walls would act as ice nuclei35,36 and that the properties of conduit walls would correlate with conduit size36. It seems that in the absence of impurities in xylem water, conduit walls can act as ice nuclei but only at considerably lower temperature compared to the ice nucleation temperatures typically found from plants in nature36,37. The surfaces of the conduit walls do not have the sufficient surface properties to induce ice nucleation at such high temperatures as found in the experiments36,37. It is thus much more probable that nuclei catalysing ice nucleation in conduits have similar nature as aerosols in atmospheric ice nucleation in clouds38. Also gas bubbles created by cavitation have been found to be potential ice nucleation sites39.
We further suggest that conduit size links together ice nucleation and drought cavitation via pit pore size. Drought cavitation most commonly develops in trees by spreading of the gas phase from one conduit to another through heterogeneous nucleation40. It has been suggested that the rare largest pit pore in a conduit determines the water tension in which the gas phase enters the conduit from adjacent conduit through inter-conduit pits5,26. This indicates that similar xylem anatomy secures safety in plants growing in either cold or dry environments. There is one difference in the spreading of the gaseous or ice phase following nucleation: inter conduit pit pore size determines spreading of the gaseous phase separately for each conduit, whereas freezing propagates from one conduit to another within a plant organ rather freely following a single ice nucleation event8. However, it has been shown that the extent of supercooling varies between organs within a tree as there can be ice barriers between tree organs9.
Running a surfactant through samples of Pinus sylvestris and Betula pendula branches before freezing decreased the degree of supercooling by approximately 40–50% in both species. Similarly to our results, lowering the surface tension has been found to increase the pressure required for cavitation in both conifers and angiosperms40,41,42.
As ice nucleation is a stochastic phenomenon, both sample volume and exposure time to a given temperature affect ice nucleation probability30,31,32. In our experiments, we settled for varying sample volume and exposure time as the probability for nucleation will in practice increase from values very close to zero to values approaching one in a narrow temperature range (Supplementary Figs. S2, S3). This was also shown empirically as sample volume had a barely significant effect and exposure time had no effect on the ice nucleation temperature (Fig. 5). We also used single measurements instead of averages of several measurements despite of the stochastic nature of nucleation, because theoretical calculations showed that the nucleation probability increases from zero to one in a very narrow range of the nucleus particle diameter (Supplementary Fig. S4), meaning that the largest impurity is practically always expected to act as nucleus for phase transition.
Our results offer better understanding of the anatomical similarities of adaption of plants to cold and drought stress as in global climatic distribution of species, mean conduit diameter has been found to decrease with the probability of both sub-zero temperatures13 and drought43. In cold climates, trees with small conduits have been shown to suffer less from low temperatures and to have superior productivity compared to trees with larger conduits12. Large conduits enable efficient water transport, whereas small conduits are reliable in water transport, i.e. safe from phase transition from liquid to gas or liquid to solid ice. Efficient and safe water transport is essential for plants because the exchange of water and carbon needed for photosynthesis takes place through the same stomata openings on leaf surface; the rate of water transport scales with metabolism rate on whole plant level2.
We conclude that the linkage between ice nucleation temperature and drought cavitation is significant from an evolutionary point of view. Besides the already widely accepted trade-off at the whole tree level44 between efficient water transport and safety from cavitation through conduit size, there also seems to be a trade-off between efficient water transport and low ice nucleation temperature (Fig. 6). The role of conduit anatomy in determining the length of the frozen period and the number of freeze-thaw cycles a tree encounters each winter, offers new insights into the ability of trees to adapt to the changing climate. Boreal trees with low ice nucleation temperature are effective also in climate change point of view decreasing the global warming by being carbon sinks18 and aerosol sources19 also during winter.
Schematic presentation of the relationship between conduit anatomy and the trade-off between water transport safety and efficiency at whole tree level.
Conduit size scales with the degree of metastability the tree can experience before spreading of cavitation or freezing. Different sized conduits are favoured in different environmental conditions.
Methods
Experimental work
We collected 70 samples during March and April from winter acclimated woody species in Southern Finland near Helsinki. The samples represented 9 deciduous species and 5 conifer species (Table 1). Different tree parts including roots, stems and branches were covered among the sample set and sample size thus varied from 0.03 to 1 178 cm3.
The freezing experiments were conducted in a climate chamber (Weiss Umwelttechnik WK11 −340/40) directly after cutting the samples using cooling rates between 0.06 and 2.9°C Min−1. Temperature of the samples was detected at a measuring interval of 10 seconds with thermocouples inserted a few mm inside the sapwood. Ice nucleation releases heat seen as a freezing exotherm (Supplementary Fig. S1).
After the freezing experiment, 100-μm-thick cross-cuts were cut from the samples with a sliding microtome, stained with safranin, rinsed with water and dehydrated in alcohol. In the case of stem samples, a random cut was taken from the two outermost growth rings that typically have the largest cells45. The maximum conduit lumen area of each sample cross-cut was measured with imaging software and the conduit radius calculated assuming the conduits to be circular.
Because of the stochastic nature of ice nucleation, large sample size and long exposure time can be expected to increase the probability of a nucleation event and thus increase the ice nucleation temperature30,31,32. Increasing sample size may increase the ice nucleation temperature also because the likelihood of having an efficient ice nucleator present increases with sample size. To confirm that the found relationship between conduit radius and ice nucleation temperature was not an artefact, we tested the effect of conduit radius on ice nucleation temperature in a multivariate analysis together with the effects of cooling rate and sample volume (measured over bark). The used method was generalized linear modelling (PROC GENMOD, SAS 9.2, SAS Institute Inc.), so the explanatory variables conduit radius and sample volume were transformed with natural logarithm to obtain a linear relationship with ice nucleation temperature.
We made few additional freezing experiments, where we artificially lowered the surface tensions in the xylem sap using a surfactant (Tween 80) and compared the results with control samples in order to see the effect of nuclei surface energy to the ice nucleation temperature. We ran the surfactant solution (0.5 % v/v), which decreases the surface tension of water to 36 Nm−146, through three Pinus sylvestris branch samples and three Betula pendula branch samples for an hour. The sample was connected to a plastic tube and soap solution was poured into the tube from 1.5 meters height in order to create pressure difference large enough to ensure fluent water conduction.
Theoretical analyses
Part I. Effect of particle size on ice nucleation according to classical nucleation theory
The equilibrium ice nucleation temperature is 0°C at atmospheric pressure for pure bulk water and slightly (typically only a few tenths of a degree) lower for the water in the conduits of trees due to dissolved solutes. Below the equilibrium ice nucleation temperature, phase change to ice would allow the water in conduits to fall to a lower, more favourable energy state. However, before the phase change can occur, new surfaces between the new ice phase and liquid phase need to be constructed which requires energy. Change in the free energy (ΔG) of a spherical ice crystal in a phase change from liquid to ice is11,47

where rice is radius of the spherical ice crystal, L is latent heat of fusion (333.55*106 Jm−3 for a temperature of 273.15 K), TE is equilibrium ice nucleation temperature (273.15 K), ΔT is supercooling temperature, i.e. the temperature minus the equilibrium ice nucleation temperature (Fig. 1) and σLI is surface energy between the two phases (0.030 Nm−1)47. The first term on the right side is the bulk energy term and the second is the surface energy term. Phase change to ice will occur only if ΔG is positive. The sign of (ΔG) at a given temperature is dependent on the radius of the ice crystal. Differentiating equation (1) with respect to rice and solving for ΔG = 0 gives the critical radius of the ice crystal rice*

Ice crystals smaller than this are crushed by surface forces, while ice crystals larger than this are able to grow indefinitely. Ice crystals of radius above the critical size are created by thermodynamic fluctuations which have the energy of the order of kT, where k is the Bolzmann constant (k = 1.38 × 10−23 JK−1). The rate (homogeneous nucleation rate, Jhom) at which these ice crystals are created can be predicted by the classical nucleation theory to be11,47

where J0 is a kinetic pre-factor which has been estimated in the following way48

where N is the molecular density of water (3.35 *1022 (molecules cm−3), h is the Planck's constant (6.626 × 10−34 Js) and QD is the activation energy for diffusion in the liquid (2.8*10−23 J per molecule11. In practice, this equation will give a nucleation rate larger than zero only when temperature approaches the homogeneous ice nucleation temperature of water, which is almost −40°C. Ice nucleation in conduits must therefore occur by heterogeneous nucleation

where a is the surface area available for heterogeneous nucleation per unit bulk volume of liquid. For a spherical ice crystal on a convex surface (Supplementary Fig. S5), the geometrical correction factor f to obtained formation energy of critical cluster in the case of heterogeneous nucleation47,49

Where X is the ratio of the radius of the ice nucleus (rparticle) to the critical ice crystal radius (rice*).



where σL, particle is surface energy between liquid and solid particle and σI, particle is surface energy between ice and solid particle.
Nucleation is a stochastic process, so that a nucleation will only have a given probability to occur for given conditions. In other words, a nucleation temperature cannot strictly be defined. The probability that heterogeneous nucleation will occur in a wood volume of V within a time of exposure (t) to a certain temperature is50

Supplementary Figure S2 shows the nucleation probability as a function of temperature for varying exposure times to a given temperature. As the figure demonstrates, the probability for nucleation will in practice increase from values very close to zero to values approaching one in a narrow temperature range (similarly to the case for cavitation by heterogeneous nucleation50). However, experimental evidence points out to a slightly wider spread in nucleation temperatures51.
Re-arranging equation (4), the temperature at which the nucleation (freezing) occurs can be written

Jreq is the nucleation rate which is required for nucleation to occur, here P = 0.5. Jreq can be explicitly written by substituting Jreq for Jhet in equation (6) and rearranging

In the calculation of the ice nucleation temperature (see Fig. 3B) a value of 0.003 m3 (corresponding to a cylinder of 1 cm in radius and 1 cm in height) is used for the volume (V), 60 s is used for the time (t) and 0.5 is used for the nucleation probability (i.e. nucleation has a 50% probably of occurring). However, the values chosen for the parameters in calculating Jreq in equation (7) influenced the predicted ice nucleation temperature only marginally (Supplementary Fig. S3) due to the dominating effect of other terms in equation (6). A value of 10−5 m2 was used for a in equation (4). The value used for a affected the results so marginally that its value could be changed by many orders of magnitude in either direction without a noticeable effect on the result.
Part II. Scaling of conduit size with cavitation pressure and ice nucleation temperature
Gas will penetrate through the pores in the pits when the pressure difference (ΔP = Pg − PL) between the gas (Pg ~ 1 atmosphere) and liquid phase (PL) over the pores in the pit membrane exceeds1

where rpore is pore size.
The supercooling temperature at nucleation, i.e. the reciprocal of the nucleation temperature, calculated from equation (9) is essentially inversely related to size of the solid impurities (Fig. 3B), i.e. we can write

In practice, the result indicates that a particle can act as an ice nucleus only if it is large enough. Given that the maximum size of the particles present inside a conduit is limited by the sizes of pores in the pit membrane, i.e. (rparticle α rpore) and that the largest impurity is expected practically always to be the nucleus (nucleation probability increases from zero to one in a very narrow range of the nucleus particle diameter, see Supplementary Fig. S4 for an example), an inverse relation is obtained between the maximum supercooling temperature and pore size in the pit membrane

In both cases, i.e. in cavitation (equation 9) and ice nucleation (equation 11), the limit of penetration in to the metastable region of pressure/temperature will be approximately proportional to the inverse of pit pore size.
Further, either average28,52 or maximum pit pore size5,26 or both, scale linearly with conduit size at conduit level. The first proposed relation stems from optimizing the carbon usage so that the proportion of resistance in pit pores vs. conduit lumens remains approximately constant28, whereas the second proposed relation stems from statistical possibilities of having large individual pit pores present when the total pore area per conduit is large5. Both of these options could explain the size of the largest particles found inside conduits at tissue level, but we now assume linear scaling between average pit pore size and conduit size following the pit resistance hypothesis28, i.e. we can write

Assuming that conduit conductance is kconduit α rconduit4 and pit pore conductance is kpore α rpore4 7, we get a relation between pore and conduit diameter

Combining equations (7) and (11), we obtain a relation between ice nucleation temperature and conduit size

and a relation between cavitation pressure and conduit size

References
Tyree, M. T. & Sperry, J. S. Vulnerability of xylem to cavitation and embolism. Annu. Rev. Plant Physiol. Plant Mol. Biol. 40, 19–38 (1989).
West, G. B., Brown, J. H. & Enquist, B. J. A general model for the origin of allometric scaling laws in biology. Science 276, 122–126 (1997).
McDowell, N. et al. Mechanisms of plant survival and mortality during drought: why do some plants survive while others succumb to drought? New Phytol. 178, 719–739 (2008).
Choat, B. et al. Global convergence in the vulnerability of forests to drought. Nature 491, 752–755 (2012).
Wheeler, J. K., Sperry, J. S., Hacke, U. G. & Hoang, N. Inter-vessel pitting and cavitation in woody Rosaceae and other vesselled plants: a basis for a safety versus efficiency trade-off in xylem transport. Plant Cell Environ. 28, 800–812 (2005).
Wilson, C. J. & Jackson, R. B. Xylem cavitation caused by drought and freezing stress in four co-occuring Juniperus species. Physiol. Plant. 127, 374–382 (2006).
Tyree, M. T., Davis, S. D. & Cochard, H. Biophysical perspectives of xylem evolution: is there a tradeoff of hydraulic efficiency for vulnerability to dysfunction? IAWA J. 15, 335–360 (1994).
Hacker, J. & Neuner, G. Ice propagation in plants visualized at the tissue level by infrared differential thermal analysis (IDTA). Tree Physiol. 27, 1661–1670 (2007).
Hacker, J. & Neuner, G. Ice propagation in dehardened alpine plant species studied by infrared differential thermal analysis (IDTA). Arct. Antarct. Alp. Res. 40, 660–670 (2008).
Pramsohler, M., Hacker, J. & Neuner, G. Freezing pattern and frost-killing temperature of apple (Malus domestica) wood under controlled conditions and in nature. Tree Phys. 00, 1–10 (2012).
Debenedetti, P. G. Metastable Liquids: Concepts and Principles (Princeton Univ. Press, 1996).
Schreiber, S. G., Hamann, A., Hacke, U. G. & Thomas, B. R. Sixteen years of winter-stress: an assessment of cold hardiness, growth performance and survival of hybrid poplar clones at a boreal planting site. Plant Cell Environ. 10.1111/j.1365–3040.2012.02583.x (2012).
Noshiro, S. & Baas, P. Systematic wood anatomy of Cornaceae and allies. IAWA J. 19, 43–97 (1998).
Sperry, J. S. & Sullivan, J. E. M. Xylem embolism in response to freeze-thaw cycles and water stress in ring-porous, diffuse-porous and conifer species. Plant Physiol. 100, 605–613 (1992).
Rajashekar, C. B. & Burke, M. J. Liquid water during slow freezing based on cell water relation and limited experimental testing in Plant cold hardiness and freezing stress. (eds Li, P. H. & Sakai, A.) 221–220 (Academic Press 1982).
Washburn, E. W. & West, C. J. International critical tables of numerical data, physics, chemistry and technology (McGraw-Hill 1928).
Sevanto, S. et al. Wintertime photosynthesis and water uptake in a boreal forest. Tree Physiol. 26, 749–757 (2006).
Dunn, A. L., Barford, C. C., Wofsy, S. C., Goulden, M. L. & Daube, B. C. A long-term record of carbon exchange in a boreal black spruce forest: means, responses to interannual variability and decadal trends. Global Change Biol. 13, 577–590 (2007).
Kulmala, M. et al. A new feedback mechanism linking forests, aerosols and climate. Atmos. Chem. Phys. 4, 557–562 (2004).
Zachariassen, K. E. & Kristiansen, E. Ice nucleation and anti-nucleation in nature. Cryobiol. 41, 257–279 (2000).
Burke, M. J., Gusta, L. V., Quamme, H. A., Weiser, C. J. & Li, P. H. Freezing and injury in plants. Annu. Rev. Plant Physiol. 27, 507–528 (1976).
Sakai, A. & Larcher, W. Frost survival of plants: Responses and adaptations to freezing stress (Springer 1987).
Dixon, H. & Joly, J. On the ascent of sap. Ann. Bot. 8, 468–470 (1894).
Pockman, W. T., Sperry, J. S. & O'Leary, J. W. Sustained and significant negative water pressure in xylem. Nature 378, 715–716 (1995).
Fletcher, N. H. Size effect in heterogeneous nucleation. J. Chem. Phys. 29, 572–576 (1958).
Choat, B., Ball, M., Luly, J. & Holtum, J. Pit membrane porosity and water stress-induced cavitation in four co-existing dry rainforest tree species. Plant Physiol. 131, 41–48 (2003).
Wisniewski, M., Ashworth, E. & Schaffer, K. The use of lanthanum to characterize cell wall permeability in relation to deep supercooling and extracellular freezing in woody plants. Protoplasma 139, 105–116 (1987).
Hölttä, T., Mencuccini, M. & Nikinmaa, E. A carbon cost-gain model explains the observed patterns of xylem safety and efficiency. Plant Cell Environ. 34, 1819–1834 (2011).
Hari, P. & Kulmala, M. Station for measuring ecosystem-atmosphere relations (SMEARII). Boreal Environ. Res. 10, 315–322 (2005).
Lindow, S. E. The role of bacterial ice nucleation in frost injury to plants. Ann. Rev. Phytopathol. 21, 363–384 (1983).
Ashworth, E. N., Davis, G. A. & Anderson, J. A. Factors affecting ice nucleation in plant tissues. Plant Physiol. 79, 1033–1037 (1985).
Gross, D. C., Proebsting, E. L., Jr & Maccrindle-Zimmermann, H. Development, distribution and characteristics of intrinsic, nonbacterial ice nuclei in Prunus Wood. Plant Physiol. 88, 915–922 (1988).
Savage, V. M. et al. Hydraulic trade-offs and space filling enable better predictions of vascular structure and function in plants. P. Natl. Acad. Sci-Biol. 107, 22722–22727 (2010).
Wisniewski, M., Fuller, M., Glenn, D. M., Gusta, L., Duman, J. & Griffith, M. Extrinsic ince nucleation in plants: What are the factors involved and can they be manipulated in Plant Cold Hardiness: Gene Regulation and Genetic Engineering. (Eds. Li, P. H. & Palva, E. T.) 211–222 (Kluwer Academic, 2002).
Sperry, J. S. & Robson, D. J. Xylem cavitation and freezing in conifers in Conifer Cold Hardiness. (Eds. Bigras, F. J. & Colombo, S. J.) 121–136 (Kluwer, 2001).
Bilanski, W. K. & Tzeng, R. C. Supercooling as related to diameter of conducting vessels in plants. Transactions of the ASAE 23, 1334–1336 (1980).
Sevanto, S., Holbrook, N. M. & Ball, M. Freeze/thaw-induced embolism: probability of critical bubble formation depends on speed of ice formation. Front. Plant Sci. 3, 107 (2012).
Kulmala, M. et al. Toward direct measurement of atmospheric nucleation. Science 318, 89–92 (2007).
Heneghan, A. F. & Haymet, A. D. J. Liquid-to-crystal heterogeneous nucleation: Bubble accelerated nucleation of pure supercooled water. Chem. Phys. Lett. 368, 177–182 (2003).
Sperry, J. S. & Tyree, M. T. Mechanism of water stress-induced xylem embolism. Plant Physiol. 88, 581–587 (1988).
Choat, B., Jansen, S., Zwieniecki, M. A., Smets, E. & Holbrook, M. Changes in pit membrane porosity due to deflection and stretching: the role of vestured pits. J. Exp. Botany 55, 1569–1575 (2004).
Cochard, H., Hölttä, T., Herbette, S., Delzon, S. & Mencuccini, M. New insights into the mechanisms of water-stress-induced cavitation in conifers. Plant Physiol. 151, 949–954 (2009).
Villar-Salvador, P., Castro-Díez, P., Pérez-Rontomé, C. & Montserrat-Martí, G. Stem xylem features in three Quercus (Fagaceae) species along a climatic gradient in NE Spain. Trees 12, 90–96 (1997).
Meinzer, F. C., McCulloh, K. A., Lachenbruch, B., Woodruff, D. R. & Johnson, D. M. The blind men and the elephant: the impact of context and scale in evaluating conflicts between plant hydraulic safety and efficiency. Oecologia 164, 287–296 (2010).
Lintunen, A. & Kalliokoski, T. The effect of tree architecture on conduit diameter and frequency from small distal roots to branch tips in Betula pendula, Picea abies and Pinus sylvestris. Tree Physiol. 30, 1433–1447 (2010).
Chu, W. & So, W. S. Modeling the two stages of surfactant-aided soil washing. Water Research 35, 761–767 (2001).
Pruppacher, H. R. & Klett, J. D. Microphysics of Cloud and Precipitation (Reidel, 1997).
Turnbull, D. & Fisher, J. C. Rate of nucleation in condensed systems. J. Chem. Phys. 17, 71–72 (1949).
Winkler, P. M. et al. Heterogeneous nucleation experiments bridging the scale from molecular ion clusters to nanoparticles. Science 319, 1374–1377 (2008).
Hölttä, T., Vesala, T., Perämäki, M. & Nikinmaa, E. Relationships between embolism, stem water tension and diameter changes. J. Theor. Biol. 215, 23–38 (2002).
Wilson, P. W. & Haymet, A. D. J. The spread of nucleation temperatures of a sample of supercooled liquid is independent of the average nucleation temperature. J. Phys. Chem. B 116, 13472–13475 (2012).
Jarbeau, J. A., Ewers, F. W. & Davis, S. D. The mechanism of water-stress-induced embolism in two species of chaparral shrubs. Plant Cell Environ. 18, 189–196 (1995).
Acknowledgements
We thank Veli-Matti Kerminen, Eero Nikinmaa and Pertti Hari for discussions on the matter and Lauri Lindfors for technical assistance. The study was funded by the University of Helsinki three year's research grant, the Academy of Finland project number 1132561. The Academy of Finland Centre of Excellence (grant no. 1118615), the European Research Council Project (grant no. 227463-ATMNUCLE) and the Nordic Centre of Excellence CRAICC.
Author information
Authors and Affiliations
Contributions
A.L. performed the empirical part of the work and wrote the paper, T.H. and M.K. were responsible for the theoretical analysis and T.H. writing the theoretical analyses. All authors discussed the results and commented on the manuscript.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Electronic supplementary material
Supplementary Information
Supplementary Figures
Rights and permissions
This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivs 3.0 Unported License. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-nd/3.0/
About this article
Cite this article
Lintunen, A., Hölttä, T. & Kulmala, M. Anatomical regulation of ice nucleation and cavitation helps trees to survive freezing and drought stress. Sci Rep 3, 2031 (2013). https://doi.org/10.1038/srep02031
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep02031
This article is cited by
-
Differences in drought- and freeze-induced embolisms in deciduous ring-porous plant species in Japan
Planta (2016)
-
Irreversible diameter change of wood segments correlates with other methods for estimating frost tolerance of living cells in freeze-thaw experiment: a case study with seven urban tree species in Helsinki
Annals of Forest Science (2015)
-
Are the effects of winter temperatures on spring budburst mediated by the bud water status or related to a whole-shoot effect? Insights in the apple tree
Trees (2015)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.