Abstract
We perform extensive molecular dynamics simulations of the TIP4P/2005 model of water to investigate the origin of the Boson peak reported in experiments on supercooled water in nanoconfined pores and in hydration water around proteins. We find that the onset of the Boson peak in supercooled bulk water coincides with the crossover to a predominantly low-density-like liquid below the Widom line TW. The frequency and onset temperature of the Boson peak in our simulations of bulk water agree well with the results from experiments on nanoconfined water. Our results suggest that the Boson peak in water is not an exclusive effect of confinement. We further find that, similar to other glass-forming liquids, the vibrational modes corresponding to the Boson peak are spatially extended and are related to transverse phonons found in the parent crystal, here ice Ih.
Similar content being viewed by others
Introduction
One of the characteristic features of many glasses and amorphous materials is the onset1 of low-frequency collective modes (Boson peak) in the energy range 2 – 10 meV at low T, where the vibrational density of states (VDOS) g(ω) shows an excess over g(ω) ∝ ω2 predicted by the Debye model. Disordered materials are further known to exhibit many anomalous behaviors compared to their crystalline counterparts, such as the temperature dependence of thermal conductivity2,3 and specific heat4,5 at low temperatures. Many scenarios6,7 have been suggested to explain the physical mechanisms behind the Boson peak and related anomalies, but a comprehensive understanding has proved elusive.
Recent neutron scattering experiments on water confined in nanopores indicate the presence of a Boson peak8,9 around 5 – 6 meV (40 – 49 cm−1) emerging below 230 K in the incoherent dynamic structure factor. These results were tentatively interpreted as arising from a gradual change in the local structure of confined liquid water when crossing the Widom line temperature TW10. Earlier, neutron scattering has also been applied to protein hydration water11 and a Boson peak was found around 30 cm−1. TW corresponds to the loci of maxima of thermodynamic response functions in the one-phase region beyond the liquid-liquid critical point (LLCP) proposed to exist in supercooled liquid water12. A Widom line in the liquid-gas supercritical region in argon has recently been studied13,14 and found to be directly related to a dynamical crossover between liquid-like and gas-like properties, but the existence of a dynamical crossover in supercooled water is subject to some controversy15,16,17,18,19,20,21,22,23. Since the melting temperature is strongly depressed in nanoconfinement and in protein hydration water, deeply supercooled confined water has been used experimentally to infer the behavior of bulk water, which is more challenging to supercool. However, the similarity to bulk water has been called into question24,25 and it is thus important to further investigate the relationship between water in these different forms.
Both experimental9,26 and simulation27 studies suggest that the density relaxation of confined and hydration water at and slightly below the Widom temperature is of the order of a few tens of nanoseconds, implying that liquid water is still in metastable equilibrium over the experimental time scales involved28. The experimental observation of a Boson peak below TW in confined water thus suggests that the low-density-like liquid shares vibrational properties with the glassy state, as has been observed previously for other systems such as B2O329,30. On the other hand, the dynamic structure factor of crystalline ice exhibits a peak at a slightly higher frequency around 50 cm−1 31,32,33 as do the Raman spectra of ice Ih and proton-ordered ice XI34; in the latter case the peak becomes extremely sharp. These results indicate a connection between the dynamics of supercooled liquid and crystalline vibrational dynamics. Indeed, it has recently been suggested that Boson peaks observed in glasses are related to the vibrational dynamics of the parent crystal35.
To shed light on the question of whether bulk supercooled liquid water displays a Boson peak, we study the low-frequency dynamics of the TIP4P/2005 model of water which accurately reproduces a range of water properties36, including its anomalies37. This model has been found to exhibit a LLCP in the vicinity of PC = 1350 bar and TC = 193 K38. The associated Widom line has been shown to be accompanied by a structural crossover from a predominantly high-density liquid (HDL) structure to a predominantly low-density liquid (LDL) structure39,40 occurring at a temperature TW around 230 K at 1 bar. We find that this water model indeed displays a Boson peak in the bulk supercooled regime and that its onset coincides with the Widom temperature. Our analysis further shows that it derives from transverse acoustic modes in the parent crystal, ice Ih, in agreement with the recently proposed picture35. We further verify our results using another model of water, TIP5P and find also in this case an emergence of a Boson peak below the Widom line.
Results
Incoherent dynamic structure factors
A quantity that is readily accessible in inelastic neutron scattering experiments is the incoherent dynamic structure factor (DSF) SS(k,ω) which probes single-particle dynamics. To compare our simulation results with experiment we first calculate the self-intermediate scattering function

where  are the positions of oxygen atoms, N is the number of molecules and angular brackets denote an ensemble average and averaging over different
are the positions of oxygen atoms, N is the number of molecules and angular brackets denote an ensemble average and averaging over different  with the same modulus. In simulations the wave vector
with the same modulus. In simulations the wave vector  is defined as
is defined as  for integers (nx, ny, nz) and system size L. We perform the frequency decomposition of FS(k,t) to obtain the incoherent DSF
for integers (nx, ny, nz) and system size L. We perform the frequency decomposition of FS(k,t) to obtain the incoherent DSF

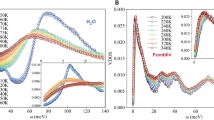
In Figs. 1(a) and 1(b), we show FS(k,t) and SS(k,ω) for supercooled liquid water simulations with N = 512 molecules at atmospheric pressure and different temperatures for k = 2 Å−1, i.e., the position of the first peak in the structure factor S(k). For T < TW, a minimum appears in FS(k,t) around 0.3 ps followed by oscillations up to around 10 ps. In the incoherent DSF these changes with temperature correspond to the emergence of sharp peaks at 20 and 25 cm−1 along with a broad peak centered around 37 cm−1. For comparison, we also show FS(k,t) and SS(k,ω) from hexagonal ice simulations at 100 K for two different system sizes. The connection between liquid and crystalline low-frequency dynamics will be further discussed below but we note here that the system size obviously affects the region ω < 40 cm−1.
(a) Fs(k,t) and (b) Ss(k,ω) for a range of temperatures 210–260 K at fixed k = 2.0 Å−1 and system size N = 512.SS(k,ω) at k = 2.0 Å−1 for ice at 100 K is also shown for two different system sizes, N = 432 and N = 3456. (c)–(d) show a comparison with Fs(k,t) and SS(k,ω) for a large N = 45,000 simulation at 210 K at k ≈ 1.6 Å−1. The broad peak around ω = 37 cm−1 is evidently independent of system size while the sharper peaks at lower frequency are not present in the large simulation.
Since low-frequency dynamics in supercooled liquids and glasses may be affected by finite-size effects41,42,43, we show in Figs. 1(c) and 1(d) a comparison with a much larger system, N = 45, 000 at 210 K. In FS(k,t) the oscillations are shifted to longer times while the minimum at 0.3 – 0.4 ps and subsequent peak around 0.9 ps are system-size independent. The sharp peaks in SS(k,ω) vanish in the large simulation but the broad peak around 37 cm−1 persists; we therefore label this peak of low-frequency excitations as the Boson peak. Comparing our simulation results with experimental neutron data on protein hydration water11 and on water in confinement8,9 reveals rather good agreement. Both the experimental energy position, 30 cm−1 for hydration water11 and 45 cm−1 for confined water8,9 and the temperature onset, T = 225 K8,9, are surprisingly well reproduced by the TIP4P/2005 model considering the approximate nature of classical force fields. Since we observe well-defined low-frequency modes in the incoherent DSF in the simulations of bulk water, we conclude that the Boson peak in supercooled water is not a consequence of confinement and that it would likely be detected also in experiments on bulk water, if sufficient supercooling could be achieved.
A connection to the Widom line in TIP4P/2005 is clearly present since a qualitative change of both FS(k,t) and SS(k,ω) takes place between 230 and 240 K. Our results thus imply that a Boson peak may also appear in other tetrahedral44 liquids, such as silicon and silica, for which simulations have indicated the existence of a liquid-liquid phase transition45,46. To confirm the connection between the Boson peak and the Widom line we have performed additional simulations of a different water potential, the TIP5P model47, which has been shown to exhibit a Widom line around 250 K27, 20 K above that for TIP4P/2005. As shown in the Supplementary Information, a Boson peak emerges also in this model and, indeed, it coincides with TW at 250 K.
Vibrational density of states
The Boson peak is commonly discussed in terms of the VDOS, g(ω). A distinct peak is often not seen in the VDOS itself but appears only in the reduced VDOS after normalizing by the squared frequency, g(ω)/ω2, which reveals the excess over the Debye model prediction g(ω) ∝ ω2. We calculate g(ω) as the Fourier transform of the oxygen velocity autocorrelation function, Cv(t):

where

The sum includes all N oxygen atoms in the system,  are the oxygen atom velocities and 〈…〉 denotes the ensemble average.
are the oxygen atom velocities and 〈…〉 denotes the ensemble average.
In Fig. 2(a) we show graphs of g(ω) for various temperatures. Below TW, g(ω) shows an onset of the same two sharp low-frequency peaks as observed in SS(k,ω) in Fig. 1. By simulating a range of different system sizes we can establish the system-size dependence of g(ω). The agreement for frequencies ω > 40 cm−1 is very good for different system sizes L, but the sharp low-frequency peaks shift to lower frequencies as the system size is increased. Indeed, both peaks extrapolate linearly to zero as 1/L, as seen in the inset of Fig. 2(a), suggesting that they disappear in the limit of infinite system size.
(a) VDOS of liquid water at supercooled temperatures and of hexagonal ice and (inset) inverse box-length dependence of the two lowest sharp peaks of the VDOS, extrapolating to zero frequency in the limit of infinite system size. In (a) the lowest-k transverse current spectrum is shown in the bottom part, illustrating that the sharp low-frequency peaks are low-k transverse modes. (b) Reduced vibrational density of states at low T calculated as [g(ω) − g(0)]/ω2 with an extrapolated g(0) to eliminate uncertainties related to the finite simulation time. Upon rapid cooling into a non-equilibrated LDA ice at 150 K and 100 K, the Boson peak is seen to shift to higher frequencies, approaching that of hexagonal ice. The inset in (b) shows the reduced VDOS calculated from the normal modes of inherent structures quenched from equilibrated T = 210 K configurations. The normal mode gNM(ω)/ω2 shows a Boson peak which is blue-shifted to about the same frequency as the crystal, suggesting that as the liquid structure is made harmonic the Boson peak frequency shifts to higher values saturating at about 50 cm−1.
As discussed in relation to Fig. 1, there is a low-frequency peak in SS(k,ω) for hexagonal ice at somewhat higher frequency compared to the supercooled liquid simulations, suggesting a link between the liquid and crystalline low-frequency modes. We investigate this by performing thermally non-equilibrated simulations at even lower temperatures where the TIP4P/2005 model vitrifies to a low-density amorphous (LDA)-like solid. The non-equilibrium simulations are performed by annealing the equilibrated metastable 210 K simulation with a cooling rate of 2·1010 K/s to reach target temperatures of 150 and 100 K. Figure 2(b) shows the reduced VDOS, [g(ω) – g(0)]/ω2 for simulations at 100, 150 and 210 K compared to the hexagonal ice simulation at 100 K. We subtract an extrapolated value of g(0) from g(ω) to eliminate uncertainties due to the finite length of the trajectories when evaluating the Fourier transform in Eq. (3). A clear shift to higher frequencies of the Boson peak is observed as the supercooled liquid simulations are cooled into the LDA glass region and the reduced VDOS at 100 K resembles the crystalline ice counterpart.
In the inset of Fig. 2(b), we show the reduced VDOS gNM(ω)/ω2 obtained from the normal modes of the liquid calculated from quenched configurations (i.e., energy minimized inherent structures) at T = 210 K. We find that the Boson peak in gNM(ω)/ω2 is blue-shifted to around 50 cm−1, close to the peak for hexagonal ice, compared to the velocity autocorrelation function VDOS which peaks at 37 cm−1. This suggests that a key difference in low-frequency vibrational properties between the LDL-like liquid below the Widom line and crystalline ice lies in the more anharmonic dynamics of the liquid phase.
Transverse and longitudinal correlation functions
Having established the existence of a Boson peak in supercooled water below the Widom line and its connection to low-frequency dynamics present in the parent crystal, ice Ih, we now turn to the study of transverse and longitudinal current correlations to clarify the nature of these low-frequency modes. We calculate longitudinal and transverse currents as


where  and
and  are unit vectors respectively parallel and perpendicular to k and ri(t) and vi(t) denote the oxygen atoms' position and velocity, respectively. The frequency decomposition of the longitudinal and transverse current autocorrelation functions is
are unit vectors respectively parallel and perpendicular to k and ri(t) and vi(t) denote the oxygen atoms' position and velocity, respectively. The frequency decomposition of the longitudinal and transverse current autocorrelation functions is

where α = L or T.
In the bottom part of Fig. 2(a) we show superimposed on the VDOS the transverse current correlation function (TCCF) CT(k,ω) at different temperatures for the lowest wave number k accessible in the N = 512 simulation boxes, i.e.,  = 2π(1, 0, 0)/L and permutations thereof. We see that the first sharp size-dependent low-frequency peak in the VDOS, which develops below TW, coincides exactly with the lowest-k TCCF and the second finite-size peak around 25 cm−1 coincides with the second-lowest-k TCCF (not shown). Returning to Fig. 1(d), the low-frequency side of the Boson peak is smoother in the large N = 45, 000 simulations and the sharp peaks related to the lowest-k transverse currents are instead seen at frequencies below 10 cm−1. We thus conclude that the sharp system size dependent low-frequency peaks around the Boson peak frequency and below are predominantly transverse excitations, consistent with previous findings for amorphous silica43.
= 2π(1, 0, 0)/L and permutations thereof. We see that the first sharp size-dependent low-frequency peak in the VDOS, which develops below TW, coincides exactly with the lowest-k TCCF and the second finite-size peak around 25 cm−1 coincides with the second-lowest-k TCCF (not shown). Returning to Fig. 1(d), the low-frequency side of the Boson peak is smoother in the large N = 45, 000 simulations and the sharp peaks related to the lowest-k transverse currents are instead seen at frequencies below 10 cm−1. We thus conclude that the sharp system size dependent low-frequency peaks around the Boson peak frequency and below are predominantly transverse excitations, consistent with previous findings for amorphous silica43.
The dispersion relations for transverse and longitudinal current spectra, CT(k,ω) and CL(k,ω) at T = 210 K, are shown in Fig. 3 (the current spectra are shown in the Supplementary Material). We obtain dispersion relations by fitting damped harmonic oscillator (DHO)48 lines to both longitudinal and transverse spectra.
Longitudinal (filled circles) and transverse (filled squares) dispersion relations calculated from the peak positions of ωL(k) in CL(k,ω) and ωT(k) in CT(k,ω) for N = 2048 and T = 210 K. For k < 0.5 Å−1, longitudinal spectra exhibit one dispersive branch (LA: black filled circles), while for k > 0.5 Å−1, the longitudinal spectra exhibit three excitations –low and high frequency weakly dispersive excitations (shown in orange and red filled circles).For k < 0.5 Å−1, transverse current spectra exhibit only one dispersive excitation (TA: blue filled squares) while for k > 0.5 Å−1, it exhibits both the dispersive branch as well as a weakly dispersive excitation (green filled squares) at ω ≈ 260 cm−1. For information on extraction of the dispersion relation see Fig. S2.
At small k below 0.5 Å−1, the longitudinal current spectrum, CL(k,ω), shows only one acoustic dispersing excitation. For k > 0.5 Å−1, CL(k,ω) shows the existence of three excitations and can be fit with three DHO lines. Besides the dispersing excitation at intermediate frequency, two other weakly dispersing excitations appear—one at low frequency around 50 cm−1 and the other at high frequency around 260 cm−1. The intensity of these excitations in CL(k,ω) increases upon further increase of k. Transverse current spectra CT(k,ω) exhibit an acoustic dispersing excitation for k < 0.5 Å−1. For k > 0.5 Å−1, CT(k,ω) develops a peak at ω ≈ 260 cm−1, the same excitation as in the longitudinal current spectra. Transverse and longitudinal modes are thus strongly mixed above 0.5 Å−1 as has been found previously also for the SPC/E water model49. Moreover, the mixing happens at both high frequencies (ω ≈ 260 cm−1) and low frequencies (ω < 60 cm−1) as evident from transverse excitations appearing in longitudinal spectra. We note that the band at 260 cm−1 in liquid water is associated with four-coordinated water molecules since low-frequency Raman spectra of water down to –20°C showed its intensity to increase with decreasing temperature50 and hexagonal ice also displays a strong band near this frequency51. Hence, the emergence of the 260 cm−1 band in both CL(k,ω) and CT(k,ω) suggests that liquid water at this temperature exhibits networks of four-coordinated molecules over length scales as large as 2π/0.5 Å−1 ~ 13 Å. This observation is also consistent with recent studies where it is shown that the sizes of clusters of highly tetrahedral molecules increases below the Widom temperature3,44.
The emergence of an additional, high-frequency excitation in CL(k,ω) and CT(k,ω) around 260 cm−1 for k > 0.5 Å−1 suggests a low-frequency liquid-like and a high-frequency solid-like behavior of the longitudinal and transverse spectra at this length scale and a concomitant pile-up of spectral intensity takes place in the Boson peak regime.
To get further insights into the longitudinal or transverse character of the Boson peak, we compare cumulatively integrated spectra over k for different frequencies for both the transverse and longitudinal parts,  and
and  , defined as
, defined as

where α = L or T and kmin = 2π/L is the smallest wave number accessible in our system of box size L.  thus describes the total contribution of longitudinal and transverse modes with different wave numbers up to k for a given frequency ω. In Fig. 4(a)–(b) we show normal and cumulatively integrated current spectra for several frequencies ωB in the Boson peak region around 37 cm−1. It can be clearly seen that transverse modes are dominant in the Boson peak frequency regime for k > 0.5 Å−1.
thus describes the total contribution of longitudinal and transverse modes with different wave numbers up to k for a given frequency ω. In Fig. 4(a)–(b) we show normal and cumulatively integrated current spectra for several frequencies ωB in the Boson peak region around 37 cm−1. It can be clearly seen that transverse modes are dominant in the Boson peak frequency regime for k > 0.5 Å−1.
Localization analysis
A number of studies on amorphous materials have found that the modes in the Boson peak frequency range are localized or quasi-localized52,53. In order to investigate whether this holds also for TIP4P/2005 water below the Widom line TW, we calculate the degree of localization by performing a normal mode analysis of quenched (or inherent) structures, obtained by energy-minimizing snapshots from simulation trajectories. A measure of the degree of localization of a vibrational mode is the frequency-dependent participation ratio54,55 pμ for mode μ

where  is the contribution of all degrees of freedom of molecule i to the normal mode μ. The participation ratio is unity when all molecules contribute equally to the normal mode in consideration, while p = 1/N if only one molecule contributes to the total energy of the mode. Hence, for an extended mode pμ is close to unity and does not depend on the system size while for a localized mode it is small and scales with system size as 1/N. One way to determine the extent of localization is thus to inspect the system-size dependence of the participation ratio. We find (see Fig. 5(a)) that the participation ratio is quite large, around 0.6, for the modes with frequency below 50 cm−1, the region of the Boson peak. Apart from the sharp finite-size peaks, the participation ratio for the modes in the region of the Boson peak show only a weak system size dependence, suggesting that the modes giving rise to the Boson peak are not localized but extended.
is the contribution of all degrees of freedom of molecule i to the normal mode μ. The participation ratio is unity when all molecules contribute equally to the normal mode in consideration, while p = 1/N if only one molecule contributes to the total energy of the mode. Hence, for an extended mode pμ is close to unity and does not depend on the system size while for a localized mode it is small and scales with system size as 1/N. One way to determine the extent of localization is thus to inspect the system-size dependence of the participation ratio. We find (see Fig. 5(a)) that the participation ratio is quite large, around 0.6, for the modes with frequency below 50 cm−1, the region of the Boson peak. Apart from the sharp finite-size peaks, the participation ratio for the modes in the region of the Boson peak show only a weak system size dependence, suggesting that the modes giving rise to the Boson peak are not localized but extended.
(a) Frequency dependent participation ratio for two system sizes, N = 512 and N = 1024.(b) Spatial dependence of the amplitude of normal modes Amax(r) in the Boson peak regime. For a comparison, Amax(r) for ω = 400 ± 5 cm−1 where the modes are localized is also shown. The value of Amax(0) is normalized to 1 for the range of frequencies shown.
We next introduce a function Amax(r) defined as the maximum displacement of molecules at a distance r from the molecule with the largest displacement in the normal mode. For a localized mode a rapid decay of Amax(r) should be seen. In Fig. 5(b) we show average Amax(r) for the normal modes in two different frequency regimes – for the Boson peak regime (ωB = 45 ± 2.5 cm−1, note that the frequency of the Boson peak for the quenched configuration is shifted to higher frequency compared to the Boson peak frequency ωB ≈ 37 cm−1 of the liquid at T = 210 K, see inset of fig. 2(b)) and in comparison we also show average Amax(r) for modes in the range of ω = 400 ± 5 cm−1, which is a range of localized vibrations. While for ω = 400 ± 5 cm−1, Amax(r) decays rapidly to zero, for the Boson peak region it does not, suggesting again an extended nature of the Boson peak modes.
Discussion
The low-frequency vibrations of a classical potential model of water, TIP4P/2005, are investigated in the supercooled temperature regime to clarify the origin of the Boson peak reported from inelastic neutron scattering experiments below around 225 K in nano-confined8,9 and protein-hydration water11. We find that sharp low-frequency peaks emerge in the incoherent dynamic structure factor and the reduced density of states of the simulated liquid water as the system is cooled below the Widom line, but a system-size investigation reveals that in the limit of an infinitely large simulation box these peaks extrapolate to zero frequency. The sharp finite-size peaks are seen to coincide exactly with the low wave-number acoustic branch of the transverse current correlation functions, reflecting a strong contribution of transverse modes in this frequency region. However, we find a broad Boson peak centered around 37 cm−1 which is unaffected by system size and for which the frequency region and temperature of onset in the incoherent DSF agree well with neutron experiments on confined water. Due to its lower melting temperature, water in confinement has been used experimentally to infer the behavior of bulk water below the bulk homogeneous nucleation temperature. The validity of this comparison has been questioned, but the good agreement observed here in the low-frequency vibrational dynamics lends support to the view of confinement as useful in the study of supercooled bulk water, at least for low-frequency vibrational properties.
The frequency of the Boson peak in supercooled TIP4P/2005 water as observed in the reduced VDOS changes as the simulation is annealed into the LDA glass region and approaches ω = 45 cm−1. This is also the frequency at which hexagonal ice simulations display a peak in vibrational spectra deriving from the transverse acoustic branch, as has been observed experimentally31,32,33. Thus, upon lowering the temperature below the Widom line, the low-frequency dynamics of the system progressively changes from LDL-like to LDA glass and to the dynamics found in hexagonal ice. A similar shift to higher frequencies is observed in normal-mode spectra of inherent structures quenched from liquid at temperatures below the Widom line, indicating that the lower frequency of the Boson peak in the liquid below the Widom line, compared to the transverse acoustic peak in the ice, is a result of the more anharmonic nature of the vibrational modes in the liquid.
Recent work by Chumakov et al.35 on glasses suggests that there is no excess in the actual number of states at the Boson peak and hence no additional modes compared to the crystal. The Boson peak is thus related to the transverse acoustic singularity of the underlying crystal structure. Transverse modes have also been firmly connected to the Boson peak in other works43,56. Indeed, our studies of transverse and longitudinal correlation functions suggest that low-frequency transverse phonons contribute the most to the Boson peak intensity in the range of wave numbers where both the longitudinal and transverse phonons show a solid-like response over large length scales, namely emergence of a high-frequency peak in both longitudinal and transverse spectra at ω ≈ 260 cm−1 for k > 0.5 Å−1. The appearance of this high-frequency excitation associated with four-coordinated molecules in longitudinal and transverse spectra coincides with a pile up of intensities in the Boson peak regime.
To conclude, our results indicate that liquid water displays a Boson peak below the Widom line temperature TW. Both the onset temperature and energy position are similar to what has been observed experimentally for confined water8,9. We find that as the liquid crosses over to a low-density-like liquid structure below TW the low-frequency dynamics of the liquid changes to resemble that of the underlying crystal, ice Ih. The Boson peak in supercooled water is thus a manifestation of the transverse acoustic singularity of the crystal and may therefore be a general phenomenon in tetrahedral liquids showing a liquid-liquid phase transition.
Methods
We simulate TIP4P/200536 water for a range of temperatures at atmospheric pressure. Equilibration is first performed in the NPT ensemble, using the Nosé-Hoover thermostat and Parrinello-Rahman barostat to attain constant temperature and pressure. The equilibrated densities are then used in equilibration NVT runs performed over multiple structural relaxation times, after which we switch to the NVE ensemble to compute the relevant dynamical quantities. The equations of motion are integrated with a time step of 0.2–1.0 fs, depending on the observed energy conservation. Most simulations are performed using N = 512 molecules, but to quantify the finite-size effects we simulate larger systems up to N = 45,000. Simulation temperatures between 210 and 260 K at P = 1 atm were chosen so that the system crosses TW, the temperature where maxima in response functions are observed. To confirm the connection between the Widom line TW and the onset temperature of the Boson peak we repeat the above simulation protocol for the TIP5P water model47 at temperatures between 240 and 270 K (see Supplementary Information).
We perform non-equilibrium simulations of TIP4P/2005 at 100 and 150 K by rapidly cooling from 210 K with a cooling rate of 2·1010 K/s and then switching to the NVE ensemble to calculate dynamical properties.
For the calculation of the participation ratio and the function Amax(r), equilibrium configurations at a given temperature were quenched to obtain the configurations corresponding to the nearest local minimum of the system. Then we calculate eigenmodes and eigenvalues corresponding to vibrational modes about this local energy minimum by diagonalizing the Hessian matrix with respect to the generalized coordinates. We use the flexible version of the model and hence all degrees of freedom to calculate the Hessian (see Refs. 54,55,57 for a more detailed explanation of the formalism and method).
References
Angell, C. A. Boson peaks and floppy modes: some relations between constraint and excitation phenomenology and interpretation, of glasses and the glass transition. J. Phys.: Condens. Matter 16, S5153–S5164 (2004).
Cahill, D. G. & Pohl, R. O. Thermal conductivity of amorphous solids above the plateau. Phys. Rev. B 35, 4067–4073 (1987).
Kumar, P. & Stanley, H. E. Thermal conductivity minimum: A new water anomaly. J. Phys. Chem. B 115, 14269–14273 (2011).
Berman, R. Thermal conductivity of glasses at low temperatures. Phys. Rev. 76, 315–316 (1949).
Zeller, R. C. & Pohl, R. O. Thermal conductivity and specific heat of noncrystalline solids. Phys. Rev. B 4, 2029–2041 (1971).
Nakayama, T. Boson peak and terahertz frequency dynamics of vitreous silica. Rep. Prog. Phys. 65, 1195–1242 (2002).
Angell, C. A., Ngai, K. L., McKenna, G. B., McMillan, P. F. & Martin, S. W. Relaxation in glassforming liquids and amorphous solids. J. Appl. Phys. 88, 3113–3147 (2000).
Chen, S.-H. et al. Dynamic crossover phenomenon in confined supercooled water and its relation to the existence of a liquid-liquid critical point in water. In: AIP Conference Proceedings volume 982, 39–52 (2008).
Chen, S.-H. et al. Evidence of dynamic crossover phenomena in water and other glassforming liquids: experiments, MD simulations and theory. J. Phys.: Condens. Matter 21, 504102 (2009).
Kumar, P. et al. Glass transition in biomolecules and the liquid-liquid critical point of water. Phys. Rev. Lett. 97, 177802 (2006).
Paciaroni, A., Bizzarri, A. R. & Cannistaro, S. Neutron scattering evidence of a boson peak in protein hydration water. Phys. Rev. E 60, 2476–2479 (1999).
Poole, P. H., Sciortino, F., Essmann, U. & Stanley, H. E. Phase behaviour of metastable water. Nature 360, 324–328 (1992).
Simeoni, G. et al. The Widom line as the crossover between liquid-like and gas-like behaviour in supercritical fluids. Nature Physics 6, 503–507 (2010).
Gorelli, F. A. et al. Dynamics and thermodynamics beyond the critical point. Sci. Rep. 3, 1203 (2013).
Faraone, A., Liu, L., Mou, C.-Y., Yen, C.-W. & Chen, S.-H. Fragile-to-strong liquid transition in deeply supercooled confined water. J. Chem. Phys. 121, 10843 (2004).
Mamontov, E. Observation of fragile-to-strong liquid transition in surface water in CeO2 . J. Chem. Phys. 123, 171101 (2005).
Swenson, J., Jansson, H. & Bergman, R. Relaxation processes in supercooled confined water and implications for protein dynamics. Phys. Rev. Lett. 96, 247802 (2006).
Mallamace, F. et al. The fragile-to-strong dynamic crossover transition in confined water: nuclear magnetic resonance results. J. Chem. Phys. 124, 161102 (2006).
Swenson, J., Jansson, H., Hedström, J. & Bergman, R. Properties of hydration water and its role in protein dynamics. J. Phys.: Condens. Matter 19, 205109 (2007).
Khodadadi, S. et al. The origin of the dynamic transition in proteins. J. Chem. Phys. 128, 195106 (2008).
Pawlus, S., Khodadadi, S. & Sokolov, A. P. Conductivity in hydrated proteins: no signs of the fragile-to-strong crossover. Phys. Rev. Lett. 100, 108103 (2008).
Vogel, M. Origins of apparent fragile-to-strong transitions of protein hydration waters. Phys. Rev. Lett. 101, 225701 (2008).
Vogel, M. Temperature-dependent mechanisms for the dynamics of protein-hydration waters: a molecular dynamics simulation study. J. Phys. Chem. B 113, 9386–9392 (2009).
Ricci, M. A., Bruni, F., Gallo, P., Rovere, M. & Soper, A. K. Water in confined geometries: experiments and simulations. J. Phys.: Condens. Matter 12, A345 (2000).
Mattea, C., Qvist, J. & Halle, B. Dynamics at the protein-water interface from 17O spin relaxation in deeply supercooled solutions. Biophys. J. 95, 2951–2963 (2008).
Chen, S.-H. et al. Observation of fragile-to-strong dynamic crossover in protein hydration water. Proc. Nat. Acad. Sci. USA 103, 9012–9016 (2006).
Xu, L. et al. Relation between the Widom line and the dynamic crossover in systems with a liquid–liquid phase transition. Proc. Natl. Acad. Sci. USA 102, 16558–16562 (2005).
Liu, L., Chen, S.-H., Faraone, A., Yen, C.-W. & Mou, C.-Y. Pressure dependence of fragile-to-strong transition and a possible second critical point in supercooled confined water. Phys. Rev. Lett. 95, 117802 (2005).
Börjesson, L., Hassan, A. K., Swenson, J., Torell, L. M. & Fontana, A. Is there a correlation between the first sharp diffraction peak and the low frequency vibrational behavior of glasses? Phys. Rev. Lett. 70, 1275–1278 (1993).
Sokolov, A. P., Kisliuk, A., Quitmann, D., Kudlik, A. & Rössler, E. The dynamics of strong and fragile glass formers: vibrational and relaxation contributions. J. Non-Cryst. Solids 172, 138–153 (1994).
Bermejo, F. J., Alvarez, M., Bennington, S. M. & Vallauri, R. Absence of anomalous dispersion features in the inelastic neutron scattering spectra of water at both sides of the melting transition. Phys. Rev. E 51, 2250 (1995).
Yamamuro, O. et al. Low-energy excitations of vapor-deposited amorphous ice and its annealing and methanol-doping effects studied by inelastic neutron scattering. J. Chem. Phys. 115, 9808 (2001).
Yamamuro, O., Matsuo, T., Tsukushi, I. & Onoda-Yamamuro, N. Inelastic neutron scattering and low-energy excitation of amorphous SF6 hydrate prepared by vapor-deposition technique. Can. J. Phys. 81, 107–114 (2003).
Abbe, K. & Shigenari, T. Raman spectra of proton ordered phase XI of ice I. Translational vibrations below 350 cm−1. J. Chem. Phys. 134, 10506 (2011).
Chumakov, A. I. et al. Equivalence of the Boson peak in glasses to the transverse acoustic van Hove singularity in crystals. Phys. Rev. Lett. 106, 225501 (2011).
Abascal, J. L. F. & Vega, C. A general purpose model for the condensed phases of water: TIP4P/2005. J. Chem. Phys. 123, 234505 (2005).
Pi, H. L. et al. Anomalies in water as obtained from computer simulations of the TIP4P/2005 model: density maxima and density, isothermal compressibility and heat capacity minima. Mol. Phys. 107, 365–374 (2009).
Abascal, J. L. F. & Vega, C. Widom line and the liquid–liquid critical point for the TIP4P/2005 water model. J. Chem. Phys. 133, 234502 (2010).
Wikfeldt, K. T., Huang, C., Nilsson, A. & Pettersson, L. G. M. Enhanced small-angle scattering connected to the Widom line in simulations of supercooled water. J. Chem. Phys. 134, 214506 (2011).
Wikfeldt, K. T., Nilsson, A. & Pettersson, L. G. M. Spatially inhomogeneous bimodal inherent structure in simulated liquid water. Phys. Chem. Chem. Phys. 13, 19918–19924 (2011).
Horbach, J., Kob, W., Binder, K. & Angell, C. A. Finite size effects in simulations of glass dynamics. Phys. Rev. E 54, 5897–5900 (1996).
Kim, K. & Yamamoto, R. Apparent finite-size effects in the dynamics of supercooled liquids. Phys. Rev. E 61, 41–44 (2000).
Horbach, J., Kob, W. & Binder, K. High frequency sound and the boson peak in amorphous silica. Eur Phys J B 19, 531–543 (2001).
Errington, J. R. & Debenedetti, P. G. Relationship between structural order and the anomalies of liquid water. Nature 409, 318–321 (2001).
Sastry, S. & Angell, C. A. Liquid–liquid phase transition in supercooled silicon. Nature Mater. 2, 739–743 (2003).
Saika-Voivoid, I., Sciortino, F. & Poole, P. H. Computer simultions of liquid silica: Equation of state and liquid-liquid phase transition. Phys. Rev. E 63, 011202 (2000).
Mahoney, M. W. & Jorgensen, W. L. A five-site model for liquid water and the reproduction of the density anomaly by rigid, nonpolarizable potential functions. J. Chem. Phys. 112, 8910–8922 (2000).
Ruocco, G. & Sette, F. The history of the ”fast sound” in liquid water. Condens. Matter Phys. 11, 29–46 (2008).
Sampoli, M., Ruocco, G. & Sette, F. Mixing of longitudinal and transverse dynamics in liquid water. Phys. Rev. Lett. 79, 1678–1681 (1997).
Krishnamurthy, S. Bansil, R. & Wiafe-Akinten, J. Low-frequency Raman spectrum of supercooled water. J. Chem. Phys. 79, 5863–5870 (1983).
Klug, D. D., Whalley, E., Svensson, E. C., Root, J. H. & Sears, V. F. Densities of vibrational states and heat capacities of crystalline and amorphous H2O ice determined by neutron scattering. Phys. Rev. B 44, 841–844 (1991).
McIntosh, C., Toulouse, J. & Tick, P. The Boson peak in alkali silicate glasses. J. Non-Cryst. Solids 222, 335–341 (1997).
Novikov, V. N., Duval, E., Kisliuk, A. & Sokolov, A. P. A model of low frequency Raman scattering in glasses: Comparison of Brillouin and Raman data. J. Chem. Phys. 102, 4691–4698 (1995).
Bell, R. J., Dean, P. & Hibbins-Butler, D. C. The vibrational spectra of vitreous silica, germania and beryllium fluoride. J. Phys. C: Solid State Phys. 3, 2111–2118 (1970).
Sastry, S., Stanley, H. E. & Sciortino, F. Low frequency depolarized Raman spectra in water: Results from normal mode analysis. J. Chem. Phys. 100, 5361–5366 (1994).
Shintani, H. & Tanaka, H. Universal link between the boson peak and transverse phonons in glass. Nature Mater. 7, 870–877 (2008).
Matharoo, G. S., Shajahan, M., Razul, G. & Poole, P. H. Spectral statistics of the quenched normal modes of a network-forming molecular liquid. J. Chem. Phys. 130, 124512 (2009).
Acknowledgements
We thank S. V. Buldyrev and S. Sastry for helpful discussions. The simulations were in part performed using resources provided by the Swedish National Infrastructure for Computing (SNIC) at the NSC and HPC2N centers. LGMP, KTW and DS were supported by the Swedish Research Council. KTW is also supported by the Icelandic Research Fund through the START programme. PK acknowledges the support of National Academies Keck Future Initiatives award. HES thanks NSF Grants No. CHE0911389, No. CHE0908218 and No. CHE-1213217.
Author information
Authors and Affiliations
Contributions
P.K. and K.T.W. contributed equally. P.K., K.T.W. and D.S. performed simulations. P.K., K.T.W., D.S., L.P. and H.E.S. contributed to the analysis and writing of the paper.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Electronic supplementary material
Supplementary Information
Supplementary Information Main Text
Supplementary Information
Normal modes corresponding to low frequency peak 1
Supplementary Information
Normal modes corresponding to low frequency peak 2
Supplementary Information
Normal modes corresponding to Boson Peak
Rights and permissions
This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivs 3.0 Unported License. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-nd/3.0/
About this article
Cite this article
Kumar, P., Wikfeldt, K., Schlesinger, D. et al. The Boson peak in supercooled water. Sci Rep 3, 1980 (2013). https://doi.org/10.1038/srep01980
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep01980
This article is cited by
-
The ω3 scaling of the vibrational density of states in quasi-2D nanoconfined solids
Nature Communications (2022)
-
Experimental tests for a liquid-liquid critical point in water
Science China Physics, Mechanics & Astronomy (2020)
-
The Boson peak interpretation and evolution in confined amorphous water
Science China Physics, Mechanics & Astronomy (2019)
-
The hydrogen-bond collective dynamics in liquid methanol
Scientific Reports (2016)
-
Combinatorial Broadening Mechanism of O–H Stretching Bands in H-Bonded Molecular Clusters
Journal of Applied Spectroscopy (2016)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.

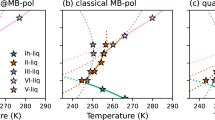




 and
and  as function of k (see Eq. 8). Several frequencies ωB in the Boson peak frequency regime are shown.
as function of k (see Eq. 8). Several frequencies ωB in the Boson peak frequency regime are shown.