Abstract
State distillation is the process of taking a number of imperfect copies of a particular quantum state and producing fewer better copies. Until recently, the lowest overhead method of distilling states  produced a single improved |A〉 state given 15 input copies. New block code state distillation methods can produce k improved |A〉 states given 3k + 8 input copies, potentially significantly reducing the overhead associated with state distillation. We construct an explicit surface code implementation of block code state distillation and quantitatively compare the overhead of this approach to the old. We find that, using the best available techniques, for parameters of practical interest, block code state distillation does not always lead to lower overhead, and, when it does, the overhead reduction is typically less than a factor of three.
produced a single improved |A〉 state given 15 input copies. New block code state distillation methods can produce k improved |A〉 states given 3k + 8 input copies, potentially significantly reducing the overhead associated with state distillation. We construct an explicit surface code implementation of block code state distillation and quantitatively compare the overhead of this approach to the old. We find that, using the best available techniques, for parameters of practical interest, block code state distillation does not always lead to lower overhead, and, when it does, the overhead reduction is typically less than a factor of three.
Similar content being viewed by others
Introduction
One of the grand challenges of 21st-century physics and engineering is to construct a practical large-scale quantum computer. One of the primary ways theoretical research can reduce the magnitude of this challenge is to devise ways of performing a given quantum computation using fewer qubits and quantum gates while simultaneously leaving all other engineering targets unchanged.
State distillation1,2 is a procedure required by the majority of concatenated quantum error correction (QEC) schemes3,4,5,6,7, with the exception of the Steane code8 and required by the majority of topological QEC schemes9,10,11,12,13,14,15,16,17,18,19, with the exception of a 3-D color code20 and a non-Abelian code21. As such, the search for lower overhead methods of implementing state distillation is of great importance.
Two recent works22,23 are of particular note, both independently proposing block code based methods taking 3k + 8 imperfect copies of a particular state and distilling k improved copies. These works built on the approach of24. However, in all cases, a detailed analysis of the overhead in terms of qubits and quantum gates was not performed. In this work, we explicitly construct a surface code19 implementation of one of these block code state distillation methods23. Given a quantum computer consisting of a 2-D array of qubits with nearest neighbor interactions25,26,27,28, there is compelling evidence that the surface code is the lowest overhead code achievable29. Furthermore, this code can be used to achieve time-optimal quantum computation30. The surface code therefore provides an excellent framework to gauge the cost of the new block code state distillation methods.
The discussion shall be organized as follows. We first illustrate a quantum circuit that can be used to perform block code state distillation. Next we perform a detailed comparison of the overhead of concatenated 15-to-1 and block code state distillation. We then summarize our results and discuss further work.
Results
Block code state distillation
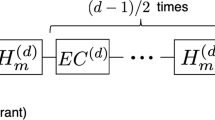
Figure 1 illustrates a quantum circuit to implement the block code state distillation protocol of Jones23. This protocol uses a delayed application of T gates to eliminate X errors as illustrated in Figure 2. Details of the state distillation protocol can be found in the methods section.
Extendable quantum circuit for block code state distillation.
This circuit takes 3k + 8 copies of |A〉, each with probability p of error and producing k copies, each with approximate probability (3k + 1)p2 of error. In the figure, k = 4. The repeating unit cell is highlighted. Note that k must be even. A box encircles output numbers. Each T gate consumes one |A〉 state as shown in Figure 2.
In Figure 3 we show a rearranged version of Figure 1 that is more convenient for physical implementation. A surface code CNOT is shown in Figure 412,13,19. This topological structure can be arbitrarily deformed without changing the computation it implements. This permits direct implementation of the bent CNOTs (Figure 5). This can be compressed to Figure 6. See the supplementary material for a step-by-step description of the compression process and larger versions of these figures.
Constant depth extendable circuit implementing block code state distillation.
This example takes (3k + 8)-to-k state distillation for k = 4. Boxes encircle output numbers. Using the surface code, bent CNOTs can be implemented exactly as shown (see Figure 5). The repeating unit cell is highlighted.
CNOT circuits in the surface code.
(a) CNOT quantum circuit example. (b) Equivalent surface code CNOT12,13,19. Time runs from left to right. The scale of the figure is set by the code distance d. Small cubes are d/4 a side. Longer blocks have length d. Each unit of d in the temporal direction represents a round of error detection. Each unit of d in the two spatial directions represents two qubits. The structures are called defects and represent space-time regions in which error detection has been turned off.
Depth 31 canonical surface code implementation of block code state distillation.
This structure is a direct mapping of Figure 3. A larger version of this figure can be found in the supplementary material.
Depth 12 compressed surface code implementation block code state distillation.
A compressed version of of Figure 3. A larger version of this figure can be found in the supplementary material, along with step-by-step images explaining how it was obtained.
Overhead comparison
Suppose we desire logical |A〉 states with error pout and can prepare logical |A〉 states with error pin. We will consider values pin = 10−2, 10−3 and 10−4, as this covers the plausibly achievable range given the current state of quantum technology and values pout = 10−5, …, 10−20, as this covers essentially the entire range that could forseeably be useful in a practical quantum algorithm.
The process of preparing arbitrary logical states is called state injection and in the surface code approximately 10 gates are required to work before error protection is available19. It is therefore reasonable to assume the physical gate error rate pg is an order of magnitude less than pin. The logical error rate per round of error detection in a square patch of surface code as a function of pg and code distance d is shown in Figure 731.
Focusing initially on the simpler 15-to-1 concatenated distillation process, the topological structure required for a single level of distillation is shown in Figure 8. Dark structures are called dual defects, light structures are called primal defects. The geometric volume of the structure can be defined as the number of primal cubes in a minimum volume cuboid containing the structure. In this case, the structure is 6 cubes high, 16 cubes wide and 2 cubes deep, for a total V = 192. Each primal cube has dimensions d/4, each longer prism has length d. Each unit of d in the temporal direction (up in Figure 8) corresponds to a round of surface code error detection, each unit of d in the two spatial directions corresponds to two qubits. It is therefore straightforward to convert the geometric volume to an absolute volume in units of qubits-rounds. A fragment of the complete structure of edge length 5d/4 with a primal cube potentially centered within it is called a plumbing piece. Geometric volume is therefore in units of plumbing pieces. In order to calculate the overhead of state distillation, we will need to first reasonably upper bound the probability of logical error per plumbing piece.
Standard 15-1 state distillation in the surface code.
State distillation method taking 15 input |A〉 states, each with error p and producing with probability 1 − 15p a single output |A〉 state with error 35p3 1,29. Each unit of d in the temporal direction (up in this figure) corresponds to a round of surface code error detection, each unit of d in the two spatial directions corresponds to two qubits.
Consider a forest of straight, d separated parallel defects of circumference d, as shown in Figure 9. Each defect can be assumed responsible for logical errors connecting it to two of its neighboring defects and also self encircling logical errors. The probability of each of these types of logical error per round of error detection can be upper bounded by the probability of logical error per round of error detection of a square surface. There are more potential logical errors per round connecting opposing boundaries in a square surface of distance d than there are connecting distinct defects or encircling a single defect.
Defect arrangement for the surface code.
A forest of d separated straight defects of circumference d. Two square surfaces of dimension d × d have been included. The logical error rate of these surfaces upper bounds the probability of a logical error connecting neighboring defects and encircling a single defect. Time runs vertically. In the temporal direction, each unit of d represents a round of error detection. In the spatial directions, each unit of d represents two qubits.
Given the per round probability of logical error pL(d, pg) of a square surface, we can upper bound the logical error rate of a plumbing piece PL(d,pg) by 2 × 3 × 5d/4 × pL(d,pg), where the factor of 5d/4 is for the number of rounds of error detection in a plumbing piece, the factor of 3 is for the number of distinct classes of logical error and the factor of 2 is due to the fact that a single plumbing piece can contain both a primal and a dual defect. From Figure 7, pL(d,pg) ~ 0.1(100pg)(d+1)/2, implying PL(d,pg) ~ d(100pg)(d+1)/2.
Given input error rate pin, with 15-to-1 state distillation the output error rate can be made arbitrarily close to pdist = 35p3 by using a sufficiently large d to eliminate logical errors during distillation. However, logical errors do not need to be completely eliminated and we define  to be the amount of logical error introduced. For
to be the amount of logical error introduced. For  , the logical circuitry introduces as much error as distillation fails to eliminate and
, the logical circuitry introduces as much error as distillation fails to eliminate and  . We shall assume that logical failure anywhere during distillation leads to the output being incorrect and accepted.
. We shall assume that logical failure anywhere during distillation leads to the output being incorrect and accepted.
Let us consider a specific example. Suppose pin = 10−3, our desired pout = 10−15 and our chosen  . Our top level of state distillation must therefore have a probability of logical error no more than
. Our top level of state distillation must therefore have a probability of logical error no more than  . Given V = 192 for 15-to-1 state distillation, this means we need VPL(d,pg) = 192PL(d,10−4) < 5 × 10−16, implying d = 19. The states input to the top level of distillation must have an error rate no more than
. Given V = 192 for 15-to-1 state distillation, this means we need VPL(d,pg) = 192PL(d,10−4) < 5 × 10−16, implying d = 19. The states input to the top level of distillation must have an error rate no more than  . Since this is less than pin, more state distillation is required. Our second level of state distillation must have a probability of logical error no more than
. Since this is less than pin, more state distillation is required. Our second level of state distillation must have a probability of logical error no more than  , implying d = 9. The states input to the second level of distillation must have an error rate no more than
, implying d = 9. The states input to the second level of distillation must have an error rate no more than  . Since this is greater than pin, no further distillation is required. The absolute volume of the d = 19 top level and 15 d = 9 second level distillation structures is 3.1 × 107 qubits-rounds.
. Since this is greater than pin, no further distillation is required. The absolute volume of the d = 19 top level and 15 d = 9 second level distillation structures is 3.1 × 107 qubits-rounds.
In practice, the computation of the previous paragraph is performed for a range of values of  and the value leading to minimum volume chosen. Table I contains the minimum volumes in qubits-rounds for the range of input and output error rates of interest. Our goal is to improve these numbers using block code state distillation. Italicized entries indicate input-output parameters for which block code state distillation failed to reduce the overhead.
and the value leading to minimum volume chosen. Table I contains the minimum volumes in qubits-rounds for the range of input and output error rates of interest. Our goal is to improve these numbers using block code state distillation. Italicized entries indicate input-output parameters for which block code state distillation failed to reduce the overhead.
Given values of pin and pout, we can choose an arbitrary value of k and  for a top level of block code state distillation and calculate the required block input error rate
for a top level of block code state distillation and calculate the required block input error rate  . Concatenated 15-to-1 distillation will then be used to reduce pin to pk. The geometric volume of block code state distillation is 96k + 216. We must therefore choose a top level code distance sufficiently large to satisfy
. Concatenated 15-to-1 distillation will then be used to reduce pin to pk. The geometric volume of block code state distillation is 96k + 216. We must therefore choose a top level code distance sufficiently large to satisfy  . Given the absolute volume Vb of the block code used and the absolute volume V15 of each 15-to-1 concatenated structure used to produce an input to the block code stage, the total absolute volume assigned to each output will be (Vb + (3k + 8)V15)/k.
. Given the absolute volume Vb of the block code used and the absolute volume V15 of each 15-to-1 concatenated structure used to produce an input to the block code stage, the total absolute volume assigned to each output will be (Vb + (3k + 8)V15)/k.
The minimum absolute volume found for arbitrary k and  is shown in Table II. Italicized volumes are lower than the corresponding concatenated 15-to-1 volumes (and two-level block code distilled volumes to be discussed shortly). In all cases, the volume reduction is less than a factor of three and was typically a factor of two for the cases in which a reduction was observed at all. Note that a reduction is observed when concatenated 15-to-1 distillation needs an additional level (bold entries in Table I). This makes sense, as when just a little more distillation is required, it is better to use the lower overhead block code approach.
is shown in Table II. Italicized volumes are lower than the corresponding concatenated 15-to-1 volumes (and two-level block code distilled volumes to be discussed shortly). In all cases, the volume reduction is less than a factor of three and was typically a factor of two for the cases in which a reduction was observed at all. Note that a reduction is observed when concatenated 15-to-1 distillation needs an additional level (bold entries in Table I). This makes sense, as when just a little more distillation is required, it is better to use the lower overhead block code approach.
Continuing similarly, we constructed Table III assuming two top levels of block code state distillation. Note that errors can be correlated in the output of a single instance of block code state distillation, so with two levels of distillation one would arrange the topological structures in two orthogonal layers so that outputs from the first layer go into distinct block codes state distillation structures in the second layer. This is discussed in more detail in23,24. We found the minimum volume varying  , k1 and k2, where k1 and k2 are the k values of the first and second layers of block distillation, respectively. Where further improvement was observed, this was typically quite modest, usually less than a factor of two.
, k1 and k2, where k1 and k2 are the k values of the first and second layers of block distillation, respectively. Where further improvement was observed, this was typically quite modest, usually less than a factor of two.
Discussion
We have presented an explicit extendable topological structure corresponding to computation in the surface code that implements the block code state distillation procedure of23. Every effort was made to make this topological structure as compact as possible using available techniques29. Despite this, we found only a modest overhead reduction, on average a factor of two to three, when using block code state distillation for favorable parameters. Parameter ranges were found in which block code state distillation leads to higher overhead.
At first, it may seem surprising that (3k + 8)-to-k distillation is not universally better than 15-to-1 distillation and that the advantage, when observed, is so modest. However, 15-to-1 reduces the error by far more, taking p to 35p3, whereas (3k + 8)-to-k only takes p to (3k + 1)p2. Furthermore, the overhead per 15-to-1 output is 192 plumbing pieces, versus our current best block code structure which uses (96k + 216)/k plumbing pieces per output, which is not massively less. These properties, when the appropriate code distance is chosen at each level, particularly when one keeps in mind that larger values of k lead to larger topological structures that require larger code distances, lead to the 15-to-1 approach having lower asymptotic overhead than (3k + 8)-to-k for all values of k. Block code state distillation is therefore only useful when one has first used 15-to-1 and not quite reached the target output error rate, with only a small amount of additional distillation required. When 15-to-1 gets you just below the target output error rate, block code state distillation at present offers no advantages.
Even if one ignores the cost of Clifford gates and only considers the cost of magic states, the analysis in23 shows that block codes are not the most efficient choice for the early rounds of distillation. The numerical results therein show that a hybrid scheme of 15-to-1 distillation followed by block codes leads to optimal performance for output error 10−12, though the performance improvement over a concatenated 15-to-1 protocol is only about a factor of two or three, which is consistent with our results.
Two research directions will be explored to further reduce the overhead of state distillation. Firstly, block codes of distance higher than two and secondly, more advanced methods of compressing the complex and extendable encoding circuitry of block codes.
Methods
Block code state distillation
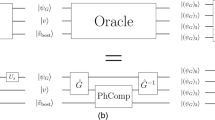
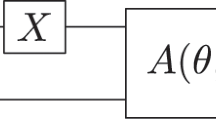
The state we are interested in distilling is  . An extendable quantum circuit taking 3k + 8 copies of |A〉, each with probability p of error and producing k copies, each with probability approximately (3k + 1)p2 of error23, is shown in Figures 1–2. The T = exp(−iπ/8σz) gate application is delayed using the circuit of Figure 2a. This circuit has the additional advantage of eliminating X errors from the T gate, leaving us only needing to detect Z errors. X and Z stand for Pauli σx and σz, respectively. Each T gate consumes one |A〉 state as shown in Figure 2b. All output states are discarded if any errors are detected. Figure 1 has been designed to detect a Z error during any single T gate. All other quantum gates are assumed to be perfect, or at least sufficiently reliable that the probability of error from gate failure is negligible compared to the probability of error from multiple T gate errors. The first order probability that the outputs will be rejected is therefore approximately (3k + 8)p, with this expression being approximate due to the ability of Figure 2b to introduce S errors and the ability of Figure 2a to filter out everything except Z errors. First order expressions are appropriate as we restrict ourselves to (3k + 8)p ≪ 1.
. An extendable quantum circuit taking 3k + 8 copies of |A〉, each with probability p of error and producing k copies, each with probability approximately (3k + 1)p2 of error23, is shown in Figures 1–2. The T = exp(−iπ/8σz) gate application is delayed using the circuit of Figure 2a. This circuit has the additional advantage of eliminating X errors from the T gate, leaving us only needing to detect Z errors. X and Z stand for Pauli σx and σz, respectively. Each T gate consumes one |A〉 state as shown in Figure 2b. All output states are discarded if any errors are detected. Figure 1 has been designed to detect a Z error during any single T gate. All other quantum gates are assumed to be perfect, or at least sufficiently reliable that the probability of error from gate failure is negligible compared to the probability of error from multiple T gate errors. The first order probability that the outputs will be rejected is therefore approximately (3k + 8)p, with this expression being approximate due to the ability of Figure 2b to introduce S errors and the ability of Figure 2a to filter out everything except Z errors. First order expressions are appropriate as we restrict ourselves to (3k + 8)p ≪ 1.
For k = 2 + 4j, the block code has the property that transversal S†X implements logical SX on each encoded logical qubit. Each logical qubit is prepared in |A〉 and hence in the absence of errors the multiple |A〉 block code will be in the +1 eigenstate of transversal S†X = T†XT. The top qubit of Figure 1 should therefore report +1, with all output discarded if −1 is reported. This single measurement is sufficient to detect a single Z error during the first two layers of T gates.
The block code has four stabilizers, specifically X0X2X3 … Xk+2, X1X2 … Xk+1Xk+3, Z0Z2Z3 … Zk+2 and Z1Z2 … Zk+1Zk+3. Detecting a Z error in the final layer of T gates involves using the stabilizers X0X2X3 … Xk+2 and X1X2 … Xk+1Xk+3. For arbitrary encoded logical states, in the absence of errors, the block code will be in the +1 eigenstate of these stabilizers. If the products of the individual X basis measurements comprising these stabilizers are not both +1, all output is discarded.
Assuming the above three checks are passed, all output is accepted, with byproduct Z operators noted as follows. For each encoded logical qubit 0 ≤ n < k, the associated logical X operator takes the form Xn+2Xk+2Xk+3. If the product of these measurements is −1, a byproduct Z is associated with output n.
References
Bravyi, S. & Kitaev, A. Universal quantum computation with ideal Clifford gates and noisy ancillas. Phys. Rev. A 71, 022316 (2005). Quant-ph/0403025.
Reichardt, B. W. Quantum Universality from Magic States Distillation Applied to CSS Codes. Quant. Info. Proc. 4, 251 (2005). Quant-ph/0411036.
Shor, P. W. Scheme for Reducing Decoherence in Quantum Computer Memory. Phys. Rev. A 52, R2493 (1995).
Laflamme, R., Miquel, C., Paz, J. P. & Zurek, W. H. Perfect Quantum Error Correcting Code. Phys. Rev. Lett. 77, 198 (1996). Quant-ph/9602019.
Bacon, D. Operator quantum error-correcting subsystems for self-correcting quantum memories. Phys. Rev. A 73, 012340 (2006). Quant-ph/0506023.
Knill, E. Quantum Computing with Realistically Noisy Devices. Nature 434, 39 (2005). Quant-ph/0410199.
Fujii, K. & Yamamoto, K. Topological One-Way Quantum Computation on Verified Logical Cluster States. Phys. Rev. A 82, 060301(R) (2010). ArXiv:1008.2048.
Steane, A. M. Multiple Particle Interference and Quantum Error Correction. Proc. R. Soc. Lond. A 452, 2551–2576 (1996). Quant-ph/9601029.
Bravyi, S. B. & Kitaev, A. Y. Quantum codes on a lattice with boundary. quant-ph/9811052 (1998).
Dennis, E., Kitaev, A., Landahl, A. & Preskill, J. Topological quantum memory. J. Math. Phys. 43, 4452–4505 (2002). Quant-ph/0110143.
Bombin, H. & Martin-Delgado, M. A. Topological Quantum Distillation. Phys. Rev. Lett. 97, 180501 (2006). Quant-ph/0605138.
Raussendorf, R. & Harrington, J. Fault-Tolerant Quantum Computation with High Threshold in Two Dimensions. Phys. Rev. Lett. 98, 190504 (2007). Quant-ph/0610082.
Raussendorf, R., Harrington, J. & Goyal, K. Topological fault-tolerance in cluster state quantum computation. New J. Phys. 9, 199 (2007). Quant-ph/0703143.
Ohzeki, M. Accuracy thresholds of topological color codes on the hexagonal and square-octagonal lattices. Phys. Rev. E 80, 011141 (2009). ArXiv:0903.2102.
Katzgraber, H. G., Bombin, H., Andrist, R. S. & Martin-Delgado, M. A. Topological color codes on Union Jack lattices: A stable implementation of the whole Clifford group. Phys. Rev. A 81, 012319 (2010). ArXiv:0910.0573.
Bombin, H. Clifford Gates by Code Deformation. New J. Phys. 13, 043005 (2011). ArXiv:1006.5260.
Bombin, H. Topological Subsystem Codes. Phys. Rev. A 81, 032301 (2010). ArXiv:0908.4246.
Fowler, A. G. 2-D color code quantum computation. Phys. Rev. A 83, 042310 (2011). ArXiv:0806.4827.
Fowler, A. G., Mariantoni, M., Martinis, J. M. & Cleland, A. N. Surface codes: Towards practical large-scale quantum computation. Phys. Rev. A 86, 032324 (2012). ArXiv:1208.0928.
Bombin, H. & Martin-Delgado, M. A. Topological Computation without Braiding. Phys. Rev. Lett. 98, 160502 (2007). Quant-ph/0610024.
Bonesteel, N. E. & DiVincenzo, D. P. Quantum Circuits for Measuring Levin-Wen Operators. Phys. Rev. B 86, 165113 (2012). ArXiv:1206.6048.
Bravyi, S. & Haah, J. Magic state distillation with low overhead. Phys. Rev. A 86, 052329 (2012).
Jones, N. C. Multilevel distillation of magic states for quantum computing. Phys. Rev. A 87, 042305 (2013).
Meier, A. M., Eastin, B. & Knill, E. Magic-state distillation with the four-qubit code. arXiv:1204.4221 (2012).
Devitt, S. J. et al. Architectural design for a topological cluster state quantum computer. New. J. Phys. 11, 083032 (2009). ArXiv:0808.1782.
Amini, J. M. et al. Scalable ion traps for quantum information processing. New J. Phys. 12, 033031 (2010). ArXiv:0909.2464.
Jones, N. C. et al. Layered architecture for quantum computing. Phys. Rev. X 2, 031007 (2012). ArXiv:1010.5022.
Kumph, M., Brownnutt, M. & Blatt, R. Two-Dimensional Arrays of RF Ion Traps with Addressable Interactions. New J. Phys. 13, 073043 (2011). ArXiv:1103.5428.
Fowler, A. G. & Devitt, S. J. A bridge to lower overhead quantum computation. arXiv:1209.0510 (2012).
Fowler, A. G. Time-optimal quantum computation. arXiv:1210.4626 (2012).
Fowler, A. G., Whiteside, A. C., McInnes, A. L. & Rabbani, A. Topological code Autotune. Phys. Rev. X 2, 041003 (2012). ArXiv:1202.6111.
Acknowledgements
A.G.F. acknowledges support from the Australian Research Council Centre of Excellence for Quantum Computation and Communication Technology (project number CE110001027), with support from the US National Security Agency and the US Army Research Office under contract number W911NF-08-1-0527. Supported by the Intelligence Advanced Research Projects Activity (IARPA) via Department of Interior National Business Center contract number D11PC20166. S.J.D. is supported in part through the Quantum Cybernetics (MEXT) and FIRST projects, Japan. The U.S. Government is authorized to reproduce and distribute reprints for Governmental purposes notwithstanding any copyright annotation thereon. Disclaimer: The views and conclusions contained herein are those of the authors and should not be interpreted as necessarily representing the official policies or endorsements, either expressed or implied, of IARPA, DoI/NBC, or the U.S. Government.
Author information
Authors and Affiliations
Contributions
A.G.F. conceived the idea, C.J. constructed the original protocol and circuits for block code state distillation. S.J.D. and A.G.F. constructed the topological versions of the circuit and wrote the manuscript. All authors contributing to editing of the final draft.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Electronic supplementary material
Supplementary Information
Surface code implementation of block code state distillation
Rights and permissions
This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivs 3.0 Unported License. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-nd/3.0/
About this article
Cite this article
Fowler, A., Devitt, S. & Jones, C. Surface code implementation of block code state distillation. Sci Rep 3, 1939 (2013). https://doi.org/10.1038/srep01939
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep01939
This article is cited by
-
Erasure conversion for fault-tolerant quantum computing in alkaline earth Rydberg atom arrays
Nature Communications (2022)
-
Real-time processing of stabilizer measurements in a bit-flip code
npj Quantum Information (2020)
-
Roads towards fault-tolerant universal quantum computation
Nature (2017)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.



 .
.





