Surface code implementation of block code state distillation

Abstract

State distillation is the process of taking a number of imperfect copies of a particular quantum state and producing fewer better copies. Until recently, the lowest overhead method of distilling states produced a single improved |A〉 state given 15 input copies. New block code state distillation methods can produce k improved |A〉 states given 3k + 8 input copies, potentially significantly reducing the overhead associated with state distillation. We construct an explicit surface code implementation of block code state distillation and quantitatively compare the overhead of this approach to the old. We find that, using the best available techniques, for parameters of practical interest, block code state distillation does not always lead to lower overhead, and, when it does, the overhead reduction is typically less than a factor of three.

Introduction

One of the grand challenges of 21st-century physics and engineering is to construct a practical large-scale quantum computer. One of the primary ways theoretical research can reduce the magnitude of this challenge is to devise ways of performing a given quantum computation using fewer qubits and quantum gates while simultaneously leaving all other engineering targets unchanged.

State distillation^1,2 is a procedure required by the majority of concatenated quantum error correction (QEC) schemes^3,4,5,6,7, with the exception of the Steane code⁸ and required by the majority of topological QEC schemes^{9,10,11,12,13,14,15,16,17,18,19}, with the exception of a 3-D color code²⁰ and a non-Abelian code²¹. As such, the search for lower overhead methods of implementing state distillation is of great importance.

Two recent works^22,23 are of particular note, both independently proposing block code based methods taking 3k + 8 imperfect copies of a particular state and distilling k improved copies. These works built on the approach of²⁴. However, in all cases, a detailed analysis of the overhead in terms of qubits and quantum gates was not performed. In this work, we explicitly construct a surface code¹⁹ implementation of one of these block code state distillation methods²³. Given a quantum computer consisting of a 2-D array of qubits with nearest neighbor interactions^25,26,27,28, there is compelling evidence that the surface code is the lowest overhead code achievable²⁹. Furthermore, this code can be used to achieve time-optimal quantum computation³⁰. The surface code therefore provides an excellent framework to gauge the cost of the new block code state distillation methods.

The discussion shall be organized as follows. We first illustrate a quantum circuit that can be used to perform block code state distillation. Next we perform a detailed comparison of the overhead of concatenated 15-to-1 and block code state distillation. We then summarize our results and discuss further work.

Results

Block code state distillation

Figure 1 illustrates a quantum circuit to implement the block code state distillation protocol of Jones²³. This protocol uses a delayed application of T gates to eliminate X errors as illustrated in Figure 2. Details of the state distillation protocol can be found in the methods section.

Figure 1

Extendable quantum circuit for block code state distillation.

This circuit takes 3k + 8 copies of |A〉, each with probability p of error and producing k copies, each with approximate probability (3k + 1)p² of error. In the figure, k = 4. The repeating unit cell is highlighted. Note that k must be even. A box encircles output numbers. Each T gate consumes one |A〉 state as shown in Figure 2.

Figure 2

Circuit identities for application of T gates.

(a) Circuit useful for delaying the application of T and eliminating X errors. (b) Circuit implementing a T gate using an ancilla state .

In Figure 3 we show a rearranged version of Figure 1 that is more convenient for physical implementation. A surface code CNOT is shown in Figure 4^12,13,19. This topological structure can be arbitrarily deformed without changing the computation it implements. This permits direct implementation of the bent CNOTs (Figure 5). This can be compressed to Figure 6. See the supplementary material for a step-by-step description of the compression process and larger versions of these figures.

Figure 3

Constant depth extendable circuit implementing block code state distillation.

This example takes (3k + 8)-to-k state distillation for k = 4. Boxes encircle output numbers. Using the surface code, bent CNOTs can be implemented exactly as shown (see Figure 5). The repeating unit cell is highlighted.

Figure 4

CNOT circuits in the surface code.

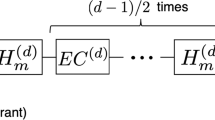
(a) CNOT quantum circuit example. (b) Equivalent surface code CNOT^12,13,19. Time runs from left to right. The scale of the figure is set by the code distance d. Small cubes are d/4 a side. Longer blocks have length d. Each unit of d in the temporal direction represents a round of error detection. Each unit of d in the two spatial directions represents two qubits. The structures are called defects and represent space-time regions in which error detection has been turned off.

Figure 5

Depth 31 canonical surface code implementation of block code state distillation.

This structure is a direct mapping of Figure 3. A larger version of this figure can be found in the supplementary material.

Figure 6

Depth 12 compressed surface code implementation block code state distillation.

A compressed version of of Figure 3. A larger version of this figure can be found in the supplementary material, along with step-by-step images explaining how it was obtained.

Overhead comparison

Suppose we desire logical |A〉 states with error p_out and can prepare logical |A〉 states with error p_in. We will consider values p_in = 10⁻², 10⁻³ and 10⁻⁴, as this covers the plausibly achievable range given the current state of quantum technology and values p_out = 10⁻⁵, …, 10⁻²⁰, as this covers essentially the entire range that could forseeably be useful in a practical quantum algorithm.

The process of preparing arbitrary logical states is called state injection and in the surface code approximately 10 gates are required to work before error protection is available¹⁹. It is therefore reasonable to assume the physical gate error rate p_g is an order of magnitude less than p_in. The logical error rate per round of error detection in a square patch of surface code as a function of p_g and code distance d is shown in Figure 7³¹.

Figure 7

Failure rates for the surface code.

Shown here is the probability p_L of logical X error per round of surface code error correction for various code distances d and physical gate error rates p_g. The asymptotic curves (dashed lines) are quadratic, cubic, quartic for distances d = 3, 5, 7 respectively.

Focusing initially on the simpler 15-to-1 concatenated distillation process, the topological structure required for a single level of distillation is shown in Figure 8. Dark structures are called dual defects, light structures are called primal defects. The geometric volume of the structure can be defined as the number of primal cubes in a minimum volume cuboid containing the structure. In this case, the structure is 6 cubes high, 16 cubes wide and 2 cubes deep, for a total V = 192. Each primal cube has dimensions d/4, each longer prism has length d. Each unit of d in the temporal direction (up in Figure 8) corresponds to a round of surface code error detection, each unit of d in the two spatial directions corresponds to two qubits. It is therefore straightforward to convert the geometric volume to an absolute volume in units of qubits-rounds. A fragment of the complete structure of edge length 5d/4 with a primal cube potentially centered within it is called a plumbing piece. Geometric volume is therefore in units of plumbing pieces. In order to calculate the overhead of state distillation, we will need to first reasonably upper bound the probability of logical error per plumbing piece.

Figure 8

Standard 15-1 state distillation in the surface code.

State distillation method taking 15 input |A〉 states, each with error p and producing with probability 1 − 15p a single output |A〉 state with error 35p^{3 1,29}. Each unit of d in the temporal direction (up in this figure) corresponds to a round of surface code error detection, each unit of d in the two spatial directions corresponds to two qubits.

Consider a forest of straight, d separated parallel defects of circumference d, as shown in Figure 9. Each defect can be assumed responsible for logical errors connecting it to two of its neighboring defects and also self encircling logical errors. The probability of each of these types of logical error per round of error detection can be upper bounded by the probability of logical error per round of error detection of a square surface. There are more potential logical errors per round connecting opposing boundaries in a square surface of distance d than there are connecting distinct defects or encircling a single defect.

Figure 9

Defect arrangement for the surface code.

A forest of d separated straight defects of circumference d. Two square surfaces of dimension d × d have been included. The logical error rate of these surfaces upper bounds the probability of a logical error connecting neighboring defects and encircling a single defect. Time runs vertically. In the temporal direction, each unit of d represents a round of error detection. In the spatial directions, each unit of d represents two qubits.

Given the per round probability of logical error p_L(d, p_g) of a square surface, we can upper bound the logical error rate of a plumbing piece P_L(d,p_g) by 2 × 3 × 5d/4 × p_L(d,p_g), where the factor of 5d/4 is for the number of rounds of error detection in a plumbing piece, the factor of 3 is for the number of distinct classes of logical error and the factor of 2 is due to the fact that a single plumbing piece can contain both a primal and a dual defect. From Figure 7, p_L(d,p_g) ~ 0.1(100p_g)^(d+1)/2, implying P_L(d,p_g) ~ d(100p_g)^(d+1)/2.

Given input error rate p_in, with 15-to-1 state distillation the output error rate can be made arbitrarily close to p_dist = 35p³ by using a sufficiently large d to eliminate logical errors during distillation. However, logical errors do not need to be completely eliminated and we define to be the amount of logical error introduced. For , the logical circuitry introduces as much error as distillation fails to eliminate and . We shall assume that logical failure anywhere during distillation leads to the output being incorrect and accepted.

Let us consider a specific example. Suppose p_in = 10⁻³, our desired p_out = 10⁻¹⁵ and our chosen . Our top level of state distillation must therefore have a probability of logical error no more than . Given V = 192 for 15-to-1 state distillation, this means we need VP_L(d,p_g) = 192P_L(d,10⁻⁴) < 5 × 10⁻¹⁶, implying d = 19. The states input to the top level of distillation must have an error rate no more than . Since this is less than p_in, more state distillation is required. Our second level of state distillation must have a probability of logical error no more than , implying d = 9. The states input to the second level of distillation must have an error rate no more than . Since this is greater than p_in, no further distillation is required. The absolute volume of the d = 19 top level and 15 d = 9 second level distillation structures is 3.1 × 10⁷ qubits-rounds.

In practice, the computation of the previous paragraph is performed for a range of values of and the value leading to minimum volume chosen. Table I contains the minimum volumes in qubits-rounds for the range of input and output error rates of interest. Our goal is to improve these numbers using block code state distillation. Italicized entries indicate input-output parameters for which block code state distillation failed to reduce the overhead.

Table 1 Minimum achieved volumes in qubits-rounds for all combinations of p_in and p_out of interest when using concatenated 15-to-1 state distillation. The approximate two orders of magnitude volume ratio of p_in = 10⁻² and 10⁻⁴ for p_out = 10⁻²⁰ is due to the former requiring three levels of distillation of distance 13, 21 and 45 respectively, whereas the latter requires just two levels of distance 7 and 15 respectively. This is directly related to the assumption that the gate error rate p_g is p_in/10, meaning much smaller distances and hence volumes, are required to achieve a given reliability. Bold numbers indicate a transition to more levels of distillation. For p_in = 10⁻², two levels are required even for p_out = 10⁻⁵, with a transition to three levels at p_out = 10⁻¹². For lower p_in, only one or two levels are required. Italicized entries are smaller than their corresponding entries in Table II and Table III

Given values of p_in and p_out, we can choose an arbitrary value of k and for a top level of block code state distillation and calculate the required block input error rate . Concatenated 15-to-1 distillation will then be used to reduce p_in to p_k. The geometric volume of block code state distillation is 96k + 216. We must therefore choose a top level code distance sufficiently large to satisfy . Given the absolute volume V_b of the block code used and the absolute volume V₁₅ of each 15-to-1 concatenated structure used to produce an input to the block code stage, the total absolute volume assigned to each output will be (V_b + (3k + 8)V₁₅)/k.

The minimum absolute volume found for arbitrary k and is shown in Table II. Italicized volumes are lower than the corresponding concatenated 15-to-1 volumes (and two-level block code distilled volumes to be discussed shortly). In all cases, the volume reduction is less than a factor of three and was typically a factor of two for the cases in which a reduction was observed at all. Note that a reduction is observed when concatenated 15-to-1 distillation needs an additional level (bold entries in Table I). This makes sense, as when just a little more distillation is required, it is better to use the lower overhead block code approach.

Table 2 Minimum achieved volumes in qubits-rounds for all combinations of p_in and p_out of interest when using a top level of block code state distillation followed by concatenated 15-to-1 state distillation. Bold numbers indicate a transition to more levels of distillation. For p_in = 10⁻², two levels, one block and one 15-to-1, are required even for p_out = 10⁻⁵, with a transition to two levels of 15-to-1 at p_out = 10⁻⁹. For lower p_in, initially no 15-to-1 distillation is required. Italicized entries are smaller than their corresponding entries in Table I and Table III

Continuing similarly, we constructed Table III assuming two top levels of block code state distillation. Note that errors can be correlated in the output of a single instance of block code state distillation, so with two levels of distillation one would arrange the topological structures in two orthogonal layers so that outputs from the first layer go into distinct block codes state distillation structures in the second layer. This is discussed in more detail in^23,24. We found the minimum volume varying , k₁ and k₂, where k₁ and k₂ are the k values of the first and second layers of block distillation, respectively. Where further improvement was observed, this was typically quite modest, usually less than a factor of two.

Table 3 Minimum achieved volumes in qubits-rounds for all combinations of p_in and p_out of interest when using two top levels of block code state distillation followed by concatenated 15-to-1 state distillation. Bold numbers indicate a transition to more levels of distillation. For all values of p_in, the first entry corresponds to no 15-to-1 distillation. Italicized entries are smaller than their corresponding entries in Table I and Table II

Discussion

We have presented an explicit extendable topological structure corresponding to computation in the surface code that implements the block code state distillation procedure of²³. Every effort was made to make this topological structure as compact as possible using available techniques²⁹. Despite this, we found only a modest overhead reduction, on average a factor of two to three, when using block code state distillation for favorable parameters. Parameter ranges were found in which block code state distillation leads to higher overhead.

At first, it may seem surprising that (3k + 8)-to-k distillation is not universally better than 15-to-1 distillation and that the advantage, when observed, is so modest. However, 15-to-1 reduces the error by far more, taking p to 35p³, whereas (3k + 8)-to-k only takes p to (3k + 1)p². Furthermore, the overhead per 15-to-1 output is 192 plumbing pieces, versus our current best block code structure which uses (96k + 216)/k plumbing pieces per output, which is not massively less. These properties, when the appropriate code distance is chosen at each level, particularly when one keeps in mind that larger values of k lead to larger topological structures that require larger code distances, lead to the 15-to-1 approach having lower asymptotic overhead than (3k + 8)-to-k for all values of k. Block code state distillation is therefore only useful when one has first used 15-to-1 and not quite reached the target output error rate, with only a small amount of additional distillation required. When 15-to-1 gets you just below the target output error rate, block code state distillation at present offers no advantages.

Even if one ignores the cost of Clifford gates and only considers the cost of magic states, the analysis in²³ shows that block codes are not the most efficient choice for the early rounds of distillation. The numerical results therein show that a hybrid scheme of 15-to-1 distillation followed by block codes leads to optimal performance for output error 10⁻¹², though the performance improvement over a concatenated 15-to-1 protocol is only about a factor of two or three, which is consistent with our results.

Two research directions will be explored to further reduce the overhead of state distillation. Firstly, block codes of distance higher than two and secondly, more advanced methods of compressing the complex and extendable encoding circuitry of block codes.

Methods

Block code state distillation

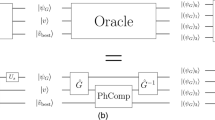
The state we are interested in distilling is . An extendable quantum circuit taking 3k + 8 copies of |A〉, each with probability p of error and producing k copies, each with probability approximately (3k + 1)p² of error²³, is shown in Figures 1–2. The T = exp(−iπ/8σ^z) gate application is delayed using the circuit of Figure 2a. This circuit has the additional advantage of eliminating X errors from the T gate, leaving us only needing to detect Z errors. X and Z stand for Pauli σ^x and σ^z, respectively. Each T gate consumes one |A〉 state as shown in Figure 2b. All output states are discarded if any errors are detected. Figure 1 has been designed to detect a Z error during any single T gate. All other quantum gates are assumed to be perfect, or at least sufficiently reliable that the probability of error from gate failure is negligible compared to the probability of error from multiple T gate errors. The first order probability that the outputs will be rejected is therefore approximately (3k + 8)p, with this expression being approximate due to the ability of Figure 2b to introduce S errors and the ability of Figure 2a to filter out everything except Z errors. First order expressions are appropriate as we restrict ourselves to (3k + 8)p ≪ 1.

For k = 2 + 4j, the block code has the property that transversal S^†X implements logical SX on each encoded logical qubit. Each logical qubit is prepared in |A〉 and hence in the absence of errors the multiple |A〉 block code will be in the +1 eigenstate of transversal S^†X = T^†XT. The top qubit of Figure 1 should therefore report +1, with all output discarded if −1 is reported. This single measurement is sufficient to detect a single Z error during the first two layers of T gates.

The block code has four stabilizers, specifically X₀X₂X₃ … X_k+2, X₁X₂ … X_k+1X_k+3, Z₀Z₂Z₃ … Z_k+2 and Z₁Z₂ … Z_k+1Z_k+3. Detecting a Z error in the final layer of T gates involves using the stabilizers X₀X₂X₃ … X_k+2 and X₁X₂ … X_k+1X_k+3. For arbitrary encoded logical states, in the absence of errors, the block code will be in the +1 eigenstate of these stabilizers. If the products of the individual X basis measurements comprising these stabilizers are not both +1, all output is discarded.

Assuming the above three checks are passed, all output is accepted, with byproduct Z operators noted as follows. For each encoded logical qubit 0 ≤ n < k, the associated logical X operator takes the form X_n+2X_k+2X_k+3. If the product of these measurements is −1, a byproduct Z is associated with output n.