Abstract
Tumour metabolism is an outstanding topic of cancer research, as it determines the growth rate and the global activity of tumours. Recently, by combining the diffusion of oxygen, nutrients and metabolites in the extracellular environment and the internal motions that mix live and dead cells, we derived a growth law of solid tumours which is linked to parameters at the cellular level1. Here we use this growth law to obtain a metabolic scaling law for solid tumours, which is obeyed by tumours of different histotypes both in vitro and in vivo and we display its relation with the fractal dimension of the distribution of live cells in the tumour mass. The scaling behaviour is related to measurable parameters, with potential applications in the clinical practice.
Similar content being viewed by others
Introduction
Recently we derived a growth law for solid tumours1, where growth depends on the distribution of live cells in the tumour mass. The model was suggested by the results of computer simulations2 and it has been validated using data from in vitro experiments. In this model the inter-vascular micro-regions of solid tumours contain both live and dead cells and the fraction of live cells is exponentially smaller as the distance from the sources of nutrients and oxygen increases. Although the decay length λ is weakly dependent on tumour size, we found that an effective, size-independent λ works nearly as well and that λ has values mostly in the range 50–150 μm. Notably, this is also the distance from the nearest blood vessel where the interstitial pO2 assumes hypoxic and anoxic values and pH drops to acidic values in the micro-regions of vascularized tumours3 and corresponds to the typical thickness of the viable tumour cell layer around blood vessels4. Here we show how the growth law can be combined with basic metabolic parameters to yield a seemingly universal metabolic scaling law for tumours, that holds both in vitro and in vivo.
We start from the tumour growth law, that can be expressed as a differential equation for tumour volume and combines proliferation of live cells in the tumour with the gradual shrinking of dead cells1

where

is the fraction of live cells in the tumour, derived from the assumption of exponential decay of the density of live cells, so that the total volume of live cells is Va = F(V)V and where the parameter α defines the individual cell proliferation rate, while the parameter δ is the shrinking rate of dead cells. The tumour volume is proportional to x3, where x is some characteristic length of the tumour, i.e., V = Ax3. In the case of spherical tumours A = 4π/3 ≈ 4.2 and x is the tumour radius, but here we consider the possibility of departure from a spherical shape. Still, we assume that the tumour keeps roughly the same shape as it grows, so that x can be chosen as a substitute for radius, e.g., as the length of a given chord between two fixed, recognizable surface features of the tumour shape. We note that A is one of the factors that set the rate of tumour growth, at least for large tumour sizes, since in that case  and the growth term in Eq. (1) depends explicitly on A:
and the growth term in Eq. (1) depends explicitly on A:

In the context of this model, the nutrient consumption rate μ of the whole tumour is given by the number of live cells in the tumour F(V)V/vc, times the mean consumption rate per cell c

where vc is the mean tumour cell volume and η = c/vc is the mean nutrient consumption rate per cell and unit volume. We remark that Eq. (4) shows that the nutrient consumption rate interpolates between a linear behaviour

at small tumour size and a power law with exponent α = 2/3

at large tumour size (see Fig. 1).
Plot of the normalized nutrient consumption rate  (μm3) vs. tumour volume V (μm3), as given by Eq. (4) (solid line).
(μm3) vs. tumour volume V (μm3), as given by Eq. (4) (solid line).
Here we assume a spherical shape and λ = 100 μm, which is close to the values found in experimental tumour spheroids1. The dotted line is the normalized rate  from Eq. (5), while the dashed line is
from Eq. (5), while the dashed line is  from Eq. (6). The volume range corresponds to a minimum radius of 5 μm (i.e., approximately a single cell), up to a maximum of 2000 μm. The arrow marks the volume corresponding to a nearly spherical avascular tumour with a diameter of 1 mm.
from Eq. (6). The volume range corresponds to a minimum radius of 5 μm (i.e., approximately a single cell), up to a maximum of 2000 μm. The arrow marks the volume corresponding to a nearly spherical avascular tumour with a diameter of 1 mm.
At this point we stress that the rate η = c/vc is cell-type specific, while the area parameter A depends on the kind of tumour (and therefore on the cell type), on the particular tumour history and finally on the choice of the characteristic length x. These latter two dependences should normally be weak, if we assume that x is always close to the diameter of a nearly spherical shape and that the development of a given kind of tumour is roughly the same in different experimental or clinical settings.
Results
We have considered the experimental values of the normalized rate  of glucose consumption in tumour spheroids obtained from different cell lines, as well as in different histotypes of primary and metastatic human solid tumours grown in rats5,6,7,8,9,10,11,12 (see Methods). This normalization factors out the specific metabolic consumption of different cell lines. From individual fits of each data set we find that they are well described by
of glucose consumption in tumour spheroids obtained from different cell lines, as well as in different histotypes of primary and metastatic human solid tumours grown in rats5,6,7,8,9,10,11,12 (see Methods). This normalization factors out the specific metabolic consumption of different cell lines. From individual fits of each data set we find that they are well described by

where ηk is the cell-line specific consumption rate and λk and Ak are the parameter values obtained for the corresponding k-th data set. The values λk and Ak obtained in these fits are reported in 1234Table 5 in Methods and we notice that λk varies in a very limited range, while Ak differs markedly in in vitro and in vivo tumours. The specific values Ak were used to define the doubly normalized rate

where λ is an effective value of the parameter – which is justified by the limited variation found in the fits – and z = V/A. Using the redefined rate  , all individual data points
, all individual data points  (i-th experimental value of the k-th data set), from both in vitro and in vivo tumours, follow one common curve
(i-th experimental value of the k-th data set), from both in vitro and in vivo tumours, follow one common curve  , shown in Fig. 2, that depends on the effective parameter λ, which we estimate from the fit.
, shown in Fig. 2, that depends on the effective parameter λ, which we estimate from the fit.
Doubly normalized glucose consumption rate  vs. z (z = V/A).
vs. z (z = V/A).
Here we take glucose as representative of all nutrients (see Methods). The black line is a single fit of Eq. (8) to all data shown in the figure: the fit yields λ = 102 ± 2 μm and it is compatible with the values found in the analysis of growth curves of tumour spheroids1. The dotted line is the linear approximation  , Eq. (5), at small tumour size, while the dashed line is the approximation
, Eq. (5), at small tumour size, while the dashed line is the approximation  , Eq. (6), at large tumour size. Data from human tumours (green circles) include breast, uterine and ovarian carcinomas, melanomas, thyroid carcinomas, colon and lung carcinomas.
, Eq. (6), at large tumour size. Data from human tumours (green circles) include breast, uterine and ovarian carcinomas, melanomas, thyroid carcinomas, colon and lung carcinomas.
While we discuss the whole selection of data in the Methods section, here it is important to note that in the case of human tumours in vivo we must cope with the scarcity of available data. Indeed, for each data set we need the metabolic rate – i.e., rate of glucose consumption – of individual cells, their average volume and the metabolic rate of the corresponding tumours and the combined knowledge of these data is quite rare. Therefore we group the few complete data on human tumours in vivo in a single data set and this produces an additional variability which is not accounted for by the model. However, we find that the η's for different human tumours all lie within a factor 2 of their average (see the Methods section). While this adds to the fluctuations about the scaling curve, we note that log10 2 ≈ 0.3 and that the largest fluctuation about the scaling curve is about 0.4 – 0.5 as measured on the log scale of Fig. 2 and therefore we see that the largest contribution to the observed fluctuations is due to this uncertainty on the value of η. We also remark that the fluctuations are partly due to our using the same Ak for all tumours of the k-th cell line, while, strictly speaking, A is a parameter related to an individual tumour. Since the tumours in our dataset follow rather neatly the scaling curve in Fig. 2, we argue a posteriori that the contribution to fluctuations due to different A's and to different tumour environments is less than about 0.2 on the log scale of the figure – i.e., a factor smaller than 1.6 on the total tumour metabolic rate.
Even so, data points seem to follow rather nicely the predicted model behaviour and the curve of Fig. 2 provides an indirect confirmation of the validity of the growth law in real tumours. Moreover, there seem to be common mechanisms that drive the growth of solid tumours, in spite of their recognized biological differences. These mechanisms are necessarily related to parameters λ and A.
Discussion
We discuss the role of parameter λ first, starting from the remark that the volume taken by live cells is1

Eq. (9) shows that the volume of live cells scales as Va(x) ~ xD, with a size-dependent fractal dimension

and that λ determines this fractal dimension, which interpolates between D = 3 at small x and D = 2 at large x (see Fig. 3). This behaviour is not associated to any irregularity of the external tumour boundary surface, but rather to the dispersion of live cells in the tumour tissue, as viable cells are mostly concentrated close to the tumour surface in tumour spheroids or to blood vessels in vascularized tumours and gradually die away in the deeper layers1. This fractal behaviour may remind one of the nutrient distribution network of the West, Brown and Enquist13 (WBE) model, which has a fractal-like subdivision, down to a “minimum tube size” and leads to a scaling law for the basal metabolic rate of living organisms which is a power-law with exponent 3/4. However, in the case of solid tumours we do not find a single power-law, but rather a curve which interpolates between two different power-laws, Eqs. (5) and (6). Indeed, the concept of “minimum tube size” of the nutrient distribution network introduced in the WBE model13 does not apply here, since the data shown in Fig. 2 include both avascular and vascularized tumours: it is the very fine-grained fractal behaviour associated to the distribution of live cells – and therefore the value of parameter λ – that actually determines the observed metabolic scaling in the case of tumour spheroids and solid tumours.
Effective fractal dimension of the set of viable cells vs. tumour characteristic size x (μm), assuming λ = 100 μm.
The set of viable cells becomes surface-like as the tumour grows. Therefore nearly all activity is eventually confined to a thin layer between the bulk of the tumour and the nourishing medium (when in vitro), or between bulk and blood vessels (in vivo).
We already noticed in reference 1 that λ somehow summarizes the interplay of different microscopic processes – most notably, the diffusion of nutrients and toxic metabolites and the biomechanical mixing of cells – and thus the exclusive dependence of the scaling law (8) on λ seems to downplay the role of the other parameter A, which is related to the overall shape of the tumour. As remarked above, A is one of the factors that set the timescale of tumour growth and has an importance of its own, as it determines both the total tumour volume, V = Ax3 and the tumour surface area, S ≈ 3Ax2. It is also important to stress that S corresponds to the boundary between the bulk of the tumour mass and the non-cancerous environment and this includes the interface between tumour and blood vessels, even where they penetrate the tumour mass (see Fig. 4).
Schematic illustration of a vascularized tumour (not to scale).
Live cells (LC) are distributed along the tumour vasculature (TV) itself and on the tumour boundary where it is close to blood vessels in the normal tissue (NT; blood vessels in normal tissue are not shown). The value of A is determined by the interface between the bulk of the tumour and the non-cancerous environment and this includes the interface with tumour blood vessels. Areas of tumour quiescence/necrosis (N) are also shown.
In the case of highly vascularized tumours we expect to find large values for A and indeed the human tumours included in Fig. 2 yield values of A much larger than those found in avascular in vitro models (see Table 5 in Methods).
The wide-range generality of scaling law (7) – or its “doubly normalized” version (8) – is noteworthy and points to a common mechanism that drives tumour growth and bypasses the details of vascularization and the peculiarities of different histotypes. More accurate and specific experiments could establish this law with greater precision and eventually lead to a clinical scale of tumour progression from measurements of glucose consumption.
Methods
Here we provide detailed information on selection and analysis of the experimental data that we used to test the metabolic model for solid tumours. We discuss the reasons for preferring and choosing a limited set of data among the many available in the literature. Basically, this choice depends on how experimental data have been obtained and reported. Eventually, we select a list of 83 independent observations, a number that we think it is reasonably large to test model behaviour.
Issues in the selection of experimental data
In spite of the large number of available data, their usability is constrained by the following requirements:
-
the scaling law (7) holds for individual nutrients as well as for the total nutrient consumption and c depends on the specific nutrient addressed by the model as well as on the cell line. Therefore we concentrate on glucose, because glucose data are those that are more readily available.
-
The variability of tumour shape means that A is variable as well and therefore a simple fit of expression
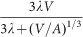
cannot determine either λ or A, but only their product λΑ. This means that we must fix the constant c/vc and this is only possible when the cell-specific parameters are known: in other words, both cell-specific data and whole-tumour growth data must be available and they must refer to the same cell line;
-
for the same reasons, we discard data expressed in arbitrary units. This rules out many data like those obtained with uncalibrated imaging techniques, those obtained with radioactive markers without any indication of the specific activity of labelled compounds and data normalized per gram of tumour tissue without any reference to the total amount of tissue used.
After an extensive search of the scientific literature, we found a limited set of data on glucose uptake in spheroids and solid tumours that fulfil these requirements. In the following we discuss the processing of these data to obtain the final dataset of 83 independent data points used to test the scaling model. We express all data in the following units: μm3 for volumes; μmol/min for the rate of glucose uptake.
While it is common to find published values of the rate of glucose uptake with its corresponding standard deviation in cell cultures, it is unusual to find more than one measurement of μ in solid tumors and often there is no estimate of its standard deviation. Thus, instead of using the straightforward error propagation formula

in most datasets we are limited to its more restricted version

where we make the minimal assumption  . We also assume that the cell volume distribution is symmetric and we take the median of vc equivalent to the average.
. We also assume that the cell volume distribution is symmetric and we take the median of vc equivalent to the average.
9L cells and spheroids – data from ref. 5
9L cells are from an established rat glioblastoma cell line. These cells form three-dimensional spheroids when grown under selective culture conditions and the data for both cultured cells and spheroids are available5; in particular we take the data from Figs. 1 and 4 in ref. 5, respectively.
The maximum reported glucose consumption by 9L cells in culture is c = 1.33 ± 0.042 pg cell−1 min−1 and the median cell volume vc = 1200 μm3, thus η = (6.15 ± 0.194)·10−12 μmol min−1 μm−3.
The glucose concentration in spheroid culture media was measured by enzymatic methods and the consumption rate was estimated by measuring glucose depletion at given time intervals. Care was taken to correct the glucose uptake due to single cells present in culture and then data were normalized per spheroid and these curated data are listed in Table 1.
Rat1-T1 and MR1 cells and spheroids – data from refs. 6,7
Rat1-T1 cells derive from T24Ha-ras-transfected rat embryo Rat1 fibroblasts and MR1 cells from myc/T24Ha-ras-co-transfected rat embryo MR1 fibroblasts. Both engineered embryo fibroblasts acquire a tumorigenic phenotype and the cells can form spheroids under appropriate culture conditions. Glucose consumption rates for these cell cultures have been measured and the data, already normalized per cell volume (i.e. η in our notation), have been reported, see Table 2 in ref. 6. The reason for data normalization stems from the careful experimental observation that the two cell types change their volumes as the consequence of the transfection with different oncogenes and thus the normalization is required for proper quantitative comparison. The rates of glucose consumptions for exponentially growing Rat1-T1 and MR1 cells are η = (3.48 ± 1.38) ·10−12 μmol min−1 μm−3 for Rat1-T1 cells and η = (8.94 ± 0.3) ·10−12 μmol min−1 μm−3 for MR1 cells.
Mean glucose turnover in Rat1-T1 and MR1 spheroids was measured photometrically by quantifying the decrease in metabolite concentration per time interval in culture media. Values of μ and σμ can be obtained from Fig. 4 in ref. 7, where they are plotted as functions of spheroid diameter (in μm) and are expressed in units of (moles of glucose uptake) s−1cell−1·10−17, i.e., on a single-cell basis. Moreover in the same paper the authors also report careful measurements of the number of live cells per spheroid and therefore the glucose rates per spheroid can be calculated as well – indeed, ref. 7 is a beautiful example of accuracy in data presentation. We take the data from Fig. 2 in ref. 7 and we fit them with the function  , where x is the spheroid diameter. The results are shown in Fig. 5 and Fig. 6. We use the estimated values of α1 and α2 to calculate the number of live cells in spheroids of given diameter and the overall glucose uptake rate per spheroid. Finally, we assume a roughly spherical spheroid shape to compute spheroid volume; the curated data are listed in Tables 2 and 3.
, where x is the spheroid diameter. The results are shown in Fig. 5 and Fig. 6. We use the estimated values of α1 and α2 to calculate the number of live cells in spheroids of given diameter and the overall glucose uptake rate per spheroid. Finally, we assume a roughly spherical spheroid shape to compute spheroid volume; the curated data are listed in Tables 2 and 3.
Human tumour cells and human primary and metastatic solid tumours – data from refs. 8,9,10,11,12
Glucose uptake rates in human solid tumours grown in vivo were measured by Kallinowski and collaborators8. In Fig. 1 of their paper, these authors report measurements carried out with a number of human primary and metastatic tumours xenografted into athymic, T-cell deficient rats. Glucose concentrations were measured enzymatically in the blood flow of perfused tumour tissues by inserting cannulas into both the supply artery and the drain vein and the kinetic decline of the metabolite concentrations in the blood before and after the tumour tissues was carefully used to compute the rates of glucose uptake by tumours.
Data are given in units of μmol of glucose per gram of wet tumour tissue per minutes and are plotted as the function of the tumour wet weight (in grams). Since the mass density of tumours is approximately 1 pg μm−3, we infer both glucose uptake rates and tumour volumes from these data. The curated data are listed in Table 4.
The human tumours studied in ref. 8 included breast, uterine and ovarian carcinomas, melanomas, thyroid carcinomas and lung carcinomas. Unfortunately, they did not investigate glucose uptake in isolated cells nor did they measure cell volumes. We have therefore mined the scientific literature for data obtained with established human carcinomas cell lines in vitro. As we shall see below, the measurements do not vary much between different cell lines and this allows us to estimate an average η value for human cells.
In Table 3 of their paper9, Mazurek et al. report the glucose consumption rates of two human breast carcinoma cell lines, MCF7 and MDA-MB-443; the values are: cMCF7 = (43.8 ± 0.5) nmol (105 cells)−1 hour−1 cMDA = (10.6 ± 0.9) nmol (105 cells)−1 hour−1. The measured volumes of MCF7 (4000 fL = 4000 μm−3) and MDA (approximately 7000 μm−3) cells can be found in refs. 10 and 11, respectively. Thus, we calculate ηMCF7 = (1.83 ± 0.01) ·10−12 μmol min−1 μm−3 and ηMDA = (2.5 ± 0.21) ·10−13 μmol min−1 μm−3.
On the other hand, Aykin-Burns et al. studied glucose consumption with human colon carcinoma cells and normal non-immortalized colon cells12. They find the following values for the three tumour cell lines HT29, SW480 and HCT116: cHT29 = (9.0 ± 1.0) μmol (106 cells)−1 day−1, cSW480 = (17.0 ± 3.0) μmol (106 cells)−1 day−1 and cHCT116 = (21.0 ± 3.0) μmol (106 cells)−1 day−1.
To the best of our knowledge, measurements of cell volume for all these cell lines are not available. However, using sensitive fluorimetric methods, Tan et al. measured and reported volume values for a number of human carcinoma cell lines, among which SW480 cells and other colon carcinoma cells14. In all cases cell volumes are close to 2 pL (i.e. 2000 μm−3) and taking this value we find ηHT29 = (3.12 ± 0.35) ·10−12 μmol min−1 μm−3, ηSW480 = (5.9 ± 1.05) ·10−12 μmol min−1 μm−3 and ηHCT116 = (7.3 ± 1.05) ·10−12 μmol min−1 μm−3.
Finally, taking into account all the above values we find the average value η = (3.68 ± 1.3) ·10−12 μmol min−1 μm−3.
Estimates of λ and A
We fit each selected experimental dataset with Eq. (7). The results are shown in Fig. 7. The corresponding values of parameters λ and A, as well as the goodness-of-fit statistics, are given in Table 5.
Data fitting
The data analysis is rather simple in this case, where data are comparatively few and the model is very smooth. To this end we used the NonlinearModelFit instruction which is built in Mathematica vs. 9.0 (Wolfram Research, Inc.).
References
Milotti, E., Vyshemirsky, V., Sega, M. & Chignola, R. Interplay between distribution of live cells and growth dynamics of solid tumours,. Sci. Rep. 2, 990, 10.1038/srep00990 (2012).
Milotti, E. & Chignola, R. Emergent properties of tumor microenvironment in a real-life model of multicell tumor spheroids. PLoS ONE 5, e13942, 10.1371/journal.pone.0013942 (2010).
Helmlinger, G., Yuan, F., Dellan, M. & Jain, R. K. Interstitial pH and pO2 gradients in solid tumors in vivo: high resolution measurements reveal al lack of correlation. Nat. Med. 3, 177–182 (1997).
Tannock, I. F. The relation between cell proliferation and the vascular system in a transplanted mouse mammary tumour. Br. J. Cancer 22, 258–273 (1968).
Li, C. K. N. The glucose distribution in 9L rat brain multicell tumour spheroids and its effect on cell necrosis. Cancer 50, 2066–2073 (1982).
Kunz-Schughart, L. A., Simm, A. & Müller-Klieser, W. Oncogene- associated transformation of rodent fibroblasts is accompanied by large morphologic and metabolic alterations. Oncol. Rep. 2, 651–661 (1995).
Kunz-Schughart, L. A., Doetsch, J., Müller-Klieser, W. & Groebe, K. Proliferative activity and tumorigenic conversion: impact on cellular metabolism in 3-D culture. Am. J. Physiol. Cell Physiol. 278, C765–C780 (2000).
Kallinowski, F. et al. Blood flow, metabolism, cellular microenvironment and growth rate of human tumor xenografts. Cancer Res. 49, 3759–3764 (1989).
Mazurek, S., Michel, A. & Eigenbrodt, E. Effect of extracellular AMP on cell proliferation and metabolism of breast cancer cell lines with high and low glycolytic rates. J. Biol. Chem. 272, 4941–4925 (1997).
Guppy, M., Leedman, P., Zu, X. L. & Russel, V. Contribution of different fuels and metabolic pathways to the total ATP turnover of proliferating MCF-7 breast cancer cells. Biochem. J. 364, 309–315 (2002).
Stoletov, K., Montel, V., Lester, R. D., Gonias, S. L. & Klemke, R. High resolution imaging of the dynamic tumor cell-vascular interface in transparent zebrafish. Proc. Natl. Acad. Sci. U.S.A. 104, 17406–17411 (2007).
Aykin-Burns, N., Ahmad, I. M., Zhu, Y., Oberley, L. W. & Spitz, G. R. Increased levels of superoxide and H2O2 mediate the differential susceptibility of cancer cells versus normal cells to glucose deprivation. Biochem. J. 418, 29–37 (2009).
West, G. B., Brown, J. H. & Enquist, B. J. A General Model for the Origin of Allometric Scaling Laws in Biology. Science 276, 122–126 (1997).
Tan, C. W. et al. Wnt signalling pathway parameters for mammalian cells. PLoS ONE 7, e31882, 10.1371/journal.pone.0031882 (2012).
Acknowledgements
The authors wish to acknowledge support from MIUR-PRIN2009 and from the HPC CASPUR Standard Grant 2011.
Author information
Authors and Affiliations
Contributions
E.M. conceived the model, analysed data and wrote the manuscript. V.V. analysed data. M.S. and R.C. searched the literature, contributed to model building and wrote the manuscript. S.S. contributed to the discussion on the role of metabolic scaling and of fractal behaviour and to a critical revision of all the text.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Rights and permissions
This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivs 3.0 Unported License. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-nd/3.0/
About this article
Cite this article
Milotti, E., Vyshemirsky, V., Sega, M. et al. Metabolic scaling in solid tumours. Sci Rep 3, 1938 (2013). https://doi.org/10.1038/srep01938
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep01938
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.






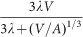

 and
and  .
.
 and
and  .
.