Abstract
Hard X-ray sources from femtosecond (fs) laser-produced plasmas, including the betatron X-rays from laser wakefield-accelerated electrons, have compact sizes, fs pulse duration and fs pump-probe capability, making it promising for wide use in material and biological sciences. Currently the main problem with such betatron X-ray sources is the limited average flux even with ultra-intense laser pulses. Here, we report ultra-bright betatron X-rays can be generated using a clustering gas jet target irradiated with a small size laser, where a ten-fold enhancement of the X-ray yield is achieved compared to the results obtained using a gas target. We suggest the increased X-ray photon is due to the existence of clusters in the gas, which results in increased total electron charge trapped for acceleration and larger wiggling amplitudes during the acceleration. This observation opens a route to produce high betatron average flux using small but high repetition rate laser facilities for applications.
Similar content being viewed by others
Introduction
Synchrotron light sources have proven their usefulness for users especially in the biological and condensed matter applications1. Moreover, some X-ray Free Electron Laser (XFEL) facilities are recently constructed and operational2, which are expected to have revolutionary impacts on science and technology. However, these machines are huge in size (km-size) and accessible to limited users. Recently with the development of ultrashort high power lasers, the laser-plasma X-rays are attracting increasing interest as compact and affordable sources with some unique features for many applications. Hard X-ray emission from femtosecond laser-produced plasmas has been extensively studied in the past years3,4,5,6,7,8,9,10,11. The source energy conversion efficiency and temporal duration have been greatly improved6,7. However, most laser-driven hard X-ray sources are spatially symmetric, except for high harmonic generation8, Thomson scattering9 and betatron radiation3. High harmonics and Thomson scattering usually suffer from their low yield.
A well-collimated X-ray beam with fs duration is produced when a relativistic laser pulse propagates in an underdense plasma: this occurs as some electrons are injected into the laser wakefield in plasma and experience transverse betatron oscillations while being accelerated forward3. Intense betatron radiation, with photon energy from keV X-rays10 to gamma-rays11, has been generated via the accelerated electrons undulating in the bubble structure of the wakefield. These oscillations occur at the betatron frequency ωβ = ωp/(2γ)1/2, where ωp is the plasma frequency and γ is the Lorentz factor of the electron beam10. The average photon number with mean energy  emitted by an electron is given by Nx = 5.6 × 10−3 NβK, where Nβ is the number of oscillation periods and K is the strength parameter of the plasma wiggler given by K = 2π(γr0)/λb = 1.33 × 10−10 γ1/2ne1/2[cm−3]r0[μm], in which r0 is the electron wiggling amplitude. Hence the characteristics of betatron X-rays are mainly determined by the accelerating electron properties, including the electron energy, beam charge, as well as the electron wiggling amplitude inside the wakefield structure. However, when using a gas target, it is usually mutually exclusive to improve both the accelerated electron energy and charge simultaneously. For example, a low plasma density is necessary for longer pump-depletion length and higher electron energy, but it also results in lower total electron charge being injected. This is the reason why the reported electron charge in most of experiments using a medium-size laser facility is limited to 100 pC. To enhance the betatron X-rays, an experiment attempted to increase the wiggling amplitude of injected electrons using an asymmetric tilted pulse front12, but it usually effects the formation of the laser wakefield and reduces the final electron energy. Therefore, in order to enhance the betatron radiation brightness, one needs to find an effective way to increase both the electron beam charge and the electron wiggling amplitude in laser acceleration, which has been the subject of many current investigations.
emitted by an electron is given by Nx = 5.6 × 10−3 NβK, where Nβ is the number of oscillation periods and K is the strength parameter of the plasma wiggler given by K = 2π(γr0)/λb = 1.33 × 10−10 γ1/2ne1/2[cm−3]r0[μm], in which r0 is the electron wiggling amplitude. Hence the characteristics of betatron X-rays are mainly determined by the accelerating electron properties, including the electron energy, beam charge, as well as the electron wiggling amplitude inside the wakefield structure. However, when using a gas target, it is usually mutually exclusive to improve both the accelerated electron energy and charge simultaneously. For example, a low plasma density is necessary for longer pump-depletion length and higher electron energy, but it also results in lower total electron charge being injected. This is the reason why the reported electron charge in most of experiments using a medium-size laser facility is limited to 100 pC. To enhance the betatron X-rays, an experiment attempted to increase the wiggling amplitude of injected electrons using an asymmetric tilted pulse front12, but it usually effects the formation of the laser wakefield and reduces the final electron energy. Therefore, in order to enhance the betatron radiation brightness, one needs to find an effective way to increase both the electron beam charge and the electron wiggling amplitude in laser acceleration, which has been the subject of many current investigations.
In this paper, we present the generation of large-charge electron beams as well as strong betatron X-rays using an Ar clustering gas jet target irradiated with a 3 TW femtosecond laser. The measured emission yield with the photon energy > 2.4 keV reaches 2 × 108 photons/shot, which is ten-fold enhancement comparing to the emission flux produced by using gas target with the same laser parameters. Experiment and simulations point to the existence of clustering in the background gas, which leads to the increased number of trapped electrons as well as much larger wiggling amplitudes during acceleration, beneficial to betatron X-ray photon emission.
Results
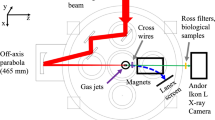
The experimental set-up is shown in Fig. 1 . Laser pulses from a 3 TW laser system at 80 fs are focused to the target center either with Ar clustering gas target or He gas target with the same plasma density (see methods). By using Ar clustering gas as an acceleration media, the X-ray photon yield of laser-driven betatron radiation is greatly enhanced in our experiment. Fig. 2(a) shows the Ar betatron X-ray profile obtained in a single laser shot with the photon energy > 2.4 keV. Compared to the X-ray profile from a gas He target with the same laser parameters, the Ar betatron emission is found to be much more intense. The emission yield reaches 2 × 108 with a confidence interval of 1.6 ~ 2.4 × 108 for a single laser shot with a divergence angle ~ 10 mrad, whereas it is < 1 × 107 in the case of the He gas target, as shown in Fig. 2(b) . This is an achievement of intense keV betatron X-rays using laser system at a few TW only. Fig. 2(c) shows the measured X-ray signal for different cut-off filters in experiment. Most of betatron X-ray photons are concentrated in the energy higher than 2.4 keV. Compared to a previous observation13 with a gas target and a 10 TW laser facility, the betatron X-ray flux at the similar X-ray photon energy (~ 3 keV) we obtained here is 400 times larger even though our laser power is 3 times lower, i.e. ~ 1000 times higher conversion efficiency is achieved compared to the previous reported results. Using a synchrotron asymptotic limit distribution model as defined in Ref. [14], the critical energy we obtained is Ecrit = hωc = 0.6 keV after minimizing the least squares fit for data obtained from experiment and the synchrotron model. It should be emphasized that the betatron X-ray yield depends critically on the laser contrast. The yield is reduced by two orders of magnitude when the laser pulse contrast decreases from 109 to 107 while fixing the laser pulse energy. Pre-expansion of a solid-density cluster by the laser pre-pulse leads to ineffective electron heating and acceleration, as described below and results in the decrease of X-ray yield produced.
The measured betatron emission characteristics: The emission beam profile obtained using 36 μm Al foil wrapped IP for Ar target (a) and He target (b), respectively.The hallow cloud signal in (a) (left side) was caused by low energy electrons bypassing the magnet. The measured (square) and modeled (triangle) X-ray signal for different filters are shown in (c). The inset shows the beam profile recorded after the cut-off filters 18 μm Al (I), 18 μm Al + 10 μm Cu (II), 18 μm Al + 20 μm Cu (III) and 18 μm Al + 30 μm Cu (IV), with different cutoff energy 2.4 keV, 3.4 keV, 4.1 keV and 6.2 keV, respectively. Modeling is based on a best fit of synchrotron spectrum with Ecrit = 0.6 keV.
The accelerated electron spectrum was measured simultaneously because it reflects the behavior of the electron wiggling that leads to betatron X-ray generation. As shown in Figs. 3(a) and 3(b) , the electron beam profiles are measured using an Al foil-wrapped imaging plate directly after the nozzle (without magnet) in the cases of an Ar clustering gas target and a pure He gas target. The beam charge reaches over 200 pC with electron energy higher than 1 MeV. It is over 50 times higher than the case of He gas with the same electron density used (2 × 1019 cm−3). We note that the divergence angle of the electron beam using Ar cluster target is ~ 17 mrad, much larger than ~ 1 mrad for the case of He gas target. It indicates that the electron is not well collimated after acceleration in the clustering case, which suggests that large betatron oscillations of electron may occur during the electron acceleration. In addition, because of the large charge observed with the Ar cluster target, the space charge effect may play some role in the early stage of electron acceleration. Figs. 3(c) and 3(d) show the spectra obtained with the same interaction conditions. A quasi-monoenergetic electron beam at the central energy about 21 MeV is obtained for the He-gas case. But in contrast, for the case of Ar cluster target, we observe a continuous spectrum with the maximum energy over the 20 MeV level. Furthermore, both the beam charge and beam divergence angle in the case of Ar cluster are much larger than the case of He gas target. This measurement is consistent with the beam profile results. It shows the clustering gas target is more suitable for obtaining high-charge electron beam acceleration, than the gas target, with larger divergence angle. We use these electron parameters to estimate the betatron X-ray radiation. The critical energy Ecrit[keV] = 5.3 × 10−24γ2ne[cm−3]r0[μm] = 0.53 keV, which is similar to our experimental fitting above. The plasma wiggler strength K = γkbr0 = 14.1 for photons with energy > 2.4 keV. For a betatron wavelength λb = (2γ)1/2λp = 44 μm, the number of betatron oscillations executed by an electron for this laser-produced ion channel N0 = cTint/λb = 22, where cTint is the interaction length which should be about 1 mm in the experiment. So, the total betatron yield with energy of 2.5 keV is: Nx ≈ 4.4 × 10−4NeN0K = 1.7 × 108. This value is in reasonable agreement with experimental detection.
Electron beam characteristics: The beam profile obtained using 18 μm Al foil wrapped IP for He target (a) and Ar target (b), respectively, with the same electron density (2 × 1019 cm−3) and the same laser parameters.The electron spectra are shown in (c) and (d) obtained after the dispersive magnet. The color scale is the same in (c) and (d).
Discussions
To further clarify the involved physics, two-dimensional (2D) fully electromagnetic particle-in-cell (PIC) simulations have been performed. Figures 4(a) and 4(b) show snapshots of the density distribution of total electrons and energetic electrons (> 10 MeV), respectively, at t = 0.43 ps for the case of a pure gas target. Small amounts of electrons are injected into the second and following wakefield wave buckets and the tightly transverse collimation of the electron beam indicates that the trapped electrons experience small oscillation amplitudes during acceleration, which is regularly observed in self-modulated laser wakefield acceleration (SM-LWFA)15. In this case, several quasi-monoenergetic electron bunches with different energies can be achieved, also shown in Fig. 4(g) (simulation) and Fig. 3(c) (experiment) of the electron spectra. However, when using a clustering gas target, the electron density distribution shows a large bow-like structure, as shown in Fig. 4(c) for the snapshot at t = 0.43 ps and the electron density exhibits serious modulation in a broad region directly following the laser pulse. A big size plasma cavity16 (~ 10 λ0) appears in the center area, which heats the most energetic electrons, as seen in Fig. 4(e). A large quantity of electrons with the charge of 300 pC is accelerated and the electron beam transverse profile becomes very broad, as shown in Figs. 4(d) and 4(f) . The total accelerated electron charge in the case of clustering gas target is seen to reach ~ 170 pc for electrons with energies > 20 MeV. However, in case of a pure gas, electron charge injected into wakefields and accelerated to the same energy is much lower. Note that during the propagation of the laser pulse in the clustering gas, the laser pulse develops a wing structure, which also leads to a wing structure in the accelerated electron beam.
Simulation results.
2D snapshots of the electron density distribution of gas (a) and clusters (c) at time of t = 140T0 (T0 is the laser optical cycle). (e) shows the electrical field in the interaction regime at the same time [corresponding to (c)] for the cluster target. The spatial distributions of the accelerated electrons at the same time are shown for the case with the gas target with energy > 10 MeV (b) and clusters with energy > 10 MeV (d) as well as > 20 MeV (f). (g) shows the electron energy spectra obtained with gas (blue line) and clusters (red line).
Our simulation results show that the direct laser acceleration (DLA)17,18 has important contribution to drive electrons with large oscillations in the case of a clustering gas target. Figure 5(a) plots some trajectories of selected electrons which are accelerated to high energy. It shows that the oscillation amplitudes increase from a center cavity quickly to 10 μm and electrons undergo wiggling at the betatron frequency ωβ, indicating a strong resonant coupling with the laser field. As a comparison, the electron transverse oscillation is very small in the case of He. In the meantime, the transverse momentum will transfer to longitudinal momentum via the v x B drift by a self-generated azimuthal magnetic field, where electrons gain energy directly from the laser. For example, in Fig. 5(b) , the energy gain of a sample electron reaches ~ 30 MeV over several betatron oscillations. It also indicates that the energy obtained from transverse electrical field is more important than that achieved from the longitudinal electrical field, also see in Fig. 5(c) . We count the total energy gain for all electrons with energy over 10 MeV. It turns out that the energy gain from DLA counts for 76% of the total energy gain. In contrast, in the case with the He pure gas target, the energy gain is mostly due to the laser wakefield acceleration (only about 1.35% of the total energy gain comes from DLA). The energy spectrum is in thermal distribution, as Fig. 4(g) shown, because of the random original acceleration phase of accelerated electrons. On the other hand, the electron oscillation amplitude as simulated (~ 10 μm) is in good agreement with that deduced from the critical energy (0.6 keV) fit to the experimental betatron X-ray spectrum, ~ 9 μm. All of the above simulation and experimental results strongly suggest the presence of DLA mechanism in the case of clustering gas target. Usually when using pure gas target, DLA will dominant over LWFA at high plasma density and very high laser intensity, i.e: when a0 = 0.89 × I1/2[1018 W cm−2]λ0[μm] ≫ 1, which always take place by using petawatt laser pulses14. However, as described in Ref. [19], when using a clustering gas target even in modest laser intensity, the strong resonant heating of cluster electrons7 in the early stage of interaction results in higher local electron density and much larger pre-acceleration phase in the transverse direction than the case of a non-clustering gas, which makes it easy to shorten the time period before strong v x B starts. As shown in Fig. 5(a) , electrons start to be heated from the very beginning of the interaction and quickly experience betatron resonant oscillations. Therefore, the clustering gas is an ideal medium to stimulate the DLA mechanism under modest laser intensity.
(a) Traced electron trajectories from simulation with a cluster target (solid line) showing transverse deflection y.Two dotted lines for the case of pure gas target are also shown for comparison. (b) A traced electron average energy versus time, where the solid red line shows the energy gained from DLA and the dashed blue line shows that from the ES field. (c) Energy gain from DLA versus that from ES field at 200 T0, where each point denotes a traced electron; here black dots are found with the Ar clustering target and red dots with the He gas target.
In summary, we have demonstrated a new method for generating intense betatron X-rays using a clustering gas target irradiated with an ultra-high contrast laser of 3 TW only. The yield of the well-collimated Ar X-ray betatron emission has been measured to be 2 × 108 photons/pulse, which is a ten-fold enhancement compared to the emission flux produced by using a normal gas target under the same laser parameters. Simulations point to the existence of clustering as a contributor to the DLA mechanism, leading to higher accelerated electron charge (x50) and much larger electron wiggling (~10 μm) amplitudes in the plasma channel, thereby finally enhancing the betatron X-ray photons. Here in this DLA regime, electrons are efficiently driven on the fs time scale, producing enhanced X-ray emission with durations about three orders of magnitude shorter than that of typical pulses produced by synchrotron sources. Together with the inferred source size of the betatron oscillation amplitude ~10 μm and 10 fs duration deduced from electron bunch length in Fig. 4(f), the peak brightness of the radiation in the energy range of about 3 keV is estimated to be ~ 5 × 1021 photons/s/mm2/mrad2/0.1%BW, which is comparable to the peak brightness of the third generation of synchrotron radiation sources. Being perfectly synchronized with the driver laser pulse, this kind of table-top, ultra-intense and spatially coherent X-ray sources with fs duration opens prospect for time-resolved “single-shot” ultrafast pump-probe applications employing phase contrast imaging, X-ray absorption fine structure and X-ray diffraction without heat-induced blurring. Moreover, a variety of other applications including imaging with high spatial resolutions may be realized with such X-ray sources at much higher photon flux produced with 0.1–1 kHz lasers.
Methods
Laser system
The experiments are carried out by using the XL-II laser facility in the Institute of Physics-CAS, which includes a 10 Hz, 300 mJ Ti:Sapphire laser working at the centre wavelength λ = 800 nm. The pulse with duration τ0 = 80 fs is focused with an f/6 off-axis parabola (OAP) onto a focal spot of size w0 = 4 ± 0.1 μm. The focal spot size was measured by a removable diagnostic system consists of a microlens and a visible CCD. In the focal region the laser average intensity is I = 3.0 × 1018 W/cm2. With the help of optical parametric chirped pulse amplification, the laser pulse contrast, compared to its ns prepulse, has been improved to 109.
Production of atomic clusters
A supersonic pulsed gas (Ar) jet is used, which is a 1.2 mm × 10 mm rectangular nozzle at the exit. With sufficiently high backing pressure, clusters are formed in the gas jet flow due to the adiabatic cooling of a gas expanding into vacuum. A probe beam is used for detecting the parameters of the clusters. According to the Hagena scaling law20, the cluster size is estimated. An average size of ~ 8 nm in diameter is estimated at a stagnation pressure of 4 Mpa, with an average plasma density of 2 × 1019 cm−3.
Diagnostics of electron and radiation
Electrons are dispersed by a strong magnet placed 20 cm after the nozzle and an imaging plate follows the magnet to record the electron beam. A filtered imaging plate is also located in the laser propagation direction to detect the X-ray flux and spatial profile with photon energy > 2.4 keV. Different filters will be placed in front of the IP (as described in Fig. 2 ) to selectively attenuate the X-ray flux and estimate the spectral content as cut-off filters14.
Particle-in-cell simulation
Numerical simulations were carried out with our PIC code KLAP 2D, where a p-polarized laser pulse is focused into a pure gas target or a cluster-gas target with a focal spot size w0 = 8 μm. The laser pulse has a transverse Gaussian shaped envelope with a peak strength a0 = 2.5, corresponding to an average intensity I = 3 × 1018 W/cm2 in the focal region. The plasma density used in simulation for He is 2 × 1019 cm−3 and for Ar surrounding gas is 1.7 × 1019 cm−3. The clusters, with a fixed density n = 1.7 × 1022 cm−3 and diameter d = 8 nm, are distributed uniformly in the background gas with a fixed gap rc = 120 nm between one another. Simulations were performed in a boosted frame moving along with the laser pulse. The size of the simulation box is 36 × 80λ02, with grid size of 0.01λ0 (9 particles per cell). To verify that electrons gain energy mainly from the laser fields rather than from the longitudinal fields, one chose some particles with final energy E > 30 MeV to trace their energy gains. According to the equation of motion for electrons, for each particle the energy gain from electrostatic field and laser field (DLA) can be obtained from EES = ∫0tExvxdt' and EDLA = ∫0tE⊥v⊥dt', respectively, where Ex and E⊥ are the normalized longitudinal and transverse electric fields, respectively21.
References
Sinha, S. L., Glyde, H., Briber, R. & Takata, M. Access to Majior Internationl Facilities,. Synchrotron Radiation News 23, 33–38 (2010).
Emma, P. et al. First lasing and operation of an ångstrom-wavelength free-electron laser,. Nat. Photon. 4, 6417 (2010).
Rousse, A. et al. Production of a keV X-ray beam from synchrotron radiation in relativistic laser-plasma interaction. Phys. Rev. Lett. 93,135005 (2004).
Tillman, C. et al. Imaging using hard X-rays from a laser-produced plasma. Appl Phys B-Lasers O 61, 333–338 (1995).
Kieffer, J. C. et al. Future of laser-based X-ray sources for medical imaging. Appl Phys B-Lasers O 74, S75–S81 (2002).
Chen, L. M. et al. Study of X-ray emission enhancement via a high-contrast femtosecond laser interacting with a solid foil. Phys. Rev. Lett. 100, 045004 (2008).
Chen, L. M. et al. Intense High-contrast femtosecond K-shell X-ray source from laser-driven Ar clusters. Phys. Rev. Lett. 104, 215004 (2010).
Spielmann, C. et al. Generation of coherent X-rays in the water window using 5-femtosecond laser pulses. Science 278, 661–664 (1997).
Schoenlein, R. W. et al. Femtosecond X-ray pulses at 0.4 angstrom generated by 90 degrees Thomson scattering: A tool for probing the structural dynamics of materials. Science 274, 236–238 (1996).
Kneip, S. et al. Bright spatially coherent synchrotron X-rays from a table-top source. Nat. Phys. 6, 980–983 (2010).
Cipiccia, S. et al. Gamma-rays from harmonically resonant betatron oscillations in a plasma wake. Nat. Phys. 7, 867–871 (2011).
Mangles, S. P. D. et al. Controlling the spectrum of X-rays generated in a laser-plasma accelerator by tailoring the laser wavefront. Appl. Phys. Lett. 95, 3258022 (2009).
Thorn, D. B. et al. Spectroscopy of betatron radiation emitted from laser produced wakefield accelerated electrons. Rev. Sci. Instr. 81, 10E325 (2010).
Kneip, S. et al. Observation of synchrotron radiation from electrons accelerated in a Petawatt-laser-generated plasma cavity. Phys. Rev. Lett. 100, 105006 (2008).
Hidding, B. et al. Generation of quasimonoenergetic electron bunches with 80-fs laser pulses. Phys. Rev. Lett. 96, 105004 (2006).
Mangles, S. P. D. et al. Electron acceleration in cavitated channels formed by a petawatt laser in low-density plasma. Phys. Rev. Lett. 94, 245001 (2005).
Pukhov, A. et al. Particle acceleration in relativistic laser channels. Phys. Plasmas 6, 2847–2854 (1999).
Gahn, C. et al. Multi-MeV electron beam generation by direct laser acceleration in high-density plasma channels. Phys. Rev. Lett. 83, 4772–4775 (1999).
Chen, L. M. et al. Emission of a hot electron jet from intense femtosecond-laser–cluster interactions. Phys. Rev. E 66, 025402 (R) (2002).
Hagena, O. F. et al. Cluster formation in expanding supersonic jets: effect of pressure, temperature, nozzle size and test gas. J. Chem. Phys. 56, 1793 (1972).
Sheng, Z. M. et al. Stochastic heating and acceleration of electrons in colliding laser fields in plasma. Phys. Rev. Lett. 88, 055004 (2002).
Acknowledgements
We thank L. T. Hudson and J. F. Seely for fruitful discussions. This work was supported by the National Basic Research Program of China (No. 2013CBA01501 and 2013CBA01504), National key Scientific Instrument and Equipment Development Project (No. 2012YQ120047) and the NSFC (No. 60878014, 10974249, 10925421, 11105217, 11121504, 11175119 and 11175192).
Author information
Authors and Affiliations
Contributions
L.M.C. proposed the research. L.M.C., W.C.Y., D.Z.L., N.H., L.Z., J.Y.M., K.H., Y.M., J.R.Z. performed the experiment. Z.D.H. and W.M.W. performed the PIC simulations. L.M.C., W.M.W., Z.M.S. and W.C.Y. analyzed the data and simulations. J.L.M. and X.L. operated the laser. L.M.C., Z.M.S. and N.H. wrote the paper. Z.Y.W., Y.T.L. and J.G. joined discussions. J.Z. supported the project.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Rights and permissions
This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivs 3.0 Unported License. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-nd/3.0/
About this article
Cite this article
Chen, L., Yan, W., Li, D. et al. Bright betatron X-ray radiation from a laser-driven-clustering gas target. Sci Rep 3, 1912 (2013). https://doi.org/10.1038/srep01912
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep01912
This article is cited by
-
The X-Ray Emission Effectiveness of Plasma Mirrors: Reexamining Power-Law Scaling for Relativistic High-Order Harmonic Generation
Scientific Reports (2020)
-
Attosecond betatron radiation pulse train
Scientific Reports (2020)
-
Gamma-ray emission from wakefield-accelerated electrons wiggling in a laser field
Scientific Reports (2019)
-
The application of near-infrared reflectance hyperspectral imaging for the detection and extraction of bloodstains
Cluster Computing (2019)
-
Ion energy spectra directly measured in the interaction volume of intense laser pulses with clustered plasma
Scientific Reports (2018)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.