Introduction

Si is a promising anode material for Li-ion batteries, since it absorbs large amounts of Li1,2. Maximum insertion of Li in Si corresponds to Li4.4Si, which possesses a theoretical Li capacity of 4200 mAh/g, an order of magnitude larger than for graphite anode1,2. However, insertion of such amount of Li is accompanied by 334% percent of volumetric expansion, which under constraint conditions leads to huge stresses that may cause fracture of LixSi anode3,4. This is one of the main reasons that prevents industrial application of Si anodes; that is why understanding of stress development and relaxation during lithiation-delithiation is of great applied and basic importance. As we will show, this problem is also related to the development of the concept of the chemical potential under nonhydrostatic (deviatoric) stresses and large strains5,6,7,8,9,10. For nanoscale anodes (nanowires, particles and films11,12,13,14), fracture is suppressed and large compositional volumetric deformations of LixSi under constrained conditions are believed to be accommodated by plastic flow5,8,15,16. All continuum approaches to stress relaxation in LixSi anodes are based on classical viscoplasticity theory5,8,15,16. However, recent atomistic calculations15 demonstrated that the yield strength of LixSi is significantly higher than the generated stresses. While atomistic simulations for crystalline materials without defects (in particular, dislocations and grain boundaries) overestimate the yield strength, this should not be the case for amorphous nanomaterial. Indeed, the same atomistic calculations15 describe well experimental data on biaxial stress relaxation in 100 nm thick Si film during lithiation-delithiation. This excludes plasticity as a major relaxation mechanism and makes current continuum approaches5,8,15,16 based on solely plasticity contradictory. The only qualitative concept15 that combines the chemical potential with stress intensity in the yield condition was neither justified and elaborated, nor checked against atomistic calculations or experiments.

Here, we suggested completely different approach that stress relaxation in LixSi anodes occurs not due to classical plasticity when the yield condition is satisfied but due to anisotropic (tensorial) compositional straining that takes place during insertion-extraction at any deviatoric stresses. We formulated a simple rate-equation for the deviatoric part of compositional deformation rate and calibrated a single kinetic constant in it. This equation supplemented by the elasticity rule describes quantitatively well known experimental and atomistic simulation data on the biaxial stress evolution during lithiation-delithiation of LixSi. While here we considered the simplest model without plasticity, in some cases (e.g., for lower (fluctuating) yield strength or larger sample) combination of anisotropic compositional expansion and classical plasticity may give even better description. Since there is not any threshold stress for relaxation, we suggested a method to reduce stresses by small oscillation in Li concentration and our predictions are in qualitative agreement with known experiments. Our development in stress-dependent kinematics of insertion-extraction lead to the necessity of conceptual revisiting of thermodynamics under general tensorial stress states and large strains. Thus, dissipation related to the insertion-extraction is introduced. Generalization of the chemical potential, μ, includes an additional contribution due to deviatoric stresses, which leads to the increase in the driving force both for insertion and extraction and to prediction of unexpected phenomena. A similar approach is applicable to large compositional deformation and stress relaxation for any material systems. Also, such an approach can be applied to other processes, like chemical reactions and melting under nonhydrostatic conditions17,18, when anisotropic (tensorial) transformation strain can be introduced and described in a similar thermodynamic way.

The contraction of tensors over one and two indices is designated as A · B and A : B; superscripts −1 and t denote inverse and transpose operations; subscript s means symmetrization of a tensor and I the unit tensor.

Results

The multiplicative decomposition of the deformation gradient, F = Fe ·Uc, into elastic and compositional parts is used; . This results in the decomposition of the deformation rate into elastic and compositional parts. Traditionally, Uc is considered as a spherical tensor describing isotropic volumetric expansion only. However, stresses can induce anisotropy of Li and Si atom distributions in order to minimize the Gibbs energy of the system and lead to tensorial Uc (Fig. 1a).

Figure 1
figure 1

(a) Anisotropic compositional deformation of LixSi during lithiation under deviatoric stresses.(b) When deviatoric stress S, applied to a sample, produces the same driving force for insertion and extraction, LixSi sample may be fluctuationally divided into two samples separated by an interface, in one of which insertion occurs and in another one extraction takes place. (c) Magnitude of Li flux versus chemical potential of Li reservoir μr under deviatoric stresses (solid line, Eq.(6)).

Full size image

It is convenient to present , where Jc = det Uc characterizes ratio of elemental stress-free volumes with concentration of Li x and zero and describes isochoric change in shape. Then with represents an additive decomposition of the compositional deformation rate into spherical and deviatoric parts that characterize change in volume and shape.

The initial part of the continuum thermodynamic derivations is given in the Method section. We start with the rate of dissipation per unit volume in the reference state Ω0 (undeformed Si) , where ρ0 is the mass density in the reference state Ω0, σ is the true Cauchy stress, is the molar volume of Si, μ is the chemical potential of Li and J = det F is the ratio of volumes in the deformed state of LixSi in the actual configuration Ω and reference state of Si in Ω0. Assume that the Helmholtz free energy per unit volume of Si in Ω0 is ψ = ψ(Ee, x) with Lagrangian elastic strain . Then the independence of of results in the elasticity rule (see, e.g., Ref. 19) and residual dissipation inequality

which can be transformed to

where p0 and S are the mean and deviatoric parts of the stress σ and Je = det Fe is the ratio of the volumes in the deformed and undeformed states of LixSi (J = JeJc). If one chooses p0 to make the parenthesis in Eq.(2) equal to zero, then inequality (2), , means that must depend on S and for isotropic amorphous materials is an isotropic function of S. To allow change in during insertion-extraction only (otherwise, it would not be a compositional strain but viscous strain), one needs to impose when . We accept the simplest expression

with the kinetic coefficient Λ(x). We assumed that is scaled with the magnitude of the rate of the volumetric compositional strain, and when . If we assumed that is proportional to rather than to , it would violate the dissipation inequality for . This means that the deformation rate is the same for insertion and extraction if Λ(x) and Jc(x) are the same for insertion and extraction. If Jc is a linear function of x, it does not introduce extra concentration dependence; otherwise, it does. In any case, the multiplier can be combined with Λ(x). A slightly better description of experimental and atomistic results from15 with Λ = const is achieved (see below) with additional multiplier in Eq.(3) than without it, which is why it is separated. It should be mentioned that Eq.(3) does not describe traditional viscous relaxation and dissipation, which can be made negligible in an infinitesimally slow process. Indeed, multiplying Eq.(3) by time increment dt, one obtains , i.e., relaxation Eq.(3) is time independent and the magnitude of the volumetric strain or concentration |x| plays a role of a time-like parameter. This is similar to the flow rule in classical elastoplasticity, which is time-independent and plastic strain plays a part of a time-like parameter. Thus, even for infinitesimally slow lithiation-delithiation, the problem is thermodynamically nonequilibrium, history-dependent and cannot be reduced to minimization of the free energy functional.

Traditionally (for ), the compositional dissipation rate is assumed to be zero, which defines an expression for the chemical potential μ. In our more general case with , we postulate

with the parameter ζ (0 ≤ ζ ≤ 1) and (assuming sign(0) = 0). Then the remaining part of Eq.(2) is zero, which defines the generalized chemical potential

Let us consider a Li reservoir with a chemical potential μr in contact with a small LixSi sample (i.e., heterogeneities of all parameters can be neglected) with the chemical potential of Li μ. Let the magnitude of the flux of Li to the sample in the reference state be described by experimentally determined function , with the size Δy of the order of magnitude of the size of a LixSi sample, Δμ = μr – μ and with mobility coefficient b. An unusual feature of Eq.(5) is that the last term due to the deviatoric stresses always increases the magnitude of the driving force, |Δμ|, for the Li transport both for insertion and extraction, i.e., it decreases μ for insertion and increases μ for the extraction. This is, however, logical, because if S represents internal stresses that appear due to volumetric change during insertion or extraction and suppress these processes, then Eq.(3) describes the relaxation of internal stresses, which should increase |Δμ|. If S represents prescribed external stresses, then they produce positive compositional work along the that also increases |Δμ|.

This, however, leads to an unusual situation for small driving forces |Δμ|, when the driving force is positive simultaneously for both insertion and extraction. Indeed, let the under hydrostatic condition LixSi sample be in thermodynamic equilibrium with the reservoir, i.e., . For simplicity shear modulus is independent of x. If we apply deviatoric stress S to the sample, according to Eq.(5), chemical potential of Li in LixSi will be reduced for and increased for by the same value, i.e., deviatoric stress produces the same driving force for insertion and extraction. Let under applied deviatoric stresses, a LixSi sample be fluctuationally divided into two samples separated by an interface and in one of them insertion occurred and in another one extraction took place (Fig. 1b). We neglect interface energy and elastic energy due to a jump in compositional transformation strain across an interface. However, chemical potential of a sample with is smaller than that for a sample with , i.e., and the chemical potential of such a heterogeneous sample is larger than the potential when the entire sample undergoes insertion. Thus, it is more probable that the system evolves in the way minimizing the chemical potential. Consequently (Fig. 1c),

Eq.(6) means that if the process leading to the minimal chemical potential (i.e., insertion) can occur, it will occur, despite the fact that the opposite process could occur faster for , but leads to higher chemical potential. Also, for , when only extraction is possible, there is a jump in flux, because is finite. This jump and corresponding jump in the chemical potential, , can be used for experimental determination of the parameter ζ.

In all atomistic simulations (see, e.g., Ref. 20), elastic moduli are calculated by considering elastic perturbation taking unloaded configuration Ωc (i.e., at Fe = I) as the reference one. It automatically assumes independence of the elasticity rule of Uc and the reference configuration. We accept the simplest expression for the free energy per unit volume of the unloaded configuration Ωc, , where ψc is the concentrational part of the free energy per unit volume in Ωc and C is the forth-rank tensor of isotropic elastic moduli. Then the elasticity rule Eq.(1) is

Note that in Ref. 8 the same expression for the elastic energy is accepted, but in the reference configuration, which leads to the equation . It differs from Eq.(7) by a factor of , which may be smaller than 1/4 because of large compositional volume change. Thus, if elasticity moduli are determined like in Ref. 20 in the unloaded configuration, utilization of the reference configuration for the elasticity rule introduces strong nonphysical dependence of the elasticity rule on compositional volume change and corresponding nonphysical contribution to the chemical potential. Note that in Ref. 8 such a discrepancy between different definitions of elastic moduli was mentioned and to some extent was taken into account by accepting that their Young's modulus is an increasing function of x (while the Young's modulus in Ref. 20 is a decreasing function of x).

Eqs.(3), (7) and F = Fe ·Uc have been applied to the problem of the biaxial stress generation and relaxation in Si film-like anode during lithiation-delithiation on the rigid substrate in the formulation similar to that in Ref. 8,15. Diffusion is considered to be fast enough so that homogeneous x and all fields are assumed. The boundary conditions are for in-plane principal components of the deformation gradient F1 = F2 = 1 and for out-of-plane principle stress component σ3 = 0. 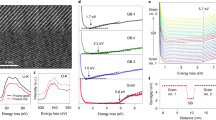The following approximations for Jc = 1+ε0 with for lithiation and for delithiation and for biaxial elastic modulus E/(1 – ν) = 127.1exp(−0.5576x) Gpa describe well experimental data and atomistic simulations in Ref. 20,21, where E and ν are the Young's modulus and Poisson's ratio. The only unknown constant Λ = 0.47GPa−1 is chosen for the best fit of biaxial stress σ1 = σ2 at x = 2 to experiment and atomistic simulations in Ref. 15. Fig. 2 demonstrates remarkable qualitative and quantitative agreements of our results for evolution σ = σ1(x) for lithiation-delithiation with experiment and atomistic simulations in Ref. 15. We could get even better agreement, if necessary, by proper fitting for Λ(x) and using different Λ(x) for lithiation and delithiation, but the main point is that agreement is good enough with just one chosen material coefficient Λ. In comparison, the viscoplastic model in Ref. 8 fits two material constants and one function (the yield strength) of x and still does not have such a good quantitative correspondence with experiments. The main reason is that the model in Ref. 8 allows for stress relaxation above the yield strength only. This underscores the importance of a conceptually correct model for stress relaxation.

Figure 2
figure 2

Calculated biaxial stress during lithiation-delithiation is in remarkable good correspondence with experimental results and density functional theory (DFT) simulations from15, with just one fitted material parameter Λ.

For delithiation, two options were used: with volumetric strain and with the same as for lithiation.

Full size image

Discussion

Since in our model there is not a threshold for the stress relaxation and it occurs both for lithiation-delithiation, one can suggest a simple method to reduce internal stresses by applying oscillatory change in x with a small magnitude, e.g., ; here is the dimensionless time and 100s is a typical diffusion time for lithium through a 100 nm silicon film15. In Fig. 3a, oscillations started after almost completion of delithiation in Fig. 2, in order to completely release stresses before some pause in the battery operation. Such a significant reduction in stresses is in qualitative agreement with experiments22. In contrast, simulation of cyclic lithiation-delithiation in Ref. 8 results in almost constant stresses. In Fig. 3b, we complete the task to keep tensile stresses below 1 GPa during delithiation by superposition of multiple oscillatory change in x, when stress reaches 1 GPa until it reduces to zero.

Figure 3
figure 3

(a) Reduction in biaxial stress with time after almost completion of delithiation (x = a in Fig. 2) under oscillatory change in x.(b) Keeping tensile stresses below 1 GPa during delithiation by superposition of multiple oscillatory change in x, when stress reaches 1 GPa until it reduces to zero (vertical lines).

Full size image

To summarize, a mechanism of stress relaxation during insertion-extraction based on the anisotropic (tensorial) compositional strain is suggested and described theoretically. Theoretical results and the suggested method to reduce stresses are in good correspondence with experiments. The general concepts of the chemical potential and dissipation due to insertion-extraction are advanced for an arbitrary material system.

Methods

The large strain continuum thermodynamic approach under general nonhydrostatic conditions is utilized. Kinematics of large deformations with multiple intermediate configurations is described in Ref. 19. Here, kinematics is based on the multiplicative decomposition of the deformation gradient into elastic and compositional parts. Compositional part includes change in volume and shape, i.e., it represents a second-rank tensor. Plastic deformation is neglected because stresses are below the yield strength. We accepted the expression for the free energy per unit volume of the unloaded configuration, which allowed us to directly use results of atomistic simulations for elastic moduli. The initial part of the continuum thermodynamic derivations is similar to that in Ref. 7,8,9,10. However, we introduce the dissipation rate due to insertion and extraction. An additional term appears in the dissipation rate due to tensorial compositional strain. Some detail are described below and in the main text.

Three configurations will be considered: the reference configuration Ω0, which corresponds to the undeformed Si state; actual configuration Ω, corresponding to the actual deformed state of LixSi and unloaded configuration Ωc, obtained after release of external stresses after deformation of LixSi without change in x. All derivations will be performed in the reference configuration Ω0. For the molar fraction of Li per mole of Si, x, the following mass balance equation is valid in Ω0

where is the molar volume of Si and j is the flux of the Li defined as a number of moles per unit reference area per unit time; ∇ and ∇· are the gradient and divergence operators in Ω0, respectively. The first and second laws of thermodynamics for the reference volume V0 for neglected volumetric forces, heat supplies and kinetic energy are:

Here v is the material velocity, h the heat flux, n is the unit normal to the external surface S0, U is the specific (per unit volume of Si) internal energy, s is the specific entropy, θ is the temperature, μ is the chemical potential of Li and P is the first nonsymmetric Piola-Kirchoff (nominal) stress tensor (the force per unit area in the undeformed state). Using the Green-Gauss theorem to transform surface to volume integrals, , as well as the equilibrium equation ∇ · P = 0, we transform Eqs.(9) and (10) to volumetric integrals and then to the local form

Combining Eq.(11) and Eq.(12) multiplied by the temperature, we obtain the dissipation inequality

Introducing the Helmholtz free energy per unit volume of Si in Ω0, ψ = U – θs; utilizing the balance Eq.(8) and stress power identity (see, e.g., Ref. 19), with the symmetric true Cauchy stress σ, deformation rate d and the volume ratio in the actual and reference configurations J = det F = dV/dV0, as well as substituting inequality (13) with three stronger inequalities, we obtain

Here we introduced the dissipation rate per unit volume in Ω0, . The isothermal version of the dissipation inequality is the initial point in the main text.