Introduction

The recent progress made in generating atomically thin graphene systems, e.g., mechanical exfoliation1 and chemical vapor deposition2,3, raised a lot of interest in researching few-layer graphene. Their electronic properties remarkably differ from those of a monolayer graphene and strongly depend on the stacking configuration and the number of layers. Bernal bilayer graphene (BBG) is one of the simplest as well as the most extensively studied few-layer graphene. BBG possesses a tiny band overlap due to the atomic interactions between two layers and thus is considered a semimetal. A perpendicular electric field can break the interlayer symmetry and open a band gap4,5. This striking characteristic was recently probed via a dual-gated transistor architecture6,7, which allows to tune the bandgap while keeping the bilayer charge neutral.

Collective Coulomb excitation is a result of electron-electron (e-e) interactions and is inherently connected to the basic electronic properties of a material. The low-frequency plasmons can not exist in an intrinsic monolayer graphene mainly due to the zero density-of-states (DOS) at the Fermi level. However, it was found that a rise in temperature and the application of a magnetic field can generate low-frequency intraband plasmons and magneto plasmons, respectively8,9. In bilayer graphene, the low-frequency plasmons evidently exist in the AA-stacked conformation, but hardly survive in the AB-stacked conformation due to the less free carriers10. Since the low-energy bands of bilayer graphene can be further modulated by a perpendicular electric field, it is worth studying the field effects on the single-particle and collective excitations. The calculation results presented in this paper predict that the field strength may control the existence, frequency and intensity of plasmons. Furthermore, these plasmons display a strong dependence on the transferred momentum.

Results

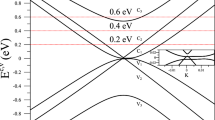
BBG owns two pairs of parabolic conduction and valence bands, as shown in Fig. 1 by the red lines (, , and ). The J2 band at high energy does not make contributions to the lowest-energy electronic excitations and thus is not a focus of our discussion. The first pair (J1), located near the chemical potential μ = 0, exhibits a very small overlap. The minimum of the subband and the maximum of the subband are located at almost the same wavevector (~ the K point). These two subbands are significantly changed by the electric field F (expressed in units of V/Å) and change from monotonic parabolic dispersions into oscillating ones. This shape has also be referred to as a “Mexican hat” in some papers. In addition to the K point, two extra band-edge states emerge along any direction. For (), there exists a band-edge state with the minimum (maximum) energy along the KΓ direction. Another band-edge state along the KM direction belongs to the saddle point. Such states are the critical points in the energy-wavevector space and thus have a high DOS. The energy difference between the lowest band-edge state of and the highest one of decides the band gap Eg, which is illustrated by the blue dashed double arrow. Eg at first grows rapidly and then slowly declines for an increasing F. At the same time, the band curvatures of the saddle points along the specified direction appear larger and those of the local extrema become smaller. The asymmetry between the conduction and the valence bands about the chemical potential is also enhanced.

Figure 1
figure 1

Energy bands.

Low-lying energy bands of BBG for different F's. The unit of F is V/Å. The blue dashed double arrow marks the energy band gap.

Full size image

During the e-e interactions, the dynamic Coulomb response will exhibit the single-particle excitations (SPEs) and collective excitations (plasmons) as the conservation of the transferred momentum (q) and energy (ω) is satisfied. These two kinds of electronic excitations are associated with each other. The e-h excitations and plasmons are, respectively, characterized by the bare response function (P(1)(q, ω)) and loss function (screened response function: ). The former directly reflecting the main features of the band structure is shown in Fig. 2. It exhibits the special structures associated with the critical points in the energy bands, which are strongly dependent on the field strength ((a)–(d)) and the transferred momentum ((e)–(h)). The imaginary parts of the polarization functions (left panels), which represent the strength of the electron-hole (e–h) excitations or the Landau damping, are related to the DOS. In a zero field, Im[P(1)] is very weak, as presented by the red lines in (a) and (c). In the presence of a field F, e.g. F = 0.4 V/Å (blue lines), a pair of discontinuous step structures and a pair of logarithmically divergent peaks clearly exist, as indicated by the vertical dotted and dashed lines, respectively. The step structures arise from the local extrema, while the logarithmically divergent peaks are derived from the saddle points. The main reason of the twin structure formation is the asymmetry of the band structures about the chemical potential and the nonidentical band slopes at both sides of the critical points. The real parts of the polarization functions (right panels) are connected with the imaginary parts by the Kramers-Krönig relations. The logarithmic peaks in Im[P(1)] correspond to the step discontinuities in Re[P(1)] and vice versa. The heights of the special structures grow with increasing F and are related to the rise in DOS or the number of excitation channels around the critical points.

Figure 2
figure 2

Polarization functions.

(a) Imaginary and (b) real parts of at q = 40 for different F′s. (c) and (d) correspond to those of , respectively. (e) – (h) are related plots at F = 0.4 for different q's. The real part of the dielectric function is shown in (i). The units of P(1) and q are eV−1Å−2 and 105/cm, respectively. The temperature is zero and the energy width due to deexcitation mechanisms is 2 meV. The vertical lines in (a) indicate the positions of special structures at F = 0.4.

Full size image

The response functions also depend on the transferred momentum Fig. 2((e)–(h)). The intensity of rises with an escalation of q; however, that of exhibits the reverse dependence. The apparent inequality between and is ascribed to charge transfer. The first pair of twin structures with the lower energy survives at large q, while the second pair is reduced to a single main structure. It is noted that, as long as the frequency larger than the energy gap, the imaginary parts of the polarization functions are nonzero at any frequencies. That implies that the plasmon and the e–h excitations will always coexist in the momentum-energy region. The feature occurs in most interband plasmons11,12,13.

The full response function is useful to determine the plasmon excitation. Fig. 2(i) shows the real part of the dielectric function. It is seen that the field causes divergent peaks, which represent the major excitation channels of , leading to two zero points in (marked with black circles). That zero point away from the peak structures (indicated by the black arrow) suffers the weaker Landau damping and may induce a plasmon excitation, i.e., a prominent peak in the loss function (Fig. 3). Assuming the equal charge distribution on the two layers (at the condition of weak field strength and small transferred momentum), the intralayer and interlayer polarization functions have the same weights, i.e., . The determinantal equation of the dielectric-function matrix (see Eq. (3)) is thus expressed as:

The plasmon mode can be obtained by setting the above equation to zero. The subtraction of the intralayer and interlayer Coulomb interactions (V11 – V12) means that the field-induced interband plasmon should belong to an anti-bonding (out-of-phase) mode14,15.

Figure 3
figure 3

Energy-loss function.

Loss spectra (a) at q = 40 for different F′s and (b) at F = 0.4 for different q's.

Full size image

The loss function, defined as , is useful for understanding the screened excitation spectra, especially the collective excitations. In a zero field, it exhibits no prominent structures because of the low density of states (red line in Fig. 3(a)). The electric field induces one prominent peak and a few weak peaks or shoulders. Those prominent peaks correspond to the zero points in with the weaker Landau damping (Fig. 2(i)). They are easily enhanced by increasing F. The prominent loss peaks may be considered as collective excitations according to their apparent polarization shifts. Such interband plasmons are similar to those in carbon nanotubes11, the π-plasmons in graphite12 and the inter-Landau-level plasmons in monolayer graphene9. Whether they could be observed in the experimental measurements is directly inferred from the peak height of the loss function. The weak peaks or shoulders, marked by triangles and crosses, have frequencies close to those of SPEs between the local extrema of and and SPEs between and ( and ) subbands, respectively. They are always obscure due to rather strong Landau damping.

These interband plasmons are strongly affected by the transferred momentum, as shown in Fig. 3 (b). The SPE frequency increases with a rising q and so does the plasmon frequency. On the other hand, the dependence of the plasmon strength on q is not monotonous. The most prominent plasmon peak becomes stronger as q increases from zero. However, when q goes through a critical momentum, it induces more e–h excitation channels between and ( and ) subbands. The enhanced Landau damping reduces the plasmon peak. This critical momentum can be raised by increasing the field strength, as shown later in Fig. 4(a).

Figure 4
figure 4

Plasmon frequencies.

Dependence of the interband plasmon frequencies and intensities (a) on momentum for different F′s and (b) on the field strength for different q's.

Full size image

The loss function discussed above is similar to the imaginary part of the trace of the full response function in other papers14,16,17,18. However, there are certain differences between their and our works. Our studies are focused on the occupied electronic states in the undoped graphenes, while the others are on the conduction carriers in the doped cases. Moreover, the other works neglect some band-structure effects when evaluating the excitation spectra. In our works, all of the energy bands with the important interlayer atomic interactions make contributions to the dynamic charge screening. Therefore, the more reliable plasmon frequencies and intensities are obtained. Since the complete energy-band effects are considered, the external electric and magnetic fields are easily added in the loss function.

There is a possibility of having collective charge fluctuations with respect to the two graphene layers due to the applied electric field similar to that in gated double-layer graphene on opposite but nominally same potential. At an extreme value of field strength, the large potential difference between layers may block the interlayer atomic interactions. In such condition, the system may be considered as two independent graphene layers (without energy-band hybridizations) and the two layers interact with each other only by interlayer Coulomb potentials. The other possible condition is that when the two graphene layers are separated far apart, the interlayer atomic interactions become neglectable. This is the case in Ref. 19. The transformation of the excitation properties from coupled layered graphene to uncoupled layered graphene is another interesting topic.

The transferred momentum and the field strength dependence of both plasmon frequency and intensity deserves a further discussion. Fig. 4(a) shows that the frequency of the prominent interband plasmon induced by a field starts at a finite value in the long wavelength limit q → 0. Therefore, it belongs to the optical plasmon mode. According to the relation between the intralayer and interlayer polarizations is negative and positive at F ≠ 0, meaning the density difference of each individual layers) and the determinantal expression discussed in Eq. (1), the charge density fluctuation in the two layers is out of phase. The plasmon frequency displays a strong dependence on the transferred momentum, which means a propagating electron wave. Increasing F can enhance the group velocity (dωp(q)/dq) at long wavelengths and prolong the lifetime. The intensity of each plasmon peak at first grows with the momentum. However, when q goes through a critical value, the frequency entering into to ( to ) excitation region, the plasmon starts to decline and finally damps out.

To induce the pronounced interband plasmon, the field strength needs to exceed a minimum value (Fig. 4(b)). This value is lowered when q gets smaller. The main reason for this reduction is a weakening of the Landau damping from the higher energy-band transitions. It is worth noting that the field-induced plasmon comes from to interband excitations and this peak is relatively weak at F → 0. Its intensity gradually grows with the increasing field strength (Fig. 4(b)), clearly indicating that the prominent plasmon peak is independent of other transition channels. The strong dependence of the plasmon mode on F and q could be further examined by inelastic light scattering spectroscopy or EELS20,21,22.

Discussion

We have considered the interlayer atomic interactions and Coulomb interactions in AB-stacked bilayer graphene to investigate the collective excitations in an electric field. Within the random-phase approximation, the dielectric function associated with the full Coulomb response is present in the tensor form (see Methods). By utilizing the dielectric function matrix, the plasmon peaks are obtained in the energy-loss function. They are collectively contributed by the interlayer and intralayer polarizations ( and ). The weight of and could be equal or unequal, which depends on the wavefunction distribution between layers. Especially, in the case of applying a perpendicular electric field, charge transfer will cause the apparent inequality between and , which is even more obvious at larger momentum. These effects and all energy bands were completely considered in our calculations.

A uniform perpendicular electric field applied to BBG dramatically alters the electronic structures and thus induces rich Coulomb excitation spectra. Energy bands are changed from monotonic parabolic dispersions into oscillating ones and a band gap opens. This causes the observed special structures in single-particle response functions, such as logarithmic peaks, discontinuous steps and twin structures. The energy-loss function is used to study the collective excitations. In zero fields, no prominent peaks exist. However, a few of interband plasmons are generated when an electric field is applied. The interband plasmons are closely related to the critical points in the energy bands and the special structures in the single-particle response functions. Their existence, frequency and strength strongly depend on the field strength and transferred momentum. The smaller the transferred momentum is, the weaker the field strength needed to trigger the plasmon peaks. The intensity of the most prominent peak always grows with an increasing field strength, while it at first increases and then declines with an increase of the transferred momentum. The strong dependence of the interband plasmons on the two realistically tunable parameters–the field strength and the transferred momentum–suggests the controllable nature of the excitation properties. This important characteristic may find application in electronics and attract more researches on stacked graphene systems.

Methods

Monolayer graphene is a honeycomb carbon lattice with two sublattices A and B. When all carbon atoms on one sheet are moved by a bond length of b = 1.42 Å along the armchair direction relative to a neighboring sheet with the interlayer distance c = 3.35 Å, BBG is obtained. Its π-electronic structure formed by the 2pz orbitals can be calculated by the tight-binding method. This method takes one intralayer atomic hopping integral, i.e., γ0 = 3.12 eV and four interlayer ones, i.e., γ1 = 0.38 eV, γ3 = 0.28 eV, γ4 = 0.12 eV and γ6 = −0.0366 eV into account23. The uniform perpendicular electric field changes the site energies on two different layers (F is the strength of an effective field due to the screening effect). The Hamiltonian built from four tight-binding functions is thus given by

where , with k being the wavevector and rj the position vector of the jth nearest-neighbor atom. Through the diagonalization of Hamiltonian matrix, the energy dispersions and the wave functions are obtained, where n is the band index and c and v respectively denotes the unoccupied and the occupied states. The wave function is the linear superposition of the periodic tight-binding functions ψlh(k), i.e., with h denoting the atom A or B and l being the layer number 1 or 2. The first Brillouin zone has the symmetry points Γ[0,0], M[2π/(3b),0] and . When the system is perturbed by a time-dependent Coulomb potential, the e-e interactions would induce screening charges and thus dominate the excitation properties. In a multilayer graphene, charges in all layers would participate in the screening process. Within RPA, the 2 × 2 dielectric-function matrix can be written as10,24:

The bare Coulomb potentials for interlayer and intralayer are Vll′(q) = vqe −q|l−l′|c, where vq = 2πe2/q. and are the intralayer and interlayer linear-bare polarzations, respectively. They are expressed as:

f(En(k)) = 1/{1+exp[(En(k)−μ(T))/(kBT)]} is the Fermi-Dirac distribution, where μ(T) is the temperature-dependent chemical potential and kB is the Boltzmann constant. δ is the energy broadening width due to various deexcitation mechanisms. The factor of 2 accounts for the spin degeneracy and the valley degeneracy is included by summing over all states in the first Brillouin zone. The interlayer polarizations (l ≠ l′) vanish when the interlayer atomic interactions are absent. The transferred momentum q is set along the ΓM direction in the calculations. The low-frequency electronic excitations hardly depend on the direction of transferred momentum.

The loss function, or the inelastic scattering probability, can be obtained through detailed calculations. It can be written as

where the effective Coulomb potential is defined as . The denominator is the average value of the external potentials on the N layers. The screened response function is used to understand the collective excitations of the low-energy π electrons.

The above dielectric-function matrix includes both interlayer atomic and interlayer Coulomb interactions and therefore is suitable to treat the excitation problems of a coupled bilayer system. A coupled bilayer graphene is different from a double-layer graphene19,25. In the latter, the interlayer atomic interactions are not taken into consideration and therefore the interlayer polarizations are absent. Since the tight-binding model incorporates the entire π-band structure, the correctness of the excitation spectrum is not constrained by the frequency. This is in contrast to results obtained by an effective-mass model and a scalar dielectric function26, for which the screening function is reliable only at very low frequencies.