Abstract
Liquid-liquid-solid transitions (LLST) are known to occur in confined liquids, exist in supercooled liquids and emerge in liquids driven from equilibrium. Molecular dynamics (MD) simulations claim many successes in forecasting the phenomena. The transitions are also studied in the framework of thermodynamics based methods and minimalistic models. In here, the proposed approach is derived in the framework of continuum and includes spatial and temporal dynamic heterogeneities; the approach is meant to capture the material behavior at small scales. We conjecture that the liquid-like and solid-like behaviors are dissimilar enough for the two to be governed by different constitutive relations. In this way, we gain additional degree of freedom, which is found essential when predicting the transitional phenomena. As a result, we derive the LLST criteria for liquids in equilibrium, during steady flow and at transient conditions. Lastly, we forecast short-lived LLSTs in human blood during cardiac cycle.
Similar content being viewed by others
Introduction
Envision a thin film of a molecular liquid exhibiting one or a combination of transitions: the liquid-liquid transition (LLT), where a semi-organized molecular structure is formed (liquid II); the liquid-solid transition (LST), in this case the liquid is transformed into a solid-like material and, lastly, the liquid-liquid-solid transition (LLST) defined as a combination of the two. When controlled, these transitions can be utilized in micro-electro-mechanical systems (MEMS), joint lubrication in biology and in micro-fluidics. Suspensions exhibit similar behaviors and the transitions play a role in paints, inks, cosmetics, pharmaceuticals and food1. There are also dense suspensions such as corn starch which exhibit jamming transitions and, in some cases, could allow you to run on their surface without sinking.
The question is: What happens during these transitions? Liquids brought to the transitional regime display collective (temporarily and spatially synchronized) motion of molecules and particles. Consequently, relaxation times are much longer from those in bulk2,3,4, viscosity increases by many orders of magnitude and, when sheared, confined liquids may experience smooth, stick-slip or chaotic responses5,6,7,8,9. The collective motion triggers dynamic heterogeneities with a supermolecular length ranging from a few up to ten molecular distances10,11,12,13. Heterogeneities of a similar kind are observed in various suspensions14 and, among them, in blood subjected to a transient flow15. We also know that strong stimuli drive viscoelastic liquids to the transitional state. An impact-activated solidification has been observed in dense suspensions16 and an aligned motion of molecules is detected in liquids subjected to shock17.
Molecular dynamics simulations provide excellent insight into the transitional phenomena18,19,20,21. The simulations are followed by thermodynamics-based models22,23 and minimalistic models24,25,26; the latter two are suitable for the replication of the observed behaviors. Also, the transitions are studied in the framework of non-Newtonian fluid dynamics27,28. As we noted earlier, the transitions emerge in over-constrained liquids where molecules lose their ability to move freely and, consequently, are forced to act in a collective manner.
In here, the transitional regime is the regime of our interest.
Our assertion is that a continuum-level approach can be useful in forecasting the transitions so long as the approach is brought close enough to the molecular scale. In our case, this is done by accounting for the relevant spatial and temporal fluctuations known as the dynamic heterogeneities29. Also, we assume that the substance in the liquid-like and solid-like states is different enough for the behaviors to be governed by independent constitutive equations. By comparing the two we derive criteria for the liquid-solid and liquid-liquid transitions in equilibrium and at steady state. The analysis prepares us for a more challenging task, namely the prediction of the LLSTs during transient flow processes. We illustrate the later in the example of blood subjected to an idealized cardiac cycle.
Results
Dynamic heterogeneity
Let's consider a viscoelastic liquid, where the monitored particle moves from its initial position {Xk} to a less than optimal position {xk}, Fig. 1. The “optimal” position refers to the thermodynamically most favorable (mean) positin {zk}. From this point of view, a collective motion of a few atoms in monatomic liquids (transit) can be considered a deviation from the expected trajectory30. In liquids, the current position of a molecule often diverges from the optimal position, but the trajectory must be physically admissible, i.e. it must be consistent with the constraints imposed by the conservation laws. In the framework of continuum, we expect to find the material particle (particle and its surroundings) in an acceptable position determined by the equations of motion  , where the components of the current stress are σij, the particle acceleration is
, where the components of the current stress are σij, the particle acceleration is  and, as usual, mass density is ρ. Any deviation from the thermodynamically optimal trajectory [
and, as usual, mass density is ρ. Any deviation from the thermodynamically optimal trajectory [ versus
versus  ] triggers perturbations in stress. Consider stress tractions plotted on a surface normal to the direction of flow {nk}. The tractions in the optimal and actual positions may not be the same
] triggers perturbations in stress. Consider stress tractions plotted on a surface normal to the direction of flow {nk}. The tractions in the optimal and actual positions may not be the same  and the difference is responsible for stress fluctuations
and the difference is responsible for stress fluctuations

Stress in the reference (optimal) position is  and in the actual position {xk} is σik. Using divergence theorem, the stress perturbations centered about
and in the actual position {xk} is σik. Using divergence theorem, the stress perturbations centered about  become
become  . The material length
. The material length  is understood as the dominant length and it captures the relevant spatial stretch of the stress gradient. Next, the stress gradient is replaced by the inertia term taken from the equations of motion, while volume V0 is reduced to a material point
is understood as the dominant length and it captures the relevant spatial stretch of the stress gradient. Next, the stress gradient is replaced by the inertia term taken from the equations of motion, while volume V0 is reduced to a material point  . As a result, the perturbations are simplified to
. As a result, the perturbations are simplified to  . We assume that the tensor
. We assume that the tensor  is symmetric and, then, we have
is symmetric and, then, we have  . However, the symmetry restriction does not need to be enforced. The stress fluctuations are incorporated into the constitutive description of the liquid and the solid. In the transitional regime, the liquid is prone to shear and may experience changes in mass density. This behavior is described by the Maxwell-like viscoelastic model
. However, the symmetry restriction does not need to be enforced. The stress fluctuations are incorporated into the constitutive description of the liquid and the solid. In the transitional regime, the liquid is prone to shear and may experience changes in mass density. This behavior is described by the Maxwell-like viscoelastic model

where strain rate is  . In this relation, elastic matrix is Cijkl and η is viscosity. Viscosity is determined by averages over a spectrum of relaxation times31. Usually, the viscous term in (2) is based on stress deviator alone. In this case, shear stress and pressure are viscous quantities32,33. Also, the elastic matrix includes contributions of bulk and shear moduli. The last term in (2) captures the contribution of the stress perturbations. The perturbations
. In this relation, elastic matrix is Cijkl and η is viscosity. Viscosity is determined by averages over a spectrum of relaxation times31. Usually, the viscous term in (2) is based on stress deviator alone. In this case, shear stress and pressure are viscous quantities32,33. Also, the elastic matrix includes contributions of bulk and shear moduli. The last term in (2) captures the contribution of the stress perturbations. The perturbations  are added to the mean stress denoted as σij. In the constitutive relation, the parameter
are added to the mean stress denoted as σij. In the constitutive relation, the parameter  resembles the Reynolds number and, for this reason, we call it the material Reynolds number. We introduce the number for reasons discussed later. In here, kinematic viscosity is
resembles the Reynolds number and, for this reason, we call it the material Reynolds number. We introduce the number for reasons discussed later. In here, kinematic viscosity is  and υs is sound velocity. When the tensors
and υs is sound velocity. When the tensors  and
and  are not symmetric, we expect the non-symmetry would trigger perturbations in flow. The rate of mechanical work performed by the material is
are not symmetric, we expect the non-symmetry would trigger perturbations in flow. The rate of mechanical work performed by the material is  . The state function GL and the dissipation potential
. The state function GL and the dissipation potential  are
are  and
and  , respectively. We omit the contribution of heat flux. The flux
, respectively. We omit the contribution of heat flux. The flux  in (2) may become a powerless quantity when the term
in (2) may become a powerless quantity when the term  is equal to zero. As suggested34, the powerless flux captures the contribution of hidden micro-scale dynamic events.
is equal to zero. As suggested34, the powerless flux captures the contribution of hidden micro-scale dynamic events.
The liquid is said to be converted to a viscoelastic solid-like material. In the simplest circumstance, the solid follows the Kelvin-Voigt behavior and includes the contribution of the micro-inertia described in (1), thus

The time span (t − t0) is taken to include the relevant history of the perturbations. This means that the material retains a short memory of the past history but this memory fades away beyond (t − t0)31,35. In here, mechanical work is  . The state function is
. The state function is  and the dissipation potential becomes
and the dissipation potential becomes  . With the use of normality rules36 the dissipation potential captures viscous stress
. With the use of normality rules36 the dissipation potential captures viscous stress  in (3). The contribution of the dynamic heterogeneity
in (3). The contribution of the dynamic heterogeneity  is linked to the relevant change in particle momentum. Under certain conditions the responses produced by the liquid (Eqn. 2) and the solid (Eqn. 3) become indistinguishable. This is what we call the liquid-liquid transitional state (liquid II).
is linked to the relevant change in particle momentum. Under certain conditions the responses produced by the liquid (Eqn. 2) and the solid (Eqn. 3) become indistinguishable. This is what we call the liquid-liquid transitional state (liquid II).
LST- near-equilibrium scenario
We place the liquid (2) into a small container. Walls of the container restrict the motion of molecules and, in this manner, contribute to the increase of viscosity. In equilibrium, the fluctuations represent the primary response of the substance and, therefore, we omit the inertia terms in (2) and (3). In a one-dimensional setting, the nano-scale stress in the position {x} is calculated from the equation of motion  , where σ and σz are stresses in the actual and optimal positions. At a larger (meso) scale, the stress becomes
, where σ and σz are stresses in the actual and optimal positions. At a larger (meso) scale, the stress becomes  . Next, we separate the spatial and temporal terms in velocity
. Next, we separate the spatial and temporal terms in velocity  and substitute the nano- and meso-stresses into the truncated constitutive equations (2) and (3). The nano-scale spatial perturbations
and substitute the nano- and meso-stresses into the truncated constitutive equations (2) and (3). The nano-scale spatial perturbations  in the liquid and the solid are Gaussian
in the liquid and the solid are Gaussian  and, then, become harmonic at meso-scale
and, then, become harmonic at meso-scale  , where
, where  is the magnitude of the perturbations. In the next step, we determine the temporal contribution υt(t). It turns out that the expression for υt(t) is scale independent (regardless whether it is the nano- or meso-scale), but υt(t) is different in the liquid and the solid
is the magnitude of the perturbations. In the next step, we determine the temporal contribution υt(t). It turns out that the expression for υt(t) is scale independent (regardless whether it is the nano- or meso-scale), but υt(t) is different in the liquid and the solid

In here, the characteristic relaxation time is  , while
, while  is sound velocity and, as before,
is sound velocity and, as before,  is kinematic viscosity. The elastic constant is reduced to a single parameter C. A substance in the liquid and the solid state has very different properties and these properties become comparable only within the LST regime. The two expressions in (4) become identical when the material Reynolds number
is kinematic viscosity. The elastic constant is reduced to a single parameter C. A substance in the liquid and the solid state has very different properties and these properties become comparable only within the LST regime. The two expressions in (4) become identical when the material Reynolds number  is equal to one. We conclude that the liquid-solid transition emerges when
is equal to one. We conclude that the liquid-solid transition emerges when

The magnitude of kinematic viscosity increases as the size of the confinement becomes smaller7,8,37,38. As indicated, the transitional length in water, hexadecane, cyclohexane and other substances is in the range of six to ten molecular distances. When knowing sound velocity and viscosity (both measured at small scales), the predicted characteristic length  is within the range observed in the experiments and predicted in molecular dynamics simulations.
is within the range observed in the experiments and predicted in molecular dynamics simulations.
LLT- steady flow
We have shown that spatial nano-fluctuations in equilibrium are Gaussian and become harmonic at meso-scale. It is suggested that steady shear makes the fluctuations non-Gaussian39 and, then, the fluctuations (1) trigger the liquid-liquid transition. We begin by enforcing conservation of mass  and momentum
and momentum  , where the Cauchy stress is σ, velocity is
, where the Cauchy stress is σ, velocity is  and displacement is denoted as u. All the variables are expressed in terms of moving coordinate system
and displacement is denoted as u. All the variables are expressed in terms of moving coordinate system  , where the steady velocity is D. Consequently, we have
, where the steady velocity is D. Consequently, we have  ,
,  and strain is
and strain is  . Stress is derived directly from the conservation laws and is
. Stress is derived directly from the conservation laws and is  . In here, velocity is
. In here, velocity is  and ρ0 is the initial mass density.
and ρ0 is the initial mass density.
As in the near equilibrium scenario, we predict the liquid-solid transition by comparing Eqns. 2 and 3; in here, both the relations include the contributions of the dynamic heterogeneities. The transition occurs when

Note that at  the two material numbers are equal
the two material numbers are equal  and, consequently, the two criteria (5) and (6) become identical. The transitional liquid (liquid II) should exhibit the properties described by (2) and (3). From the solution presented in Methods A, flow patterns exhibited by the liquid II are limited to
and, consequently, the two criteria (5) and (6) become identical. The transitional liquid (liquid II) should exhibit the properties described by (2) and (3). From the solution presented in Methods A, flow patterns exhibited by the liquid II are limited to

where u1 and u2 are constants. From (7) we see that the liquid II cannot be formed at  . In all other situations
. In all other situations , the liquid II must follow the script defined in (7). There are four scenarios:
, the liquid II must follow the script defined in (7). There are four scenarios:
-
1
At
 , the substance is in its solid state (pastes, wet sands and other dense suspensions) exhibiting high resistance to flow (high viscosity). As a result, the material Reynolds number is small
, the substance is in its solid state (pastes, wet sands and other dense suspensions) exhibiting high resistance to flow (high viscosity). As a result, the material Reynolds number is small  . The solid-liquid conversion is accomplished by applying a standing wave designed according to the protocol (7). The most known phenomenon of this kind is soil liquefaction40.
. The solid-liquid conversion is accomplished by applying a standing wave designed according to the protocol (7). The most known phenomenon of this kind is soil liquefaction40. -
2
One may envision another situation, where a viscoelastic liquid
 is subjected to the standing wave. In this manner, the liquid is forced to act as if it were a liquid II substance. Such experiments have been conducted14,41 and show the formation of microstructural patterns. We are interested in predicting the aggregation and disaggregation of red cells in blood not only under the steady state but also during transient flow42.
is subjected to the standing wave. In this manner, the liquid is forced to act as if it were a liquid II substance. Such experiments have been conducted14,41 and show the formation of microstructural patterns. We are interested in predicting the aggregation and disaggregation of red cells in blood not only under the steady state but also during transient flow42. -
3
Exponential flow of liquid II occurs at
 . Strongly driven liquids (under shock or impact) fit well the scenario. Often, it is assumed that shock wave
. Strongly driven liquids (under shock or impact) fit well the scenario. Often, it is assumed that shock wave 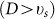 has a sharp shock transition. In reality, the transition consists of several molecular layers of aligned molecules15 which (we predict) are organized within a thin membrane. The membrane travels through the material with shock velocity. Impact loading is also known to trigger the liquid-liquid conversions16.
has a sharp shock transition. In reality, the transition consists of several molecular layers of aligned molecules15 which (we predict) are organized within a thin membrane. The membrane travels through the material with shock velocity. Impact loading is also known to trigger the liquid-liquid conversions16. -
4
We predict that the liquid II behavior may emerge in liquids pushed from equilibrium and, then, allowed to relax according to the rules in (7). Supercooled liquids may fit the scenario, where a controllable decrease of temperature leads to an increase of viscosity, thus, affecting the substance's relaxation time21. We are not aware of any other experimental work done in this area.
LLST- short-lived transitions in blood during cardiac cycle
In simple terms, blood is a liquid tissue consisting of plasma and blood cells. On average 1 microliter of blood contains about  red cells. Thus, in larger vessels (diameter 2 mm or larger), the number of cells is large enough for blood to become a homogeneous viscoelastic liquid. Blood viscosity and elasticity strongly depend on the actual blood composition, flow rate, shape and size of the blood vessels. A steady flow is fastest at the center of the vessel and slowest near the wall. This non-uniformity is linked to the buildup of wall shear stress. A pulsatile cycle produces considerably more complex flow patterns43,44. It is observed that vessel segments with low wall shear stress and oscillatory changes in flow direction appear to be at high risk for the development of various diseases and among them atherosclerosis and thrombosis. Atherosclerosis affects the inner lining of an artery and is characterized by plaque deposits that block the flow of blood. Thrombosis is the formation of clots capable of obstructing the flow of blood. Factors that affect blood viscosity45,46,47,48 are: hematocrit, red cell aggregation and deformation, plasma viscosity, concentration and size of low-density lipoproteins (LDL) and age.
red cells. Thus, in larger vessels (diameter 2 mm or larger), the number of cells is large enough for blood to become a homogeneous viscoelastic liquid. Blood viscosity and elasticity strongly depend on the actual blood composition, flow rate, shape and size of the blood vessels. A steady flow is fastest at the center of the vessel and slowest near the wall. This non-uniformity is linked to the buildup of wall shear stress. A pulsatile cycle produces considerably more complex flow patterns43,44. It is observed that vessel segments with low wall shear stress and oscillatory changes in flow direction appear to be at high risk for the development of various diseases and among them atherosclerosis and thrombosis. Atherosclerosis affects the inner lining of an artery and is characterized by plaque deposits that block the flow of blood. Thrombosis is the formation of clots capable of obstructing the flow of blood. Factors that affect blood viscosity45,46,47,48 are: hematocrit, red cell aggregation and deformation, plasma viscosity, concentration and size of low-density lipoproteins (LDL) and age.
Our objective is to forecast liquid-liquid-solid transitions in blood during cardiac cycle49. In our idealized scenario, the vessel is a rigid tube with inner radius  . The tube is filled with blood and the system stays at rest. The derivations are based on Lagrange description, where strains are small, times are relatively short
. The tube is filled with blood and the system stays at rest. The derivations are based on Lagrange description, where strains are small, times are relatively short  . The tube is large enough for the blood to remain in its liquid state
. The tube is large enough for the blood to remain in its liquid state  . Next, the tube is rapidly moved from rest along its axis and kept in motion at constant velocity
. Next, the tube is rapidly moved from rest along its axis and kept in motion at constant velocity  , Fig. 2. Blood slippages along the walls are not allowed. Whole blood in the state (L) is the viscoelastic liquid (2), where the temporal and spatial fluctuations are considered important. The blood in the transitional state (T) exhibits the properties of both the liquid (L) and the solid (S). The solid-like behavior is described in terms of the “local” Kelvin-Voigt model, where the stress fluctuations are omitted. The liquid (L), liquid II (T) and solid (S) are glued together, Fig. 2. The boundary of the liquid rL with respect to the boundary of the solid rS in the presence of the liquid II
, Fig. 2. Blood slippages along the walls are not allowed. Whole blood in the state (L) is the viscoelastic liquid (2), where the temporal and spatial fluctuations are considered important. The blood in the transitional state (T) exhibits the properties of both the liquid (L) and the solid (S). The solid-like behavior is described in terms of the “local” Kelvin-Voigt model, where the stress fluctuations are omitted. The liquid (L), liquid II (T) and solid (S) are glued together, Fig. 2. The boundary of the liquid rL with respect to the boundary of the solid rS in the presence of the liquid II  must be optimal in terms of the rate of work performed by the system
must be optimal in terms of the rate of work performed by the system  , where the wall shear stress is
, where the wall shear stress is  and
and  is shear stress. Expressions for the particle velocity and stress in each state are presented in Methods B. Blood viscosity and elasticity are determined for whole-blood (hematocrit 38%), where
is shear stress. Expressions for the particle velocity and stress in each state are presented in Methods B. Blood viscosity and elasticity are determined for whole-blood (hematocrit 38%), where  and
and  . In each solution, the radius le of the vessel is equal to the significant stretch lc of the stress gradient. As stated earlier, the vessel is rapidly moved from rest and kept in motion at constant velocity
. In each solution, the radius le of the vessel is equal to the significant stretch lc of the stress gradient. As stated earlier, the vessel is rapidly moved from rest and kept in motion at constant velocity  . In terms of cardiac cycle this is the worst case scenario. The analysis is constructed for relatively large vessels, where the diameter is varying between three to six millimeters. These diameters correspond to the material Reynolds number
. In terms of cardiac cycle this is the worst case scenario. The analysis is constructed for relatively large vessels, where the diameter is varying between three to six millimeters. These diameters correspond to the material Reynolds number  in the range of two to four. Rapid departure from rest converts the liquid (L) into the liquid II (T) and the solid-like material (S), Fig. 2. In all the studied cases, clock is set to zero when all particles across the tube start sensing the motion, while the particle velocity at the center of the tube is still equal to zero. This setup properly replicates the velocity distribution in the tube at the moment of the blood flow reversal49. In the first example
in the range of two to four. Rapid departure from rest converts the liquid (L) into the liquid II (T) and the solid-like material (S), Fig. 2. In all the studied cases, clock is set to zero when all particles across the tube start sensing the motion, while the particle velocity at the center of the tube is still equal to zero. This setup properly replicates the velocity distribution in the tube at the moment of the blood flow reversal49. In the first example , at t = 0 the entire vessel contains blood in the transitional (T) and solid (S) states, Fig. 2. Gradually, blood is converted back to its liquid form (L) and at t ≈ τ0 the conversion is complete, where
, at t = 0 the entire vessel contains blood in the transitional (T) and solid (S) states, Fig. 2. Gradually, blood is converted back to its liquid form (L) and at t ≈ τ0 the conversion is complete, where  . There is a moment when the transitional liquid (T) disappears and a sharp liquid-solid interface emerges
. There is a moment when the transitional liquid (T) disappears and a sharp liquid-solid interface emerges  . At this point, the L-S interface migrates toward the tube walls. Stress tractions along the L-S interface are satisfied but velocity becomes discontinuous causing slippages. Such slippages have been observed in vessels near the vessel walls in a plasma layer of the thickness about 45.8 μm15,49. In larger vessels
. At this point, the L-S interface migrates toward the tube walls. Stress tractions along the L-S interface are satisfied but velocity becomes discontinuous causing slippages. Such slippages have been observed in vessels near the vessel walls in a plasma layer of the thickness about 45.8 μm15,49. In larger vessels  , the layers T and S are smaller and the conversion process is faster (Fig. 3). An indirect support for the LLSTs in blood at transient conditions is offered in ref. 15. The presence of the transitional and solid-like blood near the vessel walls is a concerning factor. We should note that an increase of blood viscosity and/or measurable decrease of elasticity may further aggravate the problem. Often, blood viscosity is considered the unifying indicator of cardiovascular diseases. It seems that the material Reynolds number would be a better predictor of cardiovascular disease risk.
, the layers T and S are smaller and the conversion process is faster (Fig. 3). An indirect support for the LLSTs in blood at transient conditions is offered in ref. 15. The presence of the transitional and solid-like blood near the vessel walls is a concerning factor. We should note that an increase of blood viscosity and/or measurable decrease of elasticity may further aggravate the problem. Often, blood viscosity is considered the unifying indicator of cardiovascular diseases. It seems that the material Reynolds number would be a better predictor of cardiovascular disease risk.
A rigid tube filled with blood is rapidly moved in axial direction (x) at constant velocity.
Initially, the velocity gradient triggers liquid-liquid-solid transitions but, later, blood is converted back to its liquid form. The liquid (L), transitional liquid (T) and solid (S) are marked in the tube and are plotted as a function of time. Velocity distributions are shown in 2-D and 3-D representations and are plotted for t = 0, 50, 100 and 150 ms.
In the upper right corner of the figure, we show the relaxation of the solid (S) and transitional (T) phases as a function of time for three vessels (D = 3.78, 4.54 and 6.04 nm).
The liquid II (T) and the solid (S) phases vanish faster as the size of the vessel increases. Also, the thickness of the T-S layer is plotted as a function of the vessel diameter. At the initial time of the flow reversal (t = 0), the T-S layer has a measurable thickness even in a very large vessel (D ≥ 20 mm). However, the size of the layer shrinks with the progression of time, as shown in instances (t = 10, 20, 30, 40 and 50 ms).
Discussion
There are two aspects of the work worth noticing. First, our continuum level approach is adapted for a small scale analysis. We accomplish this by incorporating the spatial and temporal stress fluctuations into the material's description. Second, we view the substance either as a liquid-like or solid-like material. Thus, we diverge from the approaches where the liquid-like, solid-like and the transitional behaviors are constructed within a single mathematical framework. In this manner, we gain additional degree of freedom which we find necessary when describing the transitional processes. Consequently, we predict LLSTs during active flow processes (steady or transient); where in some circumstances the substance is hard driven. There are several mechanisms by which the transitions occur. Our criterion for the liquid-solid transformation works for liquids in small confinements. We predict microstructural reorganizations in liquids stimulated by standing waves, as we show that the standing waves are responsible for triggering liquefaction in dense suspensions. A synchronized motion of molecules (or particles in suspension) is forecasted in liquids subjected to an impact and/or shock loading. Lastly, we indicate that the liquid-liquid transitions should occur in liquids pushed away from equilibrium and, then, are allowed to relax according to a controllable scenario.
Methods
A. Transitional liquid (liquid II):
Suppose that the liquid-like and solid-like behaviors are indistinguishable. If so, we can substitute stress from (3) into the flow equation (2) and construct a general solution. First, we introduce an effective velocity

Next, we define an effective strain rate

The liquid II obeys the relations (2) and (3). We find that with the use of the new variables (A.1) and (A.2) the transitional liquid must follow the rule defined below

In here,  is the initial velocity and
is the initial velocity and  is the initial strain rate. In addition, the material in the transitional state must adhere to the conservation laws. Under the condition of steady flow
is the initial strain rate. In addition, the material in the transitional state must adhere to the conservation laws. Under the condition of steady flow  , the rules (A3) are
, the rules (A3) are

where stress is  . Solution of the problem is presented in terms of displacements and stresses, namely
. Solution of the problem is presented in terms of displacements and stresses, namely

B. LLST in rigid vessel:
In a rigid vessel filled with blood, velocity and shear stress in the liquid (L) satisfy the equation of motion and are

There are two constants, namely  and
and  . Moreover, the velocity gradient in the center of the tube is always equal to zero
. Moreover, the velocity gradient in the center of the tube is always equal to zero  , where
, where  .
.
The responses of the liquid II are constructed by solving the equation (A.3). Consequently, velocity and shear stress are

The transitional flow is determined in terms of three constants  ,
,  and
and  .
.
Lastly, the solution for the solid is

where  and
and  are constants. Boundary conditions for this problem are defined as follows:
are constants. Boundary conditions for this problem are defined as follows:

We have seven constants  and two time-dependent variables
and two time-dependent variables  . The LLT and LLST boundaries are determined from the criterion of least action
. The LLT and LLST boundaries are determined from the criterion of least action

References
Xia, Y., Gates, B., Yin, Y. & Lu, Y. Monodispersed colloidal spheres: old materials with new applications. Advanced Materials 12, 693–713 (2000).
Hu, H.-W., Carson, G. A. & Granick, S. Relaxation time of confined liquids under shear. Phys. Rev. Lett. 66, 2758–2761 (1991).
Uebler, E. A. Velocity relaxation in viscoelastic liquids. Ind. Eng. Chem. Fundam. 10, 250–254 (1971).
Tsong, T. Y. & Kanehisa, M. I. Relaxation phenomena in aqueous dispersions of synthetic lecithins. Biochemistry, 16, 2674–2680 (1977).
Drummond, C. & Israelachvili, J. Dynamic phase transitions in confined lubricant fluids under shear. Phys. Rev. E 63, 041506(1–11) (2001).
Demirel, A. L. & Granick, S. Friction fluctuations and friction memory in stick-slip motion. Phys. Rev. Lett. 77, 4330–4333 (1996).
Yoshizawa, H. & Israelachvili, J. Fundamental mechanisms of interfacial friction. 2. Stick-slip friction of spherical and chain molecules. J. Phys. Chem. 97, 11300–11313 (1993).
Klein, J. & Kumacheva, E. Simple liquids confined to molecularly thin layers. I. Confinement-induced liquid-to-solid phase transitions. J. Chem. Phys. 108, 6996–7009 (1998).
Drummond, C., Alcantar, N. & Israelachvili, J. Shear alignment of confined hydrocarbon liquid film. Phys. Rev. E 66, 011705 (1–6) (2002).
Kivelson, S. A. & Tarjus, G. In search of a theory of supercooled liquids. Nature 7, 831–833 (2008).
Kob, W., Roldan-Vargas, S. & Berthier, L. Non-monotonic temperature evolution of dynamic correlations in glass-forming liquids. Nature Physics 8, 164–167 (2012).
Murata, K. & Tanaka, H. Liquid-liquid transition without macroscopic phase separation in water-glycerol mixture. Nature Materials 11, 436–443 (2012).
Kurita, R. & Tanaka, H. Critical-like phenomena associated with liquid-liquid transition in a molecular liquid. Science 306, 845–848 (2004).
Vermant, J. & Solomon, M. J. Flow-induced structure in colloidal suspensions. J. Phys.: Condens. Matter 17, R187–R216 (2005).
Hou, J.-X. & Shin, S. Transient microfluidic approach to the investigation of erythrocyte aggregation: Comparison and validation of the method. Korea-Australia Rheology Journal 20, 253–260 (2008).
Waitukaitis, S. R. & Jaeger, H. M. Impact-activated solidification of dense suspensions via dynamic jamming fronts. Nature, 487, 205–209 (2012).
Schlamp, S. & Haltorn, B. C. Molecular alignment in a shock wave. AIP Phys. Fluids 18, 096101 (1–8) (2006).
Thompson, P. A. & Grest, G. S. Phase transitions and universal dynamics in confined films. Phys. Rev. Lett. 68, 3448–3451 (1992).
Kim, W. K. & Falk, M. L. Role of intermediate states in low-velocity friction between amorphous surfaces. Phys. Rev. B 84, 165422 (1–5) (2011).
Harrington, S. et al. Liquid-liquid phase transition: Evidence from simulations. Phys. Rev. Lett. 78, 2409–2412 (1997).
Sastry, A. & Angell, C. A. Liquid-liquid phase transition in supercooled silicon. Nature Materials 2, 739–743 (2003).
Craster, R. V. & Matar, O. K. Dynamics and stability of thin liquid films. Rev. Modern Physics 81, 1131–1198 (2009).
Binder, K. Theory of first-order phase transitions. Rep. Prog. Phys. 50, 783–859 (1987).
Abel, D. G., Krylov, S. Y. & Frenken, J. W. M. Evidence for contact delocalization in atomic scale friction. Phys. Rev. Lett. 99, 166102 (1–4) (2007).
Sang, Y., Dube, M. & Grant, M. Thermal Effects on atomic friction. Phys. Rev. Lett. 87, 17430 (1–4) (2001).
van Spengen, W. M., Turq, V. & Frenken, J. W. M. The description of friction of silicon MEMS with surface roughness: virtues and limitations of a stochastic Prandtl-Tomlinson model and the simulation of vibration-induced friction reduction. Beilstein J. Nanotechnol. 1, 163–171 (2010).
Craster, R. V. Dynamics and stability of thin films. Rev. Modern Phys. 81, 1131–1198 (2009).
Stickel, J. J. & Powell, R. L. Fluid mechanics and rheology of dense suspensions. Annu. Rev. Fluid Mech. 37, 129–149 (2005).
Tanaka, H., Kawasaki, T., Shintani, H. & Watanabe, K. Critical-like behavior of glass-forming liquids. Nature Materials 9, 324–331 (2010).
De Lorenzi-Venneri, G., Chisolm, E. D. & Wallace, D. C. Vibration-transit theory of self-dynamic response in a monatomic liquid. Phys. Rev. E 78, 041205 (1–10) (2008).
Angell, C. A. et al. Relaxation in glassforming liquids and amorphous solids. J. Appl. Phys. 88, 3113–3157 (2000).
Bero, C. A. & Plazek, D. J. Volume-dependent rate processes in an epoxy resin. J. Polymer Science: Part B 29, 39–47 (1991).
Meng, Y. & Simon, S. L. Pressure relaxation of polystyrene and its comparison to the shear response. J. Polymer Science: Part B 45, 3375–3385 (2005).
Ostoja-Starzewski, M. & Zubelewicz, A. Powerless fluxes and forces and change of scale in irreversible thermodynamics. J. Phys. A.: Math Theor. 44, 335002 (1–9) (2011).
Coleman, B. D. Thermodynamics of materials with memory. Archive for Rational Mechanics and Analysis 17, 1–46 (1964).
Ziegler, H. & Wehrli, C. The derivation of constitutive relations from the free energy and the dissipation function. Adv. Appl. Mech. 25, 183–238 (1987).
Antognozzi, M., Humphris, A. D. L. & Miles, M. J. Observation of molecular layering in a confined water film and study of the layers viscoelastic properties. Appl. Phys. Lett. 78, 300–302 (2001).
Granick, S. Motions and relaxations of confined liquids. Science 253, 1374–1379 (1991).
Katayama, Y. & Terauti, R. Brawnian motion of a single particle under shear flow. Eur. J. Phys. 17, 136–140 (1996).
Seed, H. B. & Idriss, I. M. Simplified procedure for evaluating soil liquefaction potential. J. of the Soil Mechanics and Foundation Division 97, 1249–1273 (1971).
Cravotto, G. & Cintas, P. Molecular self-assembly and patterning induced by sound waves. Chem. Soc. Rev. 38, 2684–2697 (2009).
Kuznetsova, L. A., Bazou, D., Edwards, G. O. & Coakley, W. T. Multiple three-dimensional mammalian cell aggregates formed away from solid substrata in ultrasound standing waves. Biotechnol. Prog. 25, 834–841 (2009).
Shaaban, A. M. & Duerinckx, A. J. Wall shear stress and early atherosclerosis: A Review. Am. J. Roentgenology 174, 1657–1665 (2000).
Ku, D. N., Giddens, D. P., Zarins, C. K. & Glagov, S. Pulsatile flow and atherosclerosis between plaque location and low and oscillating shear stress. Arteriosclerosis 5, 293–302 (1985).
Wells, R. E. Jr. & Merrill, E. W. Influence of flow properties of blood upon viscosity-hematocrit relationships. J. Clinical Investigations 41, 15911598 (1962).
Thurston, G. B. Viscoelasticity of human blood. Biophysical Journal 12, 12051217 (1972).
Coppola, L. et al. Blood viscosity and aging. Arch. Gerontology and Geriatrics 31, 35–42 (2000).
Slyper, A., Le, A., Jurva, J. & Gutterman, D. The influence of lipoproteins on whole-blood viscosity at multiple shear rates. Metabolism Clinical and Experimental 54, 764–768 (2005).
Malek, A. M., Alper, S. L. & Izumo, S. Hemodynamic shear stress and its role in atherosclerosis. J. Am. Med. Assoc. 282, 2035–2042 (1999).
Acknowledgements
This project has been performed under the auspices of the US Department of Energy. The Los Alamos National Laboratory is operated by Los Alamos National Security, LLC for the NNSA of the U.S. DOE under Contract No. DE-AC52-06NA25396.
Author information
Authors and Affiliations
Contributions
I declare that I wrote the article and that the work is based on my own studies.
Ethics declarations
Competing interests
The author declares no competing financial interests.
Rights and permissions
This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivs 3.0 Unported License. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-nd/3.0/
About this article
Cite this article
Zubelewicz, A. Liquid-liquid-solid transition in viscoelastic liquids. Sci Rep 3, 1323 (2013). https://doi.org/10.1038/srep01323
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep01323
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.


 , the substance is in its solid state (pastes, wet sands and other dense suspensions) exhibiting high resistance to flow (high viscosity). As a result, the material Reynolds number is small
, the substance is in its solid state (pastes, wet sands and other dense suspensions) exhibiting high resistance to flow (high viscosity). As a result, the material Reynolds number is small  . The solid-liquid conversion is accomplished by applying a standing wave designed according to the protocol (7). The most known phenomenon of this kind is soil liquefaction
. The solid-liquid conversion is accomplished by applying a standing wave designed according to the protocol (7). The most known phenomenon of this kind is soil liquefaction is subjected to the standing wave. In this manner, the liquid is forced to act as if it were a liquid II substance. Such experiments have been conducted
is subjected to the standing wave. In this manner, the liquid is forced to act as if it were a liquid II substance. Such experiments have been conducted . Strongly driven liquids (under shock or impact) fit well the scenario. Often, it is assumed that shock wave
. Strongly driven liquids (under shock or impact) fit well the scenario. Often, it is assumed that shock wave 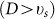 has a sharp shock transition. In reality, the transition consists of several molecular layers of aligned molecules
has a sharp shock transition. In reality, the transition consists of several molecular layers of aligned molecules
