Abstract
We study the influence of noise on information transmission in the form of packages shipped between nodes of hierarchical networks. Numerical simulations are performed for artificial tree networks, scale-free Ravasz-Barabási networks as well for a real network formed by email addresses of former Enron employees. Two types of noise are considered. One is related to packet dynamics and is responsible for a random part of packets paths. The second one originates from random changes in initial network topology. We find that the information transfer can be enhanced by the noise. The system possesses optimal performance when both kinds of noise are tuned to specific values, this corresponds to the Stochastic Resonance phenomenon. There is a non-trivial synergy present for both noisy components. We found also that hierarchical networks built of nodes of various degrees are more efficient in information transfer than trees with a fixed branching factor.
Similar content being viewed by others
Introduction
A challenging research issue is the understanding of the effect of a network topology on the transfer of information1,2,3. Many biological, technical and social systems posses hierarchical structures, e.g., metabolic networks4,5, protein interaction networks6,7,8, the Internet9, theWorld WideWeb10 and social networks11,12,13,14. Topologies of networks evolve over time in order to maximize the systemic efficiency. An important part of this efficiency is the optimal information exchange, even though the meaning and spreading of information varies considerably among such fields as mathematics15, physics16, biology17,18, social science, communication and computer science19,20.
When information is transmitted through a complex network, the process can be represented as an evolution of a distributed information field that is related to the states of network nodes (and/or links) or as paths of localized packages traveling through the network. In the first case, nodes and links can form systems of coupled threshold devices17,19 or oscillators21 that make it possible to propagate a signal from the sender to the receiver. In the second case, the nodes possess some binary variables that can be transmitted from one node to another.
Several authors have considered various features of network typologies that influence information transfers (e.g., if the information flow in a scale-free network is more efficient than in a regular lattice)1,2,3,22. Furthermore, it is shown to be crucial wether a network consists of heterogeneous (e.g. routers and peripheral nodes)1,2 or homogeneous2,3,17,19 nodes with similar connection degrees. Another important attribute is the edge heterogenity in weighted networks23,24 or the network clustering coefficient since a lack of loops in a network can impose a less efficient information transfer25.
There exist several ways to incorporate packet dynamics, from rule simple random walks (e.g.2,26,27,) to more elaborate ways, like biased random walks with some local and/or global navigation rules (e.g.1,3,28,29,30,). It is also possible to implement epidemic models such as SIR (e.g.1,18,31,). Moreover, we can consider single particles (e.g.1,3,26,28,) or interacting particles systems (e.g.2,27,30,). The types of dynamics we choose strongly depends on the interpretation of the modeled information transfer.
This paper considers a prototypical model for the flow of information represented by packages travelling on networks with hierarchical structures. We are particularly interested in the dependency between network structures, noise and information transmission efficiency. We take into account two types of noise in the system. The first one corresponds to a non-deterministic part of system dynamics while the second one to the level of difference between the current network structure in comparison to original one. Numerical simulations show a resonance-like behavior of information transfer efficiency in the presence of both types of noise.
This paper is organized as follows. Section Networks topology and topological noise introduces the topology of hierarchical networks. Section Packet navigation rules describes the imposed packet dynamics. Section Results for artificial networks presents the numerical results for the artificial networks, while Section Real network is devoted to a real hierarchical network based on email exchanges between former Enron employees. Finally, Section Discussion presents the conclusions of our study.
Results
Networks topology and topological noise
This section considers the information flow through hierarchical networks that are organized as a system of communities (e.g.11,12,13,) with an additional feature that we call topological noise. This noise corresponds to the false information that we possess about a network topology and can result, for example, from the process of links rewiring while the data about this process are not stored in an appropriate vector of nodes communities membership. In such a case, a package that is sent from node i to node j can fail to be delivered in a time that is proportional to the network size, since its path is traced using partial error data.
Network with a tree structure
A tree structure can be considered as the most natural hierarchical network model. For simplicity, all nodes in a given tree possesses the same branching factor, n. Therefore the tree is built as follows: there is a single node at the first hierarchical level. The second level consists of n offspring nodes that branch to the third level, which consists of n · n nodes and so on, until it reaches the required level of hierarchy, h, where the tree does not branch further. The branching factor, n and the number of all hierarchy levels, h, are unique tree parameters. At every tree level, 1 < η ≤ h a community is defined as a group of all n nodes at this level with the same “mother-node” at the level η − 1; therefore, there are nη−2 of communities at the level η. The mother node at the level η = 1 will be treated as a separate community. If node, i, belongs to a certain community, it can be described by a vector, ci, of a dimension equal to the total number of all communities  and a lth vector component
and a lth vector component  where the node, i, belongs to the lth community or
where the node, i, belongs to the lth community or  where it does not belong (l = 1, 2, … D). The full information about the network structure can be stored in a network adjacency matrix; however, the community vectors, ci, contain local structure information that will be used in a navigation algorithm for travelling packages (see below).
where it does not belong (l = 1, 2, … D). The full information about the network structure can be stored in a network adjacency matrix; however, the community vectors, ci, contain local structure information that will be used in a navigation algorithm for travelling packages (see below).
Let us assume that the initial tree structure is changed and with a probability, p, every edge is randomly rewired, i.e., a link between nodes i and j can be changed to a link between i and k (here i, j and k are randomly chosen nodes). We assume that the ci vectors of a membership of nodes in communities were defined for a network without noise (p = 0) and are kept constant during topology changes. Therefore, with increasing rewiring probability p it becomes more difficult to receive a packet due to its false community classification. On the other hand, rewiring the links introduces shortcuts and loops to the the original loop-free tree topology that can enhance transmission efficiency. Although the total number of edges is constant for any level of p, we may observe some changes in the node degree distribution P(k), where most important difference occurs at the first hierarchical level. If p → 1, then the original hierarchical structure is completely lost.
Ravasz-Barabási network
Hierarchical networks with a tree topology (without link rewring) posses a zero clustering coefficient, C, this does not reflect the observation of real networks where the coeffficient C ranges from 0:02 to 0:7632. In33, the authors proposed a scale-free network with a high clustering degree, that results from a hierarchical topology. This kind of hierarchical network is very heterogenous, i.e., the nodes degree distribution follows P(k) ∞ k−γ, γ > 0.
We constructed the network in the same iterative way as proposed in33. The first hierarchical level is a community of five fully-connected nodes. The first node is considered a central node and the remaining four nodes are considered peripheral nodes. The second hierarchical level consists of four replicas of the community from the first level. We connect all the peripherial nodes from the second hierarchical level to the central node from the first hierarchical level. Every level of the hierarchical structure is created in the same way, i.e., four replicas of the network thus far constructed are created and the peripheral nodes of this “new” level posess connections to the central node from the first level. In this network, community membership is defined as a group of five fully-connected nodes (all the groups are created as replicas of the first level). This means that we have one community at the first level and four times as many communities at all subsequent levels.
This study takes into consideration a network that consists of three hierarchical levels and N = 125 nodes. In the case of the tree network (See Section Network with a tree structure), we performed a random rewiring process of all existing links with probability, p. However, the information about the rewiring process is not updated in the vectors of the nodes communities membership ci.
Packet navigation rules
We investigate the dynamics of packets displacements on networks. This process represents an information transfer between network nodes. A single package should reach its receiver node in a finite time, T. The navigation rule that governs the packet path possesses a local character and assumes knowledge of the community vectors ci. The deterministic rules are supplemented by a stochastic component that corresponds to the noisy term in the Langevine equation. This means that, with a probability q, the dynamics of the packets are similar to a random walk and with the probability 1 − q, the packet is traveling according to an algorithm that takes into account the community structure. In every time step, the packet moves to one of nearest neighbours of its temporary node. Different packets are considered separately, i.e., no interactions between them are taken into account. The full description of the algorithm for the packet dynamics is as follows:
-
1
First, a sender (s) and a receiver (r ≠ s) nodes are randomly selected for every packet.
-
2
In consecutive time steps, t = 0, …T, the packet travels from node to node. Therefore, packet a arrives at node i in time step t.
-
i
If t < T then the packet navigation algorithm jumps to step (ii). Otherwise, the algorithm loop is completed and the packet is considered undelivered.
-
ii
If in the nearest neighbourhood of node i there is a receiver, r, for packet a then with a probability 1 − q packet a is delivered to its receiver. If not, then the algorithm goes to step (iii).
-
iii
If in the nearest neighbourhood of node i there is a node belonging to the same community as the receiver, r, then with a probability 1 − q, packet, a, is moved to this node. Otherwise, the algorithm moves to step (iv).
-
iv
Packet a is moved to a randomly chosen node from its nearest neighborhood.
-
v
If packet a finds its destination, the loop is completed. If not, then the navigation algorithm returns to the starting point (i).
-
i
All investigated networks are unweighted and undirected. It is important that the algorithm takes into account the membership of nodes in communities as defined in the original network structure (ci vectors), i.e., for the topological noise level p = 0 (before the links are rewired). For p > 0, this leads to false information about the current community structure, i.e. the level of difference between considered network structure in comparison to original one. Particularly in the case of p close to 1 and q ≈ 0, the packet can never reach its destination because of incorrect navigation rules. The case q = 0 is not completely deterministic, i.e., a destination node from one community is chosen randomly from all community members. It is not suprising that in the absence of dynamical noise the algorithm is not optimal. One can imagine some deterministic corrections that can improve efficiency of information transmission. An interesting phenomenon is the influence of both types of noise (q > 0 and p > 0) on each other. The next Section discusses these effects in detail.
In this work we propose a simple model of information transmission that takes advantage of hierarchical community structure of considered networks. More complex rules of packets dynamics and/or different kinds of topologies are possible, e.g. networks without hierarchies but with a visible community structure. For the case of networks when one can not distinguish any cliques algorithms similar to the proposed in this work will be similar to a random walk dynamics. A natural extension of proposed navigation rules could be an algorithm taking into account interactions between packages. In such a case every node would possess a finite capacity thus package arrival times would be important. It would result in a network congestion that would reduce information transfer efficiency. This effect could be avoided if more elaborated rules of packets dynamics are introduced, e.g. a next packet destination is chosen with a probability corresponding to the community membership of packet destination node and the nodes occupation.
Results for artificial networks
We examined the package transmission efficiency for different levels of noise contaminating the network topology, p and the packets' dynamics processes, q. The maximal acceptable time, T, of packet delivery was chosen proportional to the network size T = N. For each pair of parameters, p and q, we consider L = 1,000 packets and the results were averaged over Q = 1,000 realizations, i.e., during the journey of L packets we kept the network topology constant and considered a random ensamble of Q network realizations for every p level. The following quantities were chosen as measures of the system's efficiency:
-
The ratio of delivered packets
 , where Lp describes the number of delivered packets.
, where Lp describes the number of delivered packets. -
The mean inverse of packet delivery time averaged over all packets
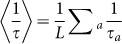 , where τa is the number of time steps after which packet a reached its destination node. If packet a was still undelivered after T time steps, we took
, where τa is the number of time steps after which packet a reached its destination node. If packet a was still undelivered after T time steps, we took 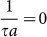 .
.
Figures 1, 2 and 3 represent the results of our simulations.
Information transmission efficiency for tree networks with the presence of a single noise.
In the figures hx ny stands for trees with different number of hierarchies h and different branching factors n, see also main text. (a) Ratio lp(q) of delivered packets as a function of dynamical noise in the absence of topological noise (p = 0). (b) Ratio lp(p) of delivered packets as a function of topological noise in the absence of dynamical noise (q = 0). (c) Averaged inverse time of packet delivery  as a function of dynamical noise, q, in the absence of topological noise (p = 0). (d) Averaged inverse time of packet delivery
as a function of dynamical noise, q, in the absence of topological noise (p = 0). (d) Averaged inverse time of packet delivery  as functions of topological noise, p, in the absence of dynamical noise (q = 0). Sizes of symbols correspond to error bars of standard deviations of mean values over Q realizations.
as functions of topological noise, p, in the absence of dynamical noise (q = 0). Sizes of symbols correspond to error bars of standard deviations of mean values over Q realizations.
Information transmission efficiency for tree networks with the presence of both type of noise.
(a)–(c) Ratio lp(q, p) of delivered packets as a function of both types of noises for trees with different branching factors, n and number of hierarchical levels, h. (d) Averaged inverse time  of packet delivery as a function of both types of noises for n = 16 and h = 3.
of packet delivery as a function of both types of noises for n = 16 and h = 3.
Figure 1 presents the efficiency of packets delivery under the influence of topological or dynamical noise. Trees with various coordination numbers, n and various numbers of hierarchical levels, h, were investigated. As the ratio  describes the tree's slimness (h is the tree's height and n is its width), the three cases can be distinguished:
describes the tree's slimness (h is the tree's height and n is its width), the three cases can be distinguished:  (slim trees),
(slim trees),  (thick trees) and
(thick trees) and  (intermediate trees). Parameters n and h were always chosen in such a way that the total numbers of network nodes, N, were similar for all of the investigated models. More precisely, trees with the following parameters were taken into account: (n = 2, h = 8, N = 255), (n = 6, h = 4, N = 259) and (n = 16, h = 3, N = 273). In Fig. 1(a),(c) the functions lp(q) and
(intermediate trees). Parameters n and h were always chosen in such a way that the total numbers of network nodes, N, were similar for all of the investigated models. More precisely, trees with the following parameters were taken into account: (n = 2, h = 8, N = 255), (n = 6, h = 4, N = 259) and (n = 16, h = 3, N = 273). In Fig. 1(a),(c) the functions lp(q) and  monotonically decreases for all classes of investigated trees. This means that in the absence of topological noise (p = 0) the stochastic component of the system dynamics (q > 0) diminished the efficiency of the packets' delivery, measured both as a fraction lp of delivered packets as well as the mean inverse of the packet delivery time
monotonically decreases for all classes of investigated trees. This means that in the absence of topological noise (p = 0) the stochastic component of the system dynamics (q > 0) diminished the efficiency of the packets' delivery, measured both as a fraction lp of delivered packets as well as the mean inverse of the packet delivery time  . One can also observe that the quantities, lp(q) and
. One can also observe that the quantities, lp(q) and  , are smaller for slimmer trees.
, are smaller for slimmer trees.
On the other hand, the behavior of the system is much more complex when dynamical noice is absent (q = 0) but the topological noise is present (p > 0). The fraction of delivered packets, lp(p), increases for slim trees and is approximately constant for intermediate trees, but decreases for thick trees. This behaviour can be understood as follows: there are two limiting cases when the total number of tree nodes, N, is constant:  (chain) and
(chain) and  (star). It is clear that for the star topology the rewiring of links (p > 0) increases the mean distance 〈x〉 in a network (〈x〉star → 2 when N → ∞); therefore, the fraction of undelivered packets by time T = N increases and the fraction of delivered packets lp decreases. The situation in a chain is quite different. The mean distance is 〈x〉chain → 2N/3 when N → ∞; therefore, it is much larger than a typical range of packet exploration
(star). It is clear that for the star topology the rewiring of links (p > 0) increases the mean distance 〈x〉 in a network (〈x〉star → 2 when N → ∞); therefore, the fraction of undelivered packets by time T = N increases and the fraction of delivered packets lp decreases. The situation in a chain is quite different. The mean distance is 〈x〉chain → 2N/3 when N → ∞; therefore, it is much larger than a typical range of packet exploration  (after N time steps). A random rewiring of links diminishes the mean distance and ultimately, increases the fraction of delivered packets lp(p) (see Fig. 1(b)). However, these arguments are not valid for the behaviour of the mean inverse of the delivery time
(after N time steps). A random rewiring of links diminishes the mean distance and ultimately, increases the fraction of delivered packets lp(p) (see Fig. 1(b)). However, these arguments are not valid for the behaviour of the mean inverse of the delivery time  since this quantity continuously decreases as a function of parameter p (see Fig. 1(d)). The result for a tree with h = 3, n = 16 shows that although the number of undelivered packets increases (Fig. 1(b)) a number of shortcuts that contribute to relatively small delivery times also emerge. The apperance of these shortcuts compensates for the information losses due to undelivered packages in thick trees in the presence of topological noise.
since this quantity continuously decreases as a function of parameter p (see Fig. 1(d)). The result for a tree with h = 3, n = 16 shows that although the number of undelivered packets increases (Fig. 1(b)) a number of shortcuts that contribute to relatively small delivery times also emerge. The apperance of these shortcuts compensates for the information losses due to undelivered packages in thick trees in the presence of topological noise.
These features result in a partial non-trivial behavior of quantities lp and  when both kinds of noise are present (Fig. 2). Since the quantity lp(p) for q = 0 is an increasing function in the case of slim trees
when both kinds of noise are present (Fig. 2). Since the quantity lp(p) for q = 0 is an increasing function in the case of slim trees  this quantity decreases as a function of q for p = 0, thus the maximum of network efficiency observed at Fig. 2(a) for p = 1 and q < 1 is a direct result of Fig. 1(a),(b). For intermediate trees
this quantity decreases as a function of q for p = 0, thus the maximum of network efficiency observed at Fig. 2(a) for p = 1 and q < 1 is a direct result of Fig. 1(a),(b). For intermediate trees  , we observe a similar behaviour, but the maximum shifts towards larger values of q (see Fig. 2(b)). This corresponds to a flat resonance behavior as a function of dynamical noise. On the other hand, for thick trees
, we observe a similar behaviour, but the maximum shifts towards larger values of q (see Fig. 2(b)). This corresponds to a flat resonance behavior as a function of dynamical noise. On the other hand, for thick trees  there were two maxima (see Fig. 2(c)). The first one was for p = 0, q < 0.75 as was expected from Fig. 1(a),(b). The second one is much more pronounced since it emerged in the middle of the two-dimensional p, q parameter domain and possesses clear resonance characteristics. This resonance was not expected from Fig. 1(a),(b) and it was a result of the synergetic interactions between dynamical and topological noises. The effect did not occur for the quantity
there were two maxima (see Fig. 2(c)). The first one was for p = 0, q < 0.75 as was expected from Fig. 1(a),(b). The second one is much more pronounced since it emerged in the middle of the two-dimensional p, q parameter domain and possesses clear resonance characteristics. This resonance was not expected from Fig. 1(a),(b) and it was a result of the synergetic interactions between dynamical and topological noises. The effect did not occur for the quantity  for all three considered types of trees that displayed only a maximum for p ≈ 1 and q ≈ 0, which was anticipated from Figs. 1(c),(d).
for all three considered types of trees that displayed only a maximum for p ≈ 1 and q ≈ 0, which was anticipated from Figs. 1(c),(d).
Fig. 3 demonstrates that the hierarchical Ravasz-Barabási (RB) network (Section Ravasz-Barabási network) possesses a larger information transmission efficiency when compared to the trees. This is probably related to a larger nodes degrees diversity of the network. Moreover, for p = 0 and q < 1, almost all the packages were delivered, i.e., lp(q) ≈ 1 (Fig. 3(a)). When q = 1, the information transfer is still very efficient when compared to the trees (lp(q) > 0.9). Furthermore, in the absence of dynamical noise (q = 0), a large fraction of packets were delivered, but lp(p) decreased with p, i.e. the more random the network topology was the less efficient the information transfer was(Fig. 3(b)). As one can expect, in the absence of topological noise p = 0, the quantity,  , monotonically decreases with q (Fig. 3(a)). In the absence of dynamical noise the quantity lp(p) displays a local maximum for p ≈ 0.25 and monotonically decreases for higher p-values.
, monotonically decreases with q (Fig. 3(a)). In the absence of dynamical noise the quantity lp(p) displays a local maximum for p ≈ 0.25 and monotonically decreases for higher p-values.
The main difference in the information transmission efficiency of the Ravasz-Barabási and tree networks is presented at the Fig. 3(c),(d). We observe that only in the limit of dynamical noise (q = 0) and high level of topological noise (p > 0.7), the information transmission efficiency, as measured by ratio of delivered packets, is not perfect (lp < 1). For all the other cases, almost all of the packages were delivered; therefore, lp ≈ 1 (Fig. 3(c). It is necesssary to stress that the lp quantity is always larger in RB networks than for trees (Figs. 2(a)–(c)). Furthermore,  is always higher for Ravasz-Barabási networks than for the tree networks (packets are delivered faster on heterogenous networks). The optimal range of the delivery parameters are p < 0.5 and q < 0.2 (Fig. 3(d)).
is always higher for Ravasz-Barabási networks than for the tree networks (packets are delivered faster on heterogenous networks). The optimal range of the delivery parameters are p < 0.5 and q < 0.2 (Fig. 3(d)).
Real network
Description of Enron email network
We compared our observations of information transfer efficiency in artificial systems with corresponding parameters of a real network. This study took into account connections between former Enron employees that are available from34. Nodes are email addresses and a link between two nodes means there was at least one email exchange between them (N = 1, 144). The dataset was considered because of its hierarchical structure (see Fig. 4). The communities were identified using the Blondel community detection algorithm35. This is a heuristic method that is based on modularity optimization. Real networks are not perfectly hierarchical and for this reason one can say about an effective value of p, i.e. how many links were rewired and how many links lay outside hierarchy even for p = 0. It is obvious that every community detection algorithm works better when the number of links between communities is smaller. Basing on testing results for the accuracy of well defined nodes community belonging we found the Blondel algorithm beeing appropriate to our case. We detected 22 communities with sizes ranging from 2 to 227. One can say that the Enron email network possesses a heterogenous degree distribution of nodes as well as heterogenous community distribution.
Information transmission efficiency for RB network.
(a) Ratio, lp(q), of delivered packets and averaged inverse time of packet delivery  as functions of dynamical noise, q, in the absence of topological noise (p = 0). (b) Ratio, lp(p), of delivered packets and averaged inverse time of packet delivery
as functions of dynamical noise, q, in the absence of topological noise (p = 0). (b) Ratio, lp(p), of delivered packets and averaged inverse time of packet delivery  as functions of topological noise, p, in the absence of dynamical noise (q = 0). (c) Ratio, lp(q, p), of delivered packets as a function of both types of noises. (d) Averaged inverse time of packet delivery,
as functions of topological noise, p, in the absence of dynamical noise (q = 0). (c) Ratio, lp(q, p), of delivered packets as a function of both types of noises. (d) Averaged inverse time of packet delivery,  , as a function of both types of noises. Sizes of symbols correspond to error bars of standard deviations of mean values over Q realizations.
, as a function of both types of noises. Sizes of symbols correspond to error bars of standard deviations of mean values over Q realizations.
Results for packets dynamics on the Enron email network
We analyze the information transfer efficiency of our packets shipping algorithm in the context of Enron's network topology. As in the case of the trees and the Ravasz-Barabási network (Sec.), we observed the dynamics of L = 1, 000 packets traveling during a maximum T = N time steps and we averaged the results over Q = 1, 000 copies of a network with rewired links. The outcome of numerical simulations is shown in Fig. 5.
As in the case of the artificial networks studied in Sec. we began by the influence of both types of noise separately. In Fig. 5(a) we observe a result similar to that of Section Results for artificial networks, i.e., a monotonic decrease of  while the dynamical noise q increases. This means that the noise dynamics has a negative influence on the transmission efficiency when it is measured by the packet delivery times. However, we stress the fact that the same noisy component also influences the fraction of delivered packets, lp(q) (Fig. 5(a)). In fact, this quantity increases from 0.5 when q = 0 to 0.9 when q ≈ 0.5 (the dynamical noise increases the information transfer by a factor close to 2!) and it stays close to the maximum value until the noise level reaches the value q = 0.75. Such a surprising behaviour was not observed in any of the artifical network studied in Section Results for artificial networks and we attribute this to the strong heterogenity of the distribution of the communities in the Enron network. Our shipping algorithm used a local rule that forwards a packet to any node belonging to a community containing the destination node. Therefore, for large communities (227 connection were detected in the Enron network), a packet spends a great deal of time randomly exploring the community's nodes. It seems that this process is less efficient when compared to a random search of other paths to the community that may be closer to the destination node.
while the dynamical noise q increases. This means that the noise dynamics has a negative influence on the transmission efficiency when it is measured by the packet delivery times. However, we stress the fact that the same noisy component also influences the fraction of delivered packets, lp(q) (Fig. 5(a)). In fact, this quantity increases from 0.5 when q = 0 to 0.9 when q ≈ 0.5 (the dynamical noise increases the information transfer by a factor close to 2!) and it stays close to the maximum value until the noise level reaches the value q = 0.75. Such a surprising behaviour was not observed in any of the artifical network studied in Section Results for artificial networks and we attribute this to the strong heterogenity of the distribution of the communities in the Enron network. Our shipping algorithm used a local rule that forwards a packet to any node belonging to a community containing the destination node. Therefore, for large communities (227 connection were detected in the Enron network), a packet spends a great deal of time randomly exploring the community's nodes. It seems that this process is less efficient when compared to a random search of other paths to the community that may be closer to the destination node.
In the absence of dynamical noise (Fig. 5(b)), one can see a maximum of  for p ≈ 0.15. Above this value, the delivery time of the packets increases. This effect is very similar to the one observed in the Barabasi-Ravasz network (Fig. 3(b)). Figure 5(b) also shows the ratio of delivered packets, lp, as a decreasing function of topological noise, p. When we take into account both types of noise (Fig. 5(c)), the ratio lp(p, q) of the delivered packets peaks at the non-zero values of the parameters p and q. This behavior is only similar to the synergetic effect of the two noises observed for the thick trees presented in Fig. 3(c). In fact, in the case of the Enron network the optimal values of p and q corresponding to the maximal system performance, can be predicted directly from Figs. 5(a) and (b). Figure 5(d) shows that the packages can reach their destination nodes faster in the absence of topological and dynamic noise. This effect was also observed in the Ravasz-Barabási network (Fig. 3(d)).
for p ≈ 0.15. Above this value, the delivery time of the packets increases. This effect is very similar to the one observed in the Barabasi-Ravasz network (Fig. 3(b)). Figure 5(b) also shows the ratio of delivered packets, lp, as a decreasing function of topological noise, p. When we take into account both types of noise (Fig. 5(c)), the ratio lp(p, q) of the delivered packets peaks at the non-zero values of the parameters p and q. This behavior is only similar to the synergetic effect of the two noises observed for the thick trees presented in Fig. 3(c). In fact, in the case of the Enron network the optimal values of p and q corresponding to the maximal system performance, can be predicted directly from Figs. 5(a) and (b). Figure 5(d) shows that the packages can reach their destination nodes faster in the absence of topological and dynamic noise. This effect was also observed in the Ravasz-Barabási network (Fig. 3(d)).
Discussion
A naive understanding of the effect of noise on information transmission is that stochastic components decrease the quality of information processing in the system. On the contrary this study demonstrates that generic packet-delivery undertaken by a local navigation rule in a complex network can benefit from the presence of a topological noise (random rewiring of links) and/or a dynamic noise component (erratic jumps between neighboring nodes). This constructive effect of noise possesses similar features to Stochastic Resonance36,37,38,39,40,41,42,43,44,45, which is common in several physical, biological and technical systems where noise enhances the information transfer efficiency. To quantify this effect in most cases authors calculate SNR, i.e. signal-to-noise ratio which shows system behavior with reference to the noise background. The existence of SNR maximum for a nonzero noise intensity is interpreted as SR. In our system we calculate the ratio of delivered packets, which can be considered as equivalent to SNR. In fact our system is not driven by an external signal however sending packages corresponds to an external influence. In such a way the observed effect of packets delivery improvement (due to nonzero noisy component) resembles SR. We need to add that Stochastic Reosonance in hierarchical networks where nodes are threshold elements was observed in45.
It is also important to note that information transmission is generally more efficient for hierarchicial networks with heterogeneous nodes (i.e., the Ravasz-Barabási network and the Enron email network), than for homogenous structures, e.g., trees with a fixed branching factor, n. In the absence of dynamical noise, q, the mean delivery time increases with p, in the case of trees. However, for the other two considered networks we observed a maximum of  for the intermediate level of the topological noise. For the ratio of delivered packets, the tree behaviour depends on its slimness parameter, i.e.,
for the intermediate level of the topological noise. For the ratio of delivered packets, the tree behaviour depends on its slimness parameter, i.e.,  , where h is the number of hierarchical levels. In the absence of noise in system dynamics (q = 0) where some links are rewired (p > 0), we identify three different cases (Fig. 1(b)). For intermediate trees i.e.,
, where h is the number of hierarchical levels. In the absence of noise in system dynamics (q = 0) where some links are rewired (p > 0), we identify three different cases (Fig. 1(b)). For intermediate trees i.e.,  , number of delivered packets is approximately constant. When the tree is slim, i.e.,
, number of delivered packets is approximately constant. When the tree is slim, i.e.,  , the more links are randomly rewired, the larger the fraction of delivered packets lp(p). This information transfer improvement can be understood as the result of loops that emerge in the rewired system. In fact, the presence of such loops can enhance the network navigation quality since they accelerate the system dynamics, i.e., the vertex discovery rate and the mean topological displacement of a random walker from the origin25. It seems that in the case of slim trees, this effect outperforms the errors that result from false information about the community memberships stored in the community vector. When the tree is thick, i.e.,
, the more links are randomly rewired, the larger the fraction of delivered packets lp(p). This information transfer improvement can be understood as the result of loops that emerge in the rewired system. In fact, the presence of such loops can enhance the network navigation quality since they accelerate the system dynamics, i.e., the vertex discovery rate and the mean topological displacement of a random walker from the origin25. It seems that in the case of slim trees, this effect outperforms the errors that result from false information about the community memberships stored in the community vector. When the tree is thick, i.e.,  , the fraction lp(p) monotonically decreases with p; therefore, the effect of emerging loops is not important for such systems.
, the fraction lp(p) monotonically decreases with p; therefore, the effect of emerging loops is not important for such systems.
It is worth noting that the combination of both noise components results in non-trivial dynamics. In the case of thick trees, the optimal solution for the packet-delivery algorithm (when the lp quality measure is considered) is to have intermediate levels of both types of noise, although the presence of each stochastic contribution decreases the system's efficiency. For the Enron network topology (Fig. 6(c)) the optimal information transfer was observed for non-zero values of parameter q and p < 0.25; however, in this case, it resulted from a resonant character of a single noise influence on the fraction of delivered packages lp (Fig. 6(a),(b)). The most efficient network is the hierarchical Ravasz-Barabási network where the number of delivered packets is always higher than 90% for all the p and q values. Therefore, we conclude that there is a constructive influence of the two types of noise in these systems. In other words, a randomized packet delivery helps to avoid paths from the false topological information.
Information transmission efficiency for the Enron email network.
(a) Ratio, lp(q), of delivered packets and averaged inverse time of packet delivery  as a function of dynamical noise, q, in the absence of topological noise (p = 0). (b) Ratio, lp(p), of delivered packets and averaged inverse time of packet delivery
as a function of dynamical noise, q, in the absence of topological noise (p = 0). (b) Ratio, lp(p), of delivered packets and averaged inverse time of packet delivery  as a function of topological noise, p, in the absence of dynamical noise (q = 0). (c) Ratio, lp(q, p), of delivered packets as a function of both types of noises. (d) Averaged inverse time,
as a function of topological noise, p, in the absence of dynamical noise (q = 0). (c) Ratio, lp(q, p), of delivered packets as a function of both types of noises. (d) Averaged inverse time,  , of packet delivery as a function of both types of noises. Sizes of symbols correspond to error bars of standard deviations of mean values over Q realizations.
, of packet delivery as a function of both types of noises. Sizes of symbols correspond to error bars of standard deviations of mean values over Q realizations.
References
Nekovee, M., Moreno, Y., Bianconi, G. & Marsili, M. Theory of rumour spreading in complex social networks. Physica A 374, 457–470 (2007).
Germano, R. & de Moura, A. P. S. Traffic of particles in complex networks. Phys. Rev. E 74, 036117 (2006).
Danon, L., Arenas, A. & Diaz-Guilera, A. Impact of community structure on information transfer. Phys. Rev. E 77, 036103 (2008).
Jeong, H., Tombor, B., Albert, R., Oltvai, Z. & Barabasi, A.-L. The large-scale organization of metabolic networks. Nature (London) 407, 651 (2000).
Wagner, A. & Fell, D. A. The small world inside large metabolic networks. Proc. R. Soc. London Ser. B 268, 1803 (2001).
Jeong, H., Mason, S., Barabasi, A.-L. & Oltvai, Z. N. Lethality and centrality in protein networks. Nature (London) 411, 41 (2001).
Wagner, A. The Yeast Protein Interaction Network Evolves Rapidly and Contains Few Redundant Duplicate Genes. Mol. Biol. Evol. 18, 1283–1292 (2001).
van Dijk, D., Ertaylan, G., Boucher, C. A. B. & Sloot, P. M. A. Identifying potential survival strategies of HIV-1 through virus-host protein interaction networks. BMC Systems Biology 4, 1 (2010).
Faloutsos, M., Faloutsos, P. & Faloutsos, C. On power-law relationships of the Internet topology. Comput. Commun. Rev. 29, 251 (1999).
Albert, R., Jeong, H. & Barabasi, A.-L. Diameter of the World-Wide Web. Nature (London) 401, 130 (1999).
Newman, M. E. J. The structure of scientific collaboration networks. Proc. Natl. Acad. Sci. U.S.A. 98, 404 (2001).
Newman, M. E. J. Scientific collaboration networks. I. Network construction and fundamental results. Phys. Rev. E 64, 016131 (2001).
Barabasi, A.-L., Jeong, H., Neda, Z., Ravasz, E., Schubert, A. & Vicsek, T. Evolution of the social network of scientific collaborations. Physica A 311, 590 (2002).
Mei, S., Quax, R., van de Vijver, D. A. M. C., Zhu, Y. & Sloot, P. M. A. Increasing risk behaviour can outweigh the benefits of antiretroviral drug treatment on the HIV incidence among men-having-sex-with-men in Amsterdam. BMC Infectious Diseases 11, 118 (2011).
Cover, T. M. & Thomas, J. A. Elements of Information Theory, Willey 2nd edition, (2006).
Karnani, M., Paakkonen, K. & Annila, A. The physical character of information. Proc. R. Soc. A 465, 2155–2175 (2009).
Mino, H. & Durand, D. M. Enhancement of information transmission of sub-threshold signals applied to distal positions of dendritic trees in hippocampal CA1 neuron models with stochastic resonance. Biol. Cybern. 103, 227–236 (2010).
Voelk, B. & Noe, R. Simulation of information propagation in real-life primate networks: longevity, fecundity, fidelity. Behav. Ecol. Sociobiol. 64, 1449–1459 (2010).
McDonnell, M. D., Abbott, D. & Pearce, Ch, E. M. An analysis of noise enhanced information transmission in an array of comparators. Microelectronics Journal 33, 1079–1089 (2002).
Sloot, P. M. A. & Quax, R. Information processing as a paradigm to model and simulate complex systems. Journal of Computational Science pp. 247–249. 9 2012. ISSN: 1877-7503. (DOI: 10.1016/j.jocs.2012.07.001) (2012).
Barbay, S., Giacomelli, G. & Marin, F. Noise-assisted transmission of binary information: Theory and experiment. Phys. Rev. E 63, 051110 (2001).
Lungarella, M., Pitti, A. & Kuniyoshi, Y. Information transfer at multiple scales. Phys. Rev. E 76, 056117 (2007).
Arenas, A., Diaz-Guilera, A. & Guimera, R. Communication in Networks with Hierarchical Branching. Phys. Rev. Lett. 86, 3196 (2001).
Baronchelli, A. & Pastor-Satorras, R. Mean-field diffusive dynamics on weighted networks. Phys. Rev. E 82, 011111 (2010).
Baronchelli, A., Catanzaro, M. & Pastor-Satorras, R. Random walks on complex trees. Phys. Rev. E 78, 011114 (2008).
Duch, J. & Arenas, A. Scaling of Fluctuations in Traffic on Complex Networks. Phys. Rev. Lett. 96, 218702 (2006).
Lizana, L., Rosvall, M. & Sneppen, K. Time Walkers and Spatial Dynamics of Aging Information. Phys. Rev. Lett. 104, 040603 (2010).
Estrada, E. Information mobility in complex networks. Phys. Rev. E 80, 026104 (2009).
Sinatra, R., Gomez-Gardenes, J., Lambiotte, R., Nicosia, V. & Latora, V. Maximal-entropy random walks in complex networks with limited information. Phys. Rev. E 83, 030103(R) (2011).
Wang, W. X., Wang, B. H., Yin, Ch, Y. Xie, Y. B. & Zhou, T. Traffic dynamics based on local routing protocol on a scale-free network. Phys. Rev. E 73, 026111 (2006).
Sloot, P. M. A., Ivanov, S. V., Boukhanovsky, A. V., van de Vijver, D. A. M. C. & Boucher, C. A. B. Stochastic simulation of HIV population dynamics through complex network modeling. International Journal of Computer Mathematics 85, 8 pp. 1175–1187 (2008).
Dorogovtsev, S. N., Goltsev, A. V. & Mendes, J. F. F. Critical phenomena in complex networks. Rev. Mod. Phys. 80, 1275 (2008).
Ravasz, E. & Barabasi, A.-L. Hierarchical organization in complex networks. Phys. Rev. E 67, 026112 (2003).
http://www.cs.cmu.edu/~enron/ accessed: 12 december 2012.
Blondel, V. D. et al. Fast unfolding of communities in large networks. J. Stat. Mech. P10008 (2008).
Gammaitoni, L., Hänggi, P., Jung, P. & Marchesoni, P. Stochastic resonance. Rev. Mod. Phys. 70, 223 (1998).
Benzi, R., Sutera, A. & Vulpiani, A. The mechanism of stochastic resonance. J. Phys. A 14, L453 (1981).
Wiesenfeld, K., Pierson, D., Pantazelou, E., Dames, Ch. & Moss, F. Stochastic resonance on a circle. Phys. Rev. Lett. 72, 2125 (1994).
Vemuri, G. & Roy, R. Stochastic resonance in a bistable ring laser. Physical Review A 39, 4668 (1989).
Fuliński, A. Active Transport in Biological Membranes and Stochastic Resonances. Phys. Rev. Lett. 79, 4926 (1997).
Anishchenko, V. S., Safonova, M. A. & Chua, L. O. Stochastic resonance in Chuaďż′′s circuit driven by amplitude or frequency modulated signals. Int. J. Bifurcation Chaos Appl. Sci. Eng. 4, 441 (1994).
Krawiecki, A. & Hołyst, J. A. Stochastic resonance as a model for financial market crashes and bubbles. Physica A 317, 597–608 (2003).
Matyjaśkiewicz, S., Krawiecki, A., Hołyst, J. A. & Schimansky-Geier, L. Stochastic multiresonance due to interplay between noise and fractals. Phys. Rev. E 68, 016216 (2003).
Krawiecki, A., Matyjaśkiewicz, S., Kacperski, K. & Hołyst, J. A. Noise free stochastic multiresonance near chaotic crises. Phys. Rev. E 64, 041104 (2001).
Kaim, M., Krawiecki, A. Structural stochastic multiresonance in a hierarchical network of coupled threshold elements. Phys. Lett. A 374,4814–4817 (2010).
Acknowledgements
The work was supported by FP7 FET Open project Dynamically Changing Complex Networks-DynaNets EU Grant Agreement Number 233847, European COST Action MP0801 Physics of Competition and Conflicts and Polish Ministry of Science Grant 1029/7.PR UE/2009/7 and Grant 578/N-COST/2009/0. PS acknowledges the Complexity Program at NTU Singapore. The Research was also partly sponsored by a grant from the “Leading Scientist Programd” of the Government of the Russian Federation, under contract 11.G34.31.0019. PS also acknowledges the support from the FET-Proactive grant TOPDRIM, number FP7-ICT-318121.
Author information
Authors and Affiliations
Contributions
A.C.Z., J.H. & P.S. conceived, designed and developed the model. A.C.Z. performed the computer simulations. All authors participated in analyzing the results and the writing of the manuscript.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Rights and permissions
This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivs 3.0 Unported License. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-nd/3.0/
About this article
Cite this article
Czaplicka, A., Holyst, J. & Sloot, P. Noise enhances information transfer in hierarchical networks. Sci Rep 3, 1223 (2013). https://doi.org/10.1038/srep01223
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep01223
This article is cited by
-
Fast and accurate detection of spread source in large complex networks
Scientific Reports (2018)
-
The Over-Extended Mind? Pink Noise and the Ethics of Interaction-Dominant Systems
NanoEthics (2018)
-
Statistical properties of random clique networks
Frontiers of Physics (2017)
-
Capacity of very noisy communication channels based on Fisher information
Scientific Reports (2016)
-
Disorder and dephasing as control knobs for light transport in optical fiber cavity networks
Scientific Reports (2016)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.



 , where Lp describes the number of delivered packets.
, where Lp describes the number of delivered packets. 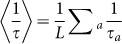 , where τa is the number of time steps after which packet a reached its destination node. If packet a was still undelivered after T time steps, we took
, where τa is the number of time steps after which packet a reached its destination node. If packet a was still undelivered after T time steps, we took 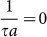 .
. 




