Abstract
We present an approach for genome-wide association analysis with improved power on the Wellcome Trust data consisting of seven common phenotypes and shared controls. We achieved improved power by expanding the control set to include other disease cohorts, multiple races and closely related individuals. Within this setting, we conducted exhaustive univariate and epistatic interaction association analyses. Use of the expanded control set identified more known associations with Crohn's disease and potential new biology, including several plausible epistatic interactions in several diseases. Our work suggests that carefully combining data from large repositories could reveal many new biological insights through increased power. As a community resource, all results have been made available through an interactive web server.
Similar content being viewed by others
Introduction
Most genome-wide association studies consider associations between single-nucleotide polymorphisms (SNPs) and phenotype, one SNP at a time. Increasingly, however, studies are going beyond such low-hanging fruit to richer hypotheses, so as to better understand the causes of complex disease traits. For example, considering pairwise epistatic effects has yielded promising results1,2,3,4. One challenge with exhaustive pairwise analyses is the tremendous amount of statistical power needed to identify associations that can survive the multiple-testing correction. In the Wellcome Trust Case Control Consortium (WTCCC) data5, for example, there are over 60 billion pairs of SNPs that can be tested for association, requiring a P value of less than 8 × 10−13 for significance under Bonferroni correction. One way to address the multiple-testing issue is by way of a two-stage approach, wherein SNP pair hypotheses are pre-filtered with prior knowledge in the first stage and only the remaining pairs are tested in the second stage6. Although such filtering approaches incur a reduced burden from multiple testing, they are susceptible to missing true causal tests by virtue of their inherently imperfect filtering. In this article, we describe an alternative approach that, rather than reducing the number of tests, increases statistical power by making more efficient use of the available data. We developed this approach while looking for epistatic effects in the WTCCC data and present our results on this data, making them fully available as an on-line public resource.
Our strategy for increasing power, while relatively simple in concept, required state-of-the-art analysis techniques and computational resources to implement. Previous epistatic analyses of WTCCC excluded a large number of useable data. Specifically, the other studies discarded (1) individuals from disease cohorts other than the one being studied and (2) non-Caucasian individuals and closely related individuals. We now explain why previous studies did not use these individuals and how our approach enabled us to include them.
To understand the first exclusion of individuals in the standard analysis, note that the WTCCC data consists of genome-wide SNPs and phenotypes for seven common diseases: bipolar disorder (BD), coronary artery disease (CAD), hypertension (HT), Crohn's disease (CD), rheumatoid arthritis (RA), type-I diabetes (T1D) and type-II diabetes (T2D). The WTCCC took great care to consistently use the same data pipeline so as to enable sharing of a common control set for all phenotypes, one of the main contributions of the initial study5. The standard analysis of these data considers each disease phenotype separately. That is, when analyzing a given disease, individuals with that disease (the cases) are always compared with a single, fixed, set of control individuals. In contrast, for a given phenotype, we increase the size of the control set by including all other phenotype cohorts. When expanding the controls in this way, pleiotropy could lead to decreased power. In particular, if a SNP were associated with the disease corresponding to the cases and also with one of the diseases in the expanded controls (with an effect in the same direction), then the resulting association strength would be attenuated. We call this effect negative crosstalk. Expanding the controls could also lead to spurious associations. Specifically, when analyzing a particular phenotype, one could find association signal arising from any of the other diseases only because these are now embedded in the expanded control set, an effect we call positive crosstalk. Although both negative and positive cross-talk are undesirable, there are straightforward procedures for detecting and eliminating them. For example, to mitigate the effects of positive crosstalk, one can look at hypotheses that appear to be pleiotropic in the standard series of analyses and remove all but the most significant from consideration in the expanded analysis. To mitigate the effects of negative crosstalk and inappropriate removal due to positive crosstalk, one could additionally run the analysis on the non-expanded control set.
The second exclusion of non-Caucasian and closely-related individuals is done to avoid confounding by population structure and family relatedness, respectively. The exclusion of these individuals enables the use of simple, fast statistical methods such as linear or logistic regression for the identification of associations. To properly analyze data containing population structure and family relatedness, one could use a linear mixed model (LMM)7,8—a model so computationally expensive that, up until our recent work, it could not be deployed on large data sets9,10,11. Now that our LMMs have the same computational complexity as linear regression, however, we are able to include the formerly excluded individuals and increase power.
Results
We first investigated the improved power offered by our approach on the analysis of univariate associations in the WTCCC data for Crohn's disease because there is a bronze standard (a large meta-analysis) with which to evaluate such results12. We assessed our approach by counting false positives and true positives on a locus-by-locus basis. A standard analysis (i.e., with both exclusions in place and using linear regression) yielded 0 false positive loci and 6 true positive loci. Expanding the control set to include individuals in the remaining six diseases (but still excluding non-Caucasians and closely related individuals) yielded 2 false positive and 13 true positive loci. These false positives did not correspond to significant loci in any of the other six diseases (see Supplementary Dataset 1 ), suggesting that positive crosstalk was not responsible. We therefore posited that the false positives were due to confounders in the expanded control set without the use of a method to correct for them. To test this hypothesis, we applied a LMM on this same data set to correct for them. In doing so, we obtained 1 false positive locus (one less than without the LMM) and (again) 13 true positive loci, suggesting that the LMM did in fact correct for confounding. Finally, removing the second exclusion (i.e., additionally including non-Caucasians and close family members) resulted in 0 false positives and 13 true positives.
In summary, we went from a standard analysis with 6 true positives (and 0 false positives) to our expanded analysis with 13 true positives (and 0 false positives). Significant univariate associations for Crohn's disease and the remaining six phenotypes are given in Supplementary Dataset 2 . Although we found evidence of positive crosstalk within these univariate analyses (see Supplementary Dataset 2 ), as we shall see, we did not see such evidence for epistatic interactions.
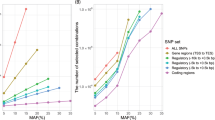
Given the improvement we saw on univariate associations for Crohn's disease, we next applied our expanded approach to the analysis of epistatic interactions for all seven phenotypes ( Supplementary Dataset 3 ). We observed significant (P < 7.9 × 10−13) epistatic interactions for all but the CD phenotype, with no substantial inflation or deflation of P values ( Supplementary Figure 1 ). As noted by Wan et al.1, apparent epistatic interactions for SNP pairs that are too close (within 1 Mb) to each other are potentially false positives due to linkage. Consequently, we removed such associations from further consideration, leaving only those that were well separated. After this proximity filter, epistatic interactions remained for each of the six phenotypes (see Table 1 ). Furthermore, none of these associations were found to have possible positive crosstalk, thus mitigating concerns about this issue. Note that almost all RA epistatic interactions were in the MHC class II region, but that none of these were well separated. In contrast, many T1D epistatic interactions were well separated and showed interactions between MHC class I (29.8 Mb–31.6 Mb) and class II (32.3 Mb–33.4 Mb) as well as interactions between MHC class III (31.6 Mb–32.3 Mb) and class II ( Figure 1 ), which may have clinical significance as discussed in Wan et al.1.
T1D epistatic interactions in the MHC region.
Each point corresponds to a significant, well separated, epistatic interaction in the extended MHC region. Positions of the two SNPs are shown on the x and y axes. Regions on the x-axis corresponding to MHC class I and class III are shaded. All positions shown on the y-axis fall in MHC class II region.
A standard approach for avoiding the onerous computations needed for an exhaustive epistatic analysis is to first exclude SNPs having single-SNP associations with a P value greater than some threshold and then testing only SNP pairs for those SNPs not excluded13. Our exhaustive analysis provides an opportunity to evaluate such an approach. In particular, had we used this approach with the rather liberal P value threshold of 10−6, we would have missed all of the significant epistatic interactions for five of the phenotypes (BD, CAD, HT, RA and TD2) ( Table 1 ).
Overall, the results discussed so far are generally consistent with those of Wan et al.1 who performed an exhaustive search for epistatic interactions on the standard WTCCC data. One difference in results between their analysis and ours is that we did not find the one epistatic interaction in the CD phenotype previously found, which has so far not had any biological support. Another difference is that our analysis found one epistatic interaction in the bipolar disorder phenotype not previously found—in particular, between SNP rs7496665 (on chromosome 15) and SNP rs6142704 (on chromosome 20), the latter of which is in gene CDH4 and thought to play an important role in brain segmentation and neuronal outgrowth.
The most conspicuous difference between our results and those of Wan et al.1 was that we found 42 epistatic interactions for the CAD phenotype ( Supplementary Dataset 2 ), whereas they found none. Among these epistatic interactions, 12 had both SNPs within the same gene, significantly more than one would find due to chance (P = 0.018). Two SNPs are of particular interest because they appeared in many epistatic interactions. The first, rs3798343, appeared in six of the epistatic interactions and is within gene PPARD, previously linked to CAD14. The second, rs17146094, appeared in 15 of the interactions and is within 100 Kb of gene LIMK1, which has also been previously linked to CAD15. Furthermore, these two apparent “hub” SNPs interact strongly with each other (P = 9.4 × 10−18). Finally, we note that Wan et al.1, used a different statistical test for epistasis (see Methods) which may account for some of the differences, although most differences came from our use of the expanded data ( Supplementary Dataset 4 ).
Finally, the genomic-control factor λ16,17 indicated apparent inflation for the univariate tests, with λ ranging from 1.06 to 1.18 across the seven phenotypes. In contrast, the tests for epistatic interactions showed no inflation, with values of λ all less than 1.01 ( Supplementary Figure 1 ). There is a growing consensus that apparent univariate inflation is actually the result of a large number of small polygenic effects on the phenotype18, rather than due to uncontrolled confounders. The near 1.0 values of λ suggest that epistatic effects are not as frequent as univariate ones.
Although we have provided the list of all epistatic interactions found to be significant ( Supplementary Dataset 3 ), researchers interested in particular SNP-SNP or gene-gene interactions may wish to access association P values below our threshold. We provide such access (and access to all univariate associations) by way of an online tool at http://research.microsoft.com/en-us/um/redmond/projects/MSCompBio/.
Discussion
Using data from the Wellcome Trust, we have demonstrated that statistical power can be substantially improved by expanding the control set. This type of expansion should be possible for datasets in large repositories including dbGap. For example, one could combine SNP data obtained from the same platform, although further care would have be taken than in the WTCCC context to ensure that batch effects from sample collection, preparation and analysis were adequately addressed. Procedures similar to the ones described here are likely to help in this regard, although this approach remains an open area of investigation.
Methods
We used data from the Wellcome Trust Case Control Consortium (WTCCC) with their permission. The data consisted of the SNP and phenotype data for seven common diseases: bipolar disorder (BP), coronary artery disease (CAD), Crohn's disease (CD), hypertension (HT), rheumatoid arthritis (RA), type-I diabetes (T1D) and type-II diabetes (T2D). Each phenotype group contained about 1,900 individuals. In addition, the data included a set of approximately 1,500 controls from the UK Blood Service Control Group (NBS). The data did not include a second control group from the 1958 British Birth Cohort (58C), as permissions for it precluded use by commercial organizations.
Note that additional quality control is warranted when testing for epistatic interactions due sparse counts in contingency tables19. Although our expansion of the data somewhat mitigates this need, we did impose stricter quality control. In particular, in addition to the filters described by the WTCCC5, we excluded a SNP if either its minor-allele frequency was less than 1%, or it was missing in greater than 1% of individuals (in both cases on the fully expanded data). Also, because genetic distances were required by FaST-LMM to avoid proximal contamination9,10, we excluded SNPs whose genetic distance were unknown. After filtering, 356,441 SNPs remained. In total, there were 14,925 individuals across the seven phenotypes and the control set.
All analyses assumed an additive effect of a SNP on the phenotype, using a 0/1/2 encoding for each SNP (indicating the number of minor alleles for an individual). The data for each SNP was preprocessed by subtracting the mean and dividing by the standard deviation. A missing SNP observation was set to a value of zero after preprocessing. A likelihood ratio test was used to compute P values. In our test for epistasis, the null model consisted of an additive model with a fixed effect for each SNP, while the alternative model additionally included a fixed effect corresponding to the product of the preprocessed values of each of the two SNPs. In univariate analyses, we used the genome-wide significance threshold from the original analysis (P < 5 × 10−7)5. In the epistatic interaction analyses, we used a Bonferroni-corrected threshold (P < 7.9 × 10−13) for the 63,525,271,461 tested pairs. For comparison, we implemented the epistasis test of Wan et al.1, which also used an LRT, but with different null and alternative models than ours. Their null model was equivalent to a logistic regression on the phenotype using a one-hot encoding of the three states of each SNP (five parameters). Their alternative model was the saturated model—that is, one parameter for each of the 3 × 3 combinations of {0,1,2} × {0,1,2}. Therefore, their final test had four degrees of freedom.
In our analyses, we used a linear mixed model (LMM) with a Gaussian likelihood. Technically, this model is not well suited to the analysis of case-control phenotypes as found in the Wellcome Trust data. Nonetheless, both theoretical and empirical work have demonstrated that use of the Gaussian form performs well on such data8,20. The LMM log likelihood of the phenotype data, y (dimension n × 1), given fixed effects X (dimension n × d), which include the SNP, the covariates and the column of ones corresponding to the bias (offset), can be written as

where  denotes a Normal distribution in r with mean m and covariance matrix Σ; K (dimension n × n) is the genetic similarity matrix; I is the identity matrix;
denotes a Normal distribution in r with mean m and covariance matrix Σ; K (dimension n × n) is the genetic similarity matrix; I is the identity matrix;  (scalar) is the magnitude of the residual variance;
(scalar) is the magnitude of the residual variance;  (scalar) is the magnitude of the genetic variance; and β (dimension d × 1) are the fixed-effect weights.
(scalar) is the magnitude of the genetic variance; and β (dimension d × 1) are the fixed-effect weights.
We used FaST-LMM-Select9,10 for the LMM analyses (code and executables available at http://mscompbio.codeplex.com). The algorithm selected 0, 1, 310, 440, 75, 400 and 29 SNPs for the genetic similarity matrix, for the BD, CAD, CD, HT, RA, T1D and T2D phenotypes, respectively. For the univariate analysis, we used a 2 centimorgan exclusion window to avoid proximal contamination.
We performed the epistatic analyses using 28,000 cores on Windows Azure (http://www.windowsazure.com/en-us/) with the HPC Server Azure burst solution. The runs across all seven phenotypes required 950 compute years, with a wall-clock time of 13 days. Each of the seven runs produced over two terabytes of data.
The calibration of P values was assessed using quantile-quantile plots and the genomic control factor λ. The value λ is defined as the ratio of the median observed test statistic to the median theoretical test statistic under the null distribution. When there is no signal in the data, a calibrated result corresponds to λ = 1.0 and values of λ substantially greater than (less than) 1.0 are indicative of inflation (deflation).
We used chromosome positions to map SNPs to genes. Specifically, we used the latest GRCh37 assembly from UCSC Genome Browser (http://genome.ucsc.edu/) for genes and dbSNP (http://www.ncbi.nlm.nih.gov/projects/SNP/) for SNPs. When a gene had multiple definitions in the UCSC Genome Browser, we chose the one referenced by the HUGO Gene Nomenclature Committee at the European Bioinformatics Institute (http://www.genenames.org).
Change history
18 February 2013
A correction has been published and is appended to both the HTML and PDF versions of this paper. The error has been fixed in the paper.
References
Wan, X. et al. BOOST: A fast approach to detecting gene-gene interactions in genome-wide case-control studies. American journal of human genetics 87, 325–40 (2010).
Wan, X. et al. Predictive rule inference for epistatic interaction detection in genome-wide association studies. Bioinformatics 26, 30–7 (2010).
Hu, X. et al. SHEsisEpi, a GPU-enhanced genome-wide SNP-SNP interaction scanning algorithm, efficiently reveals the risk genetic epistasis in bipolar disorder. Cell Research 20, 854–7 (2010).
Yung, L. S., Yang, C., Wan, X. & Yu, W. GBOOST: a GPU-based tool for detecting gene-gene interactions in genome-wide case control studies. Bioinformatics 27, 1309–10 (2011).
The Wellcome Trust Case Control Genome-wide association study of 14,000 cases of seven common diseases and 3,000 shared controls. Nature 447, 661–78 (2007).
Emily, M., Mailund, T., Hein, J., Schauser, L. & Schierup, M. H. Using biological networks to search for interacting loci in genome-wide association studies. European Journal of Human Genetics 17, 1231–40 (2009).
Yu, J. et al. A unified mixed-model method for association mapping that accounts for multiple levels of relatedness. Nature Genetics 38, 203–8 (2006).
Kang, H. M. et al. Variance component model to account for sample structure in genome-wide association studies. Nature Genetics 42, 348–354 (2010).
Lippert, C. et al. FaST linear mixed models for genome-wide association studies. Nature Methods 8, 833–835 (2011).
Listgarten, J. et al. Improved Linear Mixed Models for Genome-Wide Association Studies. Nature Methods 9, 525–526 (2012).
Li, H., Gao, G., Li, J., Page, G. & Zhang, K. Detecting epistatic interactions contributing to human gene expression using the CEPH family data. BMC Proceedings 1, S67 (2007).
Franke, A. et al. Genome-wide meta-analysis increases to 71 the number of confirmed Crohn's disease susceptibility loci. Nature Genetics 42, 1118–25 (2010).
Evans, D. M., Marchini, J., Morris, A. P. & Cardon, L. R. Two-stage two-locus models in genome-wide association. PLoS Genetics 2, e157 (2006).
Nikitin, A. G., Chistiakov, D. A., Minushkina, L. O., Zateyshchikov, D. A. & Nosikov, V. V. Association of the CYBA, PPARGC1A, PPARG3 and PPARD gene variants with coronary artery disease and metabolic risk factors of coronary atherosclerosis in a Russian population. Heart and Vessels 25, 229–36 (2010).
Roder, C. et al. Common genetic polymorphisms in moyamoya and atherosclerotic disease in Europeans. Child's Nervous System 27, 245–52 (2011).
Balding, D. J. A tutorial on statistical methods for population association studies. Nature Reviews Genetics 7, 781–91 (2006).
Devlin, B. & Roeder, K. Genomic control for association studies. Biometrics 55, 997–1004 (1999).
Yang, J. et al. Genomic inflation factors under polygenic inheritance. European journal of human genetics/: EJHG 19, 807–12 (2011).
Liu, Y. et al. Genome-wide interaction-based association analysis identified multiple new susceptibility Loci for common diseases. PLoS genetics 7, e1001338 (2011).
Agresti, A. Categorical Data Analysis (Wiley: New York, 2002).
Acknowledgements
We thank J. Carlson for help with tools to manage and analyze the data and P. Palamara for cataloging the positions and genetic distances of SNPs in the WTCCC data. This study makes use of data generated by the Wellcome Trust Case-Control Consortium. A full list of the investigators who contributed to the generation of the data is available from www.wtccc.org.uk. Funding for the project was provided by the Wellcome Trust under award 076113 and 085475.
Author information
Authors and Affiliations
Contributions
C.L. and J.L. designed research, contributed analytic tools and wrote the paper. R.D. and S.B. conducted experiments and contributed analytic tools. H.P. conducted experiments and contributed analytic tools. C.K. contributed analytic tools. D.H. designed research, conducted experiments, contributed analytic tools, analyzed data and wrote the paper.
Ethics declarations
Competing interests
All authors were employed by Microsoft while performing this work.
Electronic supplementary material
Supplementary Information
Supplementary Info
Supplementary Information
Supplementary Dataset 1
Supplementary Information
Supplementary Dataset 2
Supplementary Information
Supplementary Dataset 3
Supplementary Information
Supplementary Dataset 4
Rights and permissions
This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivs 3.0 Unported License. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-nd/3.0/
About this article
Cite this article
Lippert, C., Listgarten, J., Davidson, R. et al. An Exhaustive Epistatic SNP Association Analysis on Expanded Wellcome Trust Data. Sci Rep 3, 1099 (2013). https://doi.org/10.1038/srep01099
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep01099
This article is cited by
-
A comparison of methods for interpreting random forest models of genetic association in the presence of non-additive interactions
BioData Mining (2021)
-
Comparative performances of machine learning methods for classifying Crohn Disease patients using genome-wide genotyping data
Scientific Reports (2019)
-
Non-linear interactions between candidate genes of myocardial infarction revealed in mRNA expression profiles
BMC Genomics (2016)
-
Combining Multiple Hypothesis Testing with Machine Learning Increases the Statistical Power of Genome-wide Association Studies
Scientific Reports (2016)
-
Meta-analysis identifies common and rare variants influencing blood pressure and overlapping with metabolic trait loci
Nature Genetics (2016)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.