Abstract
The conventional order parameters in quantum matters are often characterized by ‘spontaneous’ broken symmetries. However, sometimes the broken symmetries may blend with the invariant symmetries to lead to mysterious emergent phases. The heavy fermion metal URu2Si2 is one such example, where the order parameter responsible for a second-order phase transition at Th = 17.5 K has remained a long-standing mystery. Here we propose via ab-initio calculation and effective model that a novel spin-orbit density wave in the f-states is responsible for the hidden-order phase in URu2Si2. The staggered spin-orbit order spontaneously breaks rotational and translational symmetries while time-reversal symmetry remains intact. Thus it is immune to pressure, but can be destroyed by magnetic field even at T = 0 K, that means at a quantum critical point. We compute topological index of the order parameter to show that the hidden order is topologically invariant. Finally, some verifiable predictions are presented.
Similar content being viewed by others
Introduction
Most states or phases of matter can be described by local order parameters and the associated broken symmetries in the spin, charge, orbital or momentum channel. However, recent discoveries of quantum Hall states1 and topological insulators2,3 have revamped this conventional view. It has been realized1,2,3,4 that systems with combined time-reversal ( ) symmetry and large spin-orbit (SO) coupling can host new states of matter which are distinguished by topological quantum numbers of the bulk band structure rather than spontaneously broken symmetries. Subsequently, more such distinct phases have been proposed in the family of topological Mott insulators5, topological Kondo insulators6, topological antiferromagnetic insulators7. In the latter cases, the combined many-body physics and
) symmetry and large spin-orbit (SO) coupling can host new states of matter which are distinguished by topological quantum numbers of the bulk band structure rather than spontaneously broken symmetries. Subsequently, more such distinct phases have been proposed in the family of topological Mott insulators5, topological Kondo insulators6, topological antiferromagnetic insulators7. In the latter cases, the combined many-body physics and  symmetry governs topologically protected quantum phases. Encouraged by these breakthrough developments, we search for analogous exotic phases in the heavy fermion metal URu2Si2, whose low-energy f states accommodate
symmetry governs topologically protected quantum phases. Encouraged by these breakthrough developments, we search for analogous exotic phases in the heavy fermion metal URu2Si2, whose low-energy f states accommodate  and strong SO coupling. This compound also naturally hosts diverse quantum mechanical phases including Kondo physics, large moment antiferromagnetism (LMAF), mysterious ‘hidden-order’ (HO) state and superconductivity8.
and strong SO coupling. This compound also naturally hosts diverse quantum mechanical phases including Kondo physics, large moment antiferromagnetism (LMAF), mysterious ‘hidden-order’ (HO) state and superconductivity8.
In URu2Si2 the screening of f-electrons due to the Kondo effect begins at relatively high temperatures, ushering the system into a heavy fermion metal at low-temperature9. Below Th = 17.5 K, it enters into the HO state via a second-order phase transition characterized by sharp discontinuities in numerous bulk properties10,11,12,13. The accompanying gap is opened both in the electronic structure9,14,15,16 as well as in the magnetic excitation spectrum17, suggesting the formation of an itinerant magnetic order at this temperature. However, the associated tiny moment (~ 0.03µB) cannot account for the large (about 24%) entropy release18 and other sharp thermodynamic10,11 and transport anomalies12,13 during the transition. Furthermore, very different evolutions of the HO parameter and the magnetic moment as a function of both magnetic field19,20 and pressure21,22 rule out a possible magnetic origin of the HO phase in this system. Any compelling evidence for other charge, orbital or structural ordering has also not been obtained23. Existing theories include multiple spin correlator24, Jahn-Teller distortions25, unconventional spin-density wave26,27, antiferromagnetic fluctuation28, orbital order20, helicity order29, staggered quadrupole moment30, octupolar moment31, hexadecapolar order32, linear antiferromagnetic order33, incommensurate hybridization wave34, spin nematic order35, modulated spin liquid36, j-j fluctuations37, unscreened Anderson lattice model38, among others8. However, a general consensus for the microscopic origin of the HO parameter has not yet been attained.
Formulating the correct model for the HO state requires the knowledge of the broken symmetries and the associated electronic degrees of freedom that are active during this transition. A recent torque measurement on high quality single crystal sample reveals that the four-fold rotational symmetry of the crystal becomes spontaneously broken23 at the onset of the HO state. Furthermore, several momentum-resolved spectroscopic data unambiguously indicate the presence of a translational symmetry breaking at a longitudinal incommensurate wavevector Qh = (1±0.4, 0, 0)14,16,18,39. [Previous first-principle calculation has demonstrated that an accompanying commensurate wavevector Q2 = (1, 0, 0) might be responsible for the LMAF phase33, which is separated from the HO state via a first order phase transition8,19,20,21,22. As it is often unlikely to have two phases of same broken symmetry but separated by a phase boundary, we expect that LMAF and HO phases are different.] In general, the order parameter that emerges due to a broken symmetry relies incipiently on the good quantum number and symmetry properties of the ‘parent’ or non-interacting Hamiltonian. In case of URu2Si2, spin and orbital are not the good quantum numbers, rather the presence of the SO coupling renders the total angular momentum to become the good quantum number. Therefore, SU(2) symmetry can not be defined for spin or orbital alone and the ‘parent’ Hamiltonian has to be defined in  representation. The ‘parent’ Hamiltonian also accommodate other symmetries coming from its crystal, wavefunction properties which we desire to incorporate to formulate the HO parameter.
representation. The ‘parent’ Hamiltonian also accommodate other symmetries coming from its crystal, wavefunction properties which we desire to incorporate to formulate the HO parameter.
Results
Ab-initio band structure
In order to find out the symmetry properties of the low-lying states, we begin with investigating the ab-initio ‘parent’ band dispersion and the FS of URu2Si240,41 in Fig. 1. The electronic structure in the vicinity of the Fermi level (EF) (±0.2 eV) is dominated by the 5f states of U atom in the entire Brillouin zone14,15,16,33,39,42. Owing to the SO coupling and the tetragonal symmetry, the 5f states split into the octet  states and the sextet
states and the sextet  states43. URu2Si2 follows a typical band progression in which the Γ8 bands are pushed upward to the empty states while the Γ6 states drop to the vicinity of EF. The corresponding FS in Fig. 1d reveals that an even number of anti-crossing features occurs precisely at the intersection between two oppositely dispersing conducting sheets. Unlike in topological insulators3,4, the departure of the band crossing points from the
states43. URu2Si2 follows a typical band progression in which the Γ8 bands are pushed upward to the empty states while the Γ6 states drop to the vicinity of EF. The corresponding FS in Fig. 1d reveals that an even number of anti-crossing features occurs precisely at the intersection between two oppositely dispersing conducting sheets. Unlike in topological insulators3,4, the departure of the band crossing points from the  -invariant momenta here precludes the opening of an inverted band gap at the crossings2 and Dirac-cones crop up with Kramer's degeneracy in the bulk states. Therefore, URu2Si2 is an intrinsically trivial topological metal above the HO transition temperature.
-invariant momenta here precludes the opening of an inverted band gap at the crossings2 and Dirac-cones crop up with Kramer's degeneracy in the bulk states. Therefore, URu2Si2 is an intrinsically trivial topological metal above the HO transition temperature.
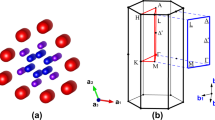
Ab initio band structure and Fermi surface of URu2Si2.
(a) Computed non-interacting energy dispersions of URu2Si2, using Wien2K software40,41, are presented along Γ(0,0,0), X(π,0,0), M(π,π,0) and Z(0,0,π) directions. The band structure is consistent with the previous full potential local orbitals (FPLO) and full potential linearized augmented plane wave (FPLAPW) calculations in the paramagnetic state33. The low-energy dispersions along Γ-X is expanded in (b) and contrasted with the same but without the SO coupling in (c). The FS in the kz = 0 plane is shown in (d). The red arrow dictates the FS ‘hot-spot’ that emerges after including SO coupling.
The SO interaction introduces two prominent FS instabilities at Q2 = (1, 0, 0) and at Qh = (1 ± 0.4, 0, 0). The commensurate wavevector Q2 occurs between same orbital. Therefore, if this instability induces a gap opening, it has to be in the spin-channel, which is prohibited by  symmetry and strong SO coupling. We argue (see Supplementary Information (SI) for details), in accordance with an earlier calculation33, that this instability is responsible for the LMAF phase. On the other hand, the incommensurate one, Qh, occurs between two different orbitals and can open a gap if a symmetry between these orbitals and spins are spontaneously broken together. In other word, since SO coupling is strong in this system, individual spin- or orbital-orderings are unlikely to form unless interaction can overcome the SO coupling strength. On the other hand, a SO entangled order parameter in the two-particle channel can collectively propagate with alternating sign in the total angular momentum at the wavelength determined by the modulation vector. This is the guiding instability that drives spontaneous rotational symmetry breaking, while the
symmetry and strong SO coupling. We argue (see Supplementary Information (SI) for details), in accordance with an earlier calculation33, that this instability is responsible for the LMAF phase. On the other hand, the incommensurate one, Qh, occurs between two different orbitals and can open a gap if a symmetry between these orbitals and spins are spontaneously broken together. In other word, since SO coupling is strong in this system, individual spin- or orbital-orderings are unlikely to form unless interaction can overcome the SO coupling strength. On the other hand, a SO entangled order parameter in the two-particle channel can collectively propagate with alternating sign in the total angular momentum at the wavelength determined by the modulation vector. This is the guiding instability that drives spontaneous rotational symmetry breaking, while the  symmetry remains intact (see Fig. 2a). This is because, both SU(2) groups for spin and orbital separately are odd under
symmetry remains intact (see Fig. 2a). This is because, both SU(2) groups for spin and orbital separately are odd under  , but their product
, but their product  becomes even. As the parent state is not a non-trivial topological phase, a gap is opened to lift the FS instability.
becomes even. As the parent state is not a non-trivial topological phase, a gap is opened to lift the FS instability.
Spin-orbit density wave and the hidden-order gap opening.
(a) A typical form of the staggered SO order is schematically described for an illustrative case of commensurate wavevector. The solid and dashed circles encode two opposite orbitals, τ = ±, where the associated arrows depict their ‘pseudospins’ σ. Both τ and σ, representing orbital and spin respectively, individually break  symmetry, while their product remains
symmetry, while their product remains  invariant. (b) Model dispersions of the
invariant. (b) Model dispersions of the  and
and  subbands plotted along the axial direction. Black and red lines give dispersion before and after including the HO gap, respectively. An artificially large value of Δ = 50 meV is chosen here to clearly explicate the momentum dependence of the modulated SO gap opening. (c) Modifications of DOS upon entering into the HO phase are compared with measured DOS in the STM experiment (green line)14. Note that the experimental data is subtracted from the background spectrum at T>Th, which helps highlight the appearance of multiple structures in the DOS spectrum at the HO state. Here the gap magnitude Δ(0) = 5 meV, obtained at a coupling strength of g = 27 meV, see SI. Inset: The self-consistent value of Δ(T) exhibits the mean-field behavior of the HO gap, in consistent with experiments9. We obtain Th = 22 K which is larger than the experimental value of Th = 17.5 K. However, recently it has been pointed out that there exists a ‘pseudogap’ above the HO state58, which presumably reduces the mean-field temperature scale. (d) RPA result of SO correlation function at g = 28.4 meV shows a resonance peak at ωQ = 4.7 meV at Qh, in good agreement with experimental data18,59.
subbands plotted along the axial direction. Black and red lines give dispersion before and after including the HO gap, respectively. An artificially large value of Δ = 50 meV is chosen here to clearly explicate the momentum dependence of the modulated SO gap opening. (c) Modifications of DOS upon entering into the HO phase are compared with measured DOS in the STM experiment (green line)14. Note that the experimental data is subtracted from the background spectrum at T>Th, which helps highlight the appearance of multiple structures in the DOS spectrum at the HO state. Here the gap magnitude Δ(0) = 5 meV, obtained at a coupling strength of g = 27 meV, see SI. Inset: The self-consistent value of Δ(T) exhibits the mean-field behavior of the HO gap, in consistent with experiments9. We obtain Th = 22 K which is larger than the experimental value of Th = 17.5 K. However, recently it has been pointed out that there exists a ‘pseudogap’ above the HO state58, which presumably reduces the mean-field temperature scale. (d) RPA result of SO correlation function at g = 28.4 meV shows a resonance peak at ωQ = 4.7 meV at Qh, in good agreement with experimental data18,59.
Low-energy effective model
Motivated by the above-mentioned experimental results and band structure symmetry properties, we formulate a simple and unified model by using the theory of invariants44. We restrict our discussion to the low-lying Γ6 bands and neglect the unfilled Γ8 bands. Due to j-j SO coupling and  symmetry, the Γ6 atomic states consist of three doublets, characterized by up and down ‘pseudospins’:
symmetry, the Γ6 atomic states consist of three doublets, characterized by up and down ‘pseudospins’:  ,
,  ,
,  , where mJ is the z component of J. On entering into the HO state, the FS instability commences in between the two doubly degenerate
, where mJ is the z component of J. On entering into the HO state, the FS instability commences in between the two doubly degenerate  and
and  states only33,35. If no other symmetry is broken, the degenerate
states only33,35. If no other symmetry is broken, the degenerate  state remains unaltered in the HO state44 and hence they are not considered in our model Hamiltonian. Throughout this paper, we consistently use two indices: orbital index
state remains unaltered in the HO state44 and hence they are not considered in our model Hamiltonian. Throughout this paper, we consistently use two indices: orbital index  and ‘pseudospin’ σ = ↑(+), ↓(−). In this notation, we consider the ‘pseudospinor’ field
and ‘pseudospin’ σ = ↑(+), ↓(−). In this notation, we consider the ‘pseudospinor’ field  , where
, where  is the creation operator for an electron in the orbital
is the creation operator for an electron in the orbital  with momentum k and ‘pseudospin’ σ.
with momentum k and ‘pseudospin’ σ.
The representation of the symmetry operations that belongs to the D4h symmetry of the URu2Si2 crystal structure is:  symmetry, inversion symmetry
symmetry, inversion symmetry  , four-fold rotational symmetry
, four-fold rotational symmetry  and the two reflection symmetries
and the two reflection symmetries  . The SO f-state of actinides is invariant under all symmetries except the mirror reflection, which in fact allows the formation of the SO density wave into a finite gap in the HO state (see SI). On the basis of these symmetry considerations, it is possible to deduce the general form of the non-interacting Hamiltonian as:
. The SO f-state of actinides is invariant under all symmetries except the mirror reflection, which in fact allows the formation of the SO density wave into a finite gap in the HO state (see SI). On the basis of these symmetry considerations, it is possible to deduce the general form of the non-interacting Hamiltonian as:


Here, τµ (µ  0, x, y, z) depict the 2D Pauli matrices in the orbital space and τ0 is the identity matrix (σµ matrices will be used later to define the spin space). The
0, x, y, z) depict the 2D Pauli matrices in the orbital space and τ0 is the identity matrix (σµ matrices will be used later to define the spin space). The  invariance requires that
invariance requires that  . Under
. Under  and
and  , the symmetry of
, the symmetry of  and
and  must complement to their corresponding identity and Pauli Matrix counterparts, respectively. Hence we obtain the Slater-Koster hopping terms as:
must complement to their corresponding identity and Pauli Matrix counterparts, respectively. Hence we obtain the Slater-Koster hopping terms as:  and
and  . The obtained values of the tight-binding hopping parameters as (t, t1, t2, tz) = −(−45,45,50,−25) in meV. The above Hamiltonian can be solved analytically which gives rise to four SO-split energy dispersions as
. The obtained values of the tight-binding hopping parameters as (t, t1, t2, tz) = −(−45,45,50,−25) in meV. The above Hamiltonian can be solved analytically which gives rise to four SO-split energy dispersions as

Here σ = ± and τ = ± become band indices. An important difference of the present Hamiltonian with that of bulk topological insulators3 or quantum spin-Hall systems1 is the absence of a mass or gap parameter in the former case. The computed non-interacting bands are plotted in Fig. 2b, which exhibit several Dirac points along the high-symmetry lines. Focusing on the Dirac point close to EF, we find that it occurs at the crossing between bands E+− and E−+, demonstrating that it hosts four-fold Kramer's degeneracy (two orbitals and two spins). Therefore, lifting this degeneracy requires the presence of a SO order parameter. However, it is important to note that the gap opening at the Dirac point is not a manifestation of the presence of degeneracy at it, but a consequence of the SO density wave caused by FS instability.
SO density wave induced HO
The ‘hot-spot’ Qh divides the unit cell into a reduced ‘SO Brillouin zone’ in which we can define the Nambu operator in the usual way  . In this notation, the SO density wave (SODW) interaction term can be written in general as
. In this notation, the SO density wave (SODW) interaction term can be written in general as

where µ, ν ∈ {0, x, y, z}. The symbol :: represents normal ordering. Here g is the contact coupling interaction arising from screened interorbital Coulomb term embedded in Hund's coupling parameter and  , τ and σ represent Pauli matrices in orbital and spin basis, respectively. Absorbing g and Γ into one term we define the mean-field order parameter
, τ and σ represent Pauli matrices in orbital and spin basis, respectively. Absorbing g and Γ into one term we define the mean-field order parameter

Here τ, τ′ and σ, σ′ (not in bold font) are the components of the τµ and σν matrices, respectively. Without any loss of generality we fix the spin orientation along z-directions (ν = z). Therefore, we drop the index ν henceforth. Furthermore we define the gap vector as  , where we split the interaction term g(k) into a constant onsite term and the dimensionless order parameter Δ(k). With these substitutions, we obtain the final result for the order parameter as
, where we split the interaction term g(k) into a constant onsite term and the dimensionless order parameter Δ(k). With these substitutions, we obtain the final result for the order parameter as

Eq. 7 admits a plethora of order parameters related to the SO density wave formations which break symmetry in different ways. Among them, we rule out those parameters which render gapless states by using the symmetry arguments (see SI): All four order parameters obey  symmetry, while only My term is even under
symmetry, while only My term is even under  , because it is the product of two odd terms τy and σ (we drop the superscript ‘y’ henceforth). This is the only term which commences a finite gap opening if the translational or rotational symmetry is spontaneously broken. We have shown in SI that there exists a considerably large parameter space of coupling constant ‘g’ where this order parameter dominates.
, because it is the product of two odd terms τy and σ (we drop the superscript ‘y’ henceforth). This is the only term which commences a finite gap opening if the translational or rotational symmetry is spontaneously broken. We have shown in SI that there exists a considerably large parameter space of coupling constant ‘g’ where this order parameter dominates.
Eq. 7 implies that spin and orbital orderings occur simultaneously along the ‘hot-spot’ direction Qh, as illustrated in Fig. 2a. It propagates along  or
or  directions with alternating signs (particle-hole pairs) to commence a SO density wave. The resulting Hamiltonian breaks the four-fold rotational symmetry down to a two-fold one
directions with alternating signs (particle-hole pairs) to commence a SO density wave. The resulting Hamiltonian breaks the four-fold rotational symmetry down to a two-fold one  and gives rise to a so-called spin-orbit ‘smectic’ state which breaks both translational and C4 symmetry45. The present
and gives rise to a so-called spin-orbit ‘smectic’ state which breaks both translational and C4 symmetry45. The present  invariant SO order parameter is inherently distinct from any spin or orbital or even interorbital spin-density wave order which break
invariant SO order parameter is inherently distinct from any spin or orbital or even interorbital spin-density wave order which break  symmetry. This criterion also rules out any similarly between our present SO smectic state with the spin-nematic phase35 or spin-liquid state36. Furthermore, the present order parameter is different from
symmetry. This criterion also rules out any similarly between our present SO smectic state with the spin-nematic phase35 or spin-liquid state36. Furthermore, the present order parameter is different from  invariant ‘hybridization wave’ (between f and d orbitals of same spin), or charge density wave or others30,32, as SO order involves flipping of both orbital (between split f orbitals that belong to Γ6 symmetry) and spin simultaneously. Taking into account the band-structure information that Qh represents the interband nesting, it is instructive to focus on only b12(k) component (thus the subscript ‘12’ is eliminated hereafter). Therefore, the SO density wave does not introduce a spin or orbital moment, but a polarization in the total angular momentum δmJ = ±2 [for the ordering between
invariant ‘hybridization wave’ (between f and d orbitals of same spin), or charge density wave or others30,32, as SO order involves flipping of both orbital (between split f orbitals that belong to Γ6 symmetry) and spin simultaneously. Taking into account the band-structure information that Qh represents the interband nesting, it is instructive to focus on only b12(k) component (thus the subscript ‘12’ is eliminated hereafter). Therefore, the SO density wave does not introduce a spin or orbital moment, but a polarization in the total angular momentum δmJ = ±2 [for the ordering between  and
and  ].
].
The b vector belongs to the same irreducible point group representation, Eg, of the crystal with odd parity and can be defined by |b(k)| = 2igΔx sin kxa, or 2igΔy sin kya for the wavevectors  , or
, or  , respectively. The mean-field Hamiltonian for the HO state within an effective two band model reduces to the general form HMF = H0+HSODW, where the particle-hole coupling term is
, respectively. The mean-field Hamiltonian for the HO state within an effective two band model reduces to the general form HMF = H0+HSODW, where the particle-hole coupling term is

In the Nambu representation, it is obvious that the HO term merely adds a mass term to the  term defined above. At the band-crossing points located where
term defined above. At the band-crossing points located where  , a gap opens by the value of |b(k)|2. Figure 2 demonstrates the development of the quasi-particle structure in the HO state. The band progression and the associated gap opening is fully consistent with the angle-resolved photoemission spectroscopy (ARPES) observations15,16. The scanning tunneling microscopy and spectroscopic (STM/S)9,14 fingerprints of the gap opening in the density of state (DOS) is also described nicely within our calculations, see Fig. 2c.
, a gap opens by the value of |b(k)|2. Figure 2 demonstrates the development of the quasi-particle structure in the HO state. The band progression and the associated gap opening is fully consistent with the angle-resolved photoemission spectroscopy (ARPES) observations15,16. The scanning tunneling microscopy and spectroscopic (STM/S)9,14 fingerprints of the gap opening in the density of state (DOS) is also described nicely within our calculations, see Fig. 2c.
Discussion
The SO moment is  , where
, where  is imaginary time. Introducing simplified indices α, β = ττ′σσ′, the correlation function of
is imaginary time. Introducing simplified indices α, β = ττ′σσ′, the correlation function of  vector can be defined as
vector can be defined as  , where
, where  is normal time-ordering. Our numerical calculation of the
is normal time-ordering. Our numerical calculation of the  within random-phase approximation (RPA) yields an inelastic neutron scattering (INS) mode with enhanced intensity at Qh near ωQ ~ 4.7 meV below Th as shown in Fig. 1d. INS data (symbols) at a slightly large momentum agrees well with our calculation, however, a polarized INS measurement will be of considerable value to distinguish our proposed
within random-phase approximation (RPA) yields an inelastic neutron scattering (INS) mode with enhanced intensity at Qh near ωQ ~ 4.7 meV below Th as shown in Fig. 1d. INS data (symbols) at a slightly large momentum agrees well with our calculation, however, a polarized INS measurement will be of considerable value to distinguish our proposed  invariant mode from any spin-flip and elastic background46. A T-dependent study of the INS mode also reveals that this mode becomes strongly enhanced at Qh rather than at the commensurate one below Th39.
invariant mode from any spin-flip and elastic background46. A T-dependent study of the INS mode also reveals that this mode becomes strongly enhanced at Qh rather than at the commensurate one below Th39.
One way to characterize the nature of a phase transition is to determine the temperature evolution of the gap value. Our computed self-consistent values of the mean-field gap Δ(T) agree well with the extracted gap values from the STM spectra9 [see inset to Fig. 2c]. In general, the entropy loss at a mean-field transition is given by20  , where Δ is the HO gap and ξF is the Fermi energy of the gapped state. At HO the Fermi energy
, where Δ is the HO gap and ξF is the Fermi energy of the gapped state. At HO the Fermi energy  , where the two linearly dispersive bands near the Fermi level yields
, where the two linearly dispersive bands near the Fermi level yields  . Using the measured Sommerfield coefficient γ = 180 mJmol−1K−2, compared to its linear expansion of γ0 = 50 mJmol−1K−2, we obtain the mass renormalization factor Z−1 = γ/γ0 = 3.6. This gives
. Using the measured Sommerfield coefficient γ = 180 mJmol−1K−2, compared to its linear expansion of γ0 = 50 mJmol−1K−2, we obtain the mass renormalization factor Z−1 = γ/γ0 = 3.6. This gives  . For the two bands that participate in the HO gap opening, we get
. For the two bands that participate in the HO gap opening, we get  in eV at k1F = 0.5π/a and
in eV at k1F = 0.5π/a and  in eV at k2F = 0.3π/a from Fig. 1a. Using the experimental value of Δ = 5 meV9,14, we obtain ΔS~ 0.28kB ln 2, which is close the experimental value of 0.3kB ln 210.
in eV at k2F = 0.3π/a from Fig. 1a. Using the experimental value of Δ = 5 meV9,14, we obtain ΔS~ 0.28kB ln 2, which is close the experimental value of 0.3kB ln 210.
We now evaluate the topological invariant index of interacting Hamiltonian in Eq. 8 to demonstrate that HO gap opening in URu2Si2 also induces topological phase transition. To characterize the topological phenomena, we recall the Fu-Kane classification scheme2 which implies that if a time-reversal invariant system possess an odd value of Z2 invariant index, the system is guaranteed to be topologically non-trivial. Z2 index is evaluated by the time-reversal invariant index νi = ±1, if defined, for all filled bands as Z2 = ν1ν2…νn, where n is the total number of orbitals in the Fermi sea. A more efficient method of determining the topological phase is called the adiabatic transformation scheme used earlier in realizing a large class of topological systems, especially when Z2 calculation is difficult47. In this method, the non-trivial topological phase of a system can be realized by comparing its band-progression with respect to an equivalent trivial topological system. URu2Si2 is topologically trivial above the HO state, i.e.  . The gap opening makes the top of the valence band (odd parity) to drop below EF as shown in Fig. 2b. Thereby, an odd parity gained in the occupied level endows the system to a non-trivial topological metal. To see that we evaluate the topological index for the HO term as νho = ∫ dkΩ(k), where the corresponding Berry curvature can be written in terms of b-vector as
. The gap opening makes the top of the valence band (odd parity) to drop below EF as shown in Fig. 2b. Thereby, an odd parity gained in the occupied level endows the system to a non-trivial topological metal. To see that we evaluate the topological index for the HO term as νho = ∫ dkΩ(k), where the corresponding Berry curvature can be written in terms of b-vector as  for each spin with
for each spin with  . Due to the odd parity symmetry of b, it is easy to show that νho = −1 which makes the total Z2 value of the HO phase to be
. Due to the odd parity symmetry of b, it is easy to show that νho = −1 which makes the total Z2 value of the HO phase to be  and hence we show that hidden order gapping is a topologically non-trivial phase. The consequence of a topological bulk gap is the presence of surface states2,47. In our present model, we expect two surface states of opposite spin connecting different orbitals inside the HO gap. As the system is a weak-topological system, the surface states are unlikely to be topologically protected. The SO locking of these states can be probed by ARPES using circular polarized incident photon which will be a definite test of this postulate.
and hence we show that hidden order gapping is a topologically non-trivial phase. The consequence of a topological bulk gap is the presence of surface states2,47. In our present model, we expect two surface states of opposite spin connecting different orbitals inside the HO gap. As the system is a weak-topological system, the surface states are unlikely to be topologically protected. The SO locking of these states can be probed by ARPES using circular polarized incident photon which will be a definite test of this postulate.
The HO gap is protected from any  invariant perturbation such as pressure (with sufficient pressure the HO transforms into the LMAF phase), while
invariant perturbation such as pressure (with sufficient pressure the HO transforms into the LMAF phase), while  breaking perturbation such as magnetic field will destroy the order. Remarkably, these are the hallmark features of the HO states23,35,48, which find a natural explanation within our SO density wave order scenario. In what follows, the magnetic field will destroy the HO state even at T = 0 K, that means at a quantum critical point (QCP) as the HO is a spontaneously broken symmetry phase49. However, due to the finite gap opening at the HO state, it requires finite field to destroy the order. The thermodynamical critical field can be obtained from50
breaking perturbation such as magnetic field will destroy the order. Remarkably, these are the hallmark features of the HO states23,35,48, which find a natural explanation within our SO density wave order scenario. In what follows, the magnetic field will destroy the HO state even at T = 0 K, that means at a quantum critical point (QCP) as the HO is a spontaneously broken symmetry phase49. However, due to the finite gap opening at the HO state, it requires finite field to destroy the order. The thermodynamical critical field can be obtained from50  , where Bc is the critical field and
, where Bc is the critical field and  at the resonance mode that develops in the HO state. α = gµB|〈ΔmJ〉| = 2gµB and bare g-factor g = 0.8. Substituting ωres = 4.7 meV, we get the location of the QCP at B ≈ 38 T, which is close the experimental value of B = 34 T48.
at the resonance mode that develops in the HO state. α = gµB|〈ΔmJ〉| = 2gµB and bare g-factor g = 0.8. Substituting ωres = 4.7 meV, we get the location of the QCP at B ≈ 38 T, which is close the experimental value of B = 34 T48.
Broken symmetry FS reconstruction leads to enhanced Nernst signal51. For the case of broken symmetry SO order, we expect to generate spin-resolved Nernst effect which can be measured in future experiments to verify our proposal52.
In summary, we proposed a novel SO density wave order parameter for the HO state in URu2Si2. Such order parameter is  symmetry invariant. We find no fundamental reason why such order parameter cannot develop in other systems in which both electronic correlation and SO of any kind are strong. Some of the possible materials include heavy fermion systems, Iridates53, SrTiO3 surface states54, SrTiO3/LiAlO3 interface55, Half-Heusler topological insulator47 and other d- and f-electron systems with strong SO. In particular, a Rashba-type SO appears due to relativistic effect in two-dimensional electron system yielding helical FSs. In such systems, the FS instability may render similar SO density wave and the resulting quasiparticle gap opening is observed on the surface state of BiAg2 alloys even when the spin-degeneracy remains intact56. Furthermore, recent experimental findings of quasiparticle gapping in the surface state of topological insulator due to quantum phase transition even in the absence of time-reversal symmetry breaking can also be interpreted as the development of some sort of spin orbit order57.
symmetry invariant. We find no fundamental reason why such order parameter cannot develop in other systems in which both electronic correlation and SO of any kind are strong. Some of the possible materials include heavy fermion systems, Iridates53, SrTiO3 surface states54, SrTiO3/LiAlO3 interface55, Half-Heusler topological insulator47 and other d- and f-electron systems with strong SO. In particular, a Rashba-type SO appears due to relativistic effect in two-dimensional electron system yielding helical FSs. In such systems, the FS instability may render similar SO density wave and the resulting quasiparticle gap opening is observed on the surface state of BiAg2 alloys even when the spin-degeneracy remains intact56. Furthermore, recent experimental findings of quasiparticle gapping in the surface state of topological insulator due to quantum phase transition even in the absence of time-reversal symmetry breaking can also be interpreted as the development of some sort of spin orbit order57.
References
Bernevig, B. A., Hughes, T. L. & Zhang, S. C. Quantum spin Hall effect and topological phase transition in HgTe quantum wells. Science 314, 1757 (2006).
Fu, L., Kane, C. L. & Mele, E. J. Topological insulators in three dimensions. Phys. Rev. Lett. 98, 106803 (2007).
Zhang, H. et al. Topological insulators in Bi2Se3, Bi2Te3 and Sb2Te3 with a single Dirac cone on the surface. Nat. Phys. 5, 438 (2009).
Hsieh, D. et al. A tunable topological insulator in the spin helical Dirac transport regime. Nature 460, 1101 (2009).
Raghu, S., Qi, X. L., Honerkamp, C. & Zhang, S. C. Topological Mott insulators. Phys. Rev. Lett. 100, 156401 (2008).
Dzero, M., Sun, K., Galitski, V. & Coleman, P. Topological Kondo insulators. Phys. Rev. Lett. 104, 106408 (2010).
Mong, R. S. K., Essin, A. M. & Moore, J. E. Antiferromagnetic topological insulators. Phys. Rev. B 81, 245209 (2010).
Mydosh, J. A. & Oppeneer, P. M. Colloquium: Hidden order, superconductivity and magnetism – the unsolved case of URu2Si2 . Rev. Mod. Phys. 83, 1301 (2011).
Aynajiana, P. et al. Visualizing the formation of the Kondo lattice and the hidden order in URu2Si2 . Proc. Natl. Acad. Sci. USA 107, 10383 (2010).
Palstra, T. T. M. et al. Superconducting and magnetic transitions in the heavy-fermion system URu2Si2 . Phys. Rev. Lett. 55, 2727 (1985).
Palstra, T. T. M. et al. Anisotropic electrical resistivity of the magnetic heavy-fermion superconductor URu2Si2 . Phys. Rev. B 33, 6527 (1986).
Ramirez, A. P. et al. Nonlinear susceptibility as a probe of tensor spin order in URu2Si2 . Phys. Rev. Lett. 68, 2680 (1992).
Visser, A. D. et al. Thermal expansion and specific heat of monocrystalline URu2Si2 . Phys. Rev. B 34, 8168 (1986).
Schmidt, A. R. et al. Imaging the Fano lattice to a hidden order transition in URu2Si2 . Nature 465, 570 (2010).
Santander-Syro, A. F. et al. Fermi-surface instability at the ‘hidden-order’ transition of URu2Si2 . Nat. Phys. 5, 637 (2009).
Yoshida, R. et al. Signature of hidden order and evidence for periodicity modification in URu2Si2 . Phys. Rev. B 82, 205108 (2010).
Mason, T. E. & Buyers, W. J. L. Spin excitations and the electronic-specific heat of URu2Si2 . Phys. Rev. B 43, 11471 (1991).
Broholm, C. et al. Magnetic excitations and ordering in the heavy-electron superconductor URu2Si2 . Phys. Rev. B 43, 12809 (1991).
Mentink, S. A. M. et al. Gap formation and magnetic ordering in URu2Si2 probed by high-field magnetoresistance. Phys. Rev. B 53, 6014(R) (1996).
Chandra, P. et al. Hidden orbital order in the heavy fermion metal URu2Si2 . Nature 417, 831-834 (2002).
Amitsuka, H. et al. Effect of pressure on tiny antiferromagnetic moment in the heavy-electron compound URu2Si2 . Phys. Rev. Lett. 83, 5114 (1999).
Fisher, R. A. et al. Specific heat of URu2Si2: Effect of pressure and magnetic field on the magnetic and superconducting transitions. Physica B. 163, 419 (1990).
Okazaki, R. et al. Rotational symmetry breaking in the hidden-order phase of URu2Si2 . Science 331, 439 (2011).
Barzykin, V. & Goŕkov, L. P. Possibility of observation of nontrivial magnetic order by elastic neutron scattering in magnetic field. Phys. Rev. Lett. 70, 2479 (1993).
Kasuya, T. et al. Hidden ordering and heavy mass in URu2Si2 and its alloys. J. Phys. Soc. Jpn. 66, 3348 (1997).
Ikeda, H. & Ohashi, Y. Theory of unconventional spin density wave: A possible mechanism of the micromagnetism in U-based heavy fermion compounds. Phys. Rev. Lett. 81, 3723 (1998).
Mineev, V. P. & Zhitomirsky, M. E. Interplay between spin-density wave and induced local moments in URu2Si2 . Phys. Rev. B 72, 014432 (2005).
Okuno, Y. & Miyake, K. Induced-moment weak antiferromagnetism and orbital order on the itinerantlocalized duality model with nested FS : A possible origin of exotic magnetism in URu2Si2 . J. Phys. Soc. Jpn. 67, 2469 (1998).
Varma, C. M. & Zhu, L. Helicity order: Hidden order parameter in URu2Si2 . Phys. Rev. Lett. 96, 036405 (2006).
Santini, P. Behavior of URu2Si2 in an applied magnetic field. Phys. Rev. B 57, 5191-5199 (1998).
Hanzawa, K. Hidden octupole order in URu2Si2 . J. Phys.: Condens. Matter 19, 072202 (2007).
Haule, K. & Kotliar, G. Arrested Kondo effect and hidden order in URu2Si2 . Nat. Phys. 5, 796–799 (2009).
Elgazzar, S. et al. Hidden order in URu2Si2 originates from FS gapping induced by dynamic symmetry breaking. Nat. Mat. 8, 337–341 (2009).
Dubi, Y. & Balatsky, A. V. Hybridization wave as the hidden order in URu2Si2 . Phys. Rev. Lett. 106, 086401 (2011).
Fujimoto, S. Spin nematic state as a candidate of the hidden order phase of URu2Si2 . Phys. Rev. Lett. 106, 196407 (2011).
Pépin, C. et al. Modulated spin liquid: A new paradigm for URu2Si2 . Phys. Rev. Lett. 106, 106601 (2011).
Oppeneer, P. M. et al. Spin and orbital hybridization at specifically nested FSs in URu2Si2 . Phys. Rev. B 84, 241102(R) (2011).
Riseborough, P. S. et al. Phase transition arising from the underscreened Anderson lattice model: A candidate concept for explaining hidden order in URu2Si2 . Phys. Rev. B 85, 165116 (2012).
Wiebe, C. R. et al. Gapped itinerant spin excitations account for missing entropy in the hidden-order state of URu2Si2 . Nat. Phys. 3, 96 (2007).
Blaha, P. et al. An augmented plane wave plus local orbitals program for calculating crystal properties. (Techn. Univ. Wien) (2001).
Perdew, J. P. et al. Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865 (1996).
Denlinger, J. D. et al. Comparative Study of the Electronic Structure of X Ru2Si2: Probing the Anderson Lattice. J. Elect. Spect. Relat. Phenom. 117, 347 (2001).
Hotta, T. & Ueda, K. Construction of a microscopic model for f electron systems on the basis of a j – j coupling scheme. .Phys. Rev. B 67, 104518 (2003).
Winkler, R. Spin-orbit coupling effects in two dimensional electron and hole systems. (Springer Tracts in Modern Physics, Vol. 191, Springer (2003).
Zaanen, J. & Gunnarsson, O. Charged magnetic domain lines and the magnetism of high-Tc oxides. Phys. Rev. B 40, 7391–394 (1989).
Fauqué, B. et al. Magnetic order in the pseudogap phase of high-TC superconductors. Phys. Rev. Lett. 96, 197001 (2006).
Lin, H. et al. Half-Heusler ternary compounds as new multifunctional experimental platforms for topological quantum phenomena. Nature Materials 9, 546 (2010).
Kim, K. H. et al. Magnetic-field-induced quantum critical point and competing order parameters in URu2Si2 . Phys. Rev. Lett. 91, 256401 (2003).
Sachdev, S. Quantum phase transitions. .Cambridge University Press, Cambridge U.K. (1999).
Pathria, R. K. Statistical Mechanics, .Butterworth-Heinemann publishers, 2nd Edition, 1996).
Oganesyan, V. & Ussishkin, I. Nernst effect, quasiparticles and d–density waves in cuprates. .Phys. Rev. B 70, 054503 (2004).
Cheng, S.-G., Xing, Y., Sun, Q. & Xie, X. C. Spin Nernst effect and Nernst effect in twodimensional electron systems. Phys. Rev. B 78, 045302 (2008).
Witczak-Krempa, W. & Kim, Y. B. Topological and magnetic phases of interacting electrons in the pyrochlore iridates. Phys. Rev. B 85, 045124 (2012).
Santander-Syro, A. F. et al. Two-dimensional electron gas with universal subbands at the surface of SrTiO3 . Nature 469, 189–193 (2011).
Caviglia, A. D. et al. Tunable Rashba spin-orbit interaction at Oxide interfaces. Phys. Rev. Lett. 104, 126803 (2010).
Bentmann, H. et al. Direct observation of interband spin-orbit coupling in a two-dimensional electron system. Phys. Rev. Lett. 108, 196801 (2012).
Sato, E. et al. Unexpected mass acquisition of Dirac fermions at the quantum phase transition of a topological insulator. Nat. Phys. 7, 840 (2011).
Haraldsen, J. T. et al. Hidden-order pseudogap in URu2Si2 . Phys. Rev. B 84, 214410 (2011).
Bourdarot, F. et al. Precise study of the resonance at Q0 = (1, 0, 0) in URu2Si2 . J. Phys. Soc. Jap. 79, 064719 (2010).
Acknowledgements
The author thanks A. V. Balatsky, M. J. Graf, A. Bansil, R. S. Markiewicz, T. Durakiewicz, J.-X. Zhu, P. M. Oppeneer, J. Mydosh, P. Wölfle and J. Haraldsen for useful discussions. Work at the Los Alamos National Laboratory was supported by the U.S. DOE under contract no. DE-AC52-06NA25396 through the Office of Basic Energy Sciences and the UC Lab Research Program and benefited from the allocation of supercomputer time at NERSC.
Author information
Authors and Affiliations
Contributions
TD has carried out all the calculations, prepared the figures, wrote the paper.
Ethics declarations
Competing interests
The author declares no competing financial interests.
Electronic supplementary material
Supplementary Information
Detailed formalism
Rights and permissions
This work is licensed under a Creative Commons Attribution 3.0 Unported License. To view a copy of this license, visit http://creativecommons.org/licenses/by/3.0/
About this article
Cite this article
Das, T. Spin-orbit density wave induced hidden topological order in URu2Si2. Sci Rep 2, 596 (2012). https://doi.org/10.1038/srep00596
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep00596
This article is cited by
-
Distinct itinerant spin-density waves and local-moment antiferromagnetism in an intermetallic ErPd2Si2 single crystal
Scientific Reports (2015)
-
Observation of correlated spin–orbit order in a strongly anisotropic quantum wire system
Nature Communications (2015)
-
Tuning the vertical location of helical surface states in topological insulator heterostructures via dual-proximity effects
Scientific Reports (2013)
-
Staggered Spin-Orbit Order: A New Paradigm of Broken Symmetry Phase of Matter
Journal of Superconductivity and Novel Magnetism (2013)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.