Abstract
Electronic properties of DNA are believed to play a crucial role in many phenomena in living organisms, for example the location of DNA lesions by base excision repair (BER) glycosylases and the regulation of tumor-suppressor genes such as p53 by detection of oxidative damage. However, the reproducible measurement and modelling of charge migration through DNA molecules at the nanometer scale remains a challenging and controversial subject even after more than a decade of intense efforts. Here we show, by analysing 162 disease-related genes from a variety of medical databases with a total of almost 20,000 observed pathogenic mutations, a significant difference in the electronic properties of the population of observed mutations compared to the set of all possible mutations. Our results have implications for the role of the electronic properties of DNA in cellular processes and hint at the possibility of prediction, early diagnosis and detection of mutation hotspots.
Similar content being viewed by others
Introduction
Cells tend to accumulate over time genetic changes such as nucleotide substitutions, small insertions and deletions, rearrangements of the genetic sequences and copy number changes1. These changes in turn affect protein-coding or regulatory components and lead to health issues such as cancer, immunodeficiency, ageing-related diseases and other disorders. A cell responds to genetic damage by initiating a repair process or programmed cell death2. In recent years, a vast number of detailed databases have been assembled in which rich information about the type, severity, frequency and diagnosis of many thousand of such observed mutations has been stored3,4,5,6. This abundance of data is based on the now standard availability of massively parallel sequencing technologies7. Harvesting these genomic databases for new cancer genes and hence potential therapeutic targets has already demonstrated its usefulness8 and several recent international cancer genome projects continue the required large-scale analysis of genes in tumours9.
The possible relevance of charge transport in DNA damage has recently also attracted considerable interest in the bio-chemical and bio-physical literature10,11,12,13. Direct measurement of charge transport and/or transfer in DNA remains a highly controversial topic due to the very challenging level of required manipulation at the nano-scale14. Ab-initio modelling of long DNA strands is similarly demanding of computational resources and so some of the most promising computational approaches necessarily use much simplified models based on coarse-grained DNA.11 Here we compute and datamine the results of charge transport calculations based on two such effective models for each possible mutation in 162 of the most important disease-associated genes from four large gene databases. The models are (i) the standard one-dimensional chain of coupled nucleic bases with onsite ionisation potentials11,15 as well as a novel 2-leg ladder model with diagonal couplings and explicit modelling of the sugar-phosphate backbone16.
Results
Point Mutations and Electronic Properties
We consider native genetic sequences and mutations of disease-associated genes as retrieved from the Online Mendelian Inheritance in Man (OMIM)3 of NCBI, the Human Gene Mutation Database (HGMD)4, the International Agency of Research on Cancer (IARC)5 as well as Retinoblastoma Genetics6. We have selected these genes such that (i) those from OMIM have a well-known sequence with known phenotype as well as at least 10 point mutations, (ii) all other selected cancer-related genes have also at least 10 point mutations and (iii) all non-cancer related genes from HGMD have at least 200 point mutations (cp. Supplementary Table S1).
Many different types of mutation are possible in a genetic sequence including point mutations, deletion of single base pairs (producing a frame shift) and large-scale deletion or duplication of multiple base pairs. Here, we restrict our attention to point mutations as it allows us to directly compare the sequence before and after the mutation. This leaves us with in total 19882 such mutations. We study the magnitude of the change in charge transport (CT) for pathogenic mutations when compared to all possible mutations either locally, i.e. at the given hotspot site, or globally when ranked according to magnitude of CT change. We find that the vast majority of mutations shows good agreement with a hypothesis where smallest change in electronic properties — as measured by a change in CT — corresponds to a mutation that has appeared in one of the aforementioned databases of pathogenic genes.
A gene with  base pairs (bps) has a native nucleotide sequence
base pairs (bps) has a native nucleotide sequence  along the coding strand with si denoting one of the 4 possible nucleotide bases A,C,G,T. The gene has a total of
along the coding strand with si denoting one of the 4 possible nucleotide bases A,C,G,T. The gene has a total of  possible point mutations, which we denote as the set Mall, of which a subset Mpa are known pathogenic mutations. A point mutation is represented by the pair (k, s), where k is the position of the point mutation in the genomic sequence and s is the mutant nucleotide which replaces the native nucleotide. We shall write a mutation from a native base P to a mutant base Q as “Pq”. We note that there are a total of twelve possible point mutations for each nucleotide position in a DNA sequence (from any one of four bases to any one of three alternatives). Of these twelve, four are transitions, in which a purine (A,G) base replaces a purine or a pyrimidine (C,T) replaces a pyrimidine and eight are transversions in which purine is replaced by pyrimidine or vice versa. Biologically, transitions are in general much more common than transversions17. Indeed, the set of observed pathogenic mutations for our 162 genes contains 10999 transitions and 8883 transversions, whereas in the set of all mutations their ratio is by definition 1 : 2. The observed pathogenic mutations are thus already a biased selection from the set of possible mutations, favouring transitions. However, this local onsite chemical shift is not sufficient to fully explain our data as we will show later.
possible point mutations, which we denote as the set Mall, of which a subset Mpa are known pathogenic mutations. A point mutation is represented by the pair (k, s), where k is the position of the point mutation in the genomic sequence and s is the mutant nucleotide which replaces the native nucleotide. We shall write a mutation from a native base P to a mutant base Q as “Pq”. We note that there are a total of twelve possible point mutations for each nucleotide position in a DNA sequence (from any one of four bases to any one of three alternatives). Of these twelve, four are transitions, in which a purine (A,G) base replaces a purine or a pyrimidine (C,T) replaces a pyrimidine and eight are transversions in which purine is replaced by pyrimidine or vice versa. Biologically, transitions are in general much more common than transversions17. Indeed, the set of observed pathogenic mutations for our 162 genes contains 10999 transitions and 8883 transversions, whereas in the set of all mutations their ratio is by definition 1 : 2. The observed pathogenic mutations are thus already a biased selection from the set of possible mutations, favouring transitions. However, this local onsite chemical shift is not sufficient to fully explain our data as we will show later.
We compute and datamine the results of quantum mechanical transport calculations based on two effective Hückel models18 for each possible mutation in those 162 genes. The models are (i) the standard one-dimensional chain of coupled nucleic bases with onsite ionisation potentials11,15 as well as (ii) a novel 2-leg ladder model with diagonal couplings16 and explicit modelling of the sugar-phosphate backbone19,22. Both models assume π–π orbital overlap in a well-stacked double helix. The parameters are chosen to represent hole transport. Using the transfer matrix method20,21 we calculate the spatial extent of (hole) wavefunctions of a given energy on a length of DNA with a given genetic sequence. Wavefunction localisation is directly related to conductance20 and we therefore find it convenient to report our results in terms of conductance. For the specific models discussed here (for the novel 2-leg model, its precursor versions) a detailed study of the influence of the environment surrounding a DNA strand on charge migration has been presented previously22. It was shown that while the conductance results exhibited some quantitative differences, the main effect of the environment was an overall reduction which depends on the exact choice of the environment. However, such an overall effect is not a primary concern when CT changes are studied as in the present paper.
To determine the effect of a mutation, we consider sub-sequences of length L bps; there are L such sequences that include a given site k. For all L sequences we calculate quantummechanical charge transmission coefficients T (in units of  , averaged across a range of incident energies, as detailed in Methods) for the native and mutant sequences. We describe the effect of the mutation on the electronic properties of the DNA strand near to the mutation site using the mean square difference, Γ = 〈|Tnative – Tmutant|2〉, averaged across all L sequences. Larger values of Γ therefore correspond to a greater difference in electronic structure between the native and mutant sequences. The length L must be long enough to allow for substantial delocalisation across multiple base pairs22, but should remain below the typical persistence length of ∼ 150 bps23 such that any overlap or crossing by packing, e.g. by wrapping around histone complexes in chromatin, can be ignored. In this study we have considered lengths of 20, 40, 60 bps. This requires, for each of the
, averaged across a range of incident energies, as detailed in Methods) for the native and mutant sequences. We describe the effect of the mutation on the electronic properties of the DNA strand near to the mutation site using the mean square difference, Γ = 〈|Tnative – Tmutant|2〉, averaged across all L sequences. Larger values of Γ therefore correspond to a greater difference in electronic structure between the native and mutant sequences. The length L must be long enough to allow for substantial delocalisation across multiple base pairs22, but should remain below the typical persistence length of ∼ 150 bps23 such that any overlap or crossing by packing, e.g. by wrapping around histone complexes in chromatin, can be ignored. In this study we have considered lengths of 20, 40, 60 bps. This requires, for each of the  sites in a gene, L calculations for each sequence of length L and for each of 4 possible bases at that site; which, for the more than 11 × 106 bases in our dataset of 162 genes, is more than 5 × 109 quantum mechanical transport calculations.
sites in a gene, L calculations for each sequence of length L and for each of 4 possible bases at that site; which, for the more than 11 × 106 bases in our dataset of 162 genes, is more than 5 × 109 quantum mechanical transport calculations.
Local and global ranking
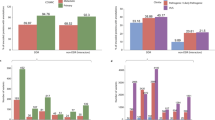
We first compare Γ of each observed pathogenic mutation with the other two non-pathogenic ones at the same position and determine a local ranking (LR) of CT change. There are three possibilities of LR, namely low, medium and high. Note that those hotspots with more than one pathogenic mutations are excluded in the LR analysis. We have also sorted the LR ranking for each gene according to prevalence in Fig. 1(a+b). We find that for L = 20, 40 and 60 the low CT change corresponds to 155 (95%), 148 (91%) and 140 (86%) of all 162 genes with pathogenic mutations. This is significantly above the 33% line expected for purely random DNA. Furthermore, the LR rankings cease their high values for low CT change upon randomly reordering the sequences. This indicates that it is indeed the fidelity of the sequence which gives rise to the observed low CT change (see examples of LR for the pathogenic mutations of p16 and CYP21A2 as well as the reordered p16 in Supplementary Fig. S3).
Sorted prevalence of the low, medium and high CT change among local (a+b) and global (c+d) rankings for pathogenic mutations in 162 genes using the 1D (a+c) and the 2-leg (b+d) models.
Results are consistent for all three lengths L = 20, 40, 60. The 1/3 value expected by chance is shown as a dashed horizontal line. Low rankings are dramatically more prevalent locally and globally than chance would suggest.
We can also consider a global ranking (GR) by sorting CT change Γ for all possible  mutations of a gene with
mutations of a gene with  bps in order to get a ranking of every observed pathogenic mutation. By dividing each ranking by
bps in order to get a ranking of every observed pathogenic mutation. By dividing each ranking by  we compute the normalised GR γ of the mutation, with values between 0 and 1. Smaller values of γ mean smaller CT change. By analogy to the local ranking, we divide the γ of the pathogenic mutations into three groups as before, i.e. low (γ < 33.3%), medium (33.3% ≤ γ < 66.7%) and high (γ ≥ 66.7%) CT change. The results of the GR for the 162 genes are shown in the bottom row (c) and (d) of Fig. 1. As for the LR results, we observe many γ values with low CT change (cp. Supplementary Figs. S3 and S4). Hence the LR and GR results consistently show that observed pathogenic mutations are generally biased towards smaller change in CT than the set of all possible mutations (cp. Supplementary Fig. S5).
we compute the normalised GR γ of the mutation, with values between 0 and 1. Smaller values of γ mean smaller CT change. By analogy to the local ranking, we divide the γ of the pathogenic mutations into three groups as before, i.e. low (γ < 33.3%), medium (33.3% ≤ γ < 66.7%) and high (γ ≥ 66.7%) CT change. The results of the GR for the 162 genes are shown in the bottom row (c) and (d) of Fig. 1. As for the LR results, we observe many γ values with low CT change (cp. Supplementary Figs. S3 and S4). Hence the LR and GR results consistently show that observed pathogenic mutations are generally biased towards smaller change in CT than the set of all possible mutations (cp. Supplementary Fig. S5).
Distributions of change in charge transport
In Figure 2 we show as an example results for the distribution of Γ for the p16 DNA strand for both 1D and 2-leg models. In panels (a+b), it is clear that the 111 observed pathogenic mutations of p16 have on average smaller changes in the CT properties as compared to all possible 80220 mutations, for both the 1D and 2-leg models. We find that results for the vast majority of the other 161 genes are quite similar. The distributions of Γ values in Fig. 2(a+b) are approximately log-normal. We therefore calculate, for each of the 162 genes in our dataset, an average log Γ value for the distributions of all and pathogenic mutations. Histograms of the distributions of these 〈log Γ〉 values are shown in Fig. 2(c+d). It is once again clear that the distributions for observed pathogenic mutations are shifted towards lower Γ values in both the 1D and the 2-leg models.
(a+b): Distribution of the change in charge transport Γ for pathogenic (orange bars) and all possible (cyan bars) mutations for the p16 (CDKN2A) gene with 26740 base pairs and 111 known pathogenic mutations. (c+d): Distribution of the average (logarithmic) change in charge transport 〈log Γ〉 for all pathogenic (orange bars) and all possible (cyan bars) mutations for all 162 genes. (e+f): Distribution of the global shift Λ values for all genes, showing a consistent tendency to positive values. The average  (dashed) and weighted average
(dashed) and weighted average  (dash-dotted) values are indicated by vertical lines similarly to the 0 line (dotted). The grey bars denote the error of mean for
(dash-dotted) values are indicated by vertical lines similarly to the 0 line (dotted). The grey bars denote the error of mean for  . The results for the 1D and 2-leg models are displayed in panels (a,c,e) and (b,d,f), respectively. All results shown are for L = 40, data for L = 20 and 60 are similar.
. The results for the 1D and 2-leg models are displayed in panels (a,c,e) and (b,d,f), respectively. All results shown are for L = 40, data for L = 20 and 60 are similar.
We next define a global CT shift for a gene g as Λg = 〈log Γg,all〉 – 〈log Γg,pa〉. Positive values of Λg indicate that the observed pathogenic mutations of gene g have a lower average Γ. For each of our 162 genes we obtain the distribution of Λg for the 1D and 2-leg models as shown in Figs. 2(e+f). We can define, for the whole set of 162 genes, an average global shift  , weighting all genes equally; we can also weight the results by the number of observed pathogenic mutations for each gene |Mpa|g for a weighted average global shift
, weighting all genes equally; we can also weight the results by the number of observed pathogenic mutations for each gene |Mpa|g for a weighted average global shift  . These values are also indicated in Figs. 2(e+f) and in both models there is a tendency towards lower average
. These values are also indicated in Figs. 2(e+f) and in both models there is a tendency towards lower average  for observed pathogenic mutations.
for observed pathogenic mutations.
Therefore the LR and GR measures, studied for a variety of system sizes and two different models for DNA, show that the pathogenic mutations found in the databases are distinguished from the set of all possible mutations by a consistently smaller change in the electronic structure as measured by Γ. In Fig. 3, we present an average over all 12 LR and GR criteria and indicate the resulting agreement with the CT hypothesis for each gene. As the figure shows, 161 of 162 genes are above the no-signal (33%) line and hence show that for both 1D and 2-leg models and averaged over lengths 20, 40 and 60, a small CT change correlates with the existence and position of pathogenic mutations.
Graphs of the average over all LR and GR criteria (cp.Fig. S5).
The red data points and gene names correspond to an alphabetic ordering of genes, whereas the blue points and labels are ordered according to the magnitude of the average. A larger average denotes a better agreement with our hypothesis. Points which lie below the dashed 33% line show genes which on average fail. Results for HSD3B2 (unsorted) and ABCA4 (sorted) have been duplicated in both rows.
Transitions and transversions
In our models we would expect transitions to cause, in general, a smaller change in CT than transversions, as the change in onsite energy and in transfer coefficients is smaller for a transition than a transversion. However, as we will demonstrate here, the increased proportion of transitions among the observed pathogenic mutations is not sufficient to account for the distributions seen in Fig. 2.
In Fig. 4(a+b) we show the distribution of Γ values for our entire dataset of all ≃ 34 × 106 possible mutations and 19882 known pathogenic mutations, dividing the datasets into transitions and transversions. For both models, the transitions are shifted to slightly lower Γ values than the transversions. However, in the 2-leg model, the distribution for observed pathogenic transitions appears co-located with the distribution for all transitions and likewise for transversions. In the 1D model, by contrast, the observed pathogenic transitions are visibly shifted to lower Γ values than the set of all transitions and the same is true for transversions.
Distributions of Γ for the 1D (a) and 2-leg (b) models for all genes, with mutations divided into transitions and transversions. The distributions are normalised by the size of the mutation dataset. Lines are guides to the eye only. The means (symbols) and standard deviations (error bars) of the distributions of log Γ are shown in panels (c) and (d) for the 1D and 2-leg models. Estimated errors of the means are smaller than the symbols. Distributions are shown for transition (Ti) and transversion (Tv) mutations and for the twelve types of point mutation individually. Open symbols (blue, cyan) are for the set of all mutations, filled symbols (orange, red) for the set of pathogenic mutations.
In Fig. 4(c+d) we represent the distributions of Γ values for each of the twelve types of point mutation by points for the mean values of log Γ and bars indicating the standard deviation of the distribution of log Γ. In the 2-leg model, the distributions for observed pathogenic mutations are essentially coincident with the distributions for all mutations for each type Pq. The positive  and
and  shift results in the 2-leg model are thus accounted for by the set of observed pathogenic mutations being biased towards transitions. The 1D model displays a quite different behaviour; in each case the mean of the distribution for the observed pathogenic mutations of any type Pq, lies from 7.5 to 20 standard errors below the mean for all possible mutations of type Pq. Hence the probability that the observed pathogenic mutations are a random subset of all mutations, with respect to their electronic properties in the 1D model, is comparable to the probability of drawing twelve values more than 7.5 standard deviations below the mean from a normal distribution, which is less than 10–168. The observed difference between CT change between observed pathogenic and all possible mutations is thus statistically highly significant irrespective of whether transitions or transversions are involved. In the 2D model, by contrast, the means of the log Γ distributions for observed pathogenic mutations can lie either above or below those for all mutations for different types Pq and the difference in the means — between 0.03 and 5.5 standard errors — is much smaller.
shift results in the 2-leg model are thus accounted for by the set of observed pathogenic mutations being biased towards transitions. The 1D model displays a quite different behaviour; in each case the mean of the distribution for the observed pathogenic mutations of any type Pq, lies from 7.5 to 20 standard errors below the mean for all possible mutations of type Pq. Hence the probability that the observed pathogenic mutations are a random subset of all mutations, with respect to their electronic properties in the 1D model, is comparable to the probability of drawing twelve values more than 7.5 standard deviations below the mean from a normal distribution, which is less than 10–168. The observed difference between CT change between observed pathogenic and all possible mutations is thus statistically highly significant irrespective of whether transitions or transversions are involved. In the 2D model, by contrast, the means of the log Γ distributions for observed pathogenic mutations can lie either above or below those for all mutations for different types Pq and the difference in the means — between 0.03 and 5.5 standard errors — is much smaller.
Let us also consider, for each gene g, simulation length L and each mutation type Pq whether the subset shift λ = 〈log Γall〉 – 〈log Γpa〉g,L,Pq is positive or negative. This gives us, for each model, 162 × 3 × 12 = 5832 data points, less 1029 cases where no calculation is possible as no pathogenic mutations of type Pq are known for gene g. These λ data are presented in Fig. 5. In the 2-leg model there are approximately equal numbers of negative and positive λ values. This is consistent with a null hypothesis where the observed pathogenic mutations of a type Pq have the same distribution of Γ vales as for all mutations of that type. In the 1D model, by contrast, such a null hypothesis is decisively rejected: there is a preponderance of positive λ values by 2.2 : 1 (3326 positive to 1513 negative) and the binomial probability of obtaining such a result at random would be approximately 10–153. The two analyses agree that observed pathogenic mutations display a significant bias towards smaller changes in electronic properties in the 1D model.
Distribution of subset shifts λ for the 2-leg (left) and 1D (right) models over all 162 genes split into the 12 possible mutations (Ac, Ag, At, Ca, … , Tc, Tg).
The capital letters on the bottom axes denote the original base pairs, whereas the lowercase letters in the top axes show the mutant base. The short red tick marks on the right axes distinguish different original bases. The system sizes L = 20, 40 and 60 are shown in the left, centre and right column for each model. The orange shading corresponds to positive λ and blue to negative. The white squares correspond to cases for which either no corresponding pathogenic mutations are known (1029 cases) or for which the subset shift is inconclusive (3 cases for the 2-leg model).
Discussion
Our CT models act as probes of the statistics of the DNA sequence. It is possible that we are merely observing a correlation; i.e. that mutations are more likely to occur in areas of the genome with certain statistical properties, for reasons not causally related to charge transport and these properties correlate with biased CT properties in our 1D model. Such a correlation between quantum transport and mutation hotspots would in itself be a valuable and novel observation in bioinformatics. There are known chemical biases in the occurence of mutations, such as the enhanced transition rate in C-G doublets24, the bias towards GC base pairs rather than AT pairs in biased gene conversion25,26 and the tendency of holes to localise on GG and GGG sequences and there cause oxidative damage27. However, since our observed bias is consistent across all twelve types of point mutation, these known biases cannot fully account for our data.
There are also plausible causal connections between our data and cellular genetic processes where the electronic properties of DNA may be significant. One such process is gene regulation, where charge transport along the DNA strand can couple to redox processes in DNA-bound proteins, inducing protein conformational change and unbinding28. Similarly, it has been proposed that DNA repair glycosylases containing redox-active [4Fe-4S] clusters29 may localise to the site of DNA lesions through a DNA-mediated charge transport mechanism30. The recognition of specific areas in the DNA sequence by DNA-binding proteins generally may involve electrostatic recognition of the target DNA sequence31. Furthermore, homologous recombination32 — a process which is vital to the repair of double-strand breaks, a most serious DNA lesion33,34 and also to genetic recombination — relies on the mutual recognition of homologous chromosomes before strand invasion can occur. Homologous double-stranded DNA sequences are capable of mutual recognition even in a protein-free environment35, presumably via electronic or electrostatic interactions36,37,38.
All the above processes, especially those involving protein–DNA or DNA–DNA recognition, would be less disrupted by a smaller change in the electronic environment along the coding strand. From this point of view, the observed mutations are biased to cause less disruption to gene regulation and DNA damage repair in the cell. This may seem counterintuitive at first. However, in order for a mutation to appear in our dataset of pathogenic mutations, the cell and the organism must develop viably for long enough for a mutant phenotype to be observed. Mutations which cause large disruptions to DNA regulation and repair are more likely to be lethal to the cell at an early stage and will thus be absent from disease databases. Similarly, mutations which are more visible to DNA repair mechanisms are less likely to persist and to appear in databases.
Genetic repair and regulation mechanisms cannot know whether the consequences of a mutation are beneficial, neutral or harmful. We would therefore predict that neutral mutations should display the same bias, towards smaller change in electronic structure, as we observe in the pathogenic mutations. As a test of this prediction, we have considered the case of the TP53 gene, with 20303 base pairs and for which there are known 2003 pathogenic mutations, 366 silent mutations and 113 intronic mutations5. We have simulated these silent and intronic mutations using the 1D model. In Table 1 we analyze the statistical properties for the resulting Γ distributions; our results demonstrate that, for both transitions and transversions, the silent and intronic mutations are similar to the pathogenic mutations and significantly disimilar to the population of all possible mutations, as predicted. For completeness, histograms of the distribution of Γ values for these mutations are given in supplementary material, see Fig. S7.
 for the silent and intronic populations is far more similar to the pathogenic populations than to the entire population of all possible mutations. This is true for both transitions and transversions, although the p-value for the intronic transitions is not statistically significant (i.e. ≥ 0.05) which we attribute to the small number of available intronic data.
for the silent and intronic populations is far more similar to the pathogenic populations than to the entire population of all possible mutations. This is true for both transitions and transversions, although the p-value for the intronic transitions is not statistically significant (i.e. ≥ 0.05) which we attribute to the small number of available intronic data.In conclusion, we have performed a large-scale data mining analysis of mutation databases and find a correlation between the occurrence of mutations and the electronic structure underlying the charge transport calculations. This correlation is novel, but not necessarily unexpected as we argue above. As ours is inherently a statistical analysis, we have not been able to elucidate the causation behind the correlation. Even so, the knowledge that the change in electronic structure induced by mutations plays a role in fundamental biological and biochemical processes hints towards the possibility of electronic prediction, early diagnosis and detection of mutation hotspots.
Methods
Models of charge transport in DNA
The simplest model of coherent hole transport in DNA is given by an effective one-dimensional Hückel-Hamiltonian for CT through nucleotide HOMO states11, where each lattice point represents a nucleotide base (A,T,C,G) of the chain for n = 1, …, N. In this tight-binding formalism, the on-site potentials εn are given by the ionisation potentials εG = 7.75eV, εC = 8.87eV, εA = 8.24eV and εT = 9.14eV, at the nth site, cp. Fig. 6; the hopping integrals tn,n+1 are assumed to be nucleotide-independent with tn,n+1 = 0.4eV11. A model which is less coarse-grained is provided by the diagonal, 2-leg ladder model shown in Fig. 6. Both strands of DNA and the backbone are modelled explicitly and the different diagonal overlaps of the larger purines (A,G) and the smaller pyrimidines (C,T) are taken into account by suitable interstrand couplings16,39. The intra-strand couplings are 0.35eV between identical bases and 0.17eV between different bases; the diagonal inter-strand couplings are 0.1eV for purine-purine, 0.01eV for purine-pyrimidine and 0.001eV for pyrimidine-pyrimidine. Perpendicular couplings to the backbone sites are 0.7eV and perpendicular hopping across the hydrogen bond in a base pair is reduced to 0.005eV. For previous discussions leading to these choices of parameters as well as the influence of the environment on the charge migration properties of the models, we refer the reader to the existing literature11,12,22. We emphasise that we have checked the robustness of our results; for example, the results for p53 do not change qualitatively when using either tn,n+1 = 0.1eV or 1eV for the 1D model.
Schematic models for charge transport in DNA.
The nucleobases are given as circles (red, denoting pairs) and ellipses (blue, brown for single nucleotides). Electronic pathways are shown as solid lines of varying thickness to indicate variation in strength. Model (a) indicates the 1D model where the sugar-phosphate backbone is ignored. In model (b), brown circles denote the smaller pyrimidines, blue ellipses are the large purines and green circles denote the sugar-phosphate backbone sites. Note that diagonal hopping between purines is favoured and between pyrimidines disfavoured, by the larger size of the purines.
The 2-leg model16 allows inter-strand coupling between the purine bases in successive base pairs, in accordance with electronic structure calculations39 and should therefore be a better model for bulk charge transport along the DNA double helix; the 1D model, by contrast, makes use of the site energies of only the bases on the coding strand15 and so is most representative of the electronic environment along that strand. We also find that the 2-leg model recovers some of the coding strand dependence of the 1D model upon decreasing the diagonal hoppings. For 28 genes, we find that reducing just the diagonal hopping elements by a factor of two leads to a much greater agreement with the 1D results similar to Fig. 4(c).
Calculation of quantum transmission coefficients
The quantum transmission coefficient T(E) for a DNA sequence with length N bps for different injection energy E can be calculated for both models by using the transfer matrix method21,40. Let us define Tj,L(E) as the transmission coefficient for a part of a given DNA sequence which starts at base pair position j and is L base pairs long. The position-dependent averaged transmission coefficient at the k–th base pair for transmission length L bps is defined as

Here j ranges from k – L + 1 to k such that each subsequence of length L contains the kth base pair. E0 and E1 are the lower and upper bounds of the incident energy of the carriers, e.g. for the 1D model used here, the values are 5.75 and 9.75eV, respectively; for the 2-leg model the bounds are 7 and 11eV. We have used an energy resolution of ΔE = 0.005eV. Then we examine the difference between transmission coefficients of the normal and mutated genomic sequence of a point mutation15 and hence denote by  the transmission coefficient of the same segment of DNA as
the transmission coefficient of the same segment of DNA as  but with the point mutation (k, s).
but with the point mutation (k, s).  is the averaged effect of the point mutation (k, s) on CT properties for all subsequences of length L containing the mutation,
is the averaged effect of the point mutation (k, s) on CT properties for all subsequences of length L containing the mutation,

References
Sherbet, G. V. Genetic Recombination in Cancer (Academic Press, 2003).
Frank, S. A. Dynamics of Cancer: Incidence, Inheritance and Evolution. Princeton Series in Evolutionary Biology (Princeton University Press, Princeton and Oxford, 2007).
McKusick-Nathans Institute of Genetic Medicine. Online Mendelian inheritance in man (2010). URL http://www.ncbi.nlm.nih.gov/omim/. Johns Hopkins University (Baltimore, MD) and National Center for Biotechnology Information, National Library of Medicine (Bethesda, MD).
Steson, P. D. et al. Human gene mutation database (HGMD): 2003 update. Hum. Mutat. 21, 577–581 (2003). URL http://www.hgmd.cf.ac.uk/ac/index.php.
Petitjean, A. et al. Impact of mutant p53 functional properties on TP53 mutation patterns and tumor phenotype: lessons from recent developments in the IARC TP53 database. Hum. Mutat. 28, 622–29 (2007). Http://www-p53.iarc.fr/index.html, R11.
Lohmann, D. R. & Gallie, B. A. L. Retinoblastoma: Revisiting the model prototype of inherited cancer. Am. J. Med. Genet. C 129C, 23–28 (2005). http://www.verandi.de/joomla.
Nagl, S. (ed.) Cancer Bioinformatics (Wiley, Chichester, England., 2006).
Enkemann, S. A., McLoughlin, J. M., Jensen, E. H. & Yeatman, T. J. Whole-genome analysis of cancer. In: Gordon G. J. (ed.) Cancer Drug Discovery and Development, chap. 3, 25–55 (Humana Press, 2009).
The International Cancer Genome Consortium. International network of cancer genome projects. Nature 464, 993–998 (2010).
Starikov, E. B., Lewis, J. P., & Tanaka, S. (eds.) Modern Methods for Theoretical Physical Chemistry of Biopolymers (Elsevier, Amsterdam, 2006).
Chakraborty, T. (ed.) Charge Migration in DNA: Perspectives from Physics, Chemistry and Biology (Springer Verlag, Berlin, 2007).
Berashevich, J. & Chakraborty, T. Mutational hot spots in DNA: where biology meets physics. Physics in Canada 63, 103–107 (2007).
Genereux, J., Boal, A. & Barton, J. DNA-mediated charge transport in redox sensing and signalling. J. Am. Chem. Soc. 132, 891–905 (2010).
Guo, X., Gorodetsky, A. A., Hone, J., Barton, J. K. & Nuckolls, C. Conductivity of a single DNA duplex bridging a carbon nanotube gap. Nature Nanotechnology 3, 163 (2008).
Shih, C. -T., Roche, S. & Römer, R. A. Point-mutation effects on charge-transport properties of the tumor-suppressor gene p53. Phys. Rev. Lett. 100, 018105 (2008).
Wells, S. A., Shih, C. -T. & Römer, R. A. Modelling charge transport in DNA using transfer matrices with diagonal terms. Int. J. Mod. Phys. B 23, 4138–4149 (2009).
Collins, D. & Jukes, T. Rates of transition and transversion in coding sequences since the human-rodent divergence. Genomics 20, 386–396 (1994).
Powell, B. J. Computational Methods for Large Systems: Electronic Structure Approaches for Biotechnology and Nanotechnology, chap. An introduction to effective low-energy Hamiltonians in condensed matter physics and chemistry (Wiley, Hoboken, 2011).
Cuniberti, G., Craco, L., Porath, D. & Dekker, C. Backbone-induced semiconducting behavior in short DNA wires. Phys. Rev. B 65, 241314(R)–4 (2002).
Kramer, B. & MacKinnon, A. Localization: theory and experiment. Rep. Prog. Phys. 56, 1469–1564 (1993).
Ndawana, M. L., Römer, R. A. & Schreiber, M. Effects of scale-free disorder on the Anderson metal-insulator transition. Europhys. Lett. 68, 678–684 (2004).
Klotsa, D. K., Römer, R. A. & Turner, M. S. Electronic transport in DNA. Biophys. J. 89, 2187–2198 (2005).
Hegerman, P. J. Flexibility of DNA. Ann. Rev. Biophys. Biophys. Chem 17, 265–286 (1988).
Blake, R., Hess, S. & Nicholson-Tuell, J. The influence of nearesst neighbors on the rate and pattern of spontaneous point mutations. J Mol Evol 34, 189–200 (1992).
Galtier, N. & Duret, L. Adaptation of biased gene conversion? extending the null hypothesis of molecular evolution. TRENDS in Genetics 23, 273–277 (2007).
Marais, G. Biased gene conversion; implications for genome and sex evolution. TRENDS in Genetics 19, 330–338 (2003).
Nunez, M., Holmquist, G. & Barton, J. Evidence for DNA charge transport in the nucleus. Biochemistry 40, 12465–12471 (2001).
Augustyn, K. E., Merino, E. J. & Barton, J. K. A role for DNA-mediated charge transport in regulating p53: Oxidation of the DNA-bound protein from a distance. Proc. Nat. Acad. Sci. 104, 18907–18912 (2007).
Boal, A., Yavin, E. & Barton, J. DNA repair glycosylases with a [4fe-4s] cluster: a redox cofactor for DNA-mediated charge transport? J. Inorg. Biochem. 101, 1913–1921 (2007).
Yavin, E., Stemp, E. D. A., O'Shea, V. L., David, S. S. & Barton, J. K. Electron trap for DNA-bound repair enzymes: A strategy for DNA-mediated signaling. Proc. Nat. Acad. Sci. 103, 3610 (2006).
Cherstvy, A., Kolomeisky, A. & Kornyshev, A. Protein-DNA interactions; reaching and recognizing the targets. J. Phys. Chem. B 112, 4741–4750 (2008).
Ferguson, D. & Alt, F. DNA double strand break repair and chromosomal translocation: lessons from animal models. Oncogene 20, 5572–5579 (2001).
Jackson, S. Sensing and repairing DNA double-strand breaks- commentary. Carcinogenesis 23, 687–696 (2002).
Khanna, K. & Jackson, S. DNA double-strand breaks: signalling, repair and the cancer connection. Nature Genetics 27, 247–254 (2001).
Baldwin, G. S. et al. DNA double helices recognize mutual sequence homology in a protein free environment. J. Phys. Chem. B 114, 1060–1064 (2008).
Kornyshev, A. A. & Leikin, S. Sequence recognition in the pairing of DNA duplexes. Phys. Rev. Lett. 86, 3666–3669 (2001).
Cherstvy, A. Positively charged residues in DNA-binding domains of structural proteins follow sequence-specific positions of DNA phosphate groups. J. Phys. Chem. B 113, 4242–4247 (2009).
Cherstvy, A. DNA-DNA sequence homology recognition: physical mechanisms and open questions. J. Mol. Recognit. 24, 283–287 (2010).
Rak, J., Voityuk, A., Marquez, A. & Rösch, N. The effect of pyrimidine bases on the holetransfer coupling in DNA. J. Phys. Chem. B 106, 7919–7926 (2002).
Roche, S. Sequence dependent DNA-mediated conduction. Phys. Rev. Lett. 91, 108101–4 (2003).
Acknowledgements
This work was supported by the National Science Council in Taiwan (CTS, Grant No. 97-2112-M-029-002-MY3 and 100-2112-M-029-001-MY3) and the UK Leverhulme Trust (RAR, SAW, Grant No. F/00215/AH). Part of the calculations were performed at the National Center for High-Performance Computing in Taiwan. We are grateful for their help.
Author information
Authors and Affiliations
Contributions
CTS and RAR coordinated the international collaboration and wrote the main manuscript text. CTS, RAR and SAW wrote the programs and performed the main computation. YYC and CLH analyzed the source databases and performed the data preprocessing. All authors analyzed the data and reviewed the manuscript.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Electronic supplementary material
Supplementary Information
Supplementary information
Rights and permissions
This work is licensed under a Creative Commons Attribution-NonCommercial-ShareALike 3.0 Unported License. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-sa/3.0/
About this article
Cite this article
Shih, CT., Wells, S., Hsu, CL. et al. The interplay of mutations and electronic properties in disease-related genes. Sci Rep 2, 272 (2012). https://doi.org/10.1038/srep00272
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep00272
This article is cited by
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.