Abstract
Many social, biological and technological networks consist of a small number of highly connected components (hubs) and a very large number of loosely connected components (low-degree nodes). It has been commonly recognized that such heterogeneously connected networks are extremely vulnerable to the failure of hubs in terms of structural robustness of complex networks. However, little is known about dynamical robustness, which refers to the ability of a network to maintain its dynamical activity against local perturbations. Here we demonstrate that, in contrast to the structural fragility, the nonlinear dynamics of heterogeneously connected networks can be highly vulnerable to the failure of low-degree nodes. The crucial role of low-degree nodes results from dynamical processes where normal (active) units compensate for the failure of neighboring (inactive) units at the expense of a reduction in their own activity. Our finding highlights the significant difference between structural and dynamical robustness in complex networks.
Similar content being viewed by others
Introduction
Network science has witnessed many developments in the last decade because many real-world networks were found to have a variety of topological structures1,2,3. The complexity of a network structure can be characterized by the connectivity properties of the interaction pathways (links) between network components (nodes). The degree of a node is the number of its links connected to other nodes. In terms of the degree distribution (the probability distribution of the degrees of all the nodes in the network), complex networks can be classified into homogeneous and heterogeneous networks. Homogeneous networks such as random graphs4 and small-world models5 possess binomial or Poisson degree distribution, where the degrees concentrate around the mean degree. Heterogeneous networks such as scale-free networks6 have a heavy-tailed degree distribution that at least approximately follows a power law. Data analyses have revealed that the scale-free property is found in social7,8, biological9,10,11, technological12,13 and many other types of networks1,2,3,6.
One of the major characteristics of heterogeneous networks is that they are highly robust against random errors but are extremely fragile to attacks targeted at hubs14. Namely, the connectivity properties of a heterogeneous network as a whole are not so much affected by the random removal of a fraction of the nodes as compared with a homogeneous network; however, they are drastically altered by the preferential removal of hubs, leading to network fragmentation. These properties have been theoretically studied by means of percolation theory15,16,17. The structural fragility to the preferential removal of important nodes is also observed in heterogeneous network models incorporating dynamical flows of physical quantities on the network18,19,20. Most of these studies are concerned with the robustness of the network structure: the measure of network function is given by the size of the giant component (the largest connected subnetwork) and failure nodes are removed to induce a topological change. However, less attention has been paid to changes in network dynamics caused by local errors in complex networks of dynamical units20, which are particularly relevant to biological robustness21,22. Because most real-world complex networks are composed of elements with internal dynamics, it is essential to consider the robustness with respect to nonlinear dynamics.
Here we focus on the dynamical robustness of complex networks, which is defined as the ability of a network to maintain its dynamical activity when a fraction of the dynamical components are deteriorated or functionally depressed but not removed. Our aim is to demonstrate that the key nodes impacting the dynamical robustness of heterogeneous networks are low-degree nodes. This is in strong contrast to the structural robustness which is largely influenced by hubs. As an example of networks consisting of dynamical units, we introduce coupled oscillator networks23,24,25 which have often been used to study a variety of biological phenomena including circadian rhythms, synchronized neuronal firing and spatiotemporal activity in the heart and the brain. In the mammalian suprachiasmatic nucleus (SCN) producing a biological clock that drives circadian rhythms, normal function is sustained by networks of SCN neuronal oscillators26. The self-sustained oscillation of each individual SCN neuron can be damped because of some environmental conditions27 or age-related deterioration28. Coupled oscillator models are useful for exploring how circadian rhythms are robustly generated in a population of self-sustained and damped circadian oscillators29. In the pancreatic islets, synchronized oscillatory activity of electrically coupled beta cells is involved in pulsatile insulin secretion that regulates blood glucose levels. A major issue that has been studied using coupled oscillator models is how rhythmic insulin secretion can be robustly achieved in populations of heterogeneous cells that are active or silent30. There are many other dynamical cellular and multicellular processes in which oscillation plays important roles31,32. Moreover, coupled oscillator models are also relevant to electric power networks in which network components like power sources should be synchronized at the same frequency33. It is essential to investigate how the collective dynamics of power networks is tolerant to local disturbances of power sources that may lead to a cascading blackout34,35.
We consider networks consisting of N oscillator nodes coupled by diffusive connections with fixed strength K (see Methods section). A normal (active) oscillator exhibits periodic oscillation when it is isolated, whereas a deteriorated (inactive) oscillator settles down in a quiescent state after transient damping oscillation (Fig. 1a)36,37. Unless any local deterioration occurs, the network of all active oscillators produces completely synchronized oscillation. When a proportion of the oscillators are randomly inactivated with ratio p in a heterogeneous network (Fig. 1b), we observe phase synchronized oscillation with different amplitudes (Fig. 1c). The individual inactive oscillator, which cannot oscillate by itself, manages to continue weak oscillation in the network because of continuous inputs from neighboring active oscillators through diffusive coupling. Instead, the active oscillators decrease their oscillation levels as compared with the isolated ones in order to achieve a balance between their states and those of neighboring inactive oscillators.
An oscillator network model.
(a) The behavior of the isolated active (red curve) and inactive (blue curve) oscillators. The active oscillator exhibits periodic oscillation, whereas the inactive oscillator becomes quiescent after transient damping oscillation. (b) A heterogeneous network composed of active (red nodes) and inactive (blue nodes) oscillators. Here, the oscillators are randomly inactivated with ratio p = 0.3. The link density is d ∼ 0.08 (N = 100 and 〈k〉 = 8). (c) The behavior of (1 − p)N active (red curves) and pN inactive oscillators (blue curves) in the network. The coupling strength is set at K = 30. The solid black curve in each panel indicates the mean field for each subpopulation. The inactive oscillators, which are not able to oscillate when isolated, manage to sustain the oscillatory behavior because of the diffusive interactions with neighboring active oscillators. All the oscillators show phase synchronization.
Results
Behavior in the oscillator network model
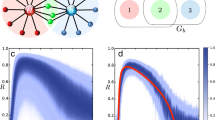
The oscillation amplitude of a node is largely dependent on the degree of the node in heterogeneous networks (Fig. 2a), as compared with homogeneous networks (Fig. 2c). When a part of the oscillators are randomly inactivated independently of their degrees, the expected number of inactive oscillators connected to a node is proportional to the degree of the node. Therefore, within the subpopulation of active oscillators, the nodes with lower degree are likely to generate larger oscillation amplitudes because they are less affected by the neighboring inactive oscillators. To measure the network activity, we introduce the order parameter |Z| that represents the average of the oscillation amplitudes over all the oscillators in the phase synchronization state (see Methods section). As the ratio p increases, the order parameter decreases (Figs. 2b and 2d). When p exceeds a critical value pc, the order parameter vanishes with a loss of global oscillation. For a sufficiently large coupling strength K, the order parameter displays a second-order phase transition at p = pc36,37. The critical ratio pc, namely the maximum inactivation ratio for which the network activity is sustainable, is regarded as a measure of the dynamical robustness. A higher critical value implies a more dynamically robust network.
Behavior in heterogeneous and homogeneous networks.
(a), (c) The upper panel shows the degrees kj of individual oscillators in (a) heterogeneous and (c) homogeneous networks with d ∼ 0.08 (N = 1,000 and 〈k〉 = 80), K = 30 and p = 0.55. The lower panel shows the oscillation amplitudes |zj| of the individual oscillators. (b), (d) The order parameter |Z| is plotted against the inactivation ratio p for (b) heterogeneous and (d) homogeneous networks with d ∼ 0.08 (N = 1,000 and 〈k〉 = 80). The critical ratio pc, at which |Z| reaches 0, is different between the two types of networks for sufficiently large K. The error bars indicating the variance for 10 network realizations are invisibly small.
Random inactivation
In the case where oscillators are randomly inactivated, the critical ratio pc is analytically obtained for both heterogeneous and homogeneous networks (see Methods section and Supplementary Information). The degree of the jth oscillator is denoted by kj (j = 1, …, N) and the mean degree, by  . We assume that the behavior of a heterogeneous network with large N is governed by two mean fields corresponding to the subpopulations of active and inactive oscillators. In order to apply the degree-weighted mean field approximation38,39 or the annealed network approximation40 to each subnetwork, we assume that the oscillators with the same degree in the same subpopulation are identical. Under this assumption, the critical ratio pc for heterogeneous networks is derived as follows:
. We assume that the behavior of a heterogeneous network with large N is governed by two mean fields corresponding to the subpopulations of active and inactive oscillators. In order to apply the degree-weighted mean field approximation38,39 or the annealed network approximation40 to each subnetwork, we assume that the oscillators with the same degree in the same subpopulation are identical. Under this assumption, the critical ratio pc for heterogeneous networks is derived as follows:

where d ≡ 〈k〉/(N − 1) (∼ 〈k〉/N for large N) is the link density, K is the coupling strength and a > 0 and −b < 0 are the values of the intrinsic parameters for the active and inactive oscillators, respectively (see Methods section). The function F is dependent on the degree distribution normalized by the system size as well as the coupling strength and the intrinsic parameters (see equation (6)). The critical coupling strength, below which  , is given by
, is given by  , where dmin ≡ kmin/N with the minimum degree kmin ≡ min1≤j≤Nkj. For homogeneous networks, we further assume that the degrees of all the oscillators are approximated by the mean degree for analytical calculations. Then, the critical ratio is described as follows:
, where dmin ≡ kmin/N with the minimum degree kmin ≡ min1≤j≤Nkj. For homogeneous networks, we further assume that the degrees of all the oscillators are approximated by the mean degree for analytical calculations. Then, the critical ratio is described as follows:

where  . The critical ratio is invariant if the product of the link density and the coupling strength is kept constant. Hence, a more strongly or densely connected network is less robust. The critical ratios for homogeneous and heterogeneous networks are plotted against the coupling strength K and the link density d in Figs. 3a and 3b. The results of the analytical formulae are in good agreement with the corresponding numerical results. For a wide range of parameter values, the critical ratio for the heterogeneous network is larger than that for the homogeneous network. This property can be further confirmed by the comparison between Fig. 4a for heterogeneous networks and Fig. 4b for homogeneous networks in the parameter space of K and d. Therefore, heterogeneous networks are more tolerant to random inactivation than homogeneous ones. This result is consistent with that based on the structural robustness against random removal of nodes1,2,3,14,15,16,17.
. The critical ratio is invariant if the product of the link density and the coupling strength is kept constant. Hence, a more strongly or densely connected network is less robust. The critical ratios for homogeneous and heterogeneous networks are plotted against the coupling strength K and the link density d in Figs. 3a and 3b. The results of the analytical formulae are in good agreement with the corresponding numerical results. For a wide range of parameter values, the critical ratio for the heterogeneous network is larger than that for the homogeneous network. This property can be further confirmed by the comparison between Fig. 4a for heterogeneous networks and Fig. 4b for homogeneous networks in the parameter space of K and d. Therefore, heterogeneous networks are more tolerant to random inactivation than homogeneous ones. This result is consistent with that based on the structural robustness against random removal of nodes1,2,3,14,15,16,17.
Comparison of the critical ratio with respect to coupling strength K and link density d between heterogeneous and homogeneous networks for random inactivation.
(a) The critical ratio pc is plotted against the coupling strength K in networks with d ∼ 0.08 (N = 3000 and 〈k〉 = 240). A globally oscillatory state with |Z| > 0 is observed for p < pc, whereas a quiescent state with |Z| = 0 is observed for p > pc. The solid and dashed black curves indicate the analytically obtained results in equations (1) and (2), respectively. Blue diamonds and red triangles indicate the numerically obtained results. The error bars indicate the variance for 10 network realizations. (b) The critical ratio pc is plotted against the link density d in networks with N = 3000 and K = 30.
Dependence of the critical ratio on coupling strength K and link density d.
The color indicates the value of the critical ratio pc in networks with N = 3000. (a) Heterogeneous networks for random inactivation. (b) Homogeneous networks for random inactivation. (c) Heterogeneous networks for targeted inactivation of low-degree nodes. (d) Heterogeneous networks for targeted inactivation of high-degree nodes.
Targeted inactivation
In the case where oscillators are not randomly inactivated, the mean field approximation is not appropriate. Thus, we numerically computed the critical ratios for preferential inactivation targeted at either high-degree or low-degree nodes in heterogeneous networks. First, the node with the highest (lowest) degree among the active oscillators was inactivated. Then, this process was repeated until the number of inactive oscillators became pN. The critical ratio for targeted inactivation is compared with that for random inactivation in heterogeneous networks, as shown in Figs. 5a and 5b. Compared with the random inactivation case, the targeted inactivation of low-degree nodes makes the networks significantly vulnerable for a wide range of parameter values. This consequence is opposite to the structural fragility against removal of hubs. Figures 4a and 4c also clearly show the difference between the critical ratio pc for random inactivation and that for targeted inactivation of low-degree nodes. As explained before, the active oscillators with lower degrees are likely to exhibit larger oscillation amplitudes (see Fig. 2a). Therefore, the inactivation of low-degree nodes more dramatically decreases the order parameter and thereby results in a lower critical ratio compared with the random inactivation. The critical coupling strength indicated in Fig. 5a is obtained as  , where dmax ≡ kmax/N with the maximum degree kmax ≡ max1≤j≤Nkj. The critical coupling strength is considerably decreased by the inactivation of low-degree nodes, i.e.
, where dmax ≡ kmax/N with the maximum degree kmax ≡ max1≤j≤Nkj. The critical coupling strength is considerably decreased by the inactivation of low-degree nodes, i.e.  . On the other hand, the inactivation of the high-degree nodes (hubs) makes heterogeneous networks slightly more robust as compared with the random inactivation. This is because active oscillators with higher degree contribute less to the order parameter (see Fig. 2a). In this case, the critical coupling strength indicated in Fig. 5a is given by
. On the other hand, the inactivation of the high-degree nodes (hubs) makes heterogeneous networks slightly more robust as compared with the random inactivation. This is because active oscillators with higher degree contribute less to the order parameter (see Fig. 2a). In this case, the critical coupling strength indicated in Fig. 5a is given by  . The difference between the critical ratio pc for random inactivation and that for targeted inactivation of high-degree nodes is subtle, as shown in Figs. 4a and 4d.
. The difference between the critical ratio pc for random inactivation and that for targeted inactivation of high-degree nodes is subtle, as shown in Figs. 4a and 4d.
Comparison of the critical ratio with respect to coupling strength K and link density d between random and targeted inactivation in heterogeneous networks.
(a) The critical ratio pc is plotted against the coupling strength K in heterogeneous networks with d ∼ 0.08 (N = 3000 and 〈k〉 = 240), dmax ∼ 0.3 and dmin ∼ 0.04. Blue diamonds and the black solid curve indicate the numerically and theoretically obtained critical ratios for random inactivation, respectively. Green circles and pink squares indicate the critical ratios for the targeted inactivation of low-degree and high-degree nodes, respectively. The critical coupling strength is given by  for the former case and
for the former case and  for the latter case, as theoretically predicted. (b) The critical ratio pc is plotted against the link density d in heterogeneous networks with N = 3000 and K = 30.
for the latter case, as theoretically predicted. (b) The critical ratio pc is plotted against the link density d in heterogeneous networks with N = 3000 and K = 30.
Discussion
We have demonstrated that heterogeneous networks are highly tolerant to random inactivation but extremely fragile to targeted inactivation of low-degree oscillators with respect to the dynamical robustness. The former property is consistent with the structural robustness of heterogeneous networks14. The latter property sheds light on the critical difference between the structural robustness and the dynamical robustness. These properties also hold for coupled oscillator models in which the coupling strengths are not identical but uniformly or normally distributed (see Supplementary Information). Our finding results from the diffusive coupling that serves to balance the states of the two connected nodes. Active nodes function to restore neighboring inactive nodes, with a resulting weakening of their dynamical activity. Because low-degree active nodes are affected by only a few neighboring inactive nodes, they can maintain relatively high dynamical activity compared with high-degree active nodes. Therefore, targeted inactivation of low-degree nodes leads to a considerable reduction in the network dynamical activity, making the network dynamically vulnerable.
This mechanism is expected to be applicable to a wide range of networked systems, because diffusion in various transport phenomena are commonly found in physical, biological and engineering systems. For example, electrical synapses or gap junctions that are widely observed in the brain41 can be modeled by diffusive coupling in neural networks42; in particular, rhythmicity and synchrony among inferior olive neurons43 can be quantitatively described by a neural network model composed of oscillatory neurons coupled through such electrical synapses44. Electric power networks that are composed of distributed power sources including renewable energy sources with inverters45,46 such as wind and solar power can also be modeled as a coupled oscillator network33 interconnected by diffusive coupling with active and reactive power flows.
Our results imply that dynamical processes play an important role in understanding the dynamical robustness in complex networks composed of interacting dynamical units. One needs to appropriately model dynamical processes and define a measure of dynamicsbased network function to mathematically treat the dynamical robustness in such realworld networks as biological cellular networks11,21, metabolic networks9, protein networks10, brain networks47 and electric power networks48. For designing dynamically robust networks and planning recovery strategies against local errors, both the network structure and the dynamical processes should be considered in detail.
Methods
Model equations
The network of diffusively coupled oscillators is described as follows:

where N is the number of oscillators; zj, the complex state variable of the jth oscillator; αj, the intrinsic parameter of the jth oscillator; Ω, the natural frequency; and K, the coupling strength. The single oscillator without coupling (K = 0), called the Stuart-Landau oscillator24, represents the normal form of dynamical systems that describe the nonlinear dynamics near the supercritical Hopf bifurcation at αj = 049. The single oscillator exhibits periodic (active) oscillation for a positive value of αj, whereas it becomes quiescent (inactive) for a negative value of αj (see Fig. 1a). The set of node indices for the active oscillators is denoted by SA and that for the inactive oscillators, by SI. We set αj = a > 0 for j ∈ SA and αj = −b < 0 for j ∈ SI36,37. The parameter values are fixed at a = 1, b = 3 and Ω = 3. The adjacency matrix A = (Ajk) represents the network connectivity, where Ajk = Akj = 1 if the jth and the kth oscillators are connected and Ajk = Akj = 0 otherwise. The degree of the jth oscillator is given by  . The homogeneous and heterogeneous networks are given by the Erdös-Rényi random graph4 and the Barabási-Albert scale-free model6, respectively.
. The homogeneous and heterogeneous networks are given by the Erdös-Rényi random graph4 and the Barabási-Albert scale-free model6, respectively.
Order parameter and critical ratio
The macroscopic oscillation level of the entire network is evaluated by the order parameter |Z|, where  . When all the oscillators stop oscillating, the order parameter vanishes. As the ratio p of inactive oscillators increases from zero, the order parameter decreases and vanishes at a critical ratio p = pc (see Figs. 2b and 2d). In simulation experiments, the model equation (3) with random initial conditions was numerically integrated by the fourth-order Runge-Kutta method with time step 0.1 and the order parameter |Z| was calculated at t = 50000. We considered the critical value pc to be the value of p at which the value of |Z| at t = 50000 falls below 10−6 as p is increased.
. When all the oscillators stop oscillating, the order parameter vanishes. As the ratio p of inactive oscillators increases from zero, the order parameter decreases and vanishes at a critical ratio p = pc (see Figs. 2b and 2d). In simulation experiments, the model equation (3) with random initial conditions was numerically integrated by the fourth-order Runge-Kutta method with time step 0.1 and the order parameter |Z| was calculated at t = 50000. We considered the critical value pc to be the value of p at which the value of |Z| at t = 50000 falls below 10−6 as p is increased.
Mean field approximation
The critical ratio for random inactivation is analytically obtained by the mean field approximation38,39 or the annealed network approximation40. The sum of contributions to the jth oscillator from the connected oscillators in Eq. (3) is represented by the local field  . For sufficiently large N, the number of active oscillators in the neighborhood of the jth oscillator is expected to be (1 − p)kj and that of inactive ones, pkj. Therefore, based on numerical observations (see Supplementary Information), we approximate the local field as follows:
. For sufficiently large N, the number of active oscillators in the neighborhood of the jth oscillator is expected to be (1 − p)kj and that of inactive ones, pkj. Therefore, based on numerical observations (see Supplementary Information), we approximate the local field as follows:

where the degree-weighted mean fields HA(t) and HI(t) for active and inactive subpopulations are given by

Accordingly, the original equation (3) can be approximated as follows:

The coupling term, which is dependent on the connectivity matrix Ajk in the original equation, is now only dependent on the degree of the node. Once the mean fields HA and HI are provided, the steady oscillatory state of the jth oscillator is obtained from the reduced form (5). For the mean field approximation to be self-consistent, the mean fields calculated by equation (4) from the steady oscillatory states must be equivalent to the originally given mean fields. From a self-consistency analysis (see Supplementary Information), we derive the critical ratio (1) with

where dj = kj/N is the degree of the jth oscillator, normalized by the system size.
For homogeneous networks, we further assume that the degrees of all the oscillators are the same as the mean degree, i.e. kj = 〈k〉 = (1/N)Σjkj for all j. Then, because dj = d = 〈k〉/N for all j, equation (6) is reduced to F(K, α) = d2/(d−α/K). By substituting this form into equation (1), we obtain equation (2). See Supplementary Information for further details.
References
Albert, R. & Barabási, A.-L. Statistical mechanics of complex networks. Rev. Mod. Phys. 74, 1, 47–97 (2002).
Newman, M. E. J. The structure and function of complex networks. SIAM Review 45, 167–256 (2003).
Boccaletti, S., Latora, V., Moreno, Y., Chavez, M. & Hwang, D.-U. Complex networks: structure and dynamics. Phys. Rep. 424, 175–308 (2006).
Erdös, P. & Rényi, A. On the evolution of random graphs. Publications of the Mathematical Institute of the Hungarian Academy of Sciences 5, 17–61 (1960).
Watts, D. J. & Strogatz, S. H. Collective dynamics of ‘small-world’ networks. Nature 393, 440–442 (1998).
Barabási, A. L. & Albert, R. Emergence of scaling in random networks. Science 286, 5439, 509–512 (1999).
Redner, S. How popular is your paper? An empirical study of the citation distribution. Euro. Phys. J. B 4, 131–134 (1998).
Liljeros, F., Edling, C. R., Amaral, L. A. N., Stanley, H. E. & Aberg, Y. The web of human sexual contacts. Nature 411, 907–908 (2001).
Jeong, H., Tombor, B., Albert, R., Oltvai, Z. N. & Barabási, A.-L. The large-scale organization of metabolic networks. Nature 407, 651–654 (2000).
Jeong, H., Mason, S., Barabási, A. L. & Oltvai, Z. N. Lethality and centrality in protein networks. Nature 411, 41–42 (2001).
Albert, R. Scale-free networks in cell biology. J. Cell Sci. 118, 4947–4957 (2005).
Albert, R., Jeong, H. & Barabási, A.-L. Diameter of the world wide web. Nature 401, 130–131 (1999).
Pastor-Satorras, R. & Vespignani, A. Evolution and Structure of the Internet. (Cambridge University Press, 2004).
Albert, R., Jeong, H. & Barabási, A.-L. Error and attack tolerance of complex networks. Nature 406, 378–382 (2000).
Callaway, D. S., Newman, M. E. J., Strogatz, S. H. & Watts, D. J. Network robustness and fragility: percolation on random graphs. Phys. Rev. Lett. 85, 25, 5468–5471 (2000).
Cohen, R., Erez, K., ben Avraham, D. & Havlin, S. Resilience of the Internet to random breakdowns. Phys. Rev. Lett. 85, 21, 4626–4628 (2000).
Cohen, R., Erez, K., ben Avraham, D. & Havlin, S. Breakdown of the Internet under intentional attack. Phys. Rev. Lett. 86, 16, 3682–3685 (2001).
Watts, D. J. A simple model of global cascades on random networks. Proc. Natl. Acad. Sci. USA 99, 9, 5766–5771 (2002).
Motter, A. E. & Lai, Y.-C. Cascade-based attacks on complex networks. Phys. Rev. E 66, 065102(R) (2002).
Wang, X. F. & Xu, J. Cascading failures in coupled map lattices. Phys. Rev. E 70, 056113 (2004).
Barabási, A.-L. & Oltvai, Z. N. Network biology: understanding the cell's functional organization. Nature Rev. Genet. 5, 101–113 (2004).
Kitano, H. Biological robustness. Nature Rev. Genet. 5, 826–837 (2004).
Winfree, A. T. The Geometry of Biological Time. (Springer, New York, 1980).
Kuramoto, Y. Chemical Oscillations, Waves and Turbulence. (Springer-Verlag, 1984).
Strogatz, S. Exploring complex networks. Nature 410, 268–276 (2001).
Welsh, D. K., Takahashi, J. S. & Kay, S. A. Suprachiasmatic nucleus: cell autonomy and network properties. Annu. Rev. Physiol. 72, 551–577 (2010).
Webb, A. B., Angelo, N., Huettner, J. E. & Herzog, E. D. Intrinsic, nondeterministic circadian rhythm generation in identified mammalian neurons. Proc. Natl. Acad. Sci. USA 106, 38, 16493–16498 (2009).
Aujard, F., Herzog, E. D. & Block, G. D. Circadian rhythms in firing rate of individual suprachi-asmatic nucleus neurons from adult and middle-aged mice. Neuroscience 106, 2, 255–261 (2001).
Bernard, S., Gonze, D., Čajavec, B., Herzel, H. & Kramer, A. Synchronization-induced rhythmicity of circadian oscillators in the suprachiasmatic nucleus. PLoS Comput. Biol. 3, 4, 667–679 (2007).
Smolen, P., Rinzel, J. & Sherman, A. Why pancreatic islets burst but single β cells do not. Biophys. J. 64, 1668–1680 (1993).
Kruse, K. & Jülicher, F. Oscillations in cell biology. Curr. Opin. Cell Biol. 17, 20–26 (2005).
Chen, L., Wang, R., Li, C. & Aihara, K. Modeling Biomolecular Networks in Cells: Structures and Dynamics. (Springer-Verlag, 2010).
Filatrella, G., Nielsen, A. H. & Pedersen, N. F. Analysis of a power grid using a Kuramoto-like model. Eur. Phys. J. B 61, 485–491 (2008).
Gellings, C. W. & Yeager, K. E. Transforming the electric infrastructure. Phys. Today 57, 12, 45–51 (2004).
Fairley, P. The unruly power grid. IEEE Spectrum 41, 8, 22–27 (2004).
Daido, H. & Nakanishi, K. Aging transition and universal scaling in oscillator networks. Phys. Rev. Lett. 93, 10, 104101 (2004).
Morino, K., Tanaka, G. & Aihara, K. Robustness of multilayer oscillator networks. Phys. Rev. E 83, 056208 (2011).
Pastor-Satorras, R. & Vespignani, A. Epidemic spreading in scale-free networks. Phys. Rev. Lett. 86, 14, 3200–3203 (2001).
Nakao, H. & Mikhailov, A. S. Turing patterns in network-organized activator-inhibitor systems. Nature Phys. 6, 544–550 (2010).
Dorogovtsev, S. N., Goltsev, A. V. & Mendes, J. F. F. Critical phenomena in complex networks. Rev. Mod. Phys. 80, 4, 1275–1335 (2008).
Galarreta, M. & Hestrin, S. Electrical synapses between GABA-releasing interneurons. Nat. Rev. Neurosci. 2, 425–433 (2001).
Aihara, K. & Tokuda, I. Possible neural coding with interevent intervals of synchronous firing. Phys. Rev. E 66, 026212 (2002).
Lang, E. J, Sugihara, I. & Llinás, R. GABAergic modulation of complex spike activity by the cerebellar nucleoolivary pathway in rat. J. Neurophysiol. 76, 1, 255–275 (1996).
Katori, Y., Lang, E. J., Onizuka, M., Kawato, M. & Aihara, K. Quantitative modeling of spatiotemporal dynamics of inferior olive neurons with a simple conductance-based model. Int. J. Bifurcat. Chaos 20, 3, 583–603 (2010).
Blaabjerg, F., Teodorescu, R., Liserre, M. & Timbus, A. V. Overview of control and grid synchronization for distributed power generation systems. IEEE Trans. Ind. Electron. 53, 5, 1398–1409 (2006).
Hikihara, T., Sawada, T. & Funaki, T. Enhanced entrainment of synchronous inverters for distributed power sources. IEICE Trans. Fund. Electr. E90, 11, 2516–2525 (2007).
Bullmore, E. & Sporns, O. Complex brain networks: graph theoretical analysis of structural and functional systems. Nat. Rev. Neurosci. 10, 186–198 (2009).
Albert, R., Albert, I. & Nakarado, G. L. Structural vulnerability of the North American power grid. Phys. Rev. E 69, 025103(R) (2004).
Guckenheimer, J. & Holmes, P. Nonlinear Oscillations, Dynamical Systems and Bifurcations of Vector Fields. (Springer, 1983).
Acknowledgements
The authors thank J. Almendral, T. Hikihara, T. Kobayashi, H. Kori, N. Masuda, Y. Susuki and K. Tsumoto for their valuable comments. This research was supported by the Aihara Innovative Mathematical Modelling Project, the Japan Society for the Promotion of Science (JSPS) through the “Funding Program for World-Leading Innovative R&D on Science and Technology (FIRST Program),” initiated by the Council for Science and Technology Policy (CSTP).
Author information
Authors and Affiliations
Contributions
All authors conceived and designed the research. G.T. carried out the numerical experiments. G.T. and K.M. worked out the theoretical analyses. All authors wrote the manuscript.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Electronic supplementary material
Supplementary Information
Supplementary Information
Rights and permissions
This work is licensed under a Creative Commons Attribution-NonCommercial-ShareALike 3.0 Unported License. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-sa/3.0/
About this article
Cite this article
Tanaka, G., Morino, K. & Aihara, K. Dynamical robustness in complex networks: the crucial role of low-degree nodes. Sci Rep 2, 232 (2012). https://doi.org/10.1038/srep00232
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep00232
This article is cited by
-
Best influential spreaders identification using network global structural properties
Scientific Reports (2021)
-
Rhythmicity and firing modes in modular neuronal network under electromagnetic field
Nonlinear Dynamics (2021)
-
Chemical synaptic multiplexing enhances rhythmicity in neuronal networks
Nonlinear Dynamics (2019)
-
Core-like groups result in invalidation of identifying super-spreader by k-shell decomposition
Scientific Reports (2015)
-
Random and Targeted Interventions for Epidemic Control in Metapopulation Models
Scientific Reports (2014)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.