Skip to main content

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

  • Article
  • Published:

Gene expression model inference from snapshot RNA data using Bayesian non-parametrics

Nature Computational Science volume 3, pages 174–183 (2023)Cite this article

Subjects

A preprint version of the article is available at bioRxiv.

Abstract

Gene expression models, which are key towards understanding cellular regulatory response, underlie observations of single-cell transcriptional dynamics. Although RNA expression data encode information on gene expression models, existing computational frameworks do not perform simultaneous Bayesian inference of gene expression models and parameters from such data. Rather, gene expression models—composed of gene states, their connectivities and associated parameters—are currently deduced by pre-specifying gene state numbers and connectivity before learning associated rate parameters. Here we propose a method to learn full distributions over gene states, state connectivities and associated rate parameters, simultaneously and self-consistently from single-molecule RNA counts. We propagate noise from fluctuating RNA counts over models by treating models themselves as random variables. We achieve this within a Bayesian non-parametric paradigm. We demonstrate our method on the Escherichia coli lacZ pathway and the Saccharomyces cerevisiae STL1 pathway, and verify its robustness on synthetic data.

This is a preview of subscription content, access via your institution

Access options

Buy this article

  • Purchase on Springer Link
  • Instant access to full article PDF
Buy now

Prices may be subject to local taxes which are calculated during checkout

Fig. 1: Schematic of gene expression models.
Fig. 2: Accurate inference for a variety of gene expression models derived from synthetic data.
Fig. 3: Robustness analysis with respect to the quantity of data.
Fig. 4: Inference on data from E. coli in slow-growth media.
Fig. 5: Non-parametric inference on fast-growth E. coli data.
Fig. 6: Inference on S. cerevisiae data.

Similar content being viewed by others

Data availability

Source Data for Figs. 1–6 and Extended Data Figs. 1 and 2 is available with this paper, as well as online at ref. 114.

Code availability

Our custom MATLAB code is available at ref. 114.

References

  1. Xu, H., Skinner, S. O., Sokac, A. M. & Golding, I. Stochastic kinetics of nascent RNA. Phys. Rev. Lett. 117, 128101 (2016).

    Article  Google Scholar 

  2. Symmons, O. & Raj, A. What’s luck got to do with it: single cells, multiple fates, and biological nondeterminism. Mol. Cell 62, 788–802 (2016).

    Article  Google Scholar 

  3. Kumar, R. M. et al. Deconstructing transcriptional heterogeneity in pluripotent stem cells. Nature 516, 56–61 (2014).

    Article  Google Scholar 

  4. Emert, B. L. et al. Variability within rare cell states enables multiple paths toward drug resistance. Nature Biotechnol. 39, 865–876 (2021).

    Article  Google Scholar 

  5. Mutryn, M. F., Brannick, E. M., Fu, W., Lee, W. R. & Abasht, B. Characterization of a novel chicken muscle disorder through differential gene expression and pathway analysis using RNA-sequencing. BMC Genomics 16, 1–19 (2015).

    Article  Google Scholar 

  6. Garrett-Bakelman, F. E. & Melnick, A. M. Mutant IDH: a targetable driver of leukemic phenotypes linking metabolism, epigenetics and transcriptional regulation. Epigenomics 8, 945–957 (2016).

    Article  Google Scholar 

  7. Lee, T. I. & Young, R. A. Transcriptional regulation and its misregulation in disease. Cell 152, 1237–1251 (2013).

    Article  Google Scholar 

  8. Neuert, G. et al. Systematic identification of signal-activated stochastic gene regulation. Science 339, 584–587 (2013).

    Article  Google Scholar 

  9. Cvekl, A. & Duncan, M. K. Genetic and epigenetic mechanisms of gene regulation during lens development. Prog. Retin. Eye Res. 26, 555–597 (2007).

    Article  Google Scholar 

  10. Georgiadi, A. & Kersten, S. Mechanisms of gene regulation by fatty acids. Adv. Nutr. 3, 127–134 (2012).

    Article  Google Scholar 

  11. Femino, A. M., Fay, F. S., Fogarty, K. & Singer, R. H. Visualization of single RNA transcripts in situ. Science 280, 585–590 (1998).

    Article  Google Scholar 

  12. Kalisky, T. & Quake, S. R. Single-cell genomics. Nat. Methods 8, 311–314 (2011).

    Article  Google Scholar 

  13. Dattani, J. & Barahona, M. Stochastic models of gene transcription with upstream drives: exact solution and sample path characterization. J. R. Soc. Interface 14, 20160833 (2017).

    Article  Google Scholar 

  14. Cao, Y., Terebus, A. & Liang, J. State space truncation with quantified errors for accurate solutions to discrete chemical master equation. Bull. Math. Biol. 78, 617–661 (2016).

    Article  MathSciNet  MATH  Google Scholar 

  15. Klindziuk, A. & Kolomeisky, A. B. Theoretical investigation of transcriptional bursting: a multistate approach. J. Phys. Chem. B 122, 11969–11977 (2018).

    Article  Google Scholar 

  16. Golding, I., Paulsson, J., Zawilski, S. M. & Cox, E. C. Real-time kinetics of gene activity in individual bacteria. Cell 123, 1025–1036 (2005).

    Article  Google Scholar 

  17. So, L.-H. et al. General properties of transcriptional time series in Escherichia coli. Nat. Genet. 43, 554–560 (2011).

    Article  Google Scholar 

  18. Shaffer, S. M. et al. Memory sequencing reveals heritable single-cell gene expression programs associated with distinct cellular behaviors. Cell 182, 947–959 (2020).

    Article  Google Scholar 

  19. Junker, J. P. & van Oudenaarden, A. Every cell is special: genome-wide studies add a new dimension to single-cell biology. Cell 157, 8–11 (2014).

    Article  Google Scholar 

  20. Raj, A., Peskin, C. S., Tranchina, D., Vargas, D. Y. & Tyagi, S. Stochastic mRNA synthesis in mammalian cells. PLoS Biol. 4, e309 (2006).

    Article  Google Scholar 

  21. Cao, Z. & Grima, R. Analytical distributions for detailed models of stochastic gene expression in eukaryotic cells. Proc. Natl Acad. Sci. USA 117, 4682–4692 (2020).

    Article  Google Scholar 

  22. Fujita, K., Iwaki, M. & Yanagida, T. Transcriptional bursting is intrinsically caused by interplay between RNA polymerases on DNA. Nat. Commun. 7, 1–10 (2016).

    Article  Google Scholar 

  23. Suter, D. M. et al. Mammalian genes are transcribed with widely different bursting kinetics. Science 332, 472–474 (2011).

    Article  Google Scholar 

  24. Sepúlveda, L. A., Xu, H., Zhang, J., Wang, M. & Golding, I. Measurement of gene regulation in individual cells reveals rapid switching between promoter states. Science 351, 1218–1222 (2016).

    Article  Google Scholar 

  25. Xu, H., Sepúlveda, L. A., Figard, L., Sokac, A. M. & Golding, I. Combining protein and mRNA quantification to decipher transcriptional regulation. Nat. Methods 12, 739–742 (2015).

    Article  Google Scholar 

  26. Vo, H. D., Fox, Z., Baetica, A. & Munsky, B. Bayesian estimation for stochastic gene expression using multifidelity models. J. Phys. Chem. B 123, 2217–2234 (2019).

    Article  Google Scholar 

  27. Munsky, B., Neuert, G. & Van Oudenaarden, A. Using gene expression noise to understand gene regulation. Science 336, 183–187 (2012).

    Article  MathSciNet  MATH  Google Scholar 

  28. Braichenko, S., Holehouse, J. & Grima, R. Distinguishing between models of mammalian gene expression: telegraph-like models versus mechanistic models. J. R. Soc. Interface 18, 20210510 (2021).

    Article  Google Scholar 

  29. Kuha, J. AIC and BIC: comparisons of assumptions and performance. Sociol. Methods Res. 33, 188–229 (2004).

    Article  MathSciNet  Google Scholar 

  30. Vrieze, S. Model selection and psychological theory: a discussion of the differences between the Akaike information criterion (AIC) and the Bayesian information criterion (BIC). Psychol. Methods 17, 228–243 (2012).

    Article  Google Scholar 

  31. Sanchez, A. & Golding, I. Genetic determinants and cellular constraints in noisy gene expression. Science 342, 1188–1193 (2013).

    Article  Google Scholar 

  32. Kandhavelu, M., Häkkinen, A., Yli-Harja, O. & Ribeiro, A. Single-molecule dynamics of transcription of the lar promoter. Phys. Biol. 9, 026004 (2012).

    Article  Google Scholar 

  33. Figueroa-López, J. E. & Levine, M. Nonparametric regression with rescaled time series errors. J. Time Ser. Anal. 34, 345–361 (2013).

    Article  MathSciNet  MATH  Google Scholar 

  34. Dahl, C. M. & Levine, M. Nonparametric estimation of volatility models with serially dependent innovations. Stat. Probab. Lett. 76, 2007–2016 (2006).

    Article  MathSciNet  MATH  Google Scholar 

  35. Cai, T. T., Levine, M. & Wang, L. Variance function estimation in multivariate nonparametric regression with fixed design. J. Multivar. Anal. 100, 126–136 (2009).

    Article  MathSciNet  MATH  Google Scholar 

  36. Liu, L., Levine, M. & Zhu, Y. A functional EM algorithm for mixing density estimation via nonparametric penalized likelihood maximization. J. Comput. Graph. Stat. 18, 481–504 (2009).

    Article  MathSciNet  Google Scholar 

  37. Wang, L., Brown, L. D., Cai, T. T. & Levine, M. Effect of mean on variance function estimation in nonparametric regression. Ann. Stat. 36, 646–664 (2008).

    Article  MathSciNet  MATH  Google Scholar 

  38. Brown, L. D. & Levine, M. Variance estimation in nonparametric regression via the difference sequence method. Ann. Stat. 35, 2219–2232 (2007).

    Article  MathSciNet  MATH  Google Scholar 

  39. Levine, M. Bandwidth selection for a class of difference-based variance estimators in the nonparametric regression: a possible approach. Comput. Stat. Data Anal. 50, 3405–3431 (2006).

    Article  MathSciNet  MATH  Google Scholar 

  40. Zhou, X., Wang, X. & Dougherty, E. R. Gene selection using logistic regressions based on AIC, BIC and MDL criteria. New Math. Nat. Comput. 01, 129–145 (2005).

    Article  MathSciNet  MATH  Google Scholar 

  41. Lin, Y. T. & Buchler, N. E. Exact and efficient hybrid Monte Carlo algorithm for accelerated Bayesian inference of gene expression models from snapshots of single-cell transcripts. J. Chem. Phys. 151, 024106 (2019).

    Article  Google Scholar 

  42. Fröhlich, F. et al. Multi-experiment nonlinear mixed effect modeling of single-cell translation kinetics after transfection. npj Syst. Biol. Appl. 4, 1–12 (2018).

    Article  Google Scholar 

  43. Jones, D. & Elf, J. Bursting onto the scene? Exploring stochastic mRNA production in bacteria. Curr. Opin. Microbiol. 45, 124–130 (2018).

    Article  Google Scholar 

  44. Boeger, H., Griesenbeck, J. & Kornberg, R. D. Nucleosome retention and the stochastic nature of promoter chromatin remodeling for transcription. Cell 133, 716–726 (2008).

    Article  Google Scholar 

  45. Weber, L., Raymond, W. & Munsky, B. Identification of gene regulation models from single-cell data. Phys. Biol. 15, 055001 (2018).

    Article  Google Scholar 

  46. Vo, H. D., Fox, Z., Baetica, A. & Munsky, B. Bayesian estimation for stochastic gene expression using multifidelity models. J. Phys. Chem. B 123, 2217–2234 (2019).

    Article  Google Scholar 

  47. Munsky, B., Li, G., Fox, Z. R., Shepherd, D. P. & Neuert, G. Distribution shapes govern the discovery of predictive models for gene regulation. Proc. Natl Acad. Sci. USA 115, 7533–7538 (2018).

    Article  Google Scholar 

  48. Mugler, A., Walczak, A. M. & Wiggins, C. H. Spectral solutions to stochastic models of gene expression with bursts and regulation. Phys. Rev. E 80, 041921 (2009).

    Article  Google Scholar 

  49. Zhou, T. & Zhang, J. Analytical results for a multistate gene model. SIAM J. Appl. Math. 72, 789–818 (2012).

    Article  MathSciNet  MATH  Google Scholar 

  50. Khanin, R. & Higham, D. J. Chemical master equation and langevin regimes for a gene transcription model. Theor. Comput. Sci. 408, 31–40 (2008).

    Article  MathSciNet  MATH  Google Scholar 

  51. Fox, Z., Neuert, G. & Munsky, B. Finite state projection based bounds to compare chemical master equation models using single-cell data. J. Chem. Phys. 145, 074101 (2016).

    Article  Google Scholar 

  52. Gómez-Schiavon, M., Chen, L.-F., West, A. E. & Buchler, N. E. Bayfish: Bayesian inference of transcription dynamics from population snapshots of single-molecule RNA fish in single cells. Genome Biol. 18, 1–12 (2017).

    Article  Google Scholar 

  53. Cao, Z. & Grima, R. Accuracy of parameter estimation for auto-regulatory transcriptional feedback loops from noisy data. J. R. Soc. Interface 16, 20180967 (2019).

    Article  Google Scholar 

  54. Jazani, S., Sgouralis, I. & Pressé, S. A method for single molecule tracking using a conventional single-focus confocal setup. J. Chem. Phys. 150, 114108 (2019).

    Article  Google Scholar 

  55. Pressé, S., Lee, J. & Dill, K. A. Extracting conformational memory from single-molecule kinetic data. J. Phys. Chem. B 117, 495–502 (2013).

    Article  Google Scholar 

  56. Pressé, S. et al. Single molecule conformational memory extraction: P5ab RNA hairpin. J. Phys. Chem. B 118, 6597–6603 (2014).

    Article  Google Scholar 

  57. Ferguson, T. A Bayesian analysis of some nonparametric problems. Ann. Stat. 1, 209 (1973).

    Article  MathSciNet  MATH  Google Scholar 

  58. Hjort, N. Nonparametric Bayes estimators based on beta processes in models for life history data. Ann. Stat. 18, 1259–1294 (1990).

  59. Bryan IV, J. S., Sgouralis, I. & Pressé, S. Diffraction-limited molecular cluster quantification with Bayesian nonparametrics. Nat. Comput. Sci. 2, 102–111 (2022).

    Article  Google Scholar 

  60. Fox, E., Sudderth, E., Jordan, M. & Willsky, A. Bayesian nonparametric methods for learning Markov switching processes. IEEE Signal Process. Mag. 27, 43–54 (2010).

    Google Scholar 

  61. Sgouralis, I. & Pressé, S. An introduction to infinite HMMs for single-molecule data analysis. Biophys. J. 112, 2021–2029 (2017).

    Article  Google Scholar 

  62. Wang, M., Zhang, J., Xu, H. & Golding, I. Measuring transcription at a single gene copy reveals hidden drivers of bacterial individuality. Nat. Microbiol. 4, 2118–2127 (2019).

    Article  Google Scholar 

  63. Li, G. & Neuert, G. Multiplex RNA single molecule FISH of inducible mRNAs in single yeast cells. Sci. Data 6, 1–9 (2019).

    Article  Google Scholar 

  64. Munsky, B. & Khammash, M. The finite state projection algorithm for the solution of the chemical master equation. J. Chem. Phys. 124, 044104 (2006).

    Article  MATH  Google Scholar 

  65. Munsky, B., Fox, Z. & Neuert, G. Integrating single-molecule experiments and discrete stochastic models to understand heterogeneous gene transcription dynamics. Methods 85, 12–21 (2015).

    Article  Google Scholar 

  66. Fei, J. et al. Determination of in vivo target search kinetics of regulatory noncoding RNA. Science 347, 1371–1374 (2015).

    Article  Google Scholar 

  67. Kilic, Z., Sgouralis, I. & Pressé, S. Generalizing HMMs to continuous time for fast kinetics: hidden Markov jump processes. Biophys. J. 120, 409–423 (2021).

    Article  Google Scholar 

  68. Tavakoli, M. et al. Pitching single-focus confocal data analysis one photon at a time with Bayesian nonparametrics. Phys. Rev. X 10, 011021 (2020).

    Google Scholar 

  69. Skinner, S. O., Sepúlveda, L. A., Xu, H. & Golding, I. Measuring mRNA copy number in individual Escherichia coli cells using single-molecule fluorescent in situ hybridization. Nat. Protoc. 8, 1100–1113 (2013).

    Article  Google Scholar 

  70. Wang, G., Moffitt, J. R. & Zhuang, X. Multiplexed imaging of high-density libraries of RNAs with MERFISH and expansion microscopy. Sci. Rep. 8, 1–13 (2018).

    Google Scholar 

  71. Kramer, A., Calderhead, B. & Radde, N. Hamiltonian Monte Carlo methods for efficient parameter estimation in steady state dynamical systems. BMC Bioinform. 15, 253 (2014).

    Article  Google Scholar 

  72. Berger, M. & ten Wolde, P. R. Robust replication initiation from coupled homeostatic mechanisms. Preprint at https://arxiv.org/abs/2106.03674 (2021).

  73. Foreman, R. & Wollman, R. Mammalian gene expression variability is explained by underlying cell state. Mol. Syst. Biol. 16, e9146 (2020).

    Article  Google Scholar 

  74. Ietswaart, R., Rosa, S., Wu, Z., Dean, C. & Howard, M. Cell-size-dependent transcription of FLC and its antisense long non-coding RNA COOLAIR explain cell-to-cell expression variation. Cell Syst. 4, 622–635 (2017).

    Article  Google Scholar 

  75. Kau, T. R. & Silver, P. A. Nuclear transport as a target for cell growth. Drug Discov. Today 8, 78–85 (2003).

    Article  Google Scholar 

  76. Komeili, A. & O’Shea, E. K. Nuclear transport and transcription. Curr. Opin. Cell Biol. 12, 355–360 (2000).

    Article  Google Scholar 

  77. Wheat, J. C. et al. Single-molecule imaging of transcription dynamics in somatic stem cells. Nature 583, 431–436 (2020).

    Article  Google Scholar 

  78. Lubeck, E., Coskun, A. F., Zhiyentayev, T., Ahmad, M. & Cai, L. Single-cell in situ RNA profiling by sequential hybridization. Nat. Methods 11, 360–361 (2014).

    Article  Google Scholar 

  79. Chen, K. H., Boettiger, A. N., Moffitt, J. R., Wang, S. & Zhuang, X. Spatially resolved, highly multiplexed RNA profiling in single cells. Science 348, aaa6090 (2015).

  80. Vo, H. & Sidje, R. B. Improved Krylov-FDP method for solving the chemical master equation. In Proc. World Congress on Engineering and Computer Science 2016 Vol II 521–526 (WCECS, 2016).

  81. Vo, H. D. & Munsky, B. E. A parallel implementation of the finite state projection algorithm for the solution of the chemical master equation. Preprint at bioRxiv https://www.biorxiv.org/content/10.1101/2020.06.30.180273v2 (2020).

  82. Dufera, T. T. Deep neural network for system of ordinary differential equations: vectorized algorithm and simulation. Mach. Learn. Appl. 5, 100058 (2021).

  83. Kazeev, V., Khammash, M., Nip, M. & Schwab, C. Direct solution of the chemical master equation using quantized tensor trains. PLoS Comput. Biol. 10, e1003359 (2014).

    Article  Google Scholar 

  84. Jiang, Q. et al. Neural network aided approximation and parameter inference of non-Markovian models of gene expression. Nat. Commun. 12, 1–12 (2021).

    Article  Google Scholar 

  85. Öcal, K., Gutmann, M. U., Sanguinetti, G. & Grima, R. Inference and uncertainty quantification of stochastic gene expression via synthetic models. J. R. Soc. Interface 19, 20220153 (2022).

    Article  Google Scholar 

  86. Öcal, K., Grima, R. & Sanguinetti, G. Parameter estimation for biochemical reaction networks using Wasserstein distances. J. Phys. A 53, 034002 (2019).

    Article  MathSciNet  MATH  Google Scholar 

  87. Kilic, Z. et al. Extraction of rapid kinetics from smfret measurements using integrative detectors. Cell Rep. Phys. Sci. 2, 100409 (2021).

    Article  Google Scholar 

  88. Tanouchi, Y. et al. Long-term growth data of escherichia coli at a single-cell level. Sci. Data 4, 1–5 (2017).

    Article  Google Scholar 

  89. Jia, C. & Grima, R. Frequency domain analysis of fluctuations of mrna and protein copy numbers within a cell lineage: theory and experimental validation. Phys. Rev. X 11, 021032 (2021).

    Google Scholar 

  90. Johansson, H. E., Liljas, L. & Uhlenbeck, O. C. in Seminars in Virology Vol. 8, 176–185 (Elsevier, 1997).

  91. Bertrand, E. et al. Localization of ASH1 mRNA particles in living yeast. Mol. Cell 2, 437–445 (1998).

    Article  Google Scholar 

  92. Morisaki, T. et al. Real-time quantification of single rna translation dynamics in living cells. Science 352, 1425–1429 (2016).

    Article  Google Scholar 

  93. Corrigan, A. M., Tunnacliffe, E., Cannon, D. & Chubb, J. R. A continuum model of transcriptional bursting. Elife 5, e13051 (2016).

    Article  Google Scholar 

  94. Donovan, B. T. et al. Live-cell imaging reveals the interplay between transcription factors, nucleosomes, and bursting. EMBO J. 38, e100809 (2019).

    Article  Google Scholar 

  95. Liu, J. et al. Real-time single-cell characterization of the eukaryotic transcription cycle reveals correlations between rna initiation, elongation, and cleavage. PLoS Comput. Biol. 17, e1008999 (2021).

    Article  Google Scholar 

  96. Zechner, C., Unger, M., Pelet, S., Peter, M. & Koeppl, H. Scalable inference of heterogeneous reaction kinetics from pooled single-cell recordings. Nat. Methods 11, 197–202 (2014).

    Article  Google Scholar 

  97. Liu, B. et al. Influence of fluorescent protein maturation on fret measurements in living cells. ACS Sens. 3, 1735–1742 (2018).

    Article  Google Scholar 

  98. Dong, G. Q. & McMillen, D. R. Effects of protein maturation on the noise in gene expression. Phys. Rev. E 77, 021908 (2008).

    Article  Google Scholar 

  99. Hebisch, E., Knebel, J., Landsberg, J., Frey, E. & Leisner, M. High variation of fluorescence protein maturation times in closely related escherichia coli strains. PLoS ONE 8, e75991 (2013).

    Article  Google Scholar 

  100. Balleza, E., Kim, J. M. & Cluzel, P. Systematic characterization of maturation time of fluorescent proteins in living cells. Nat. Methods 15, 47–51 (2018).

    Article  Google Scholar 

  101. Elf, J. & Barkefors, I. Single-molecule kinetics in living cells. Annu. Rev. Biochem. 88, 635–659 (2019).

    Article  Google Scholar 

  102. Cialek, C. A., Koch, A. L., Galindo, G. & Stasevich, T. J. Lighting up single-mrna translation dynamics in living cells. Curr. Opin. Genet. Dev. 61, 75–82 (2020).

    Article  Google Scholar 

  103. Boka, A. P., Mukherjee, A. & Mir, M. Single-molecule tracking technologies for quantifying the dynamics of gene regulation in cells, tissue and embryos. Development 148, dev199744 (2021).

    Article  Google Scholar 

  104. Li, W., Maekiniemi, A. & Singer, R. H. Imaging mRNAs with corrected RNA stability. FASEB J. https://doi.org/10.1096/fasebj.2022.36.S1.0R370 (2022).

  105. Hammar, P. et al. Direct measurement of transcription factor dissociation excludes a simple operator occupancy model for gene regulation. Nat. Genet. 46, 405–408 (2014).

    Article  Google Scholar 

  106. Schuh, L. et al. Gene networks with transcriptional bursting recapitulate rare transient coordinated high expression states in cancer. Cell Syst. 10, 363–378.e12 (2020).

    Article  Google Scholar 

  107. Gillespie, D. Exact stochastic simulation of coupled chemical reactions. J. Phys. Chem. 81, 2340 (1977).

    Article  Google Scholar 

  108. Cheng, Y., Li, D. & Jiang, W. The exact inference of Beta process and Beta Bernoulli process from finite observations. Comput. Model. Eng. Sci. 121, 49–82 (2019).

    Google Scholar 

  109. Thibaux, R. & Jordan, M. I. Hierarchical beta processes and the Indian buffet process. In Proc. Eleventh International Conference on Artificial Intelligence and Statistics (eds Lawrence, N. & Reid, M.) 564–571 (MLResearch Press, 2007).

  110. Green, P. J. Reversible jump Markov chain Monte Carlo computation and Bayesian model determination. Biometrika 82, 711–732 (1995).

    Article  MathSciNet  MATH  Google Scholar 

  111. Christen, J. A. & Fox, C. Markov chain Monte Carlo using an approximation. J. Comput. Graph. Stat. 14, 795–810 (2005).

    Article  MathSciNet  Google Scholar 

  112. Hastings, W. Monte Carlo sampling methods using Markov chains and their applications. Biometrika 57, 97–109 (1970).

    Article  MathSciNet  MATH  Google Scholar 

  113. Smith, A. & Roberts, G. Bayesian computation via the Gibbs sampler and related Markov chain Monte Carlo methods. J. R. Stat. Soc. B 55, 3–23 (1993).

    MathSciNet  MATH  Google Scholar 

  114. mcschweiger Labpresse/gene_exp_nonpara: tnitial release. Zenodo https://doi.org/10.5281/zenodo.7425217 (2022).

  115. Gillespie, D. A general method for numerically simulating the stochastic time evolution of coupled chemical reactions. J. Comput. Phys. 22, 403–434 (1976).

    Article  MathSciNet  Google Scholar 

  116. Stephens, M. Dealing with label switching in mixture models. J. R. Stat. Soc. Ser. B 62, 795–809 (2000).

    Article  MathSciNet  MATH  Google Scholar 

  117. Cao, Y. Munkres assignment algorithm. MATLAB Central File Exchange https://www.mathworks.com/matlabcentral/fileexchange/20328-munkres-assignment-algorithm (2022).

Download references

Acknowledgements

We thank I. Golding for providing the experimental data analyzed herein. We thank I. Sgouralis, Z. Fox and B. Munsky for interesting discussions and insights. D.S. acknowledges support from the NIH NHLBI (R01HL068702) and NIH BRAIN (RF1MH128867), and S.P. acknowledges support from NIH NIGMS (R01GM130745) and NIH NIGMS (R01GM134426).

Author information

Author notes

  1. These authors contributed equally: Zeliha Kilic, Max Schweiger.

Authors and Affiliations

  1. Department of Structural Biology, St. Jude Children’s Research Hospital, Memphis, TN, USA

    Zeliha Kilic

  2. Center for Biological Physics, ASU, Tempe, AZ, USA

    Max Schweiger, Camille Moyer, Douglas Shepherd & Steve Pressé

  3. Department of Physics, ASU, Tempe, AZ, USA

    Max Schweiger, Douglas Shepherd & Steve Pressé

  4. School of Mathematics and Statistical Sciences, ASU, Tempe, AZ, USA

    Camille Moyer

  5. School of Molecular Sciences, ASU, Tempe, AZ, USA

    Steve Pressé

Authors
  1. Zeliha Kilic
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Max Schweiger
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Camille Moyer
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Douglas Shepherd
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Steve Pressé
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

Z.K. and C.M. developed the Bayesian non-parametric inference algorithm and software with input from D.S. and S.P. M.S. further developed the existing analysis software and analyzed the data. M.S. created all the figures in the paper with input from all authors. All authors wrote the manuscript. Z.K., M.S., C.M. and S.P. conceived the research, and D.S. and S.P. oversaw all aspects of the project.

Corresponding authors

Correspondence to Douglas Shepherd or Steve Pressé.

Ethics declarations

Competing interests

The authors declare no competing interests.

Peer review

Peer review information

Nature Computational Science thanks the anonymous reviewers for their contribution to the peer review of this work. Primary Handling Editor: Ananya Rastogi, in collaboration with the Nature Computational Science team.

Additional information

Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Extended data

Extended Data Fig. 1 Robustness analysis: transcription rate.

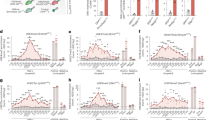
Shown are posterior distributions over: production rates βl, and transition rates \({k}_{{\sigma }_{l}\to {\sigma }_{{l}^{{\prime} }}}\). Across columns, the breadth of the distributions is comparable for a model containing two gene states, under various maximum ground-truth production rates. Again, the posterior maximum closely matches the ground truth, demonstrating the method’s robustness under quantitative changes in RNA count distribution. As before, each data point was generated using the Gillespie stochastic simulation algorithm, with weak limit set to L = 8 (as per Fig. 2). Rates in each column are inferred for 600 cells observed per time point with 20 collection times at [0, 10, 20, 30, 40, 50, 60, 70, 80, 90, 120, 180, 240, 360, 480, 600, 1200, 3600] (s).

Source data

Extended Data Fig. 2 Robustness analysis: various kinetic rates.

Shown are posterior distributions over rates for two-state gene expression models obeying a variety of qualitative behaviors. a) illustrates important examples of the qualitative behaviors in the RNA count distribution we wish to probe. b) depicts posterior histograms of rates, with each column arising from distinct data, as indicated in a). As before, each data point was generated using the Gillespie stochastic simulation algorithm, and the weak limit is set to L = 8 (as per Fig. 2). Rates in each column are inferred for 2000 cells observed per time point with 20 collection times at [0, 10, 20, 30, 40, 50, 60, 70, 80, 90, 120, 180, 240, 360, 480, 600, 1200, 3600] (s).

Source data

Supplementary information

Supplementary Information

Supplementary information and Figs. 1–18.

Reporting Summary

Source data

Source Data Fig. 2

Statistical source data.

Source Data Fig. 3

Statistical source data.

Source Data Fig. 4

Statistical source data.

Source Data Fig. 5

Statistical source data.

Source Data Fig. 6

Statistical source data.

Source Data Extended Data Fig. 1

Statistical source data.

Source Data Extended Data Fig. 2

Statistical source data.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Kilic, Z., Schweiger, M., Moyer, C. et al. Gene expression model inference from snapshot RNA data using Bayesian non-parametrics. Nat Comput Sci 3, 174–183 (2023). https://doi.org/10.1038/s43588-022-00392-0

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1038/s43588-022-00392-0

This article is cited by

Search

Advanced search

Quick links

Nature Briefing

Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.

Get the most important science stories of the day, free in your inbox. Sign up for Nature Briefing