Main

Networks are used to investigate a wide range of technological, social and biological systems1. Key factors for their success are the availability of powerful mathematical and computational analysis tools, but also their intuitive visual interpretation. For example, the central position of genes within molecular networks indicates essential cellular processes2, densely connected clusters represent functional complexes3, and global patterns, such as the ring-like architecture of co-regulation networks, have been found to reflect principles of cellular organization4. However, the full potential of network visualizations for exploring complex systems is limited by several conceptual and practical challenges. (1) Networks do not have a natural two- or three-dimensional (2D or 3D) embedding. Any network layout thus involves a choice of which aspects of the high-dimensional pairwise relationships are visually represented, and which are not. (2) In widely used layout algorithms, such as force-directed methods, this choice is made in an implicit and thus intransparent fashion, often based on subjective, esthetic criteria. This lack of a clear relationship between structural network characteristics and node positioning makes the resulting layouts difficult to interpret. (3) Likewise, there are no layout algorithms available that allow for explicitly representing a given network characteristic. (4) Finally, the big size of many real-world networks is a key limiting factor for producing comprehensible layouts, leading to proverbial hair-ball visualizations. In this Brief Communication we introduce a framework for generating network layouts that address these challenges by using dimensionality reduction to directly encode network properties into node positions. Not only can structural network properties be visually encoded in this fashion, but also external information reflecting the functional characteristics of nodes or links.

We propose the following procedure (Fig. 1a). For a given network, we first compile a set of F features for each of N nodes, incorporating any structural or functional characteristic we wish to be visually reflected in the final layout. The resulting (N × F) feature matrix is then converted into an (N × N) similarity matrix, which serves as input to dimensionality reduction methods to compute 2D or 3D embeddings. These embeddings can either be used directly as node coordinates, resulting in network layouts we termed portraits. Alternately, embeddings on 2D surfaces can be further extended towards 3D topographic or geodesic maps by using the third dimension for an additional variable of choice. The topographic map extends a flat 2D embedding by an additional z coordinate, and geodesic maps introduce an additional radial coordinate in spherical embeddings. In total, our framework thus offers four different maps in two and three dimensions (Fig. 1b). The key advantage of our framework, offering both versatility and interpretability, is its ability to incorporate and explicitly display various desired node characteristics or node pair relationships. We implemented five examples that demonstrate the diversity of potential layouts. (1) The global layout uses network propagation for an efficient, high-resolution representation of pairwise network distances. (2) The local layout emphasizes similar connection patterns between node pairs. (3) The importance layout combines several metrics for the overall importance of a node, such as degree, betweenness, closeness and eigenvector centrality. (4) Functional layouts depict node similarities according to external node features. (5) Combined layouts allow for tuning between layouts that are dominated by either structural or functional features.

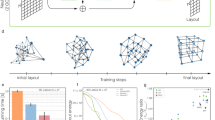
Fig. 1: Framework of interpretable network maps.
figure 1

a, Overview. A node similarity matrix reflecting any network features to be visually represented is embedded into 2D or 3D geometries using dimensionality reduction methods. b, Schematic depiction of the resulting four types of network map: 2D and 3D network portraits directly use the outputs of the dimensionality reduction; topographic and geodesic maps incorporate an additional z or radial variable, respectively. c, The network models used for benchmarking: Cayley tree, cubic grid and torus lattice. d–f, Model network portraits based on global (d), local (e) and importance (f) layouts. The global layouts recapitulate the expected global shape according to pairwise node distances. The local layouts reveal bi- and multipartite network structures. The importance layouts cluster nodes with similar structural importance. g, Comparison of network-based and Euclidean layout distance for all node pairs in a cubic grid (N = 1,000) for the global layout, two force-directed algorithms and node2vec. All layouts achieve high correlation (Pearson’s ρglob = 0.99, ρnode2vec = 0.97, ρforce,nx = 0.97, ρforce,igraph = 0.98). Boxes summarize values of all n node pairs at network distance d, with n ranging from n = 4 at distance d = 27 (for corner node pairs) to n = 46,852 for d = 9. Whiskers denote the values for the minimum, first, second and third quartiles and maximum. h, Comparison of the final correlations for cubic grids of increasing size when limiting the wall clock running time of the algorithms to the running time of the global layout. i, Computational wall times that the respective algorithms require to achieve the same correlation as the global layout for cube grids of increasing size.

Source data

Full size image

To illustrate and benchmark our framework, we first applied it to easily interpretable model networks: (1) a Cayley tree, (2) a cubic grid and (3) a torus lattice (Fig. 1c). The Cayley tree is organized in hierarchical levels. All nodes except for those in the outermost level have the same number of neighbors (degree k = 3), and all nodes within the same level have identical centrality values. The cubic lattice contains four structurally different node groups: nodes at the corner (k = 3), along the 12 edges (k = 4), on the six faces (k = 5) or in the interior (k = 6). In the torus lattice, all nodes are equivalent in terms of all structural characteristics, including their degree (k = 4) and centrality metrics. Note that the definition of none of the model networks involves any spatial embedding, so, in principle, no layout is in any formal sense more correct than any other. However, for all three network models, canonical layouts in two and three dimensions, respectively, exist, offering an intuitive visualization of their global architecture. Our global layout provides a good approximation for these idealizations (Fig. 1d). The local and importance layouts produce entirely different results, each highlighting distinct structural aspects of the model networks. In the local layouts, the nodes are sorted into groups with shared neighbors (Fig. 1e). This layout reveals bi- and multipartite network structures, resulting in two clusters in the lattice-based networks (cube and torus), and in alternating patterns reflecting the ternary structure of the Cayley tree. The importance layout identifies groups of nodes with the same network centralities (Fig. 1f). In the Cayley tree, all nodes of the same hierarchy are clustered, and in the cubic grid, nodes of the same type (corner, edge, face nodes) and layer are grouped. In the torus, all nodes have equivalent structural roles, thus resulting in a uniform point cloud.

The global layout incorporates random walk-based features similar to the graph embedding method node2vec5. Also, for small to moderate network sizes, standard force-directed algorithms6 produce layouts that recapitulate network distances between node pairs. We can therefore use these algorithms as performance benchmarks. Figure 1g shows good overall correlations between network-based node distances in cubic lattice networks and the respective layout distances (Extended Data Fig. 1). A comparison of the correlations obtained for the same computational running time shows a substantial drop for force-directed algorithms as the network size increases (Fig. 1h). Conversely, force-directed methods are orders of magnitudes slower for fixed layout quality (Fig. 1i).

We next apply our framework to a large real-world network. The human interactome consists of N = 16,376 nodes and M = 309,355 links, representing proteins and their physical interactions that underlie biological processes7,8. Although several structure-to-function relationships in the interactome are well documented9, they are difficult to decipher visually from conventional layouts. Our framework offers a solution to this challenge. Figure 2a shows a 2D network portrait of the interactome in the importance layout. Visual inspection of 2,918 known essential genes reveals a relationship between their structural importance within the interactome and their biological importance. Cancer driver genes, rare disease genes and genes involved in early development show the same trend (Extended Data Fig. 2a–c). Although this finding represents one of the cornerstones of network biology2, it could not be derived from standard layouts (Extended Data Fig. 3a). Similarly, the agglomeration of genes associated with the same disease in local interactome neighborhoods is well documented10, yet remains hidden in standard layouts (Extended Data Fig. 3b). We can use functional network portraits to visualize disease-associated genes and their interconnectivity (Fig. 2b). Although the node placement is purely driven by a functional characteristic, the underlying network structure can be inspected through the links. This supports the identification of structure-to-function relationships in an iterative cycle of data visualization, hypothesis generation and validation. In addition to disease gene interconnectivity, Fig. 2b also shows a prominent cluster of highly connected genes associated with multiple diseases (Extended Data Fig. 4). Finally, we can also generate layouts in which the node positions are determined by a combination of structural and functional features (see Extended Data Figs. 5 and 6 for applications to a model network and the interactome).

Fig. 2: Application to a large-scale, real-world biological network.
figure 2

a, Structural network portrait of the human interactome based on the importance layout. Essential genes and links between them are shown in blue and aggregate in the area of high centrality nodes (top right). b, Functional network portrait based on disease association similarity. Four diseases are highlighted. Only links between disease genes are shown. Although most disease genes are located in four clusters (links shown by thicker lines), a smaller number of pleiotropic genes associated with multiple diseases is located at the center of the network (Extended Data Fig. 4b). c, Topographic network map in top view (left) and side view (right) obtained from a 3D interactive visualization. The x–y plane is based on a 2D global layout, and the z axis displays the number of diseases associated with a particular gene. d, Green-screen composition of a user exploring a geodesic network map in a virtual reality environment13. Nodes are distributed on different spherical layers that reflect different biological roles. The center contains nodes to be functionally annotated, the enclosing layers contain genes associated with similar diseases and involved in relevant biological processes, respectively. Each individual layer is based on a functional layout emphasizing biological similarity, allowing the user to quickly identify the biological context of individual genes and their interactome neighborhood.

Source data

Full size image

Network maps with an additional quantity of interest depicted in the third dimension can be used to build application-specific visualizations. Figure 2c shows a 3D topographic map of the interactome, with a global layout on the x–y plane and the number of disease associations on the z axis, highlighting, for example, the prominent role of the tumor suppressor TP53 in many cancers11. The top view reveals several localized node clusters, which correspond to provincial hubs and their respective neighbors12. The side view shows the prominent role of the provincial hubs for diseases and their relationships, such as amyloid precursor protein (APP) and ELAV-like RNA binding protein (ELAVL1), which are located at the center of the respective interactome neighborhoods that are perturbed in the associated diseases13.

Figure 2d demonstrates how our framework can be utilized for generating network maps customized to the interactive annotation of rare genomic variants in a virtual reality environment14. The center sphere of the geodesic map contains 13 candidate genes that are suspected to cause a rare genetic disease in a particular patient. The enclosing spheres represent genes implicated in similar phenotypes or involved in related biological pathways, respectively, in a functional layout reflecting biological similarity. This allows for an efficient manual inspection of the biological context of the candidate genes.

The flexibility of our framework enables the development of customized network visualizations for a broad range of applications. In biology, for example, the introduced layouts may enhance existing tools for the integration and interpretation of diverse omics datasets15,16,17,18,19. Note that visual inspection alone will rarely suffice to conclusively show the presence of an observed structure-to-function relationship in a given network. Any hypothesis derived from a particular visualization thus requires an additional, more rigorous evaluation outside of our framework, for example, by statistical or experimental means.

Methods

A framework for creating interpretable network layouts and maps

Our pipeline consists of four basic steps. (1) The network of N nodes and M links is supplied in the form of a link list. (2) For each node in the network, we construct a vector of F features, resulting in an (N × F) feature matrix. The particular features that are used determine the layout. We introduce five such layouts, termed ‘global’, ‘local’, ‘importance’, ‘functional’ and ‘combined’ layouts, as detailed in the next sections. (3) The feature matrix is converted into an (N × N) similarity matrix, which serves as input for dimensionality reduction algorithms. The utility of dimensionality reduction techniques for network embedding is increasingly recognized, in particular for classification tasks and more recently also for visualizations20. We implemented the popular tools t-distributed neighbor embedding (t-SNE)21 and uniform manifold approximation and projection (UMAP)22, which offer embeddings in 2D and 3D Euclidean space, as well as embeddings on 2D surfaces, such as a sphere. (4) The node coordinates can either be used directly to lay out the network or can be further enhanced by an additional third dimension in the case of 2D embeddings. We termed the direct layouts ‘portraits’. Flat embeddings in 2D Euclidean space can be expanded into 3D topographic maps by using an additional, freely selectable variable as the z coordinate. Similarly, we can enhance embeddings on the surface of a sphere by introducing an additional radial variable, resulting in geodesic maps.

Global layout

In the global layout, each node is equipped with N features representing its network-based distances to all nodes in the network based on a random walk with the restart propagation method23. These random walk-based distances indicate how frequently a walker starting from node i and traveling along randomly chosen links will visit a given node j. Formally, we first determine the vector pi containing the visiting frequencies pi,j for all nodes j ∈ [1, N] starting from node i as seed for a random walk with restart probability r. These frequencies can be efficiently computed by matrix inversion according to the steady-state expression for a random walk with restart24. For all node pairs {n, m}, we then compute the cosine similarity S(n, m) between their respective visiting frequency vectors pn and pm and collect the results into an (N × N) similarity matrix Sglob that serves as input to the dimensionality reduction step of the pipeline.

Local layout

The local layout is based on the similarity of nodes in terms of shared neighbors. Two nodes that are connected to the exact same set of nodes are considered maximally similar, whereas nodes that do not have any common neighbors do not have any similarity. We can determine this similarity directly from the adjacency matrix A of the network, defined as Ai,j = 1 if nodes i and j are connected, and Ai,j = 0 otherwise. For all node pairs {n, m}, we compute the cosine similarity between their corresponding columns Ai,n and Ai,m, resulting in an (N × N) similarity matrix Sloc which serves as input to the dimensionality reduction step.

Importance layout

The importance layout reflects the similarity of nodes in terms of their network centralities1. Network centralities measure the importance of a particular node according to its position within the network. Numerous centrality measures have been proposed, and we incorporated four of the most widely used into a feature vector. For each node i we compute its (1) degree (the number of neighbors), (2) closeness (its average network distance to all other nodes), (3) betweenness (how often it acts as a bridge along the shortest path between two other nodes) and (4) eigenvector centrality (measuring its dynamic influence), resulting in a 4D vector ci. For all node pairs {n, m}, we then compute the cosine similarity between their corresponding vectors cn and cm, resulting in an (N × N) similarity matrix Scent, which serves as input to the dimensionality reduction step.

Functional layouts

Functional layouts can be used to display node similarities in terms of external features, such as the disease annotations of genes in Fig. 2b. For a given feature matrix F with Fi,j = 1 if node i is annotated to feature j, and Fi,j = 0 otherwise, we compute the cosine similarity between all node pairs {n, m} using the respective rows Fn,j and Fm,j, resulting in an (N × N) similarity matrix Sfunc, which serves as input to the dimensionality reduction step.

Combined layouts

Combined layouts allow for extrapolating between purely structural and functional layouts. We first construct a matrix with elements pi,j as in the global layout above, representing the structural aspect of the final layout. For each functional feature that we wish to include, for example annotations to different diseases, we then add an additional column containing the values Fi,j = 1 if node i is annotated to feature j, and Fi,j = 0 otherwise. These functional columns can now be scaled by a factor m ≥ 0, thereby modulating between purely structural layouts (m = 0) and layouts that are increasingly dominated by the functional annotations (m > 0). Finally, for all node pairs {n, m}, we compute the cosine similarity S(n, m) between their vectors pn and pm and collect the results into an (N × N) similarity matrix Scomb, which serves as input to the dimensionality reduction step of the pipeline.

Implementation

We used the Python package networkx25 to generate the model networks and compute the network properties required in the different layouts, such as adjacency matrices and node centralities. The force-directed layouts were generated using the Fruchterman–Reingold algorithm6 as implemented in NetworkX and igraph26, respectively, and using ForceAtlas227. Dimensionality reduction methods were implemented using the t-SNE24 and UMAP Python packages25, and the node2vec algorithm was implemented using the StellarGraph library28. Note that the implemented dimensionality reduction methods are not strictly deterministic, so that repeated calls may lead to slightly different outputs. To maximize the reproducibility, we therefore set a fixed random seed in the provided Python code.

To evaluate how well a particular layout algorithm reproduces network-based distances between nodes, we computed for all node pairs {n, m} the length of the respective shortest paths \({d}_{n,m}^{\rm{SP}}\) and their Euclidean distance \({d}_{n,m}^{\rm{Euc}}\) within the layout. The agreement between the two was then quantified using the Pearson correlation coefficient:

$${{r}} = {\frac{{\mathop {\sum}\limits_{\{ n,m\} } {({d}_{n,m}^{\rm{SP}} - {\mu }^{\rm{SP}})({d}_{n,m}^{\rm{Euc}} - {\mu }^{\rm{Euc}})} }}{{\sqrt {\mathop {\sum}\limits_{\{ n,m\} } {({d}_{n,m}^{\rm{SP}} - {\mu }^{\rm{SP}})^2} \mathop {\sum}\limits_{\{ n,m\} } {({d}_{n,m}^{\rm{Euc}} - {\mu }^{\rm{Euc}})^{2}} } }}}$$

where µSP and µEuc denote the respective mean values of network-based and Euclidean distances across all node pairs. We used the implementation contained in the numpy Python package29. Computational wall time was measured on computer hardware with a 2-GHz Quad-Core Intel Core i5 processor and 16 GB of RAM.