Abstract
The increase of carbon-dioxide-doubling-induced warming (climate sensitivity) in the latest climate models is primarily attributed to a larger extratropical cloud feedback. This is thought to be partly driven by a greater ratio of supercooled liquid-phase clouds to all clouds, termed liquid phase ratio. We use an instrument simulator approach to show that this ratio has increased in the latest climate models and is overestimated rather than underestimated as previously thought. In our analysis of multiple models, a greater ratio corresponds to stronger negative cloud feedback, in contradiction with single-model-based studies. We trace this unexpected result to a cloud feedback involving a shift from supercooled to warm clouds as climate warms, which corresponds to greater cloud amount and optical depth and weakens the extratropical cloud feedback. Better constraining this ratio in climate models – and thus this supercooled cloud feedback – impacts their climate sensitivities by up to 1 ˚C and reduces inter-model spread.
Similar content being viewed by others
Introduction
Cloud phase modulates reflected sunlight and affects projected warming
In response to climate warming, statistically more liquid phase clouds and fewer ice clouds are likely. For the same mass of condensate, liquid phase clouds are more reflective than ice clouds, and they tend to precipitate less efficiently. Since a warmer climate favors more liquid phase clouds, this implies that warming will lead to clouds with greater optical depth1,2,3 and spatial coverage1,2,3. As a result, the solar radiation reflected back to space would be greater, weakening the initial warming, a negative cloud feedback commonly referred to as the “cloud phase feedback”3,4,5. Although this feedback has not been explicitly characterized in climate models to date, it is hypothesized to substantially affect the strength of the negative cloud optical depth feedback and that of the negative cloud amount feedback to a lesser degree4,5 – two feedbacks that are well documented in Earth System Models (ESM). The magnitude of these two modeled feedbacks, while largely unconstrained by observations, is maximum in the extratropics, particularly over the Southern Ocean6,7,8,9. This is because mixed-phase temperatures, i.e., temperatures at which both liquid and ice can exist (0 ˚C > T \(\gtrsim\)−40 ˚C), are omnipresent in the troposphere at these latitudes. In addition to its connection to precipitation processes1,10, the optical depth feedback seems to depend on the presence of supercooled liquid relative to total cloud water at mixed-phase temperatures. The overall weakening of this negative feedback in the extratropics in present generation Coupled Model Intercomparison Project phase 6 (CMIP6) models relative to the previous CMIP5 models has contributed to increased CMIP6 equilibrium climate sensitivity9 (ECS) estimates (including their upper range)9, making them substantially larger than values derived from independent lines of evidence11,12.
Given the crucial role of supercooled clouds in projected warming, recent efforts have been devoted to evaluating cloud phase in ESMs and studying the relationship between Liquid Phase Ratio (LPR) and cloud feedback. Some studies have reported a link between increased liquid water mass relative to all condensed water (LPRmass) in the current climate and reduced negative optical depth feedback in individual ESMs13,14,15. Yet none have established a clear systematic relationship between current climate LPRmass and cloud optical depth feedback in CMIP models, nor have they explored a link with the cloud amount feedback. Additionally, it is unclear whether the LPRmass of CMIP6 models has increased compared to previous CMIP models and how it compares to observations. In this study, we address these research gaps by evaluating simulated LPR across CMIP generations using an instrument simulator and by analyzing how changes in LPR from CMIP5 to CMIP6 affect the weakening of the negative cloud feedback in the extratropics.
Constraining simulated cloud phase using observations
Earth system models (ESMs) use various methods to partition liquid and ice phases in clouds, from a simple temperature-based dependence16,17 to more sophisticated microphysical schemes18,19. For example, the temperature at which clouds are 50% liquid, 50% ice (i.e., LPRmass = 0.5; denoted T50/50; see Methods) – a metric often used to assess the fraction of supercooled clouds in ESMs – ranges from −1.6 to −32 ˚C (Fig. 1a). The lower T50/50 is in a model, the more supercooled clouds there will be relative to all clouds, and therefore, the larger its mean LPRmass. Several studies have consistently reported that older CMIP3 and CMIP5 models underestimate supercooled liquid clouds (too small LPRmass) compared to satellite observations7,20,21,22,23,24,25,26, which has led to considerable attention being paid to increasing LPRmass in the CMIP6 generation9,13,27,28,29.
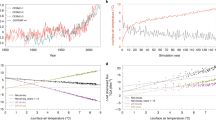
a Global mean of simulated mass LPR (LPRmass), computed as the ratio of the liquid water content to total water content in cloud, for seven CMIP3 (pink), ten CMIP5 (purple), and ten CMIP6 (red) models from the same modeling centers (see Supplementary Table 1–3). The dashed lines and shading represent the multimodel mean and spread (i.e., minimum and maximum), respectively. b Observed frequency, mass or hybrid LPR from different instruments and platforms: satellites in shading of black, fixed ground-based instruments in red and in situ aircraft measurements in blue (see Supplementary Table 4 and Supplementary Note 1). For clarity, no observations are shown at temperatures greater than 0 ˚C. In contrast with the models, it is not consistent to compare these observations among themselves (Supplementary Note 1). The insets show the temperature at which liquid clouds transition to ice clouds for all different models and observational datasets, expressed as the temperature at which clouds are 50% liquid and 50% ice (LPR = 0.5, noted T50/50). Note that for the CMIP3 models, only the T50/50 values are available from the literature (Supplementary Table 3), which are extrapolated to a narrow band along the 50/50 isoline.
Here we analyze for the first time global-scale outputs of a subset of CMIP models across three CMIP generations: ten CMIP6 models and their CMIP5 counterparts from the same modeling centers as well as seven CMIP3 models. A lack of required model outputs precludes us from studying all CMIP models. Yet, our model sample includes outputs from 10 modeling centers, which represent 8 of the 10 main ESM families – as classified by their model genealogy code following Kuma et al.30 – that participated in both CMIP5 and CMIP6. These 8 families account for about 95% of the total number of CMIP5 (60) and CMIP6 (101) models30 (Methods). Our results confirm that CMIP6 models simulate greater LPRmass than their predecessors, although the spread remains large (Fig. 1a).
Results
Given the underestimate of LPRmass reported in the literature7,20,21,22,23,24,25,26, one might reason that this increase of LPRmass in the models represents an improvement over the previous generations and surmise that their general increase in climate sensitivities is largely a consequence of that5,15. However, most CMIP5-based studies evaluated model LPRmass directly against observations7,20,23,24,25, which is not an optimal strategy for two important reasons. First, the definitions of cloud and LPR vary across observations and models, as discussed further below. Second, satellite instrument limitations require careful consideration when comparing to model outputs, though efforts were made to mitigate these discrepancies in previous work. In addition, the observed relationship between LPR and temperature can differ substantially depending on the instrument, platform (e.g., aircraft, ground-based or satellite), geographic region, cloud and LPR definitions, and type of clouds sampled, which has been shown in previous literature21,31,32,33 and is further exemplified in Fig. 1b. We note that, for the same reasons, it is not consistent to compare all these observational datasets to each other. For example, in situ aircraft measurements of mid-latitude and high-latitude clouds can indicate very little supercooled cloud at temperatures below −9 ˚C. This result contrasts with the larger LPRs from similar measurements targeting Arctic mixed-phase clouds (MPCs), which typically include both supercooled liquid and ice particles, or midlatitude ground-based remote-sensing observations. In polar regions, however, ground-based observations record a larger proportion of ice-dominated clouds – yet with large variability attributable to cloud phase definition – than at mid-latitudes. Overall, the global-scale satellite datasets report the greatest LPRs of all platforms, including Cloud-Aerosol Lidar and Infrared Pathfinder Satellite Observations (CALIPSO)-based datasets, which arguably correspond to the most reliable and complete global-scale cloud phase observations34,35,36. To complicate matters further, while the simulated LPRs are almost exclusively computed from mass concentrations of ice and liquid cloud water (LPRmass), observational analyses may use either LPRmass37,38, frequency of occurrence31,39,40,41 (LPRfreq), or a hybrid combination of frequency and volume of liquid and ice clouds42 (LPRhybrid).
A more observationally consistent framework for model evaluation
One way to account for observational limitations and enforce consistent cloud definitions, resolutions, and LPR methodology is to employ an instrument simulator. An instrument simulator mimics what a satellite-borne instrument would observe flying over an ESM atmosphere21,43 and its outputs can be compared directly to the observations that have been processed to be consistent with that specific instrument simulator. Consequently, one can evaluate the instrument simulator LPRfreq against the corresponding observed LPRfreq, defined as the ratio of liquid phase cloud fraction to the liquid plus ice cloud fraction. As a valuable extension beyond previous CMIP submissions, CALIPSO lidar simulator cloud phase outputs were requested for CMIP6 and 10 models provided them for the experiments that are relevant to this study. Here we take advantage of the resulting opportunity to evaluate cloud phase more consistently in these 10 models and constrain their LPRfreq against the compatible CALIPSO dataset31,35 using the simulator approach (Methods), which has not been done in with previous multimodel analyses. Using the lidar simulator increases diagnosed liquid-cloud occurrences and therefore shifts LPRfreq to cooler temperatures compared to LPRmass (Fig. 2), primarily because liquid droplets dominate the lidar signal21. Results indicate that 7 out of 10 CMIP6 models (Supplementary Table 1 and Supplementary Fig. 1) largely overestimate LPRfreq (Fig. 2), with their mean T50/50 being 5.8 ˚C less than in CALIPSO observations. Assuming that the effect of the lidar simulator found in the CMIP6 models is consistent across all CMIP generations (Methods), we infer a correspondingly smaller overestimate of LPRfreq in CMIP3 and CMIP5 models (Fig. 2).
Global mean of mass (as in Fig. 1a; dashed) and frequency (solid) LPR in CMIP models (red, purple and pink for ten CMIP6 and CMIP5 and seven CMIP3 models, respectively) against observed CALIPSO-GOCCP frequency LPR (as in Fig. 1b; Cesana et al.,31; solid grey). The simulated frequency LPRs are derived using a lidar simulator that uses cloud and cloud phase definitions and resolutions consistent with the observations as opposed to the mass LPRs, which are computed directly from the native climate model outputs (i.e., without a lidar simulator) and cannot be compared directly to the observations. Note that CMIP5 and CMIP3 multimodel frequency LPR datapoints are derived from mass LPR assuming a lidar effect similar to that in CMIP6 models. As in Fig. 1, the liquid-to-ice transition temperature (T50/50) is embedded for all curves with simulator (solid) and without simulator (dashed). The cooler this temperature is, the more supercooled clouds persist at cold temperatures. All CMIP model generations overestimate the amount of supercooled clouds at cool temperatures beyond the observational uncertainty (Supplementary Note 2).
Do CMIP models produce too many supercooled clouds or too few ice clouds?
Overall, the five models with prescribed temperature-dependent phase partitioning drive the multimodel bias while the five models with more complex microphysics are closer to the range of observational uncertainty, yet slightly biased in the opposite direction (Fig. 3a-b, Supplementary Fig. 1). This LPRfreq overestimate is mostly attributable to low- and mid-level clouds (at heights <7 km) in the extratropics and to high-level clouds (at heights ≥ 7 km) in the tropics (Fig. 3c-f, Supplementary Fig. 2). In the mixed-phase temperature range, CMIP6 models apparently simulate too many relative occurrences of liquid-dominated clouds (LPRfreq > 0.9) between −25 and 0 ˚C, too few ice-dominated clouds (LPRfreq <0.1) between −35 and −20 ˚C, and too many “mixed-phase” clouds (0.1 ≤ LPRfreq ≤ 0.9; Fig. 3a, b, Supplementary Fig. 1) at temperatures below −15 ˚C. In addition to these results, Figs. 3d and f help us conclude that the overestimate of liquid-bearing clouds is the main cause of the LPRfreq bias in the extratropics. We interpret the increase in supercooled clouds in CMIP6 models (Fig. 1a, Supplementary Fig. 2) as partly attributable to an increase of low-level cloud fraction44 to address the long-standing lack of low-level clouds in the tropics, subtropics and at midlatitudes35,45 but also as a consequence of modeling centers reducing “apparent” phase biases of CMIP5 models highlighted by the aforementioned studies7,20,23,24,25. Consistent with that hypothesis, when compared directly to our observed CALIPSO LPRfreq – that is, without a simulator, as done in many previous studies7,20,23,24,25 – the CMIP6 LPRmass comes close to the range of observational uncertainty whereas that of CMIP5 and CMIP3 models is largely an underestimate at all temperatures. That underestimation is even greater against a CALIPSO LPRhybrid estimate42 (T50/50 = −23.3 ˚C) often used in past studies to constrain cloud phase partitioning in ESMs7,46,47,48. We however note that although LPRfreq has increased in most models, generating larger negative (lower) T50/50, it has also decreased or remained unchanged in a few models (Fig. 4, Supplementary Table 1-2).
Global frequency of occurrences (%) of liquid phase ratio (LPRfreq) as a function of the temperature (°C) for a CALIPSO-GOCCP observations (2007-2016 Nighttime v2.9) and b the multimodel mean bias (model minus observations) of ten CMIP6 models using the lidar simulator. The black and red lines correspond to the mean frequency LPRfreq as shown in Fig. 2 for CALIPSO-GOCCP observations and the models, respectively. The dash-dotted and dotted red lines and the blue dash line correspond to temperature-dependent (n = 5) and complex-microphysics (n = 5) model means (Supplementary Table 1) and GISS-ModelE3 mean (n = 6), respectively. Zonal profiles of liquid (middle) and ice (bottom) cloud fractions for c, e CALIPSO-GOCCP and d, f the multimodel mean bias. The 0, −20 and −40 ˚C isotherms are represented in c–f. The T50/50 height transition for the multimodel mean is shown in solid purple in d and f, as well as its equivalent with observationally constrained liquid in dotted red and ice in dotted blue (effectively using observed liquid or ice cloud fraction instead of the simulated one). These isocontours show that most of the LPRfreq positive bias is driven by excessive liquid cloud fraction in the extratropics and excessive ice cloud fraction between roughly 20˚S and N.
a The difference in optical depth feedback9 from all clouds (W m−2 K−1) between the CMIP6 and CMIP5 versions of each modeling center (n = 10) as a function of the corresponding difference in T50/50 (˚C; from LPRmass, i.e., without lidar simulator). b Same as a but for the amount feedback. c Same as a but for the total cloud feedback. Negative ∆T50/50 and positive ∆feedback correspond to increased LPRmass (likely more supercooled clouds) and increased cloud feedback (stronger positive or weaker negative) in CMIP6 models compared to their CMIP5 counterparts. d Actual total cloud feedback of GISS-ModelE3 as a function of actual T50/50 (from LPRmass, i.e., without lidar simulator) for the six different model configurations as well as the mean of the two coolest and warmest T50/50 configurations. The shading corresponds to the global cloud feedback. All correlations except that shown in panel a are statistically significant (with probability p < 0.05).
Although the overestimate of supercooled clouds causes most of the LPRfreq bias, we expect that the underestimate of ice-dominated clouds (LPRfreq <0.1), the other contributor to the bias, could be mitigated to at least some degree by accounting for large hydrometeors (classified as precipitation) based on previous findings49. Currently, most modeling centers (eight CMIP6 models out of the ten used in Fig. 2) have opted to neglect their effect on radiation49, which means that they are not accounted for in simulated Earth’s energy budget and, because they are radiatively inactive, any instrument simulator is therefore consistently blind to them by convention. Making radiation schemes and any simulator instrument aware of precipitation may substantially affect LPRmass, LPRfreq and cloud feedback50,51. By increasing the amount of ice-dominated clouds, including precipitation can push T50/50 toward higher temperatures, by 3 to 12 ˚C depending on the ESM50 (Supplementary Fig. 3). We posit that models’ cloud phase representation should be evaluated using a consistent evaluation framework, via comparison of cloud frequencies estimated from the lidar simulator to their equivalent observed quantities. Additionally, rather than relying solely on LPRfreq, liquid and ice cloud fractions should be also analyzed separately. Finally, the radiative effect of precipitation particles should be included in ESMs’ radiation schemes to further improve consistency with observations from a microphysics and radiative perspective.
Impact of modifying LPR on climate projections
While the overall consequences of this evolving increase in supercooled clouds over CMIP generations are varied, there is no doubt that the increases affect the response of simulated clouds to climate warming (i.e., cloud feedback). Past studies6,7,9,15 have suggested a link between LPRmass or liquid water content (LWC) and weakened negative cloud feedback in some individual models, but to our knowledge none have demonstrated it systematically across many CMIP models. To establish that connection here, we use T50/50 derived from LPRmass – a proxy for the amount of supercooled clouds – and the shortwave (SW) cloud optical depth feedback (Methods). We also focus our analysis over the extratropics (55˚ to 75˚ latitude in both hemispheres), where the change between CMIP6 and CMIP5 cloud feedback is large (Supplementary Fig. 4) and the impact of cloud phase changes on cloud feedback is maximum6,7,8,9. To better isolate this impact, we further characterize the change in cloud feedback as a function of the change in T50/50 between CMIP6 and CMIP5 climate models from each modeling center (Fig. 4; CMIP6 minus CMIP5, Methods). Our results reveal that increasing LPRmass in any climate model (lower T50/50, going to the left on Fig. 4a) is somewhat correlated with increased optical depth feedback (weaker negative or stronger positive, going up on Fig. 4a; linear correlation coefficient r = −0.29). Although that relationship is not statistically significant and is driven by only a few models, it becomes stronger when only low-level clouds are considered (Supplementary Fig. 5, r = −0.51), yet still not statistically significant. Such results also suggest that the relationship between present-day LPRmass and the so-called negative cloud phase feedback52, an increase of liquid clouds at the expense of ice clouds in a warmer climate, 52is only happening in some models. In these models, the greater LPRmass (i.e., more liquid clouds with respect to all clouds), the weaker the negative cloud phase feedback and its contribution to the optical depth feedback, because fewer ice clouds are in effect being replaced by liquid clouds in a warmer climate. More surprisingly, greater LPRmass (lower T50/50, going to the left on Fig. 4b) also corresponds to a decrease of the cloud amount feedback (less positive or more negative, going down on Fig. 4b) – further elucidated in the next paragraph – at a rate that more than offsets the optical depth feedback increase (Fig. 4b). This dominance of the cloud amount feedback change over the optical depth feedback change explains why the extratropical SW cloud feedback change is also negatively correlated with greater LPRmass (Fig. 4c).
Yet the extratropical CMIP6 cloud amount feedback is larger than in CMIP5 models, despite their overall increased LPRmass. This counter-intuitive result suggests that other changes between CMIP5 and 6 model versions have contributed to increasing the cloud amount feedback, which is consistent with the large positive intercept of the correlation line between ∆cloud amount feedback and ∆ T50/50 (Fig. 4c). Part of this change is likely attributable to substantial developments in boundary layer and cloud parameterizations to reduce low cloud biases, which, in turn modified cloud sensitivities to climate change9,53. Ultimately, this increase has masked the negative contribution of greater LPRmass to the cloud amount feedback.
To further investigate these unexpected results and better isolate the effect of LPR on cloud feedback, we analyze outputs from six configurations of the NASA Goddard Institute for Space Studies ModelE3 (GISS-ModelE350). The GISS-ModelE3 model is well-suited for this analysis because it employs a state-of-the-art treatment of stratiform cloud microphysics (including prognostic precipitation, which is included in radiation and instrument simulators; Methods) which leads to realistic supercooled and mixed-phase clouds50 (Fig. 3b). It also provides a variety of possible T50/50 and LPRfreq distributions50 (Supplementary Fig. 3). Finally, its cloud phase changes in response to warming shows the same shift from supercooled to warm clouds and little to no changes in ice clouds as in the CMIP6 multimodel mean (Fig. 5).
Vertical temperature profiles (in ˚C) of future a ice and b liquid cloud fraction changes (a, b; CF in %) in response to a uniform 4 K surface temperature increase (AMIP4K – AMIP) as simulated by the six GISS-ModelE3 configurations (blue line) and by CanESM5, CESM2, CNRM-CM6-1, GFDL-CM4, IPSL-CM6A-LR and MRI-ESM2 using a lidar simulator over the extratropics. c, d Same as a, b but for their raw water content (gkg−1). Note that we use the only six CMIP6 models that provided the AMIP4K simulator outputs in a and b, but we also show the full ten-model sample in c and d (dotted red line), for which the results are very similar to the 6-model sample (red line). The shading corresponds to plus or minus one standard deviation.
Using these six configurations of the same model with diverse tuning strategies, we find that greater GISS-ModelE3 LPRmass in present-day climate generates greater amount and liquid water content from all clouds in response to warming and, in turn, a stronger negative cloud amount feedback – consistent with CMIP models (Fig. 4) – and optical depth feedback (Supplementary Fig. 6). Some part of the supercooled liquid cloud population, which can produce both liquid and frozen precipitation, are replaced by warm liquid clouds in response to warming (Fig. 5), which can only produce liquid precipitation. Warm liquid clouds form precipitation less readily than their supercooled counterparts54, leaving more atmospheric moisture and thus greater cloud amount and water content compared to present-day climate (Fig. 5). Such an increase in liquid cloud amount and optical depth generates more SW reflection in a warmer climate, thereby producing a negative cloud feedback, as illustrated in Fig. 6. In the literature, a similar mechanism has been documented involving ice clouds being replaced by warm liquid clouds, sometimes referred to as cloud lifetime feedback1. Here we find evidence in GISS-ModelE3 and in CMIP6 models that the change in cloud amount and water content mostly results from a shift of supercooled clouds to warm clouds rather than of ice clouds to supercooled or warm clouds (Fig. 5). This finding profoundly advances understanding of the cloud phase feedback, which was previously hypothesized to be mostly driven by ice-containing clouds being effectively replaced by warm clouds in response to global warming. Thus, adding supercooled clouds in the present-day climate, which is equivalent to increasing LPR, strengthens the increase of liquid cloud amount and liquid water content in response to warming (Fig. 5 and Supplementary Fig. 7, mostly from warm liquid clouds) and its associated negative feedback (Fig. 4 and Supplementary Fig. 8). This supercooled cloud feedback and the fact that LPR (via supercooled cloud amount) increased between CMIP5 and CMIP6 models likely explains the correlation between increased LPRmass and stronger negative cloud amount feedback in CMIP models (Fig. 4).
Response of present-day liquid cloud (left) to warming (right) CMIP6 models. We note that other feedbacks may occur and are not represented here. Instead, we focus on the so-called supercooled cloud feedback, which occurs in parts of supercooled clouds. These clouds become less precipitation-efficient warm clouds in response to warming, which contributes to increasing the overall liquid cloud amount and optical thickness in the future climate, and therefore their reflection, constituting a negative feedback.
We note that precipitation efficiency changes between CMIP generations could also influence this feedback2 although we do not know to what extent: a greater precipitation efficiency in CMIP6 models would weaken it whereas a reduction would strengthen it. However, in order to achieve greater amount of liquid clouds in the present-day climate, one may speculate that some modeling centers have lowered the precipitation efficiency in their CMIP6 models, which is consistent with the surface precipitation rate per amount of low-cloud cover in CMIP6 models being smaller than that of CMIP5 (not shown).
In GISS-ModelE3 the negative optical depth feedback averaged over all clouds strengthens as present-day LPRmass increases (Supplementary Fig. 6), while it can go either way in CMIP models5,13,14,15 (Fig. 4). Conventional wisdom tells us that the increase in extratropical cloud optical depth in response to warming is mainly controlled by two mechanisms in climate models: a cloud phase shift of ice to warm liquid clouds, and a shift of the moist adiabat to higher temperatures, which allows greater LWC to be sustained55, mostly at supercooled temperatures, and is often referred to as an “adiabat feedback”. Neither of these can be computed at this time, making it difficult to quantify their contribution to cloud optical depth changes5,13,14,15. However, here we reveal a shift from supercooled to warm clouds, a largely overlooked mechanism (Fig. 6) that has never been characterized before. This shift contributes greatly to strengthening not only the negative cloud amount feedback, but also the negative optical depth feedback, because warm clouds are less precipitation-efficient than supercooled clouds and therefore sustain greater water content. Furthermore, we find that the ice to liquid phase shift is very small in the six configurations of GISS-ModelE3 and the multimodel mean of the CMIP6 ESMs (Fig. 5), in agreement with observations (Supplementary Fig. 9), but contradicting previous understanding based on studies using a single ESM.
As a result, the extratropical SW cloud feedback of the two GISS-ModelE3 configurations with the warmest transition from liquid to ice (T50/50 = −9.1 ˚C: fewer supercooled clouds and smaller LPRmass) is one third larger (i.e., less negative) compared to that of the two configurations with the coolest transition (−15 ˚C: more supercooled clouds and greater LPRmass; Fig. 4d). All else being equal, such a difference in T50/50 (from LPRmass) is of the same order of magnitude as the CMIP6 model negative bias (∆T50/50 = −5.8 ˚C, from LPRfreq) and could generate a similar feedback change in some CMIP6 models, should their LPRmass be decreased to correct LPRfreq bias and match the observational constraint.
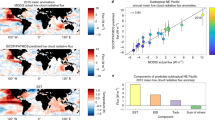
Predicting the overall effect of recalibrating CMIP6 supercooled clouds on cloud feedback is difficult because, going from CMIP5 to CMIP6, myriad changes were implemented in model parametrizations that affected cloud feedbacks. However, we postulate that reducing LPRmass to correct this LPRfreq bias would generate a strengthening of the positive cloud amount feedback averaged over all clouds. This more positive cloud feedback could be slightly compensated by a stronger negative optical depth feedback in some models but would most likely be enhanced by a weakening of the negative optical depth feedback, given our findings based on GISS-ModelE3 and CMIP6 models (Fig. 5). Ultimately, this correction would result in a less negative or more positive extratropical SW cloud feedback (Methods), according to our sample of CMIP models, which is representative of an even larger sample of them in terms of feedback signs and changes (Supplementary Fig. 4). We further utilize the relationship between CMIP6 ECS and the lidar simulator T50/50 to assess the effect of correcting T50/50 on simulated ECS, based on our observational constraint and using a direct constraint approach53,56. Doing so may affect the ECS by at least 0.5 ˚C in half of the models used in this study (from −0.6 ˚C to +1 ˚C; Supplementary Table 5). More importantly, it consistently decreases the multimodel ECS standard deviation in both the CMIP6 models and GISS-ModelE3 configurations (by up to more than a factor of 2), using both the aforementioned direct constraint and a more traditional “emergent constraint” approach53,57,58 (Methods, Fig. 7). Although this effect is model dependent, such results further illustrate that better constraining the cloud phase representation in CMIP6 models would result in reduced ECS inter-model spread, by bringing some convergence to one part of the cloud feedback uncertainty.
a effect of correcting the lidar T50/50 bias to match the observational constraint in CMIP6 models, in which the arrows indicate the correction and the open circles the corrected values. GISS-ModelE3 Phys (the configuration with the most realistic cloud phase partitioning50) is also used in this CMIP6 regression. b same as a using the emergent constraint method. c and d, same as a and b, respectively, but for GISS-ModelE3. Three GISS-ModelE3 configurations are not corrected in c because they fall within the observational uncertainty range (Tun1, Tun5 and Phys, Supplementary Table 6). The black and grey solid circles correspond to the original and constrained mean ECS, respectively, within plus or minus one standard deviation (height of error bar).
Conclusions
Compared to early climate models, the representation of cloud phase has greatly improved18,59, partly driven by increased understanding of mixed-phase cloud processes and by the availability of more accurate and comprehensive cloud phase observations60. In the present study, we analyze how well three CMIP generations of climate models represent the cloud phase using a simulator approach and then we investigate how changes in cloud phase between CMIP generations have affected extratropical cloud feedback. We find three notable results, the first two of which contradict previous understanding:
-
(1)
The average liquid phase ratio is overestimated in all CMIP generations, based on a consistent comparison to observations using a simulator approach, and even more so in the latest generation (CMIP6). Compared to CALIPSO observations, the CMIP6 liquid-to-ice transition temperature T50/50 is too low in 7 out of 10 models, and by 5.8 ˚C in the multimodel mean, which is 3.3 ˚C worse than the earlier models of CMIP5. This unexpected result may have been induced by past inconsistent evaluations of ESM cloud phase against observations7,20,23,24,25, which suggested a LPR underestimate of CMIP5 and CMIP3 models and very likely prompted a strong LPR increase in CMIP6 model development.
-
(2)
Although other cloud feedback processes can impact extratropical cloud feedback in CMIP models1,10,53, our results indicate that cloud phase partitioning changes can substantially modify this feedback. In particular, the surprising correlation between reduced LPR and increased cloud feedback in CMIP models is mainly explained by the weakening of the negative “supercooled cloud feedback”, an undocumented feedback that emerges from a shift of supercooled clouds to warm liquid clouds, as revealed by our GISS-ModelE3 and CMIP6 analysis. Although we do not have the data to verify that this shift happens in all CMIP6 models, we do provide evidence for the existence of a supercooled cloud feedback within a solid framework. As done in previous cloud phase studies1,3,15, we first demonstrate it using a relevant ESM (as explained further below) in conjunction with an explanation of the mechanism: in response to warming, part of the supercooled liquid cloud population in effect become less readily precipitating warm liquid clouds (Fig. 5). We then show further evidence from both CMIP models and observations (Fig. 5, Supplementary Figs. 7 and 9, and Supplementary Note 3), which also suggests that liquid clouds tend to be more frequent and – in some models – to have a larger optical depth in a warmer climate, resulting in a negative cloud feedback.
-
(3)
Constraining T50/50 in climate models strongly impacts their ECS (by up to 1 ˚C) and may substantially reduce the ECS uncertainty in our 10-model CMIP6 and 6-configuration GISS-ModelE3 ensembles (Fig. 7, by up to a factor of 2), using two different methods. Such a result provides evidence that improving observational constraints on model LPR would reduce the uncertainty in climate projections. For that purpose, meaningful cloud phase evaluation requires a methodologically sound framework, such as comparison of cloud frequencies from a lidar simulator to lidar-observed quantities. Furthermore, precipitation (especially ice phase) should be included in radiative transfer as well as in in lidar simulator calculations owing to its contribution to LPRfreq. Finally, rather than relying solely on LPRfreq (or T50/50), it is also recommended that liquid and ice cloud fractions also be separately evaluated.
Methods
Computation of LPR and temperature at which clouds are 50% liquid, 50% ice, T50/50
Definitions of different LPRs. Throughout the manuscript, we compute the liquid phase ratio, which ranges between 0 and 1, as the ratio of the liquid cloud water or fraction to the sum of the liquid and ice cloud water or fraction in each longitude, latitude and altitude gridbox and for each time step. Thus, LPR = 1 or 0 correspond to gridboxes that are purely liquid or ice clouds, respectively, and a mixture of both cloud phases for values in between. For the LPRmass, directly computed from model’s raw outputs without using a satellite simulator, we use profiles of ice and liquid water contents (referred to as “cli” and “clw”) monthly files downloaded from the earth system grid federation (ESGF) website, which hosts the official CMIP archive, for present-day Atmospheric model intercomparison project (AMIP) simulations, which correspond to sea surface temperature (SST) prescribed runs. For the CALIPSO simulator outputs, we use profiles of the lidar simulator liquid and ice cloud fraction monthly files (referred to as “clcalipsoliq” and “clcalipsoice”) for the same AMIP simulations, which includes day and nighttime data. In both cases, we use the last eight years of the AMIP simulations to get a similar annual variability as in the observations – and because it partially overlaps with the observational record for CMIP6 models – and we exclude gridboxes that are not sampled by the satellite (latitudes poleward of 82˚ N and S).
Computation of LPR-temperature relationship. To compute the LPR-temperature relationships, we derive LPR profiles as a function of the temperature, for 3 ˚C bins from −93 ˚C to 21 ˚C rather than altitude or pressure grids. For the raw model outputs, we directly use the temperature profiles that are available on the same pressure levels as the liquid and ice cloud water contents, or we linearly interpolate them if on different levels. For the CALIPSO simulator variables, which are given on the satellite altitude levels, we convert the temperature from pressure levels to the satellite altitude levels and then derive LPR profiles as a function of the temperature using 3 ˚C bin increments. In some models, there might be LPR greater than 0 at temperatures below −40 ˚C because we use monthly mean profiles of temperatures (and water content or cloud fraction), which are averaged over smaller time scales, where temperatures can sometimes be greater than −40 ˚C and coincide with the presence of liquid clouds. For the observations, the liquid and ice temperature profiles for the same 3 ˚C bins are available in monthly mean files for the 2007−2016 period on the General Circulation Models (GCM)-Oriented CALIPSO Cloud Product (CALIPSO-GOCCP) website (v2.9). We then interpolate all the model files onto the same 2.5˚ × 2.5˚longitude-latitude grid as the observations and further average them along each dimension to obtain 38-interval temperature-LPR arrays. Finally, we select the two data points on either side of LPR = 0.5 and interpolate them linearly at LPR = 0.5 to derive the corresponding temperature, termed T50/50.
Definition of the liquid-to-ice transition T50/50. In this study, we employ T50/50 because it conveniently characterizes the transition between liquid- and ice-dominated clouds, it has been widely used to assess the fraction of supercooled clouds in the literature, and it can be utilized to compare models with observations using the lidar simulator. To address the fact that T50/50 only represents the transition temperature between liquid- and ice-dominated clouds and may not capture the full variability of LPR over a large range of temperature, we have designed an additional metric defined as 1 minus the mean of the LPR between −40 and 0 ˚C. We have reproduced our computations for Fig. 4 and have found similar results and conclusions (not shown). We show an example in Supplementary Fig. 6 using GISS-ModelE3. Thus, we have used T50/50 in the mean manuscript for simplicity.
Choice of CMIP models
Our choice of models is constrained by the availability of model outputs that are needed for our computations, as is often the case in multimodel comparison exercises. For all our results but Fig. 5, we used ESMs from the 10 modeling centers that provided ice and liquid water content, liquid and ice CALIPSO-simulator profiles, temperatures and geopotential heights for the AMIP experiment, as well as the necessary outputs to compute cloud feedbacks (described in the “Cloud feedback computations” section below) for both their CMIP5 and CMIP6 model versions. This number is mostly constrained by the CALIPSO-simulator outputs availability. While it may seem small, it is on the higher end of the spectrum when it comes to multimodel evaluation analyses, judging from recent simulator-oriented studies44,53,61,62. Furthermore, there are 10 main ESM families that have participated in both CMIP5 and CMIP6 according to the classification used by Kuma et al.30 (their Fig. 1 and Supplementary Table 1), which is based on model genealogy code. Our sample of 10 models includes outputs from 8 of these 10 main ESM30, which account for about 95% of the total number of CMIP5 and CMIP6 models (161). And finally, as mentioned in the main manuscript, various ways of simulating cloud phase are represented in our subset of models, from a simple temperature-based dependence16,17 to more sophisticated microphysical schemes18,19.
Simulator approach and comparison with CALIPSO-GOCCP
To ensure a fair evaluation that accounts for the CALIPSO lidar limitations and uses similar cloud and cloud phase definitions and resolutions as in the observations, we use the CALIPSO-like outputs from CMIP6 models, obtained through the use of a CALIPSO lidar simulator21, to compare with the General Circulation Model-Oriented CALIPSO Cloud Product (CALIPSO-GOCCP31,35, v2.9). The lidar simulator computes lidar attenuated backscatter profiles using temperature, pressure, and water content and effective radius of cloud particles63. A stochastic subcolumn generator is also used to characterize subgrid-scale variability and accounts for the model-specific overlap assumptions64. Then, liquid- and ice-dominated cloudy subgrid-pixels are distinguished using a method consistent with the observations. It is important to keep in mind that this cloud phase diagnostic characterizes the frequency of occurrence of liquid and ice clouds, which is very different from their mass, partly explaining why the LPRmass and LPRfreq are different, in addition to using different sampling and cloud definitions. Note that we exclude latitudes poleward of 82˚ N and S to be consistent with observations.
CALIPSO-GOCCP cloud phase
In this study, we use CALIPSO-GOCCP31,35 (2007-2016, v2.9) for multiple reasons. First, CALIPSO-GOCCP is the only dataset that has a simulator counterpart available in the models we selected together with corresponding profiles of temperature and water phase in the “raw” model output (i.e., without simulator): ta, cli and clw. This makes it the best choice for consistent comparisons of model and observations (i.e., using same cloud and cloud phase definitions, sampling, and resolutions) and to assess the effect of the simulator on the raw output. Second, CALIPSO-GOCCP is arguably the most accurate global-scale cloud phase dataset available (e.g., Cesana et al.31). CALIPSO-GOCCP documents cloud properties every 333 m along-track-resolution near-nadir lidar profiles for 480 m height intervals. Instead of relying on temperature, the cloud phase is diagnosed based on cloud properties (including particle shape, as described next) and for multiple levels, in contrast with passive sensors. More specifically, liquid- and ice-dominated clouds are distinguished using the polarization state of the laser signal, which changes when backscattered by a non-spherical crystal contrary to spherical droplets. Additionally, undefined-phase clouds are diagnosed below highly reflective layers when the distinction between the two water phases is hampered by multiple scattering and noise. We focus on nighttime observations to reduce the influence of noise, induced by solar photons, on the cloud phase diagnostic. The effect of using nighttime observations instead of day and nighttime observations on the cloud fraction is marginal (less than +/− 1.2% in zonal cloud profiles, not shown) compared to the large model-to-observations biases (on the order of +/− 10%35). To estimate the potential effect of using only nighttime observations on cloud phase diagnostics, we have run a GISS-ModelE3 simulation using nighttime only (based on solar illumination) and compared the results with the regular simulation using day and nighttime. We have found no significant differences between the two simulations in the GCM diagnostics related to cloud phase, which we evaluate with observations in the study (not shown). We note that in situ and ground-based remote-sensing datasets, while very useful, are also not representative of global scale observations, which make them less relevant for global or even semi-global scale studies. Finally, CALIPSO-GOCCP v3.1.2, which is the same as v2.9 but with the addition of opacity diagnostics, is used in Supplementary Fig. 9e.
Lidar simulator effect: Estimating LPRfreq from LPRmass in CMIP5 and CMIP3 models
The CALIPSO simulator cloud phase outputs were not requested for CMIP5 and did not exist when CMIP3 was undertaken. As a result, only a few CMIP5 models implemented and used the CALIPSO simulator cloud phase module in their models, but none made their results publicly available. To address this shortcoming, we assume that the effect of the CALIPSO simulator on CMIP6 raw LPR (LPRmass) is similar across CMIP generations, when applied to multimodel means. We compute the difference between the multimodel CMIP6 LPRmass and CALIPSO-simulator LPRfreq curves (i.e., the difference between the dashed and solid red lines in Fig. 2) at all temperatures, which corresponds to a “lidar effect” that effectively transforms LPRmass into LPRfreq. We then subtract this lidar effect from the multimodel CMIP5 LPRmass (i.e., the solid purple line in Fig. 2) at all temperatures to obtain LPRfreq. Similarly, we compute the lidar effect using T50/50. Based on ten CMIP6 models, we find a lidar effect of −8.9 ˚C at T50/50.
To assess the validity of our assumption, i.e., the effect of the lidar simulator is similar across CMIP generations, we compare this effect in a sample of four CMIP6 models (CESM2, CanESM5, CNRM-CM6-1 and IPSL-CM6A-LR) and their CMIP5 equivalents (CAM5, Can4, CNRM5 and IPSL5B, not shown), which were obtained by the lead author GC during past research. The lidar effect in CMIP5 models (−6.8 ˚C) is only 1.1 ˚C warmer than the effect using the same four CMIP6 models (−7.9 ˚C), which confirms that our assumption is reasonable. Assuming that the lidar effect is greater in all nine CMIP5 models by 1.1 ˚C (e.g., −7.8 ˚C instead of −8.9 ˚C) would not qualitatively change our results. The CMIP5 models would still be less biased than the CMIP6 models compared to CALIPSO-GOCCP. We note that even if this assumption was wrong, it would not affect the main conclusions of this study in any capacity since we only use it to evaluate CMIP5 and CMIP3 models in Fig. 2 for reference purposes. Because liquid and ice water contents were not requested for CMIP3, we lack information regarding LPRmass dependency on temperature for the CMIP3 models. Therefore, we only apply this method to their T50/50, which were either obtained from the literature directly or computed based on their cloud phase parameterization descriptions in the literature (Supplementary Table 3).
Cloud feedback computations
The radiative response of clouds to climate warming, referred to as cloud feedback, used in this study is the same as in Zelinka et al.9. In that study, they characterize the atmospheric contributions to cloud feedbacks by using model outputs from the CMIP database in which the atmospheric CO2 levels were quadrupled (4xCO2 simulation) compared to a pre-industrial atmosphere (piControl simulation). Then, the cloud feedback is computed using radiative kernels that quantify the sensitivity of top-of-the-atmosphere radiation to small perturbations and is then adjusted for non-cloud influences65. Finally, the SW component is further decomposed into the amount, scattering and absorption sub-components using the approximate partial radiative perturbation (APRP) technique66. Because the absorption component is very small compared to the scattering, we treat the scattering component as the sum of the scattering and absorption components. This feedback is very similar to the broadly used optical depth feedback (Zelinka et al.67, their Supplementary Fig. 1), which is the term we use to refer to our scattering feedback throughout the manuscript. More details are provided by Zelinka et al.9. We use the 4xCO2-derived feedbacks rather than that from a uniform SST warming of 4 K not only because the required model outputs are available but also because the future SST warming pattern that corresponds to 4xCO2-derived feedback is in principle more physically plausible. A recent study pointed out that on average, feedbacks computed via both routes are very similar and show equivalent spread68.
For GISS-ModelE3, we quantify cloud feedbacks using simulations lacking a coupled ocean model as opposed to fully coupled simulations in CMIP6 models68. Additionally, we apply the cloud radiative kernel method69, which is more computationally efficient, allows a finer decomposition of the feedback components and produces values that are very similar to the radiative kernel method in terms of magnitude and sign in the extratropics (Zelinka et al.70, their Fig. 5 and Zelinka et al.67). We do not use this cloud radiative kernel method with CMIP6 and CMIP5 models because the necessary variables are missing for most CMIP6 models. The resulting cloud feedback is decomposed into amount, altitude, optical depth, and residual contributions. The amount, altitude and optical depth contributions quantify the feedback generated by changes in cloud fraction, altitude and optical depth, respectively, while keeping the other two parameters constant in the cloud top pressure and optical depth ISCCP bin space. We characterize the atmospheric contributions to cloud feedbacks by prescribing the SST in the control simulation, based on monthly observations, and by applying a uniform warming of 4 K in the perturbed simulation. See Zelinka et al.70 and Cesana et al.50 for more details.
Finally, we focus on SW feedbacks in this study because changes in cloud phase have a strong impact on SW radiation and because most of the intermodel spread in CMIP cloud feedback comes from the SW component, as explained in the abstract and introduction, and shown in previous studies. Changes in cloud phase may also affect LW radiation – although we do not find consistent correlations between LW feedback and T50/50 changes in CMIP models and GISS-ModelE3 (not shown) – and other feedbacks, which we do not investigate here.
Changes between CMIP models within modeling centers (used in Fig. 4a–c and Supplementary Fig. 10)
We focus our analysis over the extratropics (55˚S/N to 75˚S/N), where the change between CMIP6 and CMIP5 cloud feedback is large (Supplementary Fig. 4) and the impact of cloud phase changes on cloud feedback, particularly its optical depth component, is maximum6,7,8,9. Yet we do not find meaningful correlation between T50/50 and the optical depth feedback from low-level or all clouds (Supplementary Fig. 11) in part because of differences of cloud properties other than phase in the ESM mean states that impact the optical depth feedback. Such differences are greater between ESMs from different modeling centers, which use various parameterizations, radiative schemes, dynamical cores and resolutions, than among CMIP versions within the same modeling centers, for which changes are more incremental. To better isolate the impact of the cloud phase on the simulated optical depth feedback, we therefore characterize the change in optical depth feedback from all clouds as a function of the change in T50/50 between CMIP6 and CMIP5 climate models from each modeling center (Fig. 4a). For that, we picked CMIP5 and CMIP6 models from the same modeling centers, as listed in Supplementary Tables 1 and 2, and computed differences between CMIP6 and CMIP5 cloud feedback and T50/50. The T50/50 values are computed as explained above and the cloud feedbacks are fully described by Zelinka et al.9. We use the same method for Fig. 4b, c and Supplementary Fig. 10.
Choice of NASA GISS-ModelE3 outputs
As done in previous studies1,3,15, we use a specific yet relevant ESM in conjunction with providing a physical explanation and further evidence from the multimodel analysis to further dissect the relationship between cloud phase and cloud feedback. We analyze outputs of six configurations of the NASA GISS-ModelE3 ESM (including four configurations similar to that used by Cesana et al.50, Tun1-3 and Phys, and two additional configurations designated Tun 4 and Tun 5), in which only cloud-related parameters are varied and not parameterization physics. They represent “equally-likely” physics representations that were primarily obtained by applying machine learning methods to roughly 40 uncertain cloud-related parameters to optimize agreement with satellite observables. The primary structural difference between the Phys configuration and the Tun1-5 configurations is an alternative formulation for convective entrainment. GISS-ModelE3 is a relevant choice for three main reasons. First, it simulates complex microphysical processes necessary to produce realistic supercooled and mixed-phase clouds (including prognostic precipitation) that are in surprisingly good agreement with observations, both on a global scale and at the process level50,71. Second, it offers a variety of possible T50/50 values – and therefore LPR distributions – from its six configurations that use different sets of cloud-related tuning parameters (Supplementary Fig. 3). Third, the liquid and ice cloud fraction changes in response to warming are very similar to the CMIP6 multimodel mean (Fig. 5).
In GISS-ModelE3, the stratiform cloud microphysics treatment is based on a modified two-moment microphysics scheme with prognostic precipitation18, in which cloud water and ice, rain, and snow mixing ratios and number concentrations are prognostic variables. Rain and snow both require other hydrometeors to already exist, unlike cloud droplets, which form via aerosol activation, and cloud ice, which can form from aerosol and cloud droplet freezing, homogeneously and heterogeneously. Typically, snow and rain hydrometeors are larger and fall faster than cloud particles. Finally, the cumulus category realized for a given environment is a function of dynamically determined entrainment and its cloud phase is based on a temperature threshold. Compared to the original scheme18, the GISS-ModelE3 configuration used here includes the following updates pertinent to our findings: depositional growth of stratiform snow is included; the Bergeron process is simulated through the different saturation vapor pressures over ice and water as in nature, rather than using the Bergeron enhancement of the original two-moment microphysics scheme, which transfers water directly from cloud droplets to cloud ice; at supercooled temperatures warmer than homogeneous freezing of liquid drops, heterogeneous ice nucleation occurs only in the immersion mode, using the temperature dependence of Demott et al.72. The cloud phase treatment in the moist convection scheme – described in detail in Cesana et al.50 – is based on a temperature threshold varying from 251 K to 261 K depending on the configuration. We note that the moist convection cloud phase has a relatively small impact on the overall cloud phase representation in GISS-ModelE3.
Each configuration of GISS-ModelE3 uses a different combination of tuning parameters and therefore it is difficult to pinpoint with precision what causes changes in the LPR and whether these changes affect cloud feedback. To better isolate the impact of LPR on cloud feedback, we perform two sensitivity tests where we reduce and increase LPR in the GISS-ModelE3 configurations with the greatest (Tun2) and smallest (Tun1) LPR, respectively, by tweaking a single tuning parameter. This parameter increases the speed of a few microphysical processes such as autoconversion, immersion freezing and accretion, which only affect the liquid cloud amount (Supplementary Fig. 7). We then compare the initial tuning configurations of GISS-ModelE3 with their modified counterparts, Tun2 LPR- (smaller LPR, fewer liquid clouds than Tun2) and Tun1 LPR+ (greater LPR, greater liquid clouds than Tun1), to estimate the impact of LPR changes on liquid and ice cloud fraction and cloud fraction changes as well as cloud feedback. We find that greater LPR in present-day climate by virtue of increasing liquid cloud fraction generates greater cloud amount (Supplementary Fig. 7) and water content increase in response to warming and, in turn, a more negative cloud amount and optical depth feedback (Supplementary Fig. 8). This increase is contributed almost exclusively by liquid clouds while ice clouds are fairly insensitive to changes in LPRfreq (Supplementary Fig. 7). In addition, we note that the amount and change of ice clouds is fairly small compared to that of liquid clouds, below 2 km, suggesting that cloud phase feedback is probably also small.
Cloud feedback estimates resulting from the LPR observational constraint
Here we analyze the possible outcomes of re-tuning T50/50 to smaller or greater temperatures in CMIP6 models to match our observational constraint. Collectively, CMIP6 models underestimate T50/50 by 5.8 ˚C. On the one hand, increasing T50/50 to greater temperatures (thereby reducing supercooled clouds) would strengthen the magnitude of the multimodel mean negative low-level cloud optical depth feedback over these latitudes by −0.06 Wm−2K−1 based on the slope of the linear fit (Fig. 4a, −0.01 Wm−2 K−1 per K), making it marginally more negative than that of CMIP5 models (−0.15 Wm−2 K−1; Supplementary Table 2). On the other hand, the cloud amount feedback from all clouds would increase by 0.12 Wm−2K−1, at a rate that is larger than the cloud optical depth feedback decrease from low clouds across CMIP models (Fig. 4b, +0.02 Wm−2K−1 per K). Retuning the CMIP models to match our observational constraint would result in a total change over the extratropics of 0.13 Wm−2K−1 (Fig. 4c, −0.023 Wm−2K−1 per K), further exacerbating the difference between CMIP6 and CMIP5 models However, re-tuning the LPR of individual models could result in larger changes because their T50/50 biases can be larger, and the outcome of a re-tuning is different depending on the model. It is important to note that in GISS-ModelE3, the mean global net feedback of the two coolest T50/50 configurations is half that of the two warmest configurations, for a T50/50 difference of 6 ˚C, which corresponds to the magnitude of a typical bias in CMIP6 models (Supplementary Table 1). Consequently, one could expect a similar impact of cloud phase changes on cloud feedback in CMIP6 models, should their T50/50 be retuned.
Effect of constraining T50/50 on ECS from CMIP6 models and GISS-ModelE3
Although the effect of constraining T50/50 on cloud feedback and ECS is surely model dependent, we aim to provide an example of possible outcome in terms of ECS uncertainty, should the T50/50 from models be modified to match the observational constraint, all else being equal. Given the strong relationship between T50/50, the extratropical SW cloud feedback (e.g., Fig. 4), the global SW cloud feedback and ECS shown in this study (e.g., Supplementary Fig. 10), we linearly regress lidar T50/50 with CMIP6 ECS, yielding a linear correlation factor (r) of 0.51. We find a slope of 0.07 ˚C of ECS per ˚C of T50/50. We then use this slope to compute the effect of correcting T50/50 biases on ECS in the 10 CMIP6 models of the study, by multiplying this slope by the corrected bias (Supplementary Table 5; model minus the closest value of the observational range) and adding it to the original ECS; we also include GISS-ModelE3 Phys in the computation, which is the configuration that best matches the observed cloud phase partitioning50). This method can be described as a direct constraint approach and has been used in previously53,56. Doing so slightly increases the mean ECS from 4.1 ˚C to 4.4 ˚C but more importantly, it also reduces the multimodel ECS standard deviation (SD) by 15%, from 1.19 ˚C to 1.01 ˚C, confirming that better constraining the cloud phase representation in CMIP6 models will result in reduced ECS inter-model spread (Fig. 7, top row). To roughly account for uncertainty in the relationship between lidar T50/50 and CMIP6 ECS, we reproduce this computation using a slope that is twice and half of 0.07 ˚C/˚C, which results in a reduction of the ECS SD by 10% and 12%, respectively, instead of 15%. An alternative method often used in the literature to constrain models, referred to as an “emergent constraint53,57,58”, consists in using the observational range of a quantity that is well correlated with ECS – for physically understood reasons – to predict ECS. The uncertainty is calculated as a function of the observational range and a 10–90% confidence interval of the slope of the ECS-T50/50 line. With this method, we find an ECS ranging from 4.02 ˚C to 4.99 ˚C with a mean of 4.4 ˚C, effectively reducing the uncertainty by 57% (Fig. 7, second row).
Applying the same methods to GISS-ModelE3, we find consistent results. By correcting T50/50 of GISS-ModelE3 configurations that are outside of the observational range with the slope of the linear regression between ECS and T50/50 (r = 0.87, p < 0.05; Supplementary Table 6), we obtain a larger ECS (3.83 ˚C compared to 3.68 ˚C) and a 33% smaller uncertainty (Fig. 7, third row). However, because the spread of T50/50 for the GISS-ModelE3 configurations is about the same as the observational range and its values do not encompass the observational range, using the 10–90% confidence interval of the slope of the ECS-T50/50 line would result in a similar or even greater uncertainty. Instead, we exclude the GISS-ModelE3 configurations that are outside of the observed T50/50 range, in which case, we obtain a mean ECS of 3.97 ˚C, ranging from 3.77 ˚C to 4.17 ˚C, which corresponds to a reduction of the ECS spread by 46% (Fig. 7, fourth row).
We note that the GISS-ModelE3 ECS values were computed through the regression method of Gregory et al.73, using 20-year runs with a slab-ocean model in which carbon dioxide was quadrupled in the perturbed runs.
Data availability
The CALIPSO-GOCCP observations (Cesana et al.31) can be downloaded from the CFMIP-Obs website (http://climserv.ipsl.polytechnique.fr/cfmip-obs/Calipso_goccp.html). The CMIP ESM outputs were downloaded from the ESGF website (https://esgf-node.llnl.gov/). The CMIP cloud feedbacks used in Fig. 4 (Zelinka, 2021) are available at https://doi.org/10.5281/zenodo.5206851. Climate model data to reproduce Figs. 1a and 2, as well as some data that is not publicly available, such as some observational datasets used in Fig. 1b, some climate model outputs (CNRM-CM6 and IPSL-CM6A-LR), which were specifically processed for this study to produce Fig. 5, as well as the GISS-ModelE3 data used in Figs. 4d and 5, can be downloaded here: https://zenodo.org/records/10767855.
Code availability
The codes used to produce the figures can be made available by contacting the corresponding author.
References
Mülmenstädt, J. et al. An underestimated negative cloud feedback from cloud lifetime changes. Nat. Clim. Chang. 11, 508–513 (2021).
Cesana, G. & Storelvmo, T. Improving climate projections by understanding how cloud phase affects radiation. J. Geophys. Res. 122, 4594–4599 (2017).
Mitchell, J. F. B., Senior, C. A. & Ingram, W. J. C02 and climate: a missing feedback? Nature 341, 132–134 (1989).
Storelvmo, T., Tan, I. & Korolev, A.V. Cloud phase changes induced by CO2 warming—a powerful yet poorly constrained cloud-climate feedback. Curr. Clim. Change Rep. 1, 288–296 (2015).
Tsushima, Y. et al. Importance of the mixed-phase cloud distribution in the control climate for assessing the response of clouds to carbon dioxide increase: A multi-model study. Clim. Dyn. 27, 113–126 (2006).
Ceppi, P., Hartmann, D. L. & Webb, M. J. Mechanisms of the negative shortwave cloud feedback in middle to high latitudes. J. Clim. 29, 139–157 (2016).
McCoy, D. T., Hartmann, D. L., Zelinka, M. D., Ceppi, P. & Grosvenor, D. P. Mixed-phase cloud physics and Southern Ocean cloud feedback in climate models. J. Geophys. Res. 120, 9539–9554 (2015).
Terai, C. R., Klein, S. A. & Zelinka, M. D. Constraining the low-cloud optical depth feedback at middle and high latitudes using satellite observations. J. Geophys. Res. 121, 9696–9716 (2016).
Zelinka, M. D. et al. Causes of higher climate sensitivity in CMIP6 Models. Geophys. Res. Lett. 47, 1–12 (2020).
McCoy, D. T., Field, P., Bodas-Salcedo, A., Elsaesser, G. S. & Zelinka, M. D. A regime-oriented approach to observationally constraining extratropical shortwave cloud Feedbacks. J. Clim. 33, 9967–9983 (2020).
IPCC. Climate Change 2021: The Physical Science Basis. Contribution of Working Group I to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change [Masson-Delmotte, V., P. Zhai, A. Pirani, S. L. Connors, C. Péan, S. Berger, N. Caud, Y. Chen,. Cambridge University Press 3949 (2021).
Sherwood, S. C. et al. An assessment of earth’s climate sensitivity using multiple lines of evidence. Rev. Geophys. 58, 1–92 (2020).
Bodas-Salcedo, A. et al. Strong dependence of atmospheric feedbacks on mixed-phase microphysics and aerosol-cloud interactions in HadGEM3. J. Adv. Model. Earth Syst. 11, 1735–1758 (2019).
Frey, W. R. & Kay, J. E. The influence of extratropical cloud phase and amount feedbacks on climate sensitivity. Clim. Dyn. 50, 3097–3116 (2018).
Tan, I., Storelvmo, T. & Zelinka, M. D. Observational constraints on mixed-phase clouds imply higher climate sensitivity. Science (1979) 352, 224–227 (2016).
Voldoire, A. et al. The CNRM-CM5.1 global climate model: Description and basic evaluation. Clim. Dyn. 40, 2091–2121 (2013).
Hourdin, F. et al. LMDZ5B: The atmospheric component of the IPSL climate model with revisited parameterizations for clouds and convection. Clim. Dyn. 40, 2193–2222 (2013).
Gettelman, A. & Morrison, H. Advanced two-moment bulk microphysics for global models. Part I: Off-line tests and comparison with other schemes. J. Clim. 28, 1268–1287 (2015).
Donner, L. J. et al. The dynamical core, physical parameterizations, and basic simulation characteristics of the atmospheric component AM3 of the GFDL global coupled model CM3. J. Clim. 24, 3484–3519 (2011).
Choi, Y. S., Ho, C. H., Kim, S. W. & Lindzen, R. S. Observational diagnosis of cloud phase in the winter Antarctic atmosphere for parameterizations in climate models. Adv. Atmos. Sci. 27, 1233–1245 (2010).
Cesana, G. & Chepfer, H. Evaluation of the cloud thermodynamic phase in a climate model using CALIPSO-GOCCP. J. Geophys. Res. Atmos. 118, 7922–7937 (2013).
Cesana, G., Kay, J. E., Chepfer, H., English, J. M. & de Boer, G. Ubiquitous low-level liquid-containing Arctic clouds: New observations and climate model constraints from CALIPSO-GOCCP. Geophys. Res. Lett. 39, 1–6 (2012).
Cesana, G., Waliser, D. E., Jiang, X. & Li, J. L. F. Multimodel evaluation of cloud phase transition using satellite and reanalysis data. J. Geophys. Res. 120, 7871–7892 (2015).
Komurcu, M. et al. Intercomparison of the cloud water phase among global climate models. J. Geophys. Res. Atmos. 119, 3372–3400 (2014).
Doutriaux-Boucher, M. & Quaas, J. Evaluation of cloud thermodynamic phase parametrizations in the LMDZ GCM by using POLDER satellite data. Geophys. Res. Lett. 31, 1–5 (2004).
Kay, J. E. et al. Evaluating and improving cloud phase in the Community Atmosphere Model version 5 using spaceborne lidar observations. J. Geophys. Res. Atmos. 121, 4162–4176 (2016).
Gettelman, A. et al. High climate sensitivity in the Community Earth System Model Version 2 (CESM2). Geophys. Res. Lett. 46, 8329–8337 (2019).
Kelley, M. et al. GISS-E2.1: Configurations and climatology. J. Adv. Model. Earth Syst. 12, e2019MS002025 (2020).
Madeleine, J.-B. et al. Improved representation of clouds in the atmospheric component LMDZ6A of the IPSL-CM6A Earth system model. J. Adv. Model. Earth Syst. 12, e2020MS002046 (2020).
Kuma, P., Bender, F. A.-M. & Jönsson, A. R. Climate model code genealogy and its relation to climate feedbacks and sensitivity. J. Adv. Model. Earth Syst. 15, e2022MS003588 (2023).
Cesana, G. et al. Using in situ airborne measurements to evaluate three cloud phase products derived from CALIPSO. J. Geophys. Res. 121, 5788–5808 (2016).
McCoy, D. T., Tan, I., Hartmann, D. L., Zelinka, M. D. & Storelvmo, T. On the relationships among cloud cover, mixed‐phase partitioning, and planetary albedo in GCMs. J. Adv. Model. Earth Syst. 8, 650–668 (2016).
Naud, C. M. et al. Thermodynamic phase profiles of optically thin midlatitude clouds and their relation to temperature., J. Geophys. Res., 115, 1–14 (2010).
Winker, D. M. et al. The CALIPSO mission. Bull. Am. Meteorol. Soc. 91, 1211–1230 (2010).
Cesana, G. & Waliser, D. E. Characterizing and understanding systematic biases in the vertical structure of clouds in CMIP5/CFMIP2 models. Geophys. Res. Lett. 43, 10,538–10,546 (2016).
Lacour, A. et al. Greenland clouds observed in CALIPSO-GOCCP: Comparison with ground-based summit observations. J. Clim. 30, 6065–6083 (2017).
Zelinka, M. D., Klein, S. A. & Hartmann, D. L. Computing and partitioning cloud feedbacks using cloud property histograms. Part II: Attribution to changes in cloud amount, altitude, and optical depth. J. Clim. 25, 3736–3754 (2012).
Moss, S. J. & Johnson, D. W. Aircraft measurements to validate and improve numerical model parametrisations of ice to water ratios in clouds. Atmos. Res. 34, 1–25 (1994).
Silber, I. et al. The prevalence of precipitation from polar supercooled clouds. Atmos. Chem. Phys. 21, 3949–3971 (2021).
Shupe, M. D. Clouds at arctic atmospheric observatories. Part II: Thermodynamic phase characteristics. J. Appl. Meteorol. Climatol. 50, 645–661 (2011).
Naud, C. M., Del Genio, A. D., Bauer, M. & Kovari, W. Cloud vertical distribution across warm and cold fronts in cloudsat-CALIPSO data and a general circulation model. J. Clim. 23, 3397–3415 (2010).
Hu, Y. et al. Occurrence, liquid water content, and fraction of supercooled water clouds from combined CALIOP/IIR/MODIS measurements. J. Geophys. Res. Atmos. 115, 1–13 (2010).
Bodas-Salcedo, A. et al. COSP: Satellite simulation software for model assessment. Bull. Am. Meteorol. Soc. 92, 1023–1043 (2011).
Tselioudis, G. et al. Evaluation of clouds, radiation, and precipitation in cmip6 models using global weather states derived from isccp-h cloud property data. J. Clim. 1–42 https://doi.org/10.1175/JCLI-D-21-0076.1 (2021)
Klein, S. A. et al. Are climate model simulations of clouds improving? An evaluation using the ISCCP simulator. J. Geophys. Res. Atmos. 118, 1329–1342 (2013).
Luo, S., Sun, Z., Zheng, X., Rikus, L. & Franklin, C. Evaluation of ACCESS model cloud properties over the Southern Ocean area using multiple-satellite products. Q. J. Royal Meteorol. Soc. 142, 160–171 (2016).
Kawai, H. et al. Significant improvement of cloud representation in the global climate model MRI-ESM2. Geosci. Model. Dev. 12, 2875–2897 (2019).
Zhang, Y. et al. Evaluation of clouds in Version 1 of the E3SM atmosphere model with satellite simulators. J. Adv. Model. Earth Syst. 11, 1253–1268 (2019).
Li, J. L. F. et al. An overview of CMIP5 and CMIP6 simulated cloud ice, radiation fields, surface wind stress, sea surface temperatures, and precipitation over tropical and subtropical oceans. J. Geophys. Res. Atmos. 125, 5–10 (2020).
Cesana, G. V., Ackerman, A. S., Fridlind, A. M., Silber, I. & Kelley, M. Snow reconciles observed and simulated phase partitioning and increases cloud feedback. Geophys. Res. Lett. 48, 1–11 (2021).
Michibata, T., Suzuki, K. & Takemura, T. Snow-induced buffering in aerosol-cloud interactions. Atmos. Chem. Phys. 20, 13771–13780 (2020).
Senior, C. A. & Mitchell, J. F. B. Carbon dioxide and climate. The impact of cloud parameterization. J. Clim. 6, 393–418 (1993).
Myers, T. A. et al. Observational constraints on low cloud feedback reduce uncertainty of climate sensitivity. Nat. Clim. Chang. 11, 501–507 (2021).
Stanford, M. W. et al. Earth-system-model evaluation of cloud and precipitation occurrence for supercooled and warm clouds over the Southern Ocean’s Macquarie Island. Atmos. Chem. Phys. 23, 9037–9069 (2023).
Terai, C. R. et al. Mechanisms behind the extratropical stratiform low-cloud optical depth response to temperature in ARM site observations. J. Geophys. Res. Atmos. 124, 2127–2147 (2019).
Klein, S. A., Hall, A., Norris, J. R. & Pincus, R. Low-cloud feedbacks from cloud-controlling factors: A review. Surv. Geophys. 38, 1307–1329 (2017).
Klein, S. A. & Hall, A. Emergent constraints for cloud feedbacks. Curr. Clim. Change Rep. 1, 276–287 (2015).
Cesana, G. V. & Del Genio, A. D. Observational constraint on cloud feedbacks suggests moderate climate sensitivity. Nat. Clim. Chang. 11, 213–218 (2021).
Forbes, R. M. & Ahlgrimm, M. On the representation of high-latitude boundary layer mixed-phase cloud in the ECMWF global model. Mon. Weather Rev. 142, 3425–3445 (2014).
Korolev, A. et al. Mixed-phase clouds: progress and challenges. Meteor. Monogr. 58, 5.1–5.50 (2017).
Konsta, D. et al. Low-level marine tropical clouds in six CMIP6 models are too few, too bright but also too compact and too homogeneous. Geophys. Res. Lett. 49, e2021GL097593 (2022).
Schuddeboom, A. J. & McDonald, A. J. The Southern Ocean radiative bias, cloud compensating errors, and equilibrium climate sensitivity in CMIP6 models. J. Geophys. Res. Atmos. 126, e2021JD035310 (2021).
Chepfer, H. et al. Use of CALIPSO lidar observations to evaluate the cloudiness simulated by a climate model. Geophys. Res. Lett. 35, L15704 (2008).
Webb, M., Senior, C., Bony, S. & Morcrette, J. J. Combining ERBE and ISCCP data to assess clouds in the Hadley Centre, ECMWF and LMD atmospheric climate models. Clim. Dyn. 17, 905–922 (2001).
Soden, B. J. et al. Quantifying climate feedbacks using radiative kernels. J. Clim. 21, 3504–3520 (2008).
Taylor, K. E. et al. Estimating shortwave radiative forcing and response in climate models. J. Clim. 20, 2530–2543 (2007).
Zelinka, M. D., Klein, S. A., Qin, Y. & Myers, T. A. Evaluating climate models’ cloud feedbacks against expert judgment. J. Geophys. Res. Atmos. 127, e2021JD035198 (2022).
Qin, Y., Zelinka, M. D. & Klein, S. A. On the correspondence between atmosphere-only and coupled simulations for radiative feedbacks and forcing from CO2. J. Geophys. Res. Atmos. 127, e2021JD035460 (2022).
Zelinka, M. D., Zhou, C. & Klein, S. A. Insights from a refined decomposition of cloud feedbacks. Geophys. Res. Lett. 43, 9259–9269 (2016).
Zelinka, M. D., Klein, S. A. & Hartmann, D. L. Computing and partitioning cloud feedbacks using cloud property histograms. Part I: Cloud radiative kernels. J. Clim. 25, 3715–3735 (2012).
Silber, I. et al. The Earth Model Column Collaboratory (EMC2) v1.1: An open-source ground-based lidar and radar instrument simulator and subcolumn generator for large-scale models. Geosci. Model. Dev. 15, 901–927 (2022).
DeMott, P. J. et al. Predicting global atmospheric ice nuclei distributions and their impacts on climate. Proc. Natl Acad. Sci. USA 107, 11217–11222 (2010).
Gregory, J. M. et al. A new method for diagnosing radiative forcing and climate sensitivity. Geophys. Res. Lett. 31, 2–5 (2004).
Acknowledgements
GC and AA were partly supported by a CloudSat-CALIPSO RTOP at the NASA Goddard Institute for Space Studies and by NASA Modeling, Analysis, Predictions program (80NSSC21K1134). IS and GC were supported by the U.S. Department of Energy’s (DOE) Atmospheric System Research, an Office of Science Biological and Environmental Research program, under grant DE-SC0021004. GC was also supported by NOAA’s Climate Program Office, Modeling, Analysis, Predictions and Projections (MAPP) program grant NA20OAR4310390. AA and AF were supported by the NASA Modeling, Analysis, and Prediction Program. Contributions of IS and AF were also supported by DOE grant DE-SC0018046. MDZ’s work was supported by the U.S. DOE Regional and Global Modeling Analysis program area and was performed under the auspices of the DOE by Lawrence Livermore National Laboratory under Contract DE-AC52-07NA27344. Resources supporting this work were provided by the NASA Center for Climate Simulation (NCCS) at Goddard Space Flight Center. We thank NASA Center for Climate Simulation (NCCS) at Goddard Space Flight Center for providing computing resources to run GISS ESM, NASA and CNES for giving access to CALIPSO observations, and Climserv for giving access to CALIPSO-GOCCP observations and for providing computing resources. We also acknowledge the World Climate Research Programme’s Working Group on Coupled Modeling, which is responsible for CMIP, and thank the climate modeling groups for producing and making available their model output. We also thank Maxwell Kelley, Takuro Michibata, Leo Donner, Jason Cole, Andrew Gettleman, Alejandro Bodas-Salcedo, and Jean-Baptiste Madeleine for addressing questions about cloud phase simulations in their climate models, Matt Shupe and Catherine Naud for providing some of the ground-based remote-sensing observations in Fig. 1b, Olivier Jourdan and Guillaume Mioche for providing some of the in situ observations in Fig. 1b, Takuro Michibata and Jennifer Kay for providing MIROC6 and CESM2 data in Supplementary Fig. 3, respectively, Tomoo Ogura for providing MIROC6 data for Figs. 1, 2 and 4, Arterm Feolilov for IPSL-CM6A-LR data for Fig. 5, Gavin Schmidt for providing useful feedback on the manuscript, and Gregory Elsaesser and Marcus Van Lier-Walqui for providing the tuning configurations for GISS-ModelE3 model. Finally, special thanks are due to Jonathan Hickman who helped us reshape the abstract and cover letter. Correspondence and requests for materials should be addressed to GC.
Author information
Authors and Affiliations
Contributions
G.C. designed the study and carried out the analysis with inputs from A.A., A.F. and I.S. A.D. and H.C. contributed to early conceptual ideas. M.Z. provided guidance on the use of model cloud feedbacks. R.R. ran additional simulations of CNRM CMIP5 and CMIP6 models. T.K. provided the temperature isolines used in Fig. 3. G.C. wrote the manuscript with contributions from all coauthors.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Communications Earth & Environment thanks the anonymous reviewers for their contribution to the peer review of this work. Primary Handling Editors: Kerstin Schepanski, Joe Aslin and Clare Davis. A peer review file is available.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Cesana, G.V., Ackerman, A.S., Fridlind, A.M. et al. Observational constraint on a feedback from supercooled clouds reduces projected warming uncertainty. Commun Earth Environ 5, 181 (2024). https://doi.org/10.1038/s43247-024-01339-1
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s43247-024-01339-1
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.