Abstract
Analyzing seismic data in a timely manner is essential for potential eruption forecasting and early warning in volcanology. Here, we demonstrate that unsupervised machine learning methods can automatically uncover hidden details from the continuous seismic signals recorded during Iceland’s 2021 Geldingadalir eruption. By pinpointing the eruption’s primary phases, including periods of unrest, ongoing lava extrusion, and varying lava fountaining intensities, we can effectively chart its temporal progress. We detect a volcanic tremor sequence three days before the eruption, which may signify impending eruptive activities. Moreover, the discerned seismicity patterns and their temporal changes offer insights into the shift from vigorous outflows to lava fountaining. Based on the extracted patterns of seismicity and their temporal variations we propose an explanation for this transition. We hypothesize that the emergence of episodic tremors in the seismic data in early May could be related to an increase in the discharge rate in late April.
Similar content being viewed by others
Introduction
Forecasting eruptions, a central aim in many volcanological studies, is complex due to the diverse and complex nature of pre-eruptive behaviors1,2,3,4. Seismic signals stand as a pivotal source of data for assessing eruptive activities, examining pre-eruptive stages, and exploring eruption precursors5. Several research efforts have analyzed seismic precursors such as seismic swarms, repeating earthquakes, and volcanic tremors3,4,6,7,8,9,10,11. Volcanic tremors, continuous seismic signals often accompanying eruptions12,13, are seen as potential geophysical markers to aid eruption prediction2,14.
Ardid et al.4 articulate that eruption precursors should meet three benchmarks: recurrency (a common pattern occurring before multiple events), transferability (occurring before eruptions in different volcanoes), and differentiability (less frequent in non-eruptive unrest). Einarsson15 underscores that recent Icelandic eruptions all exhibited short-term seismic indicators such as earthquakes and/or continuous tremors. While earthquake swarms frequently herald eruptions16, they can also arise from non-eruptive activities17,18,19,20. Volcanic tremor21, an important seismic precursor5,22, might not always serve direct forecasting purposes, given it might be overshadowed by earthquake swarms’ energy23,24, and can manifest right before and during eruptions5. Just like earthquake swarms, tremors can also happen during non-eruptive intervals25. Even though neither earthquake swarms nor volcanic tremors guarantee imminent eruptions, their observation can heighten alertness. Their concurrent presence might indicate a higher likelihood of an eruption. Additionally, volcanic tremors offer valuable insights into the internal volcanic processes23. Thus, their detection and analysis are of particular value for both eruption predictions and understanding the underlying dynamics of volcanic eruptions26,27.
Following 781 years of dormancy on the Reykjanes Peninsula, Iceland, a fissure opened near Fagradalsfjall on 19 March 202128,29,30. The eruption was preceded by a sequence of seismic swarms and intrusion events on the Reykjanes Peninsula16,31,32 commencing with a notable week-long earthquake swarm in December 201929. A 5.7 magnitude earthquake on 24 February 202129,33 marked the onset of the final seismic sequence. Three weeks later, the intrusion reached the surface, and the eruption began. While intense seismic activity was observed leading up to the Geldingadalir 2021 eruption, no precursory volcanic tremor was reported for this event30.
In volcano seismology, discerning temporal changes in the volcanic activities preceding eruptions necessitates the identification of seismic signal clusters within the continuous flow of data, as well as tracking these clusters’ relative frequencies over time. The burgeoning volume of seismological data underscores the need for swift, automated algorithms to process continuous seismic data streams. With advancements in monitoring technologies and machine learning, seismologists now have the tools to detect the early stages of volcanic eruptions and chart subsequent eruption phases with enhanced speed and precision. This study exemplifies such advancements.
By employing machine learning techniques, we analyzed the continuous seismic data from the Geldingadalir 2021 eruption in the Fagradalsfjall rifting event, uncovering patterns that traditional methods missed. These patterns not only foretold the eruption but also detailed its progression. More specifically, by using a deep learning technique, i.e., deep embedded clustering (DEC)34,35,36 which identifies hidden patterns and clusters data points without requiring labeled data (unsupervised learning), we have pinpointed distinct clusters of seismic signals corresponding to various stages of the volcanic activity. This approach can also discover key features from seismic signals, potentially detecting subtle precursors like volcanic tremors leading up to the eruption.
Our findings demonstrate the effectiveness of the DEC technique in volcano seismology for unsupervised analyzing of continuous seismic data, especially in light of the limited availability of labeled volcanic data37. Prior to this, most studies on classifying volcano-related signals using neural networks used discrete seismic events extracted from continuous seismic streams based on specific start and end times in supervised38,39 or unsupervised learning40,41,42,43.
Results
Identifying seismic signature of different eruption phases
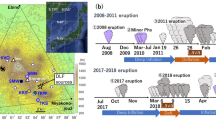
The 2021 Geldingadalir eruption features different volcanic phases such as pre-eruptive activities, continuous lava extrusion, and episodic lava fountaining. Our approach directly explores the seismic signatures related to major changes of the system. It determines dates of changes in the seismic pattern and introduces a chronology of distinguished volcanic activities, including the short-term pre-eruptive phase, lava outflow, and lava fountaining. We use seismic data from the east component of station NUPH (9 F seismic network)44 located 5.5 km southeast of the eruption site in Geldingadalir, Iceland (Fig. 1a). The signal-to-noise ratio of the tremor episodes is higher on the horizontal components compared to the vertical component45. Therefore, for our algorithm, which relies on data from a single station and a single component, we selected the east component.
a Location of the eruptive site on the Reykjanes peninsula, Iceland and the seismometer. b T-sne (t-distributed stochastic neighbor embedding is an unsupervised machine learning algorithm for visualizing high-dimensional data in a two or three-dimensional map) visualizations of seismic signal clusters in feature domain resulting from deep embedded clustering. Seismic events in each cluster correspond to a specific phase of the eruptive activity. A sample 1-hour waveform (filtered 1-4 Hz) and a photo of the eruptive site during each cluster are shown with their corresponding cluster names. Photo credits for eruptive site pictures are mentioned underneath them.
We compute the Short Time Fourier Transform (STFT) of one-hour windows of the continuous seismic data filtered from 1 to 4 Hz. The salient features of the spectrograms are automatically extracted by the convolutional layers in an autoencoder. An autoencoder is a type of artificial neural network that first transforms and compresses data into a low-dimensional representation, known as latent or feature space, and then uses these feature representations to reconstruct the original data. We apply a DEC technique in which the latent representation of the spectrograms is used for clustering. This approach ensures the extraction of the most useful features of the data for the clustering task by simultaneous optimization of feature extraction and clustering.
Using this processing approach, four clusters (EQ, CT1, ET, CT2), each corresponding with major phases of the volcanic activities (Figs. 1b and 2a), are identified. The EQ (earthquakes) cluster marks the intense seismic activity prior to the eruption. Samples in this cluster represent time windows of seismic signal when transient earthquakes are the most dominant signal (Fig. 2b, c). Most samples in this cluster start at the beginning of our data on 12 March and end before the start of the eruption (Supplementary Fig. 1a). Between the start of the eruption and 14 June we also see some windows of this cluster that contain earthquake signals (Supplementary Fig. 1b). Cluster CT1 (continuous tremors 1) initiates three days before the eruption and ends on 27 April (Fig. 2d, e). This cluster represents the continuous tremors related to processes that are active during continuous lava outflow. The seismic waveform at this time features a narrow-banded tremor with the strongest frequency at 2.5 Hz. Cluster ET (episodic tremors)—from 27 April to 13 June—contains episodic tremors related to lava fountaining (Fig. 2f, g). From 13 to 24 June, cluster CT2 (continuous tremors 2) mainly contains continuous tremors with two dominant frequencies: a narrowband frequency of 1.2 Hz, and a broader and weaker frequency between 2 to 3 Hz (Fig. 2h, i). The amplitude is higher compared to the continuous tremor in cluster CT1. Detailed information related to clusters and the volcanic processes linked with them are provided in the following.
a Four identified clusters resulted from deep embedded clustering of the continuous seismic waveform in the study time period. b, c Samples of data in the cluster EQ (earthquake). An example of a three-hour seismogram and the power spectrogram (window length of 16384 samples and overlap of 4096 samples) of data are shown in b. c presents three one-hour STFTs of seismograms as the inputs of the autoencoder (the first row) and the reconstructed outputs of the autoencoder (the second row) in this cluster. d, e Same as b, c for the cluster CT1 (continuous tremor 1). f, g, Same as b, c for the cluster ET (episodic tremor). h, i, Same as b, c for the cluster CT2 (continuous tremor 2).
Observation of precursory volcanic tremors
Volcanic tremors play an important role in volcano seismology since their pattern reflects the evolution of eruptive activities46,47,48. Although volcanic tremors are well-established short-term (days to minutes) precursors to volcanic eruptions49,50,51,52, some eruptions have occurred without such apparent precursors53,54,55,56. The 2021 Geldingadalir eruption initially has been reported to erupt without any precursory tremor30.
Using a more advanced technique, we were able to detect precursory volcanic tremors before the 2021 Geldingadalir eruption that were initially overlooked. This finding raises an important question of whether missing the detection of the precursory tremors in some eruptions was related to the data recording (insufficiently close stations to record tremors) and data processing or an underlying physical mechanism. The result of DEC shows that tremors in cluster CT1 starts three days before the eruption (Fig. 2a and Supplementary Fig. 2). An important finding here is that despite the precursory tremor signals being weak and hidden by more prominent earthquake signals, the DEC technique, known for its heightened sensitivity to subtle patterns, can effectively discern and identify them.
To investigate this finding more closely we used a signal decomposition method, i.e., harmonic-percussive separation algorithm24,57,58, and extracted the underlying volcanic tremor signal (Supplementary Note 1). Figure 3a shows seismic signals and their spectrograms between 13 and 25 March where the volcanic tremors are visible after the start of the eruption on the evening of 19 March. However, we can clearly see the tremor signal starting on 16 March in the extracted tremor plot (black rectangle in Fig. 3b). This visually confirms the observation of precursory tremors as revealed by the DEC algorithm. The spectrograms of the seismic waveform and the extracted tremors show that the precursory volcanic tremors started at noon of 16 March (Fig. 3c). Sigmundsson et al.29 show that the high rates of seismicity and deformation, which started on 24 February due to magmatic intrusion, declined from mid-March to the start of the eruption. This decrease was interpreted as resulting from tectonic stress release, reduced lateral magma migration, and the emplacement of magma in the shallow weak crust by Sigmundsson et al.29. Our observation of the precursory volcanic tremor on 16 March could also suggest that magma reached the shallow crust near the surface and indicated an upcoming eruption. Pre-eruptive tremors are mainly linked to magma movement and its interactions with gas and adjacent rocks. Considering the positioning of magma within the shallow crust from mid-March onwards29, it is possible that the detected pre-eruptive tremors are associated with this activity.
a Seismic signal and power spectrogram (window length of 32768 samples and overlap of 8192 samples) between 13 and 25 March. The blue lines marks the start of the eruption. b Extracted tremor signal from the seismic waveform using harmonic-percussive separation algorithm and the tremor spectrogram between 13 and 25 March. The black box shows the extracted tremor starting on 16 March. c, Spectrogram of the original seismic signal and the extracted tremor on 16 March. The precursory tremor starts at noon of 16 March. The black box shows the extracted tremor on 16 March.
To evaluate the ability of our algorithm to detect precursory tremors before the eruption, we conducted another test using only the available pre-eruptive data, spanning eight days from 12 to 19 March. In this test, we observed that even with a limited input size and using solely pre-eruptive data, the algorithm successfully identified a new cluster representing pre-eruptive tremors (Supplementary Fig. 3a, b). However, when we compare this result with the outcome of clustering using the entire dataset (Supplementary Fig. 3c), we see that there are additional samples in cluster CT1. A visual examination of the spectrograms revealed some misclustered samples in CT1 when we used only eight days of pre-eruptive data (Supplementary Fig. 4). These misclustered samples can be due to the small input size, which reduces the precision of the clustering task. For the pre-eruptive data, we also tested the algorithm with numbers of clusters k = 3 and k = 4. Data in cluster CT1 are almost the same for k = 2, 3, and 4, with most data occurring after 16 March. Using a number of clusters greater than 2 does not significantly change the result in cluster CT1, but it divides the EQ cluster into multiple sub-clusters, mostly based on the occurrence rate and amplitude of earthquakes in each window (Supplementary Fig. 5).
The eruption style changes
From 19 March until 27 April the eruption is characterized by low and stable effusion rate59. After 27 April the eruption style changed60 with an increased effusion rate59. Geochemical analyses of basalts and associated gas emissions indicate a rapid change in erupted composition around mid-April, shifting from lava melts initially sourced at the shallowest mantle to increasing dominance of magmas generated at greater depths60. From 2 May until 14 June, the eruptive activity is characterized by a sequence of lava fountaining45,59,61 reflected as episodic tremors on seismic data (Fig. 4b–e). Although the patterns of episodic tremors are clearly visible on raw seismic data from the beginning of the lava fountaining on 2 May, our clustering result indicates that ET tremors started earlier on 27 April at 5:00 (Fig. 2a). This is due to the higher sensitivity of our processing approach confirmed by visual examination of the spectrograms that indicates the presence of a subtle episodic pattern starting on 27 April (Supplementary Fig. 6).
a Four identified clusters resulted from deep embedded clustering of the episodic tremors. Each cluster represents episodes with different duration, amplitude, and frequency content. Four dates related to major changes in the system: 5, 11, 17 May, and 10 June are represented by blue vertical lines. b A one-hour example of seismic signal and the spectrogram (window length of 4096 samples and overlap of 1024 samples) of the cluster ET-1. c Same as b for the cluster ET-2. d Same as b for the cluster ET-3. e Same as b for the cluster ET-4.
The observation of a cluster change (CT1 to ET) and subtle episodic pattern from 27 April could indicate that the lava fountaining is triggered on 27 April by an increase in the magma flow rate. This suggests that the change in the depth of the melts generation source after mid-April and the increase in discharge rate on 27 April might have played key roles in the shift to episodic eruption behavior. On 13 June at 10:00, the ET cluster ends and the CT2 cluster starts with a dominating continuous tremor pattern. (Fig. 2a).
The variations of fountaining episodes associated with the system status
Episodic tremors of the cluster ET show distinct patterns with different duration, repose time, and amplitude45 (Fig. 4b–e). For a more detailed analysis of these episodic tremors, we performed another DEC of tremor episodes between 2 May and 14 June (lava fountaining period). This time, we used STFT of seven-minutes-long windows of the seismic signal starting from the onset time of episodes62 as the input to our model. This process resulted in four clusters (ET-1, ET-2, ET-3, ET-4) and introduced four dates related to major changes in the system: 5, 11, 17 May, and 10 June (represented by blue vertical lines in Fig. 4a). The general trend of cluster changes is in line with the detailed study of episodic tremors in Eibl et al.45 in which they linked the evolution of episodic tremor patterns to an evolving shallow magma compartment, outgassed lava accumulating in the crater edifice and a widening conduit.
Cluster ET-1 starts on 2 May. Most data in this cluster exist until 5 May at 11:56 (Fig. 4). This cluster contains episodes with a duration equal to 7 min or longer, with a dominant frequency around 1.2 Hz. The amplitude of the episodes is lower compared to other clusters. Cluster ET-2 contains episodes from 2 to 11 May (12:54) with mean duration of 4.5 min. The frequency content is similar to cluster ET-1, but the amplitude is larger. There are some episodes of this cluster between 11 and 17 May and between 10 and 13 June. Episodes in cluster ET-3 mainly start on 11 May at 15:55. They have a mean duration of 2.8 min with a fundamental frequency of around 1.4 Hz and first overtone around 2.8 Hz. The amplitude is higher compared to the other clusters. Most data in this cluster exist until 10 June, but there are some samples until 13 June as well. Cluster ET-4 contains episodes with a mean duration of 3.3 min and frequency content similar to cluster ET-3 but with lower amplitude. This cluster covers most episodes after 10 June 3:39, but it also contains some episodes from 2 May onwards, mostly after 5 May. According to the interpretations of Eibl et al.45, our clusters ET-1 and ET-2 correspond to a time period when a shallow magma compartment was modified and enlarged. Cluster ET-3 aligns with a time period when the shallow magma compartment had stabilized, featuring tremor episodes of consistent duration (see Supplementary Fig. 7a). Cluster ET-4 primarily consists of episodes in which tremor amplitude, signal-to-noise ratio, and repose time were significantly reduced following a major inner crater collapse on June 1045. The system generally exhibits a pattern of rising episode amplitude and diminishing episode duration, attributed to the erosion and widening of the vent45,61. However, this trend is frequently interrupted, potentially as a result of partial crater wall collapses45. Consequently, each cluster may include episodes occurring outside the primary time period associated with that cluster. This is particularly evident in the case of cluster ET-4, where some episodes occur almost throughout the entire lava fountaining period. Some episodes in cluster ET-4 before 10 June might be in that cluster due to strong wind noise reducing the signal-to-noise ratio on some days.
The link between the extracted features and major physical properties
Establishing a definitive link between features extracted by deep learning autoencoders and the major physical properties in seismic signals remains a largely unresolved question, suggesting a potential avenue for future exploration in this study. That said, the task of clustering episodic tremors, being simpler than clustering continuous seismic signals due to reduced input data variation and shorter durations, has offered some valuable perspectives on this matter. In the clustering of tremor episodes, the autoencoder extracts three salient features from the STFTs of episodes (Supplementary Table 1) and DEC is performed using these three features. Visual inspection of raw data for individual clusters revealed that the duration (Supplementary Fig. 7a), amplitude (Supplementary Fig. 7b), and frequency content of episodes (Supplementary Fig. 8) have the most dominant role in the clustering results. This suggests a strong connection between these three factors and the three extracted features from the autoencoder. Hence, we can infer that frequency, amplitude, and duration are the key features that characterize the overall pattern of these episodes in the seismic waveform.
Discussion
Our method provides a fast and reproducible approach for the automatic revealing of overall temporal evolution patterns of a volcanic system. Using the autoencoder to analyze raw seismic signals and automatically extract pertinent features, we can potentially uncover unexpected insights without the need for preprocessing or detailed waveform measurements. Such an approach can enhance our understanding of volcanic processes. As demonstrated in this study, our methodology successfully detected concealed pre-eruptive tremors leading up to the 2021 Geldingadalir eruption in the Fagradalsfjall rifting event and the subtle episodic tremor before lava fountaining began.
Detecting precursory volcanic tremors can be challenging due to their often weak and concealed nature, particularly when they occur within the background of seismic swarms before eruptions. The proximity of a seismic station to the eruptive site becomes crucial for recording such signals. There may be a limited number of stations in close proximity to eruptive sites, and they may not operate continuously. They might not provide data for an extended period before the eruption e.g., for dormant volcanoes or throughout the entire eruption, especially when the station is at risk of being affected by advancing lava flows. As demonstrated in our study, even with a limited dataset spanning only eight days before the eruption, we were able to identify a cluster associated with pre-eruptive tremors. However, the restricted availability of data can diminish the precision of our method and potentially result in some misclustered data. In cases of highly noisy data, the method’s performance can suffer due to the interference caused by noises. Noise, in this context, refers to random or irrelevant signals that are unrelated to volcanic activity. This interference poses challenges in accurately detecting volcano-related signals, leading to difficulties in precisely identifying signal patterns and differentiating various volcanic activity phases. Additionally, variations in noise levels over time can further complicate the task of discerning meaningful volcanic signals, impacting the method’s overall performance in accurately characterizing volcanic activity.
Our method can potentially be used in other eruptions studies and reveal the chronology of the system. This could be beneficial in revealing different phases of past activities and possibly discovering similar patterns. Volcano observatories aiming to analyze and interpret data in a timely manner may use this approach for large-scale seismic datasets in a near-real-time fashion. In a real-time observation framework, the reoccurrence of a previous cluster may inform about an upcoming similar phase only if the system has experienced it before which implies a long-term monitoring. During real-time analysis, evaluating the model’s performance on entirely new and unforeseen patterns will remain challenging since the number of clusters is determined based on the data the model has previously seen. Volcano-related signals may exhibit diverse patterns, particularly across various geographical areas. Therefore, the model should be trained using datasets specific to each volcano. For all these reasons, such methods are not yet mature enough to be integrated into an operational warning system. Applying the algorithm to well-documented eruptions is needed to further enhance our understanding of both the strengths and challenges associated with the proposed approach. When applying the algorithm across different volcanoes, it is important to take into account the frequency range associated with the tremor frequency band of each volcano, as well as the specific time resolution of interest. This consideration is needed for generating the input spectrograms of the model. Further research can explore the potential of the proposed method in real-time monitoring, examining its advantages, limitations, and challenges when applied to eruptions in different regions.
Methods
Feature extraction using autoencoder
Grouping seismic signals of volcanic activity with similar patterns could provide the potential for a deeper understanding of the volcanic processes. Clustering as a branch of unsupervised learning methods partitions unlabeled data into groups of similar objects. One of the fast and popular methods for clustering is k-means63 which clusters data based on distance metrics. However, clustering high-dimensional data is computationally expensive and usually less effective as the dimension of data increases64. Hence, dimensionality reduction and feature extraction are used before the clustering to improve the clustering results by performing the clustering in a feature space instead of the data space. The ability of deep neural networks to automatically learn cluster-friendly features has shown to be effective in improving clustering of high-dimension data65,66. Here we use an unsupervised deep learning technique named deep embedded clustering (DEC) which uses the latent representation of data extracted using an autoencoder for the clustering task34,65.
Autoencoders are neural networks that learn to compress their input data in the encoder part and decompress it in the decoder part67. The encoder learns to map the input to a latent representation through automatic feature extraction and a nonlinear transformation. The decoder reconstructs the input from the hidden representation by minimizing the reconstruction loss.
Our network consists of an autoencoder and a clustering layer, which is connected to the autoencoder’s bottleneck (Fig. 5). The encoder is composed of four two-dimensional convolutional layers followed by a fully connected neural network, which after flattening of the extracted features by convolutional neural network layers, maps them to the latent space with low dimension. The decoder has a fully connected neural network followed by four transposed convolutional layers. An Exponential Linear Unit (ELU) activation function is applied for the convolutional and fully connected layers. We use a linear activation function for the last layer in the decoder. The loss function of the autoencoder (\({{{{{{\rm{L}}}}}}}_{{{{{{\rm{R}}}}}}}\)) is the mean squared error (MSE) between the input X and the reconstructed output X’ as below:
for N samples. Details about the hyperparameters of the model are presented in Supplementary Note 2.
The encoder and decoder are composed of convolutional fully connected layers. The reconstruction loss (\({{{{{{\rm{L}}}}}}}_{{{{{{\rm{R}}}}}}}\)) and the clustering loss (\({{{{{{\rm{L}}}}}}}_{{{{{{\rm{C}}}}}}}\)), as well as t-sne plots after pre-training and after fine-tuning of the continuous seismic waveform, are given in the figure.
Deep embedded clustering
In a pre-training step the autoencoder is trained to reconstruct the output from the latent space close to the input. Then the extracted features from the bottleneck of the autoencoder are used for the clustering task using k-means algorithm. The algorithm separates the latent space into k clusters, each with a cluster centroid (\({\mu }_{j}\)). A cluster centroid is a data point that represents the center of a cluster and corresponds to the mean of all the data points within that cluster. Next, during a fine-tuning step, the model simultaneously learns feature representations and assigns clusters to the data points. First, the similarity between each embedded point \({z}_{i}\) and cluster centroids \({\mu }_{j}\) is calculated using Student’s t-distribution:
\({q}_{{ij}}\) is the probability of assigning sample i to cluster j and results in a set of soft class assignments. An auxiliary target distribution \({p}_{{ij}}\) is calculated using the membership probability \({q}_{{ij}}\) as below:
During fine-tuning clustering layer minimizes the Kullback–Leibler (KL) divergence between the soft assignments, \({q}_{{ij}}\), and the target distribution, \({p}_{{ij}}\):
Since \({q}_{{ij}}\) is the membership probability of each embedded point in each cluster, it defines the confidence of cluster assignments. The auxiliary target distribution \({p}_{{ij}}\) normalizes the loss contribution of each centroid by putting more emphasis on samples with higher confidence. So the network learns from high-confidence cluster assignments and refines the cluster centroids by minimizing the divergence between \({q}_{{ij}}\) and \({p}_{{ij}}\). During iterations in fine-tuning the cluster centroids are refined, the autoencoder weights are updated, more clustering-friendly features are learned, and the clustering results are improved. \({L}_{C}=\lambda L\) is the loss function of the clustering layer. \(\lambda\) is a hyper-parameter that weights the clustering layer. A too large \(\lambda\) will distort the latent space so the latent space will not represent the salient features of the data. A too small \(\lambda\) will eliminate the effect of clustering layer. We use 0.1 for \(\lambda\) as it is used in other studies as well34,35,65. For the optimization of the clustering layer, we use stochastic gradient descent with a momentum of 0.9 and a learning rate of 0.01. Momentum is a moving average of the gradients, and it is used to update the weight of the network. The autoencoder weights are updated every 200 iterations. Training will be stopped when the number of samples whose cluster assignments are changed reaches less than 0.01% of the total number of the input data.
Clustering continuous seismic waveform
We use continuous seismic waveform from 12 March to 24 June 2021, aiming to identify the eruptive activity phases through clustering of volcanic tremors. The seismograms were resampled to 8 Hz (to reduce the size of input data) after being demeaned and detrended. Volcanic tremors recorded on the east component of station NUPH during the 2021 Geldingadalir eruption are dominant between 1 and 4 Hz, so we use this frequency range for our study. Eibl et al.45 used this frequency range for the study of episodic tremors as well. The choice of an optimal frequency band depends on the signal of interest. For clustering of volcanic tremors, the frequency band of 1–9 Hz is commonly used as this is the usual frequency range of these signals13. When selecting different frequency bands, resampling should be adjusted accordingly.
Since volcanic tremors have a more distinct representation in the time-frequency domain compared to the time domain, we calculate the short time fourier transform (STFT) of one-hour windows of the continuous seismic signal and use the obtained spectrograms as the input for our neural network. To choose the window length, we opted to use the shortest duration that could cover the longest changing pattern such as episodic tremors here. The selected 1-h seismograms are long enough to cover most of the signal variations in the volcanic environments. Tremors with durations longer than one hour would be seen as a long-lasting signal. Other signals such as earthquakes or episodic tremors with durations of less than one hour are depicted as signals with various lengths in a 1-h window. In this step, our aim is to capture the overall pattern in the seismic data. Hence, to generalize the algorithm, we use one-hour windows of the amplitude spectrogram as the input to the autoencoder. As shown in Fig. 5, the input and output are 96 (frequency bins) by 128 (time bins), and the bottleneck has a flat dimension of 24. The architecture of our autoencoder is presented in Supplementary Table 1.
As shown in Supplementary Fig. 9a, training and validation losses exponentially decrease during autoencoder training. The ability of the autoencoder to reconstruct the input from the latent spectrogram is illustrated in Fig. 2. The structure of the spectrogram is mainly preserved after the reconstruction of the input from the encoded salient features of the latent space. This is a good indication that during the pre-training stage, the network has learned to extract a good set of features representing the essential elements of our signal of interest. The k-means clustering is then applied to the extracted features at the bottleneck of the autoencoder.
To choose the optimal number of clusters we varied the number of clusters, k, between 2 and 15 and calculated the Calinski-Harabasz (Caliński & Harabasz, 1974) index, also known as the variance ratio criterion, which is the ratio of the sum of between-clusters dispersion and of inter-cluster dispersion (Supplementary Fig. 10a). We choose the number of clusters to be 4 based on the elbow point at the Calinski-Harabasz index plot. This is the cutoff point where the index decreases much more slowly as the number of clusters increases. Figure 6a presents the initial result of k-means clustering of the latent space with the selected number of clusters 4. We visualize the data with 24 dimensions in two dimensions using t-sne method68. Next, after fine-tuning the four clusters are well separated in the t-sne plot (Fig. 6b). The good separation of clusters in the t-sne space indicates the effectiveness of the DEC algorithm in extracting the most useful features for our clustering task.
More than 99% of the samples belong to their determined cluster with high confidence: likelihood more than 0.99 (Supplementary Fig. 11). Details about samples with a likelihood below 0.99, which are presented in Supplementary Fig. 12, are discussed in Supplementary Note 3.
It is worth to mention that the clustering is done based on the salient features of the seismic signal. If there are different patterns in a time window, the k-mean distances between representative salient patterns determine the related cluster for that time window. For example, there are small earthquakes in our study time that occur in time windows that do not belong to the EQ cluster. The reason is that in those time windows in addition to the earthquake signal there is another pattern (like continuous tremor) that is more dominant compared to the earthquake signal. This means that another process represents the system state in those time windows.
Clustering episodic tremors
Episodic tremors during the 2021 Geldingadalir eruption which are the dominant pattern in the seismic signal from 2 May to 14 June, have different durations, repose times, and amplitudes and could indicate different periods of the volcanic processes. The duration of lava fountaining episodes varies between 2 and 14 min (see Supplementary Fig. 7a). For a detailed investigation on the lava fountaining episodes, we apply a DEC for the episodes. We used 7-min windows of the seismic waveform starting at the onset time of each tremor episode from Eibl et al.62. 7 min is a suitable length for our dataset considering that more than 90% of the episodes have a duration of less than 7 min.
We consider the frequency range of 1–4 Hz and calculate the STFT of the episodes for the input of the autoencoder. The autoencoder architecture is the same as we designed before. This indicates that our autoencoder does not depend on the input size and can extract features from both one-hour and 7-min spectrograms and reconstruct the input in the decoder. Here the input and output are 1536 dimensional matrices (32 frequency bins and 48 time bins) and the bottleneck has a dimension of 3 (Supplementary Table 1). The number of input spectrograms for training and validation are listed in Supplementary Table 2. For training the autoencoder, here we used the mean absolute error (MAE) loss function with a decay rate of 0.9. MAE, which is more robust to outliers and calculates the average of the absolute difference between the input and the reconstructed output.
Training and validation losses are shown in the Supplementary Fig. 9b. Some examples of the input and output of the autoencoder are shown in Supplementary Fig. 8. We apply k-means clustering on the bottleneck of the autoencoder. We choose k = 4 as the optimal number of clusters based on the Calinski-Harabasz score (Supplementary Fig. 10b). The t-sne plot before and after fine-tuning is shown in the Supplementary Fig. 13.
Data availability
Seismic data from station NUPH are available via GEOFON (Eibl et al.62, https://doi.org/10.14470/4S7576570845). The list of tremor episode start and end times is available at GFZ Data Services (Eibl et al.62, https://doi.org/10.5880/fidgeo.2022.010).
Code availability
The code related to the proposed method is freely available at https://github.com/ZahraZali/ClusTremor69.
References
Chouet, B. A. & Matoza, R. S. A multi-decadal view of seismic methods for detecting precursors of magma movement and eruption. J. Volcanol. Geotherm. Res. 252, 108–175 (2013).
Chardot, L., Jolly, A. D., Kennedy, B. M., Fournier, N. & Sherburn, S. Using volcanic tremor for eruption forecasting at White Island volcano (Whakaari), New Zealand. J. Volcanol. Geotherm. Res. 302, 11–23 (2015).
Tepp, G. & Haney, M. M. Comparison of short-term seismic precursors and explosion parameters during the 2016–2017 Bogoslof eruption. Bull Volcanol. 81, 1–15 (2019).
Ardid, A., Dempsey, D., Caudron, C. & Cronin, S. Seismic precursors to the Whakaari 2019 phreatic eruption are transferable to other eruptions and volcanoes. Nat. Commun. 13, 1–9 (2022).
Marzocchi, W., Bebbington, M. S., Marzocchi, W. & Bebbington, M. S. Probabilistic eruption forecasting at short and long time scales. Bull. Volcanol. 74, 1777–1805 (2012).
Ardid, A. et al. Using template matching to detect hidden fluid release episodes Beneath Crater Lakes in Ruapehu, Copahue, and Kawah Ijen Volcanoes. J. Geophys. Res. Solid Earth 128, e2023JB026729 (2023).
Dempsey, D. E., Cronin, S. J., Mei, S. & Kempa-Liehr, A. W. Automatic precursor recognition and real-time forecasting of sudden explosive volcanic eruptions at Whakaari, New Zealand. Nat. Commun. 11, 1–8 (2020).
Dempsey, D. E. et al. Evaluation of short-term probabilistic eruption forecasting at Whakaari, New Zealand. Bull. Volcanol. 84, 1–26 (2022).
Chastin, S. F. M. & Main, I. G. Statistical analysis of daily seismic event rate as a precursor to volcanic eruptions. Geophys. Res. Lett. 30, 1671 (2003).
Pesicek, J. D., Wellik, J. J., Prejean, S. G. & Ogburn, S. E. Prevalence of seismic rate anomalies preceding volcanic eruptions in Alaska. Front Earth Sci. (Lausanne) 6, 371306 (2018).
Roman, D. C. & Cashman, K. V. Top–down precursory volcanic seismicity: implications for ‘Stealth’ magma ascent and long-term eruption forecasting. Front Earth Sci. (Lausanne) 6, 374216 (2018).
Konstantinou, K. I. & Schlindwein, V. Nature, wavefield properties and source mechanism of volcanic tremor: a review. J. Volcanol. Geotherm. Res. 119, 161–187 (2003).
McNutt, S. R. & Nishimura, T. Volcanic tremor during eruptions: Temporal characteristics, scaling and constraints on conduit size and processes. J. Volcanol. Geotherm. Res. 178, 10–18 (2008).
Li, K. L. et al. Seismic tremor reveals slow fracture propagation prior to the 2018 eruption at Sierra Negra volcano, Galápagos. Earth Planet Sci. Lett. 586, 117533 (2022).
Einarsson, P. Short-term seismic precursors to icelandic eruptions 1973–2014. Front Earth Sci. 6, 358643 (2018).
Flóvenz, Ó. G. et al. Cyclical geothermal unrest as a precursor to Iceland’s 2021 Fagradalsfjall eruption. Nat. Geosci. 15, 397–404 (2022).
Florida, S., Benoit, J. P. & Mcnutt, S. R. Global volcanic earthquake swarm database and preliminary analysis of volcanic earthquake swarm duration. Annali di Geofisica 39, 221 (1996).
Farrell, J., Husen, S. & Smith, R. B. Earthquake swarm and b-value characterization of the Yellowstone volcano-tectonic system. J. Volcanol. Geotherm. Res. 188, 260–276 (2009).
Moran, S. C., Newhall, C. & Roman, D. C. Failed magmatic eruptions: Late-stage cessation of magma ascent. Bull Volcanol. 73, 115–122 (2011).
Shelly, D. R., Taira, T., Prejean, S. G., Hill, D. P. & Dreger, D. S. Fluid-faulting interactions: Fracture-mesh and fault-valve behavior in the February 2014 Mammoth Mountain, California, earthquake swarm. Geophys. Res. Lett. 42, 5803–5812 (2015).
McNutt, S. Volcanic Tremor. Encyclopedia of Earth System Science (1991).
Zali, Z. Volcanic tremor analysis based on advanced signal processing concepts including music Information Retrieval (MIR) Strategies https://doi.org/10.25932/PUBLISHUP-61086 (2023).
Sparks, R. S. J., Biggs, J. & Neuberg, J. W. Monitoring volcanoes. Science 335, 1310–1311 (2012).
Zali, Z., Ohrnberger, M., Scherbaum, F., Cotton, F. & Eibl, E. P. S. Volcanic tremor extraction and earthquake detection using music information retrieval algorithms. Seismol. Res. Lett. 92, 3668–3681 (2021).
Carbone, D., Zuccarello, L. & Saccorotti, G. Geophysical indications of magma uprising at Mt Etna during the December 2005 to January 2006 non-eruptive period. Geophys. Res. Lett. 35, 6305 (2008).
Chouet, B. A. Long-period volcano seismicity: its source and use in eruption forecasting. Nature 380, 309–316 (1996).
Sparks, R. S. J. Forecasting volcanic eruptions. Earth Planet Sci. Lett. 210, 1–15 (2003).
Sæmundsson, K., Sigurgeirsson, M. & Friðleifsson, G. Ó. Geology and structure of the Reykjanes volcanic system, Iceland. J. Volcanol. Geotherm. Res. 391, 106501 (2020).
Sigmundsson, F. et al. Deformation and seismicity decline before the 2021 Fagradalsfjall eruption. Nature 609, 523–528 (2022).
Barsotti, S. et al. The eruption in Fagradalsfjall (2021, Iceland): how the operational monitoring and the volcanic hazard assessment contributed to its safe access. Natural Hazards 116, 3063–3092 (2023).
Cubuk-Sabuncu, Y. et al. Temporal Seismic Velocity Changes During the 2020 Rapid Inflation at Mt. Þorbjörn-Svartsengi, Iceland, Using Seismic Ambient Noise. Geophys. Res. Lett. 48, e2020GL092265 (2021).
Geirsson, H. et al. The 2020 volcano-tectonic unrest at Reykjanes Peninsula, Iceland: stress triggering and reactivation of several volcanic systems. EGUGA https://doi.org/10.5194/EGUSPHERE-EGU21-7534 (2021).
Fischer, T. et al. Swarm seismicity illuminates stress transfer prior to the 2021 Fagradalsfjall eruption in Iceland. Earth Planet Sci. Lett. 594, 117685 (2022).
Mousavi, S. M., Zhu, W., Ellsworth, W. & Beroza, G. Unsupervised clustering of seismic signals using deep convolutional autoencoders. IEEE Geosci. Remote Sens. Lett. 16, 1693–1697 (2019).
Snover, D., Johnson, C. W., Bianco, M. J. & Gerstoft, P. Deep clustering to identify sources of urban seismic noise in long beach, California. Seismol. Res. Lett. 92, 1011–1022 (2021).
Jenkins, W. F., Gerstoft, P., Bianco, M. J. & Bromirski, P. D. Unsupervised deep clustering of seismic data: monitoring the ross Ice Shelf, Antarctica. J. Geophys. Res. Solid Earth 126, e2021JB021716 (2021).
Mousavi, S. M. & Beroza, G. C. Mach. Learn. Earthq. Seismol. 51, 105–129, https://doi.org/10.1146/annurev-earth-071822-100323 (2023).
Titos, M., Bueno, A., García, L., Benítez, C. & Segura, J. C. Classification of isolated volcano-seismic events based on inductive transfer learning. IEEE Geosci. Remote Sens. Lett. 17, 869–873 (2020).
Lara-Benítez, P., Carranza-García, M. & Riquelme, J. C. An experimental review on deep learning architectures for time series forecasting. Int. J. Neural Syst. 31 https://doi.org/10.1142/S0129065721300011, (2021).
Titos, M., Bueno, A., Garcia, L. & Benitez, C. A deep neural networks approach to automatic recognition systems for volcano-seismic events. IEEE J. Sel. Top Appl. Earth Obs. Remote Sens. 11, 1533–1544 (2018).
Anzieta, J. C., Ortiz, H. D., Arias, G. L., Ruiz, M. C. & Zuccarello, L. Finding possible precursors for the 2015 cotopaxi volcano eruption using unsupervised machine learning techniques. Int. J. Geophys. 2019, 1–8 (2019).
Canário, J. P., Mello, R., Curilem, M., Huenupan, F. & Rios, R. In-depth comparison of deep artificial neural network architectures on seismic events classification. J. Volcanol. Geotherm. Res. 401, 106881 (2020).
Duque, A. et al. Exploring the unsupervised classification of seismic events of Cotopaxi volcano. J. Volcanol. Geotherm. Res. 403, 107009 (2020).
Eibl, E. P. S., Hersir, G. P., Gudnason, E. Á. & Petursson, F. 2-year seismological experiment near Fagradalsfjall, Reykjanes peninsula in 2021/22. https://doi.org/10.14470/4S7576570845 (2022).
Eibl, E. P. S. et al. Evolving shallow conduit revealed by tremor and vent activity observations during episodic lava fountaining of the 2021 Geldingadalir eruption, Iceland. Bull Volcanol. 85, 1–20 (2023).
Alparone, S., Andronico, D., Lodato, L. & Sgroi, T. Relationship between tremor and volcanic activity during the Southeast Crater eruption on Mount Etna in early 2000. J. Geophys. Res. Solid Earth 108, 2241 (2003).
Falsaperla, S. et al. Volcanic tremor at Mt. Etna, Italy, preceding and accompanying the eruption of July - August, 2001. Pure Appl. Geophys. 162, 2111–2132 (2005).
Privitera, E., Sgroi, T. & Gresta, S. Statistical analysis of intermittent volcanic tremor associated with the September 1989 summit explosive eruptions at Mount Etna, Sicily. J. Volcanol. Geotherm. Res. 120, 235–247 (2003).
Harlow, D. H. et al. Precursory seismicity and forecasting of the June 15, 1991, eruption of Mount Pinatubo. In Fire and Mud: eruptions and lahars of Mount Pinatubo, Philippines, (eds Newhall, C. G. & Punongbayan, R. S.) 285–306 (PHIVOLCS, Univ Washington Press, Quezon, Seattle, 1996).
Hotovec, A. J., Prejean, S. G., Vidale, J. E. & Gomberg, J. Strongly gliding harmonic tremor during the 2009 eruption of Redoubt Volcano. J. Volcanol. Geotherm. Res. 259, 89–99 (2013).
Swanson, D. A. et al. Forecasts and predictions of eruptive activity at Mount St. Helens, USA: 1975–1984. J. Geodyn. 3, 397–423 (1985).
Sabit, J. P., Pigtain, R. C. & de la Cruz, E. G. The west-side story: observations of the 1991 Mount Pinatubo eruptions from the west. Fire and mud: eruptions and lahars of Mount Pinatubo, Philippines. University of Washington Press, Seattle 445–455 (1996).
Castruccio, A. et al. Eruptive parameters and dynamics of the April 2015 sub-Plinian eruptions of Calbuco volcano (southern Chile). Bull Volcanol. 78, 1–19 (2016).
Larsen, J. et al. Eruption of Alaska Volcano breaks historic pattern. EOS Trans. Am. Geophys. Union 90, 173–174 (2009).
Power, J. A. & Lalla, D. J. Seismic observations of Augustine Volcano, 1970–2007. Professional Paper 3–40 https://doi.org/10.3133/PP17691 (2010).
Reckziegel, F. et al. Forecasting volcanic ash dispersal and coeval resuspension during the April–May 2015 Calbuco eruption. J. Volcanol. Geotherm. Res. 321, 44–57 (2016).
Zali, Z., Rein, T., Krüger, F., Ohrnberger, M. & Scherbaum, F. Ocean bottom seismometer (OBS) noise reduction from horizontal and vertical components using harmonic-percussive separation algorithms. Solid Earth 14, 181–195 (2023).
Zali, Z. TremorExtractor-EqDetector. https://doi.org/10.5281/ZENODO.7339603 (2022).
Pedersen, G. B. M. et al. Volume, effusion rate, and lava transport during the 2021 Fagradalsfjall eruption: results from near real-time photogrammetric monitoring. Geophys. Res. Lett. 49, e2021GL097125 (2022).
Halldórsson, S. A. et al. Rapid shifting of a deep magmatic source at Fagradalsfjall volcano, Iceland. Nature 609, 529–534 (2022).
Lamb, O. D. et al. Acoustic observations of lava fountain activity during the 2021 Fagradalsfjall eruption, Iceland. Bull Volcanol. 84, 1–18 (2022).
Eibl, E. P. S. et al. Catalog of start and end times of lava fountaining episodes from 2 May to 14 June 2021 during the Fagradalsfjall eruption. https://dataservices.gfz-potsdam.de/panmetaworks/showshort.php?id=aed77bd7-a113-11ec-a8b4-7d2338b1cdf0https://doi.org/10.5880/fidgeo.2022.010 (2022).
MacQueen, J. Some methods for classification and analysis of multivariate observations. in Proceedings of the fifth Berkeley symposium on mathematical statistics and probability 1 281–297 (Oakland, CA, USA, 1967).
Steinbach, M., Ertöz, L. & Kumar, V. The challenges of clustering high dimensional data. N. Direct. Stat. Phys. 273–309 https://doi.org/10.1007/978-3-662-08968-2_16 (2004).
Xie, J., Girshick, R. & Farhadi, A. Unsupervised deep embedding for clustering analysis. In International conference on machine learning, pp. 478–487. PMLR, https://proceedings.mlr.press/v48/xieb16.html (2016).
Yang, B., Fu, X., Sidiropoulos, N. D. & Hong, M. Towards k-means-friendly spaces: Simultaneous deep learning and clustering. In International conference on machine learning, pp. 3861–3870. PMLR, https://proceedings.mlr.press/v70/yang17b.html (2017).
Vincent, P. et al. Stacked denoising autoencoders: Learning useful representations in a deep network with a local denoising criterion. J. Mach. Learn. Res. 11, 3371–3408 (2010).
Van der Maaten, L. & Hinton, G. Visualizing data using t-SNE. J. Mach. Learn. Res. 9, 2579–2605 (2008).
Zali, Z. ZahraZali/ClusTremor: ClusTremor https://doi.org/10.5281/ZENODO.8386966 (2023).
Acknowledgements
Zahra Zali expresses gratitude for the support provided by the German Academic Exchange Service (DAAD) through the Graduate School Scholarship Programme under Reference Number 91721165. Zahra Zali is an associated member of the DFG (Deutsche Forschungsgemeinschaft) - Research Training Group “NatRiskChange” and is thankful for their support. We extend our thanks to Frank Scherbaum for his comments on the work and in-depth discussions. We also wish to express our appreciation to the editor, Joe Aslin, the reviewer, Alberto Ardid, and the other anonymous reviewer for their insightful comments.
Funding
Open Access funding enabled and organized by Projekt DEAL. The paper is funded by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) – Project number 491466077.
Author information
Authors and Affiliations
Contributions
Z.Z. initiated the study conception and design. Z.Z. developed the algorithm and S.M.M. contributed to the algorithm’s improvement. The first manuscript draft was written by Z.Z. Z.Z., S.M.M., M.O., E.P.S.E, and F.C. contributed to the evaluation and discussion of the results and the writing of the final manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Communications Earth & Environment thanks Alberto Ardid and the other, anonymous, reviewer(s) for their contribution to the peer review of this work. A peer review file is available
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Zali, Z., Mousavi, S.M., Ohrnberger, M. et al. Tremor clustering reveals pre-eruptive signals and evolution of the 2021 Geldingadalir eruption of the Fagradalsfjall Fires, Iceland. Commun Earth Environ 5, 1 (2024). https://doi.org/10.1038/s43247-023-01166-w
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s43247-023-01166-w
This article is cited by
-
Feasibility of peak temperature targets in light of institutional constraints
Nature Climate Change (2024)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.