Abstract
Tropical cyclone risks are expected to increase with climate change and socio-economic development and are subject to substantial uncertainties. We thus assess future global tropical cyclone risk drivers and perform a systematic uncertainty and sensitivity analysis. We combine synthetic tropical cyclones downscaled from CMIP6 global climate models for several emission scenarios with economic growth factors derived from the Shared Socioeconomic Pathways and a wide range of vulnerability functions. We highlight non-trivial effects between climate change and socio-economic development that drive future tropical cyclone risk. Furthermore, we show that the choice of climate model affects the output uncertainty most among all varied model input factors. Finally, we discover a positive correlation between climate sensitivity and tropical cyclone risk increase. We assert that quantitative estimates of uncertainty and sensitivity to model parameters greatly enhance the value of climate risk assessments, enabling more robust decision-making and offering a richer context for model improvement.
Similar content being viewed by others
Introduction
Tropical cyclones (TCs) are among the most devastating natural hazards putting populations1 and assets2 at risk. TC risks (or impacts) are a function of TC hazard, exposure of people or assets to this hazard, and the respective vulnerability of the exposed people or the (built) environment3. Over the last 50 years, TCs worldwide caused, on average, 28 billion USD in economic losses every year4. In the future, TC impacts are expected to increase even further with climate change and socio-economic development1,5,6. Climate change is projected to drive an increase in TCs of the highest category, enhance precipitation rates, and amplify the destructive power of TC-induced flooding by rising sea levels7. Concurrently, socio-economic development yields an expansion of population8 and assets9 exposed to TCs. Hence, it is crucial to support at-risk communities with transparent information of future TC risk changes.
Quantifying future TC risks is particularly challenging because it requires dealing with the absence of robust verification data10,11 and large, possibly cascading uncertainties in the model input components and model structure12. To date, studies have focused on changes in the physical properties of TCs (for example, changes in intensity13 and frequency14) or future TC exposure8. No study has performed a systematic and thorough uncertainty and sensitivity analysis of future, global TC risk. We thus assess the drivers and uncertainties of direct economic damages from TCs in the future, considering wind as the driving physical hazard. Importantly, we refrain from making a priori choices regarding emission scenarios, particular global climate models (GCMs), preferable narratives developed for the Shared Socioeconomic Pathways (SSPs)15, or optimized representations of vulnerability. Instead, we include all available future TC hazard simulations and socio-economic development scenarios and represent vulnerabilities across a wide range to explore an extensive future TC risk space. Therefore, the results presented here go beyond the standard climate risk analyses, which often only provide a comparably basic uncertainty estimation but hardly ever include a thorough and systematic treatment of uncertainty and sensitivity16,17.
To study uncertainties and sensitivities in future TC risk estimates, we select from a list of scientifically justified inputs based on alternative representations of the future climate and socio-economic systems rather than defining a set of additive or multiplicative perturbation factors for each input factor whenever possible. This approach has several advantages. First, it is inherently difficult to precisely define all input uncertainties through a set of perturbation factors. Often, such information is unavailable because it is missing from future climate and socio-economic model output documentation. Second, employing a limited yet plausible range of input choices establishes a direct correlation between our output and the specific combinations of inputs employed to produce it. Lastly, we avoid assuming the likelihood of specific input combinations and instead describe the results based on the uncertainty and sensitivity observed across the explored discrete settings. Consequently, we do not investigate all uncertainties of the diverse models used to simulate such future climate and socio-economic states (e.g., the TC downscaling model or the GDP model for SSP projections). Instead, we focus on the uncertainties of the three main physical climate risk model components by sampling from a list of state-of-the-art future representations of hazard, exposure, and vulnerability.
For the hazard, we use large sets of synthetic TCs18,19,20 downscaled from nine different GCMs and three warming scenarios of the CMIP6 generation (SSP245, SSP370, SSP585), simulating TC activity of the historical period (1995–2014) and in the middle (2041–2060) and end of this century (2081–2100). This statistical-dynamical technique requires daily wind output in addition to monthly mean thermodynamic quantities and was applied for all GCMs of the newest generation, which provide this data for all ensemble members. The technique is well-established20,21 and has been shown to replicate key features of the observed historical TC climatology19. Furthermore, we use two different parametric wind models to derive 2D wind fields along each TC track22,23. Note that we do not explore uncertainties of the TC downscaling model itself; this is beyond the scope of this study and was addressed elsewhere24. However, we review the implications of this TC model choice in the discussion section in more detail. For exposure, we use economic growth factors from different SSPs15 to approximate socio-economic development and analyze exposure uncertainties. We include all five SSPs, each describing a different possible future scenario for society; ranging from a world of low economic growth, low population growth, and limited technological innovation (SSP1) to a world of high economic growth, high population growth, and rapid technological innovation (SSP5). For vulnerability, we test uncertainties by varying the vulnerability function’s slope parameter of regionally-calibrated vulnerability functions25 across a wide range. We combine these representations of hazard, exposure, and vulnerability to estimate future TC risk increases and quantify the uncertainties and sensitivities thereof using an open-source probabilistic risk model (CLIMADA)26. We repeat the risk calculations many times (>40,000), relying on a numerical Monte Carlo scheme27 to cover all possible combinations of input factor variations.
Our results highlight the full uncertainty distribution of model outputs and how these variations can be attributed to variations in input factors. This additional information is incredibly valuable to identify the most important and uncertain drivers of TC risk increase in a changing climate and evolving society. It can help model developers focus research efforts on model inputs that matter most for reducing uncertainty in the output. It may provide decision-makers with a much more representative range of plausible future outcomes and thus a more transparent and valuable information basis. Ultimately, our approach of analyzing different types of uncertainties enables better-informed adaptation decisions and mitigation strategies.
Results
Drivers of future tropical cyclone risk
We first assess the two main drivers of future TC risk increase - climate change and socio-economic development - independently and contrast them with the total risk increase later. For the independent assessment of the two TC risk drivers, we fix exposure at the reference state (year 2005, see Methods) to quantify the contribution from climate change and, analogously, evaluate socio-economically-driven risk change on historical hazard data. We express TC risk by the standard metrics of expected annual damages (EAD) and 100-year damage event (100-yr event in short). The former is the integrated value of impacts across all probabilities and is thus commonly used as a proxy for risk-based insurance premiums28. The latter is an extreme event that is expected to occur once every 100 years, on average. In other words, it is an event with a 1% chance of occurring in any given year. In this study, we focus on four distinct global regions (Fig. 1a and Methods) and evaluate the future TC risk increase relative to the respective, present-day baseline reporting results as relative changes in percent.
Relative change in tropical cyclone risk by 2050 (blue) and 2090 (orange) due to climate change (CC), socio-economic development (SOC), the product of CC and SOC calculated from the sum of their log values (sum) and both drivers interacting (total) with respect to the historical baseline. The relative change in expected annual damage (EAD) (b, c, d, e) and 100-yr event (rp100) values (f, g, h, i) are reported for the four study regions (a) North Atlantic/Eastern Pacific (AP), North Indian Ocean (IO), Southern Hemisphere (SH), and North Western Pacific (WP). Boxplots show the interquartile range (IQR) for the uncertainty over all input factors (see Methods), while the whiskers extend to 1.5 times the IQR. More extreme points (outliers) are not shown. Statistical summary metrics of all boxplots are provided in Supplementary Table 1.
We find that the median climate change-driven TC risk increase is smaller than the contribution from socio-economic development in all regions, both periods and risk metrics (Fig. 1). For example, climate change yields a median TC risk increase ranging from 0.3% (Southern Hemisphere) to 2.5% (Western Pacific) for EAD in 2050 and 0.6% (Southern Hemisphere) to 1.8% (North Indian Ocean) in 2090. On the other hand, socio-economic development causes EAD to increase by 0.8% (North Atlantic/Eastern Pacific) to 2.5% (North Indian Ocean) in 2050 and 2.0% (North Atlantic/Eastern Pacific) to 7.1% (Southern Hemisphere) in 2090 (Fig. 1b–e). We note that 100-yr event values are comparable (Fig. 1f–i), and the complete results overview can be found in Supplementary Table 1 & Supplementary Table 2. Climate change is, in most cases, the driver with the higher uncertainty, which can be deduced from the width of the interquartile range (IQR). Exceptions are results in the Southern Hemisphere for both metrics in 2090 (Fig. 1d, h) and 100-yr event values in the North Indian Ocean and Western Pacific in 2090 (Fig. 1g, i). Accordingly, extremes on both ends of the distribution are more pronounced for climate change in these cases too. Besides, climate change produces a risk decrease (−0.1% to −0.7%), whereas socio-economic development nearly always amounts to a risk increase (Supplementary Table 1 & Supplementary Table 2), implying that climate change may offset part of the socio-economically-driven TC risk increase in these cases.
Next, we evaluate the total risk increase, including both climate change and socio-economic development in the risk calculation. Most notably, the total TC risk increase (Fig. 1, total; right-most column) includes non-trivial effects between the two key drivers and it is not the mere sum of its parts nor simple, a posteriori multiplication of hazard and exposure (Fig. 1, sum; inner right column). In contrast, the total TC risk increase from the full risk calculation, including climate change applied to the hazard and socio-economic development in the exposure from the beginning, contains excess non-linearity that cannot be accounted for by the simple multiplication of hazard and exposure. Median values of total TC risk increase shown in Fig. 1 range from 2.4% (5.3%) in the North Atlantic/Eastern Pacific to 5.3% (21.7%) in the North Indian Ocean in 2050 (2090). The last value (21.7%), for example, results from the interplay of the individual contributions of climate change (1.8%) and socio-economic development (6.8%) and is notably larger than the product of the two drivers (10.1%), thus illustrating the excess non-linear effects. This non-linearity also influences the uncertainty of total TC risk increase (Fig. 1), which spans wider ranges of possible EAD and 100-yr event values than for the two single drivers and their product). It likewise affects the most extreme values. For instance, the maximum TC risk increase surpasses 400% (422% 100-yr event; 467% EAD) in the North Indian Ocean by the end of the century (Supplementary Table 1 & Supplementary Table 2). Note that we focus on total risk increases for the remainder of the study.
Sensitivity analysis of future tropical cyclone risk
The sensitivity analysis helps to determine how uncertainties in total TC risk change described in the last section can be attributed to variations in model input factors10 (Table 1). These model input factors encompass various representations of future TC hazard, exposure, and vulnerability components and uncertainties therein. Here, we present first- and total-order Sobol\({}^{{\prime} }\) sensitivity indices29,30 of our total TC risk change estimations. First-order sensitivity indices measure the effect of variations in a single input factor, and total-order sensitivity indices the combined effect of changes in multiple input factors on the model output31.
The input factor with the highest first-order sensitivity over almost all regions, periods, and metrics is the choice of GCM underlying the hazard model (GCM) (Fig. 2a). One exception is found in the Southern Hemisphere for 100-yr event values at the end of the century, where the SSP-informed GDP scaling of exposure points (SSP exposure) exhibits the largest sensitivity. This finding is also mirrored by the results in Fig. 1d, h for the Southern Hemisphere, where socio-economic development is the notably more uncertain TC risk driver than climate change. Moreover, SSP exposure has the second-highest sensitivity index in other regions. In contrast, all other input factors have little influence on the model output.
First- (a) and total-order (b) Sobol\({}^{{\prime} }\) sensitivity indices for future (2050, 2090) TC risk change expressed as %-change in expected annual damage (EAD; upper bar) and 100-yr event values (rp100; lower bar) over the four study regions (cf. Fig. 1a) North Atlantic/Eastern Pacific (AP), North Indian Ocean (IO), Southern Hemisphere (SH), and North Western Pacific (WP) and all input factors (see Methods and Table 1 therein). Results are grouped by input factors (different colors); Vulnerability function midpoint describes the impact function; Wind model; GCM, SSP hazard, Event subsampling base, Event subsampling future pertain to the hazard component; GDP model; SSP exposure, Exposure urban/rural weighting relate to the exposure.
In essence, total-order sensitivity indices broadly mirror the ranking and distribution of first-order indices (Fig. 2b). Generally, total-order sensitivity indices are higher than first-order indices, which implies interactions between input factors. However, all increases we find here are relatively small, meaning most interactions between input factors are weak. We report that the GCM model choice (GCM) still ranks as the most important factor, and the SSP-based scaling of the exposure layer (SSP exposure) is the second most important. Furthermore, we discover very small sensitivities for the wind model choice (Wind model), the two hazard sub-sampling variables (Event subsampling base/future), and the Lit (m) and Pop (n) exponent variations32 (Exposure urban/rural weighting). Note, that the latter allows emphasizing densely populated and rural areas differently (see Methods). Finally, the input factor describing the slope parameter of impact functions (Vulnerability function midpoint) has a small to moderate effect on risk output. However, we emphasize that this importance changes if we report TC risk in absolute values (Supplementary Fig. 1), in which case this input factor (Vulnerability function midpoint) controls a substantial share of the output uncertainty. Still, the GCM choice (GCM) retains a notable effect but is no longer the single key driver of the output uncertainty.
Uncertainty of future tropical cyclone risk apportioned to GCMs
We disentangle key input factors of the TC risk model to evaluate uncertainty in TC risk increase in more detail. In the last section, we showed that the GCM model choice (GCM) affects the output uncertainty of the relative change in TC risk most among all varied input factors. Here, we further investigate the role of this important modeling choice by exploiting the advantages of uncertainty analyses. We evaluate the entire distribution of output values, including all sources of uncertainties from different input factors (Table 1), split up by the nine GCMs (GCM), ordered by their transient climate response (TCR; Supplementary Table 6 and grouped by emission scenario (SSP hazard) (Fig. 3). The corresponding results for the 100-yr event (Supplementary Fig. 2) are comparable, and we thus limit the results’ description here to the EAD.
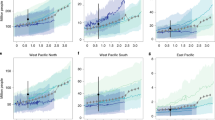
Model simulations of the expected annual damage (EAD) change by 2050 (a, c, e, g) and 2090 (b, d, f, h) attributed to the nine GCMs and three emission scenarios underlying the TC hazard sets (see Methods). GCMs are ordered by increasing transient climate response (TCR) values (Supplementary Table 6), which are shown as black stars on a secondary y-axis. Model realization of matching hazard and exposure scenarios are marked in color (SSP245 in red, SSP370 in green, SSP585 in blue) with diamond-shaped markers delineating the median of their distribution. Results are shown over the four study regions North Atlantic/Eastern Pacific (AP), North Indian Ocean (IO), Southern Hemisphere (SH), and North Western Pacific (WP) (cf. Fig. 1a).
We discover two broad GCM clusters. TC event sets downscaled from one model cluster (FGOALS, MIROC6, MPI6, MRI6, UKMO6) yield a low TC risk increase (≤10%), event sets based on the remaining models (CESM2, CNRM6, ECEARTH, and IPSL6) a medium to high-risk increase (≥10%). Particularly, simulations from the IPSL6 model stand out with the most substantial growth of TC risk (Fig. 3). Moreover, TC risk change estimates from the first GCM cluster (low-risk change) are more narrowly constrained. In contrast, models from the second cluster produce results with a much wider delta EAD range.
The selection of emission scenarios for future TC projections (SSP245, SSP370, SSP585) shapes the distribution of TC risk change estimates much less than the GCM choice (Fig. 3), which is also mirrored by the low sensitivity indices for the respective input factor (SSP hazard) described in the last section (Fig. 2). Notably, results for the GCM cluster of low TC risk increase are similar for all three hazard emission scenarios (Fig. 3). Generally, model simulations for the SSP370 hazard/SSP3 exposure combination (green colored) form the low end of the results and the SSP585 hazard/SSP5 exposure combination (blue colored) the high end (Fig. 3). Furthermore, differences between emission scenarios are more pronounced by the end of the century (Fig. 3b, d, f, h) in contrast to the middle of the century (Fig. 3a, c, e, g), which again reflects the interplay of diverging hazard and exposure projections further out into the future. Consequently, end-of-century TC risk changes are more uncertain and of greater magnitude than mid-century simulations. Lastly, the Southern Hemisphere results (Fig. 3e, f) broadly reflect outcomes described for the other regions. However, it is the region where GCM differences are smallest. There, other input factors (co-)shape the output uncertainty more strongly. Again, this finding aligns with the sensitivity indices reported in the last section.
Tropical cyclone risk change relationship to climate sensitivity
Here we link the TC risk change values resulting from TC events sets downscaled from different GCMs with the climate sensitivity of the respective model. We suggest that the intermodel differences we found and described in the last section “Uncertainty of future tropical cyclone risk apportioned to GCMs” may be related to climate sensitivity. It is known that some CMIP6-generation GCMs run hotter than others33,34. Specifically, some models of the newest generation exhibit a higher climate sensitivity than in previous generations, which lies outside the range of “likely” (or “very likely”) values as defined by authors of the Sixth Assessment Report (AR6) of the Intergovernmental Panel on Climate Change (IPCC).
We present a striking relationship between climate sensitivity and TC risk values. TCR and equilibrium climate sensitivity (ECS) values for the nine GCMs, including a screen if the models fall into the likely range of projected TCR or ECS (Supplementary Table 6), are compared to the two distinct model clusters identified in the last section. TC event sets downscaled from GCMs with climate sensitivity values in the likely range generally belong to the cluster of models we identified to produce low TC risk increases (Supplementary Table 6). The UKMO6 model constitutes the sole exception. It has a high climate sensitivity but generates low TC risk increases (Fig. 3). This qualitative assessment is supported by positive correlation coefficients calculated for TCR and TC risk values (Supplementary Table 7). The highest correlation is found between TCR values and EAD changes in the North Atlantic/Eastern Pacific in the middle of the century (0.71), the lowest correlation is between TCR and 100-yr event changes in the Southern Hemisphere at the end of the century. Besides, we calculated correlations between TCR and global TC risk changes because climate sensitivity is a global measure. The correlation coefficients are 0.39, 0.46, 0.48 and 0.54 for change in 100-yr event in 2090, 100-yr event in 2050, EAD in 2090 and EAD in 2050 respectively. Hence, on a global scale, the correlation is highest for changes in EAD in the mid-century and decreases with time and for the change in 100-yr damage values.
Discussion
Our results confirm that considering the effect of climate change alone yields an incomplete picture of future TC risk (Fig. 1). Consequently, it is important to include socio-economic development because climate impacts manifest as non-linear interactions between the two components. Hence, we find that also the uncertainty associated with future TC risk projections increases non-linearly when considering the two drivers together.
The average contribution of climate change and socio-economic development to the total future TC risk increase is of the same order of magnitude in all Northern Hemisphere regions (Fig. 1 & Supplementary Table 1 & Supplementary Table 2). But climate change is the notably more uncertain risk driver for most regions, both future periods and risk metrics, than socio-economic development (Fig. 1). We attribute the reason for this uncertainty to variations in GCMs used to downscale TCs from (Figs. 2, 3) and found the varying climate sensitivity of these GCMs as an important contributor to the dissimilar TC event sets (Section “Tropical cyclone risk change relationship to climate sensitivity”).
The case where climate change is not the more uncertain risk driver is for Southern Hemisphere end-of-century risk changes. In contrast, socio-economic development is the substantially more uncertain driver there (Fig. 1d, h & Supplementary Table 1 & Supplementary Table 2). From our study, we learn that the magnitude of socio-economically-driven risk change in the Southern Hemisphere at the end of the century is substantially larger (more than an order of magnitude) than the one of climate change. We furthermore see that the input factor for the SSP-based exposure scaling is the most important driver for the output uncertainty in this case (Fig. 2). We thus hypothesize that the SSPs describing the socio-economic growth factors by the end of the century diverge more strongly between scenarios in the Southern Hemisphere than in the other regions - explaining the uncertainty. Additionally, Southern Hemisphere SSPs may include narratives for stronger growing economies than in the North - explaining the magnitude. Furthermore, in the Southern Hemisphere, there are island states (like Indonesia) where the entire country’s GDP is exposed to TCs in contrast to large countries in the Northern Hemisphere (e.g., USA, China) whose coastal areas are exposed to TCs but areas further inland are not affected. Accordingly, the Southern Hemisphere is also the region where inter-GCM differences are lowest (Fig. 3) and the correlation to climate sensitivity is weakest (Supplementary Table 7).
Next, we discuss the findings and implications of the GCM choice (GCM) as a major determinant of output uncertainty in TC risk assessment (Fig. 2). By investigating the uncertainty space of event sets downscaled from the nine different GCMs in more detail, we found two distinct model clusters: One producing low TC risk increases, the other medium to high TC risk increases (Fig. 3). We suggest that these intermodel differences can partly be explained by climate sensitivity (Section “Tropical cyclone risk change relationship to climate sensitivity”). This correlation may not be surprising as TC potential intensity generally scales linearly with global warming35. Furthermore, TC potential intensity is a strong predictor for TC genesis potential indices36,37,38. Climate sensitivity thus helps drive TC hazard frequencies and intensities, the two critical hazard characteristics for TC risk. We are therefore not surprised to see that GCMs with frequencies and intensities below the multimodel mean broadly constitute the model cluster yielding low TC risk increases (FGOALS, MIROC6, MPI6, MRI6, UKMO6), whereas the GCMs with above-average frequencies and intensities form the second cluster (CESM2, CNRM6, ECEARTH, and IPSL6) with medium-high TC risk increases (Supplementary Table 3, Supplementary Table 4 & Supplementary Table 5). Yet, it remains to be investigated if this finding is generalizable beyond the particular statistical-dynamical TC model used in this study. We acknowledge the presence of epistemic uncertainty regarding the response of TC frequency to global warming. The TC downscaling method19 used in this study indicates increased genesis rates with global warming, especially in the northern hemisphere20, in contrast to the majority of GCMs that show decreases7. However, caution is needed when comparing the downscaling TC model to a consensus greatly influenced by GCMs with horizontal grid spacings too coarse for tropical cyclone resolution39. Notably, one NOAA Geophysical Fluid Dynamics Laboratory (GFDL) model demonstrates decreasing TC frequencies under global warming at a 50 km grid spacing, while reducing the grid spacing to 25 km alone leads to increasing genesis rates40. Similarly, the TC downscaling model by Lee et al. (2020)41 indicates varying frequency changes depending on the version of Genesis Potential Indices employed.
Besides, TC risk also depends on the track TCs take, which is not clearly related to climate sensitivity. Additionally, we did not know before our study if future TC risk change was mainly driven by climate change, socio-economic development, or the two drivers more or less equally. If the total risk were dominated by socio-economic development, we might not have found such a clear connection between TC risk increase and climate sensitivity. Indeed, our discussion of the magnitude of socio-economically-driven risk change at the end of the century Southern Hemisphere supports this statement.
In conclusion, the relationship between TC risk increase and climate sensitivity is an important discovery: we may use the climate sensitivity of GCMs as a first indicator for TC risk increase. Yet, some inter-GCM variations may arise from natural climate variability rather than only in response to increased greenhouse gas concentrations. Specifically, we used single ensemble members from each GCM and hence, any inter-GCM comparison of climate change signals will be affected by different phases of natural variability too. Moreover, it remains to be investigated if this finding is generalizable beyond the particular statistical-dynamical TC model used in this study.
These findings certainly prompt further research opportunities for TC hazard modelers. However, they are also a representation of the maturity of TC hazard modeling as a field, which is important from a risk modeling perspective. In contrast to the other key components of risk modeling - exposure and vulnerability - hazard simulations are substantially more advanced. We have many skillful models and approaches available to simulate future TCs19,41,42. But this availability is unmatched on the side of exposure and vulnerability. Hence, we should not confuse low sensitivity indices for exposure- and vulnerability-related input factors (Fig. 2) with low importance for TC risk assessment in general. The comparably low sensitivity indices for exposure and vulnerability may simply result from a limited capability to simulate socioeconomic development and changing vulnerabilities. Specifically, in this study, we neglect possible changes in vulnerability in the future because such competencies are largely nonexistent. Moreover, our choice to report the relative TC risk change and not a change in absolute terms masks the importance of the impact function-related input factor for the output uncertainty further (compare Fig. 2 & Supplementary Figure 1). For exposure, we used SSP-based GDP growth factors to approximate socio-economic development. However, the SSPs were not designed to be used in a spatially explicit fashion15, which is required for our type of risk assessment. Also, the GDP scaling ignores spatial patterns in socio-economic growth like urbanization.
These limitations consequently restrict our possibilities to inform the input factors central to the uncertainty and sensitivity analysis. In this study, we limit the input factors to all available, plausible representations of the future climate and socio-economic system. Hence, as long as such models for future exposure and vulnerability are missing, they remain blind spots in our assessment of future TC risk changes. The results from our sensitivity analysis suggest that hazard uncertainty needs to be reduced, and there is no question that more research is needed in this direction. However, our interpretation is that model maturity and complexity are not even across the three components, and therefore we recommend focusing future research efforts on better understanding and representing socio-economic development in a spatio-temporally explicit way. In parallel, improved vulnerability representations, including changing aspects of vulnerability in the future, would advance TC risk assessment further. Nonetheless, we note that TC risk estimates vary based on the chosen TC hazard model24. Similar to the epistemic uncertainty discussed for changing TC frequency in a warming climate, uncertainties exist among TC hazard models. For example, future TC risk calculations based on a fully statistical TC model42 yield comparable findings for assessing future TC risk drivers but differ in the results of the sensitivity analysis due to the differences in the underlying modeling approach and model structure43. More generally speaking, in the context of uncertainty and sensitivity analysis, the choice of model and its meta-parameters represent normative uncertainty12,44. This includes, for instance, using a risk model based on hazard, exposures, and impact functions; selecting output metrics of interest; focusing on specific large-scale regions. While most of these uncertainties are not per se quantifiable and thus not reported as results, they can be identified and discussed systematically44, particularly regarding the fitness for purpose. The here chosen model setup is designed to study uncertainties in societal TC risk at a national scale, rather than focusing on TC climatology. This justifies the choice of basin boundaries based on countries’ borders which encompass TCs originating in different basins with distinct characteristics of TC formation, intensification, and movement, and the choice of relative change in EAD and 100-y events as risk metrics. The results presented here are only meaningful within the context of this study design choice, and extrapolation to other purposes should be treated with restraint.
Ultimately, we caution against deriving strong policy statements given that the uncertainty parametrization is subject to the abovementioned limitations and biases, and only those input factors included in the study design can be analyzed for their sensitivity. However, we can still draw important, potentially policy-relevant conclusions from our analysis. We suggest using a variety of GCMs to tailor future TC risk assessments for different levels of risk aversion. For instance, to study TC risk at the very hot tail of the global model temperature change distribution, we can pick a TC event set downscaled from a GCM with high climate sensitivity. The probability of ECS exceeding 5° C is higher than 5% after all45. Considering such scenarios is important for conservative risk assessment and may be combined with a storyline approach to analyze and communicate high-impact TC in the climate change context46,47.
In conclusion, our study setup allows analyzing different types and sources of uncertainty in the same quantitative framework. Our results increase the information value of future TC risk assessment and thus provide a more transparent basis for decision-making than conventional analyses.
Methods
Study regions
We compare the increase of future TC risk over four main global regions shown in Fig. 1a and previously defined by Meiler et al. (2022)24 and also used in a study of analogous setup but different TC hazard model43. The regions broadly reflect distinct TC areas with a focus on the landmasses affected by the respective TC activity in contrast to regionalizations focused on the ocean basins of TC origin. Because we focus on the socio-economic impacts of TCs on nations as a whole, we include TCs originating in two basins for the USA, Mexico and other Central American countries with both Atlantic and Pacific coastlines. Yet, we note that TC frequencies and other shifts in TC climatology are basin-specific. Landfalling TCs originating in the North Atlantic are much more frequent and thus play a major role for the region in contrast to TCs forming in the Eastern Pacific. The diverse shifts in TC climatology in a warming climate for both basins are encompassed by the TC event set we employ. Whether changes arise from shifts in TC climatology in either basin is of secondary importance, as we quantify effects on the country’s overall GDP. While we capture these variations, we do not separate them. Hence, we combine the North Atlantic and Eastern Pacific into one region (AP) and evaluate TC risk in all of the Southern Hemisphere (SH) combined, applying the same logic as in the AP region. The North Indian Ocean (IO) and Western Pacific (WP) complete our geographical split.
Synthetic tropical cyclone tracks
Synthetic TC tracks are generated using a statistical-dynamical downscaling method developed by Emanuel et al. (200618, 200819). This method builds on three components to simulate TCs: initialization using a random seeding technique, propagation of the TCs via synthetic local winds from a beta-and-advection model, and TC intensity simulation along each track by a dynamical intensity model (CHIPS, Coupled Hurricane Intensity Prediction System)48. We note that a detailed model description and evaluation can be found in Emanuel et al. (2008)19. For this study, the TC model is driven by climate input data from nine different GCMs (Supplementary Table 8) and three emission scenarios (SSP245, SSP370, SSP585) from the CMIP6 generation. Climate models include a range of scenarios for future greenhouse gas emissions and atmospheric concentrations based on the socio-economic development described in the SSPs (Section “Socio-economic growth data”. In previous climate model generations, they were defined under the Representative Concentration Pathways (RCPs); in the newest generation, they follow the notation of the socio-economic projections. Together, the SSPs and resulting scenarios simulated in the GCMs provide a framework for exploring the potential impacts of different socio-economic and environmental futures on the global climate system. The model is run for a present climate reference state (1995–2014) and two future periods in the middle (2041–2060) and the end of this century (2081–2100). For each simulated year, 500 TCs are generated by the three steps described above. Driven by the boundary conditions of the different GCMs (e.g., sea surface temperatures and wind shear), a changing number of the initial seeds survive to become TCs. The TC frequency for each simulated year is then determined by the fraction of initial seeds and the final generated count of 500 events per year after calibrating with a constant as provided with the event set.
Socio-economic growth data
We derive economic growth factors from different SSPs to approximate socio-economic development. These factors are acquired from the SSP database, which aims to document the quantitative projections of SSPs and related Integrated Assessment scenarios (for an overview see Riahi et al., 201715). SSPs comprise five trajectories that examine how global population, economic growth, technological development, governance and social norms might change over the next century. A range of different SSP elements have been quantified (e.g., population growth, urbanization, economic development) considering the main characteristics of the SSP future development pathways. Here, we focus on economic development only, reported as GDP projections. For GDP, three alternative interpretations of the SSPs have been developed by different teams (the Organization for Economic Co-operation and Development (OECD)49, the International Institute for Applied Systems Analysis (IIASA)50 and the Potsdam Institute for Climate Impact Research (PIK)51). All resulting GDP projections were built on the same guiding assumptions for interpreting the SSPs regarding the key determinants of economic growth; however, they differ in the employed methods and outcomes. For this study, we query the SSP database for GDP growth factors for the years 2050 and 2090 for each country and all five SSPs from the three models15. Note, that the years 2050 and 2090 constitute the central time points of the respective future TC simulations for the middle and end of this century (see previous section).
Risk model CLIMADA
CLIMADA is an open-source risk model, which was created to simulate the interaction of climate and weather-related hazards, the exposure of assets or populations to this hazard, and the specific vulnerability of exposed infrastructure and people in a globally consistent fashion26,52. The model is developed and maintained as a community project, and the Python 3 source code is openly and freely available under the terms of the GNU General Public License Version 326,52. In this study, we use CLIMADA v3.253 to calculate the increase in direct economic damage from TCs in the middle and end of this century compared to a present-day baseline. We compute spatially explicit damage values on a global grid at 300 arc-seconds (~10 km) resolution.
Tropical cyclone hazard data
The TC hazard layer in CLIMADA is described by a 2D-wind field obtained from coupling TC track sets with a parametric wind model. Here, we apply two different wind models based on parameterizations following Holland (2008)22 and Emanuel and Rotunno (2011)23 to all TC track sets described above. Both parametric wind models compute the gridded 1-minute sustained winds at 10 meters above the ground as the sum of a circular wind field and the translational wind speed that arises from the TC movement. The wind models differ in their derivation of the (absolute) angular velocity from the parametric wind profile. For both wind models, the decline of the translational component from the cyclone center is incorporated by multiplying it by an attenuation factor1.
We calculate the wind fields at a resolution of 300 arc seconds (~10 km) for this study. The hazard variable used in CLIMADA is the lifetime maximum wind speed at each spatial location; values below 34 kn (17.5 ms−1) are discarded.
Asset exposure data
Exposure data for direct economic risk assessment contains information on asset value exposed to hazards. We create a dataset of spatially explicit, gridded asset exposure value using the LitPop method. LitPop distributes national estimates of total asset value to the grid level, proportional to the product of nightlight intensity (Lit) and population count (Pop)32. The present-day, reference exposure layer is computed at a resolution of 300 arc-seconds (~10 km) and the 2005 Gross Domestic Product (GDP) value (in USD). Note, that the present-day TC track sets (1995–2004) are centered around the exposure reference year 2005. Future projections of exposed asset values are constructed by scaling these reference asset values at every grid point with the growth factors derived for the two future time periods, five SSPs, and three models described above (Section “Socio-economic growth data”). The distribution of assets is thus static and is independent of future changes to the climate, the environment, and the socio-economic factors.
Impact functions
In the field of risk assessment, we use impact functions to describe vulnerability; in other words, the relationship between hazard intensity and the amount of damage it causes to assets. Impact functions are thus the critical link between hazard and exposure to calculate absolute direct damages for TC events at exposed locations. Here, we use sets of regionally calibrated impact functions25, which build on the idealized sigmoidal impact function suggested by Emanuel (2011)54. Eberenz et al. (2021)25 grouped countries of similar vulnerability into nine distinct regions and fitted impact functions to reported damage data in these regions to account for the heterogeneous picture of TC risk across the globe. In this study, we use impact functions that were calibrated on historical records25 and not synthetic TC tracks. We furthermore note that we focus on wind-driven risks in this study and neglect the explicit representation of TC risks from storm surges or TC rainfall-driven flooding. However, these sub-hazards are implicitly captured by the impact functions because they were calibrated to total damage values.
Uncertainty and sensitivity analysis
We use the uncertainty and sensitivity quantification (unsequa) module of CLIMADA12 to compute the model uncertainties and sensitivity indices reported in this study. This module seamlessly integrates the SALib - Sensitivity Analysis Library in Python package55 into the CLIMADA risk model, hence supporting all sampling and sensitivity index algorithms implemented therein. In general, the workflow of this module follows the steps of common uncertainty and sensitivity quantification schemes10,17. Here we describe the key steps in more detail.
First, we define the input factors and their variability space. Table 1 lists all input factors and the corresponding input parameter ranges, which describe the probability distributions of these random variables. Specifically, we define four input factors characterizing the hazard component of our risk model. We draw from a discrete distribution of (i) GCMs driving the TC model boundary conditions (GCM); (ii) emission scenarios (SSP hazard); (iii) wind models to calculate the 2D wind field (Wind model); and (iv) sub-sample 80% of the events in every year of the synthetic TC event set to represent natural variability (Event subsampling base, Event subsampling future). The exposure variable consists of three input factors. We sample from a discrete list of (i) GDP growth factors derived from five different SSPs (SSP exposure); (ii) three models used to translate the SSPs into economic growth factors (GDP model); and (iii) we generate exposure layers after nine different formulations of the Lit (m) and Pop (n) components to explore the uncertainty of the LitPop method. In more detail, varying the two exponents allows us to weight densely populated and rural areas differently. A higher value of n (Pop component) emphasizes highly populated areas, and a lower value the sparsely populated areas (Exposure urban/rural weighting). Note, that the total asset value remains constant. Finally, we vary the slope parameter (Vulnerability function midpoint) of the impact function, which describes the wind speed at which the function’s slope is steepest and a damage ratio of 50 % is reached. We inform the range of this parameter by the IQR of the regionally calibrated impact functions in Eberenz et al. (2021; cf. Fig. 5)25.
The next step is to draw samples of the input parameter values according to their respective uncertainty probability distribution. In this study, we use the Sobol\({}^{{\prime} }\) sampling algorithm29,30 to draw 211 samples, which translates into 40960 input factor combinations. The TC risk calculation is then executed for each combination, yielding a distribution of model outputs, which can then be analyzed and visualized. In this study, we evaluate the uncertainty in TC risk increase of the EAD and the 100-yr event. Finally, the quantification of the relative influence of the input factors on output variability is achieved by calculating sensitivity indices. We apply a variance-based method, the Sobol\({}^{{\prime} }\) quasi-Monte Carlo sequence29. Sobol\({}^{{\prime} }\) indices describe the ratio of the marginal variances to the total variance of the output metric. In this study, we evaluate first- and total-order indices. The former measures the direct contribution from each input parameter to the output variance, and the latter the overall contribution from an input parameter considering its direct effect and its interactions with all the other input parameters.
Data availability
The synthetic TC data are the property of WindRiskTech L.L.C., which is a company that provides hurricane risk assessments to clients worldwide. Upon request (info@windrisktech.com), the company provides datasets free of charge to scientific researchers, subject to a non-redistribution agreement. For this study, we used the Python (3.8+) version of CLIMADA release v3.2.053. Source code is openly and freely available under the terms of the GNU General Public License Version 326,52.
Code availability
Code to reproduce the results of this paper is available at a GitHub repository with the identifier https://doi.org/10.5281/zenodo.807335356.
References
Geiger, T., Frieler, K. & Bresch, D. N. A global historical data set of tropical cyclone exposure (TCE-DAT). Earth Syst. Sci. Data 10, 185–194 (2018). Publisher: Copernicus GmbH.
Berlemann, M. & Wenzel, D. Hurricanes, economic growth and transmission channels. World Develop. 105, 231–247 (2018). Publisher: Elsevier.
IPCC. Managing the Risks of Extreme Events and Disasters to Advance Climate Change Adaptation. A Special Report of Working Groups I and II of the Intergovernmental Panel on Climate Change [Field, C.B., V. Barros, T.F. Stocker, D. Qin, D.J. Dokken, K.L. Ebi, M.D (2012). Publication Title: Research Report ISSN: 0009-4978.
Tropical cyclones. World Meteorological Organization available at: https://public.wmo.int/en/our-mandate/focus-areas/natural-hazards-and-disaster-risk-reduction/tropical-cyclones. (accessed: 14th march 2023) (2021).
Mendelsohn, R., Emanuel, K., Chonabayashi, S. & Bakkensen, L. The impact of climate change on global tropical cyclone damage. Nat. Clim. Change 2, 205–209 (2012).
Gettelman, A., Bresch, D. N., Chen, C. C., Truesdale, J. E. & Bacmeister, J. T. Projections of future tropical cyclone damage with a high-resolution global climate model. Clim. Change 146, 575–585 (2018). Publisher: Springer Netherlands.
Knutson, T. et al. Tropical cyclones and climate change assessment part II: projected response to anthropogenic warming. Bullet. Am. Meteorol. Soc. 101, E303–E322 (2020). Publisher: American Meteorological Society.
Geiger, T., Gütschow, J., Bresch, D. N. & Emanuel, K. Double benefit of limiting global warming for tropical cyclone exposure. Nat. Clim. Change 2021 11, 861–866 (2021). Publisher: Nature Publishing Group.
Noy, I. The socio-economics of cyclones. Nat. Clim. Change 6, 343–345 (2016). Number: 4 Publisher: Nature Publishing Group.
Pianosi, F. et al. Sensitivity analysis of environmental models: a systematic review with practical workflow. Environ. Modell. Software 79, 214–232 (2016). Publisher: Elsevier Ltd.
Wagener, T., Reinecke, R. & Pianosi, F. On the evaluation of climate change impact models. WIREs Climate Change e772 (2022). Publisher: John Wiley & Sons, Ltd.
Kropf, C. M. et al. Uncertainty and sensitivity analysis for probabilistic weather and climate-risk modelling: an implementation in CLIMADA v.3.1.0. Geosci. Model Develop. 15, 7177–7201 (2022). Publisher: Copernicus GmbH.
Elsner, J. B., Kossin, J. P. & Jagger, T. H. The increasing intensity of the strongest tropical cyclones. Nature 455, 92–95 (2008). Number: 7209 Publisher: Nature Publishing Group.
Kang, N.-Y. & Elsner, J. B. Trade-off between intensity and frequency of global tropical cyclones. Nat. Clim. Change 5, 661–664 (2015).
Riahi, K. et al. The Shared Socioeconomic Pathways and their energy, land use, and greenhouse gas emissions implications: an overview. Global Environ. Change 42, 153–168 (2017).
Beven, K. J. et al. Epistemic uncertainties and natural hazard risk assessment - Part 2: what should constitute good practice? Nat. Hazards Earth Syst. Sci. 18, 2769–2783 (2018). Publisher: Copernicus GmbH.
Saltelli, A. et al. Why so many published sensitivity analyses are false: a systematic review of sensitivity analysis practices. Environ. Modell. Software 114, 29–39 (2019). ArXiv: 1711.11359 Publisher: Elsevier.
Emanuel, K., Ravela, S., Vivant, E. & Risi, C. A statistical deterministic approach to Hurricane risk assessment. Bull. Am. Meteorol. Soc. 87, S1–S5 (2006). Publisher: American Meteorological Society.
Emanuel, K., Sundararajan, R. & Williams, J. Hurricanes and global warming: results from downscaling IPCC AR4 simulations. Bull. Am. Meteorol. Soc. 89, 347–367 (2008). Publisher: American Meteorological Society.
Emanuel, K. Response of Global Tropical Cyclone Activity to Increasing CO2: Results from Downscaling CMIP6 Models. Journal of Climate 34, 57–70 (2021). Publisher: American Meteorological Society.
Emanuel, K. A. Downscaling CMIP5 climate models shows increased tropical cyclone activity over the 21st century. Proceedings of the National Academy of Sciences of the United States of America 110, 12219–12224 (2013).
Holland, G. A revised hurricane pressure-wind model. Monthly Weather Rev. 136, 3432–3445 (2008).
Emanuel, K. & Rotunno, R. Self-stratification of tropical cyclone outflow. Part I: implications for storm structure. J. Atmos. Sci. 68, 2236–2249 (2011). Publisher: American Meteorological Society.
Meiler, S. et al. Intercomparison of regional loss estimates from global synthetic tropical cyclone models. Nat. Commun. 13, 6156 (2022). Number: 1 Publisher: Nature Publishing Group.
Eberenz, S., Lüthi, S. & Bresch, D. N. Regional tropical cyclone impact functions for globally consistent risk assessments. Nat. Hazards Earth Syst. Sci. 21, 393–415 (2021).
Aznar-Siguan, G. & Bresch, D. N. CLIMADA v1: a global weather and climate risk assessment platform. Geosci. Model Develop. 12, 3085–3097 (2019). Publisher: Copernicus GmbH.
Lemieux, C. Monte Carlo and Quasi-Monte Carlo Sampling (Springer Science & Business Media, 2009).
Unterberger, C., Hudson, P., Botzen, W. J., Schroeer, K. & Steininger, K. W. Future public sector flood risk and risk sharing arrangements: an assessment for Austria. Ecol. Econ. 156, 153–163 (2019). Publisher: Elsevier.
Sobol’, I. M. Global sensitivity indices for nonlinear mathematical models and their Monte Carlo estimates. Math. Comput Simul. 55, 271–280 (2001).
Saltelli, A. et al. Variance based sensitivity analysis of model output. Design and estimator for the total sensitivity index. Comput. Phys. Commun. 181, 259–270 (2010).
Saltelli, A. Making best use of model evaluations to compute sensitivity indices. Comput. Phys. Commun. 145, 280–297 (2002).
Eberenz, S., Stocker, D., Röösli, T. & Bresch, D. N. Asset exposure data for global physical risk assessment. Earth Syst. Sci. Data 12, 817–833 (2020).
Hausfather, Z., Marvel, K., Schmidt, G. A., Nielsen-Gammon, J. W. & Zelinka, M. Climate simulations: recognize the ‘hot model’ problem. Nature 605, 26–29 (2022). Bandiera_abtest: a Cg_type: Comment Number: 7908 Publisher: Nature Publishing Group Subject_term: Climate change, Policy, Climate sciences.
He, H., Soden, B. & Kramer, R. J. On the Prevalence of High Climate Sensitivity Models. preprint, Climatology (Global Change) https://essopenarchive.org/doi/full/10.1002/essoar.10512532.1 (2022).
Emanuel, K. Environmental factors affecting tropical cyclone power dissipation. J. Clim. 20, 5497–5509 (2007). Publisher: American Meteorological Society Section: Journal of Climate.
Emanuel, K. A. & Nolan, D. S. Tropical cyclone activity and global climate. Preprints, 26th Conf. on Hurricanes and Tropical Meteorology, Miami, FL, Amer. Meteor. Soc., 240–241 (2004).
Emanuel, K. Tropical cyclone activity downscaled from NOAA-CIRES Reanalysis, 1908–1958. J. Adv. Model. Earth Syst. 2, 1 (2010).
Rappin, E. D., Nolan, D. S. & Emanuel, K. A. Thermodynamic control of tropical cyclogenesis in environments of radiative-convective equilibrium with shear: tropical cyclogenesis in variable climates. Quarterly J. Royal Meteorol. Soc. 136, 1954–1971 (2010).
Davis, C. A. Resolving tropical cyclone intensity in models. Geophys. Res. Lett. 45, 2082–2087 (2018). Publisher: Blackwell Publishing Ltd.
Vecchi, G. A. et al. Tropical cyclone sensitivities to CO2 doubling: roles of atmospheric resolution, synoptic variability and background climate changes. Clim. Dyn. 53, 5999–6033 (2019).
Lee, C.-Y., Camargo, S. J., Sobel, A. H. & Tippett, M. K. Statistical-dynamical downscaling projections of tropical cyclone activity in a warming climate: two diverging genesis scenarios. J. Clim. 33, 4815–4834 (2020).
Bloemendaal, N. et al. A globally consistent local-scale assessment of future tropical cyclone risk. Sci. Adv. 8, eabm8438 (2022). Publisher: American Association for the Advancement of Science.
Meiler, S., Ciullo, A., Bresch, D. N. & Kropf, C. M. Uncertainty and sensitivity analysis for probabilistic, global modelling of future tropical cyclone risk. 8 (Dublin, Ireland, 2023). http://hdl.handle.net/2262/103244.
Knüsel, B., Baumberger, C., Zumwald, M., Bresch, D. N. & Knutti, R. Argument-based assessment of predictive uncertainty of data-driven environmental models. Environ. Modell. Software 134, 104754 (2020).
Sherwood, S. C. et al. An assessment of earth’s climate sensitivity using multiple lines of evidence. Rev. Geophys. 58, e2019RG000678 (2020).
Shepherd, T. G. et al. Storylines: an alternative approach to representing uncertainty in physical aspects of climate change. Clim. Change 151, 555–571 (2018). Publisher: Climatic Change ISBN: 1058401823.
Ciullo, A., Martius, O., Strobl, E. & Bresch, D. N. A framework for building climate storylines based on downward counterfactuals: the case of the European Union Solidarity fund. Clim. Risk Manag. 33, 100349 (2021). Publisher: Elsevier.
Emanuel, K., DesAutels, C., Holloway, C. & Korty, R. Environmental control of tropical cyclone intensity. J. Atmos. Sci. 61, 843–858 (2004).
Dellink, R., Chateau, J., Lanzi, E. & Magné, B. Long-term economic growth projections in the Shared Socioeconomic Pathways. Glob. Environ. Change 42, 200–214 (2017).
Crespo Cuaresma, J. Income projections for climate change research: a framework based on human capital dynamics. Glob. Environ. Change 42, 226–236 (2017).
Leimbach, M., Kriegler, E., Roming, N. & Schwanitz, J. Future growth patterns of world regions - a GDP scenario approach. Glob. Environ. Change 42, 215–225 (2017).
Bresch, D. N. & Aznar-Siguan, G. CLIMADA v1.4.1: towards a globally consistent adaptation options appraisal tool. Geosci. Model Develop. 14, 351–363 (2021). Publisher: Copernicus GmbH.
Gabrielaznar et al. CLIMADA-project/climada_python: v3.2.0 https://zenodo.org/record/6807463 (2022).
Emanuel, K. A. Global warming effects on U.S. hurricane damage. Weather Clim. Soc. 3, 261–268 (2011).
Herman, J. & Usher, W. SALib: an open-source Python library for sensitivity analysis. J. Open Source Software 2, 97 (2017).
Meiler, S. simonameiler/TC_future_mit https://zenodo.org/record/8073353 (2023).
Acknowledgements
Kerry Emanuel acknowledges support from the MIT Climate Grand Challenge on Weather and Climate Extremes. This project has received funding from the European Union’s Horizon 2020 research and innovation program (grant agreement No. 820712).
Author information
Authors and Affiliations
Contributions
S.M. conceived and designed the study, analyzed the results, and wrote the manuscript. C.M.K., A.C., K.E., and D.N.B. contributed to it and supervised the analysis and interpretation of the results. K.E. provided synthetic TC tracks used as input for this study. C.M.K. wrote the unsequa module of CLIMADA, which is central to this study. All authors (S.M., A.C., C.M.K., K.E., D.N.B.) reviewed and edited the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Communications Earth & Environment thanks Ralf Toumi and the other, anonymous, reviewer(s) for their contribution to the peer review of this work. Primary Handling Editors: Min Hui Lo, Heike Langenberg. A peer review file is available
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Meiler, S., Ciullo, A., Kropf, C.M. et al. Uncertainties and sensitivities in the quantification of future tropical cyclone risk. Commun Earth Environ 4, 371 (2023). https://doi.org/10.1038/s43247-023-00998-w
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s43247-023-00998-w
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.