Abstract
Carbonatitic liquids, as a medium for transferring carbon from the slab to the mantle at subarc depths, are thought to be restricted either to the hottest conditions or to be the hydrous melting of calcium-rich lithologies (i.e., carbonated gabbro and limestone rocks) in subduction zones. In this study, high-pressure experiments on carbonated hydrous pelites demonstrate that while silicate melts are produced at 2.5–4 GPa, hydrous carbonatitic liquids clearly dominate at 5–6 GPa. The stability of Ca-rich carbonate is strongly depressed by water at pressures exceeding ~4 GPa, promoting the formation of hydrous carbonatitic liquids at temperatures as low as ~850–900 °C; these temperatures correspond to intermediate thermal regimes at depths of 150–180 km. Hence, carbonatite production beneath arcs is more pervasive than previously thought, and the carbon cycle is most likely confined to depths of less than 200 km for many subduction zones.
Similar content being viewed by others
Introduction
Subduction zones, linking the deep and shallow carbon cycles, affect the long-term habitability of the surface of Earth by regulating atmospheric CO2 concentrations1. The subducted surface carbon either penetrates deep into the Earth’s mantle, or returns to the hydrosphere and atmosphere2,3. Although the existing global flux balance creates a large scatter in the efficiency of carbon recycling, at least 18% and generally 30 to nearly 100% of carbon mobilizes out of the subducted oceanic slab2,3,4. However, the decarbonation mechanism through which carbon is likely to be transferred from the ocean slab to the mantle wedge and eventually to the volcanic arc magmas is highly debated1,2. Thermodynamic modeling has indicated that metamorphic decarbonation is negligible at subarc depths and makes minor contributions to the global carbon output flux at the convergent margins5,6,7,8. The fluid-induced dissolution of carbonate in the subducted slab has been documented on the basis that dissolved carbonate species have been observed in diamond-bearing fluid inclusions in high-pressure metamorphic rocks9; additionally, the removal of calcium carbonate along fluid conduits has been reported10. However, experimental studies, on Ca (calcium)-Mg (magnesium) carbonates have revealed that carbonate solubility in aqueous fluids decreases dramatically, by more than two orders of magnitude, as carbonate minerals transform from Ca-rich phases to Mg-rich phases11,12,13. Hence, carbonate dissolution in aqueous fluids, alone, may not supply sufficient carbon to explain the observed high CO2 outflux in magmatic arcs13,14.
Carbonatitic melts, based on experimental studies, are considered to be the primary agents to mobilize carbon out of the subducting slab at depths corresponding to Earth’s deep upper mantle and Transition Zone15,16. However, carbonatitic liquid production in the subarc regions appears to be restricted to the hottest subduction zone thermal regimes17,18 or to the hydrous melting/dissolution of carbonated gabbro14 and limestone rocks19. Therefore, in these scenarios, carbonatitic liquids, as one means to mobilize carbon out of the slab, may not be a common process at subarc depths. These schemes of carbon fractionation have largely relied on experimentally determined melting phase relationships, under water-poor or relatively dry conditions15,17,18,20,21,22,23,24. This scenario assumes that the carbonated sediments and basalts have already undergone strong dehydration during the forearc subduction stage, becoming fluid-undersaturated before reaching the subarc depths. However, subducted sediments and basalts are likely infiltrated by aqueous fluids sourced from the dehydration of serpentinites25. High CaO contents impose a strong melting-point depression on calcite in the presence of water26, consistent with the observation that the hydrous melting of Ca-rich carbonated lithologies (i.e., carbonated gabbro14 and limestone rocks19 with CaO >20 wt%) drives the formation of hydrous carbonatitic liquids towards low temperatures of 870–900 °C. However, whether other carbonated lithologies without CaO contents as high as gabbro or limestone rocks can release carbonatitic liquids in the subarc regions is unclear. Although sedimentary pelite is a primary host of subducted carbon3, the fluid-present melting behavior of carbonated pelite at subarc depths remains largely unexplored.
In this study, we have performed a series of high-pressure and high-temperature experiments to determine the phase relationships of typical carbonated pelites with compositions (Supplementary Table 1) close to Global Oceanic Subducting Sediments (GLOSS)27. Fluid-present experiments are performed over a pressure range of 2.5–6 GPa, which almost covers the entire pressure regime of the slab beneath volcanic arcs, assuming external water addition from the dehydration of underlying serpentinites. The interplay of the newly determined solidus here, and the stabilities of hydrous phases in serpentinites with modeled slab geotherms indicates that the generation of carbonatitic liquids at subarc depths is far more pervasive than previously thought.
Results and discussion
Overview
A summary of experimental conditions, run products, and their phase proportions are presented in Supplementary Table 2. Phase compositions are given in Supplementary Data 1–10. The uniform compositions of minerals throughout the entire charge, the well-crystallized grains, the limited range of the squared residuals (Σr2 = 0.01–1.22; Supplementary Table 2), and the identical pressure dependence of the stability field for equilibrium carbonate species (i.e., changing from calcite, calcite + dolomite to aragonite + magnesite with increasing pressure; Fig. 1) with carbonated basalts (e.g., ref. 17) all indicate that the system closely approaches to chemical equilibrium.
Solid and dotted red lines represent the curves along which silicate melt and carbonatitic liquid are produced, respectively. Phengite-out and crystalline carbonate-out boundaries are denoted in blue curves. The dolomite = magnesite + aragonite reaction is sourced from ref. 67. The subsolidus reaction boundary of calcite to dolomite ± aragonite reaction is inferred based on the presence of calcite from runs at 4 GPa and dolomite from supersolidus runs at 5 GPa. e-cb equilibrium carbonate, phe phengite, cbm carbonatitic liquid, sm silicate melt, csm carbonated silicate melt, mt magnetite, ky kyanite, cpx clinopyroxene, grt garnet, SiO2 – quartz at 2.5 GPa and coesite at 4–6 GPa.
Mineral phase stability
Experimental phase assemblages are summarized in the P‒T diagram in Fig. 1. The subsolidus phase assemblage consists of garnet + clinopyroxene + phengite + quartz/coesite + carbonate ± kyanite for the pressure range of 2.5‒6 GPa. The subsolidus equilibrium carbonate consists of Mg-calcite over 2.5‒4 GPa, and aragonite + magnesite at a pressure of 5‒6 GPa (Fig. 1). The appearance of aragonite and magnesite at subsolidus conditions occurs at pressures just slightly above the dolomite = aragonite + magnesite reaction boundary (Fig. 1), implying that dolomite breakdown causes the formation of aragonite and magnesite17. Due to the experimental resolutions regarding pressure and temperature, subsolidus dolomite is not observed; but calcite to dolomite reaction can be inferred to occur between 4‒5 GPa based on the presence of calcite at 4 GPa and dolomite from the supersolidus runs at 5 GPa (Fig. 1). The temperature limit of the phengite stability is over 850–900 °C at 2.5–4 GPa, between 900 and 950 °C at 5 GPa, and over 850‒900 °C at 6 GPa (Fig. 1). Equilibrium carbonates persist to higher temperatures: 900–950 °C at 2.5 GPa, >1000 °C at 4 GPa, and 1000–1050 °C for the pressure range of 5–6 GPa (Fig. 1). Magnetite occurs as a trace phase over 750‒1100 °C at 2.5 GPa, and 850‒900 °C over 4‒5 GPa, indicating that a relatively high oxygen fugacity (fO2) between NiNiO and magnetite-hematite was imposed by the oxidized starting composition and assembly (see Method). Magnetite-present experiments show that garnet is either absent or present in low proportions (<8 wt%, Supplementary Table 2), because high Fe3+/∑Fe in the starting material suppresses the formation of garnet28,29.
Diverse liquids based on quench textures
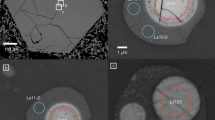
The nature of liquids at run conditions is inferred based on textural appearance (Fig. 2 and Supplementary Fig. 1) and comparisons with known experiments. The void spaces (Fig. 2a) and silicate glass spheres alone (Fig. 2b) are interpreted as quench products from subsolidus aqueous fluids30,31. At higher temperatures over the pressure range of 2.5–4 GPa, silicate glasses with tiny to large (submicron to ca. 20 µm) vesicles are observed (Fig. 2c and Supplementary Fig. 1a, b), suggesting the presence of silicate melts at these temperatures. The tiny vesicles are thought to have formed by volatile exsolution from the silicate melt upon quenching; the larger spherical vesicles indicated the equilibrium presence of CO2-rich vapor at run conditions24. A particular disequilibrium microstructure, that is, quenched carbonates, such as dendritic carbonates, irregular carbonates, CaCO3 spherulites, and CaCO3 spheres, coexisting with glass spheres and Si-Al-K-Fe rich acicular phases, is observed at 5 GPa over 900–1000 °C and at 6 GPa over 850–1150 °C (Fig. 2d, e; g–i and Supplementary Fig. 1c–f). These features are interpreted to reflect a precipitation sequence of a single, hydrous carbonatitic liquid upon thermal quenching14,16,19,32,33. As the temperatures increase to 1050 and 1100 °C over 5 and 6 GPa, respectively, relatively smooth glasses with abundant CaCO3-rich phases (Fig. 2f), which are thought to form through the extensive exsolution of carbonate upon quenching24, appear. Such textures indicate that the silicate fraction of the carbonated pelite greatly contributes to the liquid phase, and we consider that they represent CO2-rich silicate melts, which are defined as carbonated silicate melt in this study. The stability fields of various liquids are depicted in Fig. 1. In summary, for fluid-saturated, carbonated pelites, low temperatures over the entire investigated pressure range stabilize aqueous fluids, high temperatures at 2.5–4 GPa allow the production of silicate melts, intermediate temperatures at 5–6 GPa favor the formation of hydrous carbonatitic liquids, and high temperatures at 5–6 GPa facilitate the appearance of carbonated silicate melts.
DC dendritic carbonate, IC irregular carbonate, cc-sphe CaCO3 spherulite, R Si-Al-K-Fe-rich acicular phase, Dol dolomite, Grt garnet, Cpx clinopyroxene, Ky kyanite, Coe coesite. The void (a) and silicate glass sphere alone (b) are interpreted as quenched from subsolidus aqueous fluids; silicate glass with tiny vesicles (c) and glass with extensive exsolution of CaCO3-rich phase (f) are considered to be quenched silicate melt and carbonated silicate melt, respectively; a quenched mixture of quenched carbonate ± Si-Al-K-Fe-rich acicular phase ± glass sphere (d, e, g–i) that shows complex disequilibrium textures represents hydrous carbonatitic liquids under the run conditions.
Compositions of siliceous and carbonatitic liquids
Partial melting yields hydrous silicate melts at 2.5–4 GPa; whereas the liquids close to the solidus over 5–6 GPa are hydrous carbonatitic liquids, which are replaced by carbonated silicate melts at higher temperatures (Fig. 1). Silicate melts at 2.5–4 GPa are rhyodacites to dacites in their compositions while carbonated silicate melts at 5–6 GPa are trachyandesites (Supplementary Fig. 2). The silicate melt compositions of this study are generally within the same compositional range as the results from some previous experimental studies on the melting of carbonated pelites (Supplementary Fig. 2).
Hydrous carbonatitic melts cannot be quenched to glass because of their very low viscosity34, and their original compositions can be approximated by the quenched carbonate minerals14,16. In this study, quenched carbonates consist of dendritic carbonates, irregular carbonates, CaCO3-spherulites, and carbonate spheres. Dendritic carbonates and irregular carbonates from one run share identical compositions; irregular carbonates are more likely fragments detached from dendritic carbonates during polishing. Dendritic/irregular carbonates are always the only quenched carbonates in all supersolidus experiments over 5–6 GPa, except for runs at 6 GPa and 900 °C (Fig. 2h) and 6 GPa and 1050 °C (Fig. 2i), producing both dendritic carbonates and CaCO3-spherulites. Dendritic carbonates are also observed to coexist with carbonate spheres at 6 GPa and 850 °C (Fig. 2g and Supplementary Figs. 1e, 3). Dendritic carbonates and irregular carbonates are Mg-calcite in composition with XCa (molar Ca/(Ca + Mg + Fe)) ranging from 0.73 to 0.85, whereas CaCO3-spherulites are nearly pure CaCO3 end-member compositions (Supplementary Data. 2). Carbonate spheres have an intermediate XCa of 0.9 (Supplementary Fig. 3). Quenched carbonates and equilibrium crystalline carbonates are easily distinguished because (1) the former are only collected in liquid zones that concentrate on the top of capsules with distinct boundaries with residual assemblages (Fig. 2d and Supplementary Fig. 1d–f); (2) quenched carbonates and equilibrium carbonates have distinct compositions; for example, in run CY-18 (6 GPa, 850 °C), equilibrium carbonates are aragonite with XCa reaching 0.99 (Supplementary Data 3), while quenched dendritic carbonates have XCa of 0.84 (Supplementary Table 2). On average, carbonatitic liquids in this study, are calcium-rich with XCa > 0.75, with XMg < 0.25, and are comparable to carbonatitic liquids produced upon of melting of carbonated pelite and carbonated basalt with minor water; however, they are much richer in CaCO3 than those derived from the anhydrous melting of carbonated basalts and carbonated peridotites (Fig. 3).
Filled symbols represent compositions of quenched carbonates, which are close to those of hydrous carbonatitic melts. With regard to experiments CY3 (6 GPa, 900 °C) and CY14 (6 GPa, 1050 °C), two kinds of quenched carbonates with distinct compositions are produced, e.g., dendritic carbonate (Mg-calcite) and CaCO3 spherulite. Naturally-occurring carbonatites are from ref. 68; carbonatitic melts of carbonated, hydrous pelites are from ref. 24, ref. 18, and ref. 42; carbonatitic melts of hydrous, carbonated basalt are from ref. 17, ref. 69, and ref. 29; carbonatitic melts of anhydrous, carbonated basalt are from ref. 44 and ref. 23; and carbonatitic melts of hydrous carbonated peridotite are from ref. 70 and ref. 16. The carbonatitic liquids of the present study are highly calcic, having XCa = Ca/(Ca + Mg + Fe) >0.75, which is similar to previous experimental results involving the hydrous melting of carbonated basalts and carbonated pelites. The carbonatitic liquids of hydrous, carbonated basalts are more Ca-rich than those obtained from dry, carbonated basalts, confirming that the more Ca-rich the wet carbonate is, the lower the melting temperatures14,33.
Melting reactions for low-pressure silicate melts and high-pressure carbonatitic liquids
The minimum temperatures required for the studied pelites to produce silicate melts increase gradually with increasing pressure from 2.5 to ~4.5 GPa; however, they decrease by approximately 50–60 °C between 4.5 and 6 GPa as the initial liquids become essentially carbonatitic (Fig. 1). The transition from silicate melts in the low-pressure region to carbonatitic liquids in the high-pressure region, as also observed in previous hydrous melting experiments on carbonated pelites and basalts15,17,20 (Fig. 4), reflects a change in the melting sequence between silicate components and carbonates with pressure. The solidus temperatures of calcite12,35,36 show zero or a negative correlation with pressure, whereas the melting points of hydrous, CO2-free pelites37,38 and basalts39,40 increase with increasing pressure (Supplementary Fig. 4). Consequently, carbonate melting reactions will inevitably intersect the silicate solidus with increasing pressure. At pressures below the point of intersection, the melting of silicate components precedes that of carbonates, and silicate melts are produced; above the intersection, the melting of carbonates precedes that of silicate components, and carbonatitic liquids are produced. Our results, combined with previous observations on the transition from silicate melt to carbonatitic liquid (Fig. 4), suggest that the pressure of the intersection point between the silicate solidus and carbonate solidus is likely 4–5 GPa for carbonated pelites. This may explain why the first liquids are invariably siliceous by melting of carbonated pelites at pressures below 4 GPa24,28,41,42.
Solid and dotted lines represent the curves along which silicate melts and carbonatitic liquids are produced, respectively. Numbers represent the water contents of the corresponding study; for example, H03/0.12 denotes the starting bulk composition of ref. 17 contains 0.12 wt% H2O. Water-rich experiments of Ca-rich lithologies (dark blue line): carbonated gabbro, P1514; limestone, S1542, SP2019, and C2148. H2O-poor melting experiments (orange line): carbonated pelite, TS0824 and T12-Tsuno18; carbonated MORB-like basalt, H0317. Dry melting (black line): carbonated peridotite, DH671; carbonated MORB-like basalt, YB0443, D0423, K1269, and T1615. The bold sky-blue line represents the present study with 7.9 wt% H2O. The lines of slab surface temperatures for cold and hot subduction zones follow ref. 72. The minimum temperatures required to produce carbonatitic liquid at a given pressure are in the following order: black line > orange line > blue line, suggesting that water facilitates the production of carbonatitic liquids. In previous studies, the carbonatitic liquid formation was only feasible in extremely hot subduction17,18 or through the hydrous melting/or dissolution of carbonated gabbro14 and limestone rocks19 in intermediate to warm thermal regimes.
Following the methodology of ref. 43, we obtained the melting reactions based on the products and reactants of the lowest-temperature supersolidus and highest-temperature subsolidus assemblages, respectively. The average melting reactions along the solidus at 2.5–4 GPa is as follows:
At 5–6 GPa, the melting produces carbonatitic liquids through the following reactions:
Note that dolomite is inferred to be present at or slightly below the solidus at 5 GPa (see Section Overview), and an ideal dolomite composition is used to calculate its reaction coefficients (reaction 2). When reactions (2) and (3) are summarized, the average melting reaction along the solidus at 5–6 GPa is as follow:
All reactions written above are peritectic in nature. For melting reactions at 2.5–4 GPa, quartz/coesite, phengite, and clinopyroxene are the main silicates that contribute to melting, whereas only a small amount of calcite is involved in the reaction. Over a pressure range of 5–6 GPa, the coefficients of carbonate increase by ~10 times relative to those over the pressure range of 2.5–4 GPa (reaction 1 vs. reaction 4). This difference possibly causes the change in liquids from siliceous to carbonatitic. Quartz or coesite, contributing to the melt generation over 2.5–4 GPa, change side, as a function of pressure along the solidus. This is understandable because the first liquid over 5–6 GPa is (hydrous) carbonatitic in composition; therefore, all that silica, in whatever concentration, from phengite and cpx, must be absorbed by a very siliceous phase, which is only coesite. Although both garnet and kyanite are silica-bearing phases, their coefficients are simply not high enough as to absorb all the silica that comes from the contribution of phengite and cpx. A notable change from 5 to 6 GPa for melting reactions is that the coefficient of aragonite increases by ~5 times (reaction 2 vs. reaction 3). The larger contribution of aragonite to the carbonatitic liquids at 6 GPa relative to that at 5 GPa suggests that aragonite (CaCO3) in the presence of fluid becomes more fusible with increasing pressure. This finding is consistent with the observation that the solidus temperature at 6 GPa is lower than that at 5 GPa.
Controls on low temperatures to form hydrous carbonatitic liquids
The most prominent feature of the present study is that carbonatitic liquids appear at temperatures of ~850–900 °C for the pressure range of ~5–6 GPa, which are at least 100–125 °C lower than those reported by previous melting experiments on CO2-bearing basalts and pelites under dry or water-poor conditions (Fig. 4). These low temperatures for carbonatitic liquid production at subarc depths have been reported by the hydrous melting of Ca-rich lithologies (i.e., carbonated gabbro14 and limestone rocks19; see Fig. 4); however, to the best of our knowledge, the present study, for the first time, observed that the same is true for hydrous, carbonated pelites without extremely high CaO contents. Pure carbonate and complex carbonated silicate systems share very similar solidus phase relationships, temperatures, and melt compositions17,23,44; therefore, the decreased melting points of carbonates are likely responsible for the low solidus temperature observed in this study. The compositions of carbonatitic liquids in this study are highly calcic (XCa > 75, see Fig. 3), rendering the hydrous melting of CaCO3 as a plausible analog to that of hydrous carbonated pelites.
Water causes a strong depression of the solidus for CaCO3; the temperature difference between hydrous12,26,36,45,46,47 and dry35 melting below 6 GPa, to be approximately 500–1000 °C (Supplementary Fig. 4). In addition, for the binary CaCO3-MaCO3 system in the presence of water, the more Ca-rich the carbonate is, the lower melting temperatures it should have14,33; this is why the carbonatitic liquids of hydrous eclogite are more Ca-rich than those obtained from the dry one (Fig. 3). Comparing the results of this study with previous similar studies on hydrous, carbonated pelites confirms the importance of water and Ca-rich carbonate to drive the formation of carbonatitic liquids toward low temperatures. Our experiments have identical subsolidus carbonate assemblages (low-pressure Mg-calcite to high-pressure aragonite + magnesite) with hydrous experiments by ref. 24 and ref. 20; however, the minimum temperatures to form carbonatitic liquids differ by ~150 °C (see TS08 and GS11 in Fig. 4). This difference is partly attributable to the flux effect of water because their experiments were conducted under fluid-undersaturated conditions. In addition, the alumina-rich, carbonated pelite bulk composition (23 wt% Al2O3 on a volatile-free basis; see AM in Supplementary Table 1) they used could stabilize the high amount of phengite and clinopyroxene, which suppress the release of the fusible elements (e.g., K and Na) to carbonatitic liquids and shift the solidus to high temperatures. The hydrous melting experiments from ref. 18 (see T12 in Fig. 4) were conducted with a slight excess of water, but their carbonatite solidus at 5 GPa is still ~30–50 °C higher than that of the current study. This difference may arise from compositional variations in subsolidus carbonates, which were Mg-calcite (MgO = ~10 wt%) in their study and aragonite (nearly pure CaCO3) in our study. Mg-bearing CaCO3 is more refractory than pure CaCO3 in the presence of water, and this conclusion holds true from the perspective of both melting14,33 and dissolution13. Ca-rich carbonated lithologies tend to stabilize Ca-rich carbonates, such as aragonite, at pressures above ~4 GPa14,33; therefore, hydrous, Ca-rich bulk components favor the formation of hydrous carbonatitic liquids at low temperatures (e.g., refs. 14,19). In summary, the strong effect of water in depressing the solidus of CaCO3 combined with the stabilization of aragonite (nearly pure CaCO3, Supplementary Data 2) in the subsolidus phase assemblage for the pressure range of ~5–6 GPa, results in the formation of carbonatitic liquids at temperatures as low as ~850–900 °C.
Development of a negative Clapeyron slope for the solidus at ~5–6 GPa
Another feature of the present study is the decrease in solidus temperature as the pressure increases from ~5 to 6 GPa. In previous H2O-bearing melting experiments of impure limestone rocks, the solidus has also shown a decrease from >950–1100 °C at pressures below 3 GPa42,48 to between 850–900 °C over 4.2–6 GPa19. Most recently, such a melting curve has been observed for ophicarbonate49. The trend of decreasing solidus temperatures with increasing pressure is attributed to increasing H2O solubility in carbonatitic liquids with increasing pressure49. However, the mechanism by which increasing H2O solubility in carbonatitic liquids relates to solidus depression is unclear. Alternatively, we attempt to explain a negative slope for the carbonate solidus from the perspective of its definition. The Clapeyron slope of the solidus dT /dP = ΔV/ΔS = T ΔV /ΔH is governed by the entropy of fusion (ΔS = S liquid –S solid) and the volume of fusion (ΔV = V liquid – V solid). Since melting is usually an endothermic process (ΔH > 0), ΔS is positive. An exception is that the melting of calcite V into an aragonite-like high-pressure liquid causes a large decrease in enthalpy (i.e., ΔH < 0) due to the enhanced diffusive motion of oxygen in the former50. However, based on the summarized phase relationships of CaCO335, the carbonate near the solidus at a pressure of 5–6 GPa lies in the stability field of aragonite. Hence the sign of the solidus slope is determined by the ΔV term: a positive sign indicates that the liquid is less dense than the solid, and, a negative sign implies a density crossover between the liquid and solid.
The melting curve of dry CaCO3 has been experimentally constructed at a pressure of 3–21 GPa (e.g., refs. 35,51). Their results show that (1) the melting curve slope is positive from 3 to 7 GPa (Supplementary Fig. 4), indicating that the liquid is less dense than the solid (i.e., ΔV > 0); (2) as the pressure increases, the slope flattens and becomes negative near 8 GPa (Supplementary Fig. 4), indicating that the liquid is denser than the solid and it becomes more compressible at this pressure (i.e., ΔV < 0). Density measurements experiments on hydrous carbonatitic liquids have shown that their densities increase with decreasing temperature or increasing pressure52. In addition, the densities of hydrous carbonatitic liquids are only ~5% smaller than the dry counterparts52. The temperatures at which hydrous carbonatitic liquids appear are ~900 °C lower than that of dry CaCO3 at a pressure of 5–6 GPa (Supplementary Fig. 4). Such a large drop in temperature may largely increase the densities of hydrous carbonatitic liquids and shift the pressure at which density crossover (from ρ solid > ρ liquid to ρ solid < ρ liquid, corresponding to ΔV > 0 to ΔV < 0) occurs from 8 to <5 GPa. The negative volume of melting is likely the root cause of the negative slope of carbonatitic solidus for the pressure range ~5–6 GPa.
Pervasive formation of hydrous carbonatitic liquids by flux melting of carbonated pelite in the subarc region
The fluid-present melting of carbonated pelites in the subarc regions is achieved when external water derived from underlying serpentinized peridotites is available53,54. Antigorite and chlorite are the main hydrous phases in serpentinites, which contain up to ~13 wt% structurally bound water; these hydrous minerals are increasingly recognized as an important water source for arc-magma genesis55,56. The reported solidus of the carbonated, hydrous pelite from this study and the previously constructed dehydration histories of hydrated ultramafic rocks allow an examination of slab geothermal conditions to form hydrous carbonatitic liquids (Fig. 5). To achieve flush melting of subducted carbonated pelites, concomitant dehydration of within the underlying hydrated layer is necessary54. Considering the large temperature gradients within the subducting slab, the above scenario requires a very particular thermal structure: temperatures at the slab surface are high enough to produce hydrous carbonatitic liquids, while temperatures within the underlying serpentinized mantle can destabilize antigorite or chlorite54.
Thermal conditions of warm (dark red), intermediate (dark blue), and cold (dark purple) subduction zones at the slab top and slab Moho (7 km below the slab surface; brighter fields of the immediately aforementioned thermal profiles) are after Syracuse et al.72. The lower pressure (<4.5 GPa) red line separates aqueous fluids from hydrous silicate melts, whereas the higher pressure (>4.5 GPa) red line marks a boundary between aqueous fluids from hydrous carbonatitic liquids. Atg represents antigorite–serpentinite and Chl represents Chlorite. Phase relationships involving antigorite-serpentine are from ref. 73, and chlorite, 10 Å, and Phase A are from ref. 55. The front and back numbers are the amounts of water bound to hydrous phases for harzburgite and lherzolite, respectively39. Serpentinized peridotites below the oceanic crust will undergo strong dehydration at depths of between 140 and 180 km (depth interval between points I and II) when intermediate subduction paths intersect the antigorite—10 Å boundary, providing large amounts of water (green arrow) to trigger flux melting of overlying carbonated pelite.
Hydrous carbonatitic liquids are observed at temperatures between ~850 and 900 °C over ~5–6 GPa, corresponding to the intermediate thermal regimes of the slab surface at depths of ~150–180 km (Fig. 5); simultaneously, the temperatures at the slab Moho under intermediate thermal conditions exceed the stability limits of antigorite and chlorite, resulting in successive dehydration at depths of ~140–180 (depth interval between point I and II; see Fig. 5). Consequently, the stratified subducted slab, the thermal gradient from the slab surface to the interior, and the temperature differences between the breakdown of the hydrous phases and the defined solidus in this study, make an intermediate slab geotherms a favorable condition for scavenging CO2 from a slab by hydrous carbonatitic liquids. Our results thus suggest that carbonatitic liquid production is not necessarily limited to hot-slab environments or to the hydrous melting of Ca-rich lithologies. The transfer of carbon from the slab to the mantle by hydrous carbonatitic liquids in the subarc regions should be a common process. For many subduction zones, the pervasive production of hydrous carbonatitic liquids may restrict the subduction of carbon into the Earth beyond 200 km. These extremely mobile and reactive hydrous calcium carbonatitic liquids are expelled from the slab; they ascend into the overlying mantle wedge, where they react with the ambient peridotitic mantle to form olivine-rich domains by consuming orthopyroxene57. The occurrence of low-Ni olivine in subduction-related Ca-rich, silica-undersaturated rocks is thought to reflect the interactions between the mantle peridotite and CaCO3-rich carbonatitic liquids58.
Methods
Starting materials
This starting composition was synthesized using reagent grade oxides (SiO2, Fe2O3, and MnO), carbonates (CaCO3 and K2CO3), and hydroxides (Al(OH)3, NaOH, and Mg(OH)2). The starting material is highly oxidized because all Fe was introduced as Fe2O3. To minimize the absorbed H content in the starting mix, SiO2, Fe2O3, and MnO were heated overnight at 800 °C, CaCO3 at 200 °C, K2CO3, Al(OH)3, NaOH, and Mg(OH)2 at 120 °C. SiO2, Fe2O3, MnO, and K2CO3 were first mixed and ground in an agate mortar with acetone for chemical homogeneity. The mixture was decarbonated at 1000 °C for 10 h and then fused at 1500 °C for 30 min. The quenched glass was then ground to produce silicate powder. Subsequently, 7.89 wt% H2O, as Al(OH)3, NaOH, and Mg(OH)2, and 6.09 wt% CO2 as CaCO3 were added to the resulting glass, followed by re-grinding. The starting material was analysed by X-ray fluorescence spectrometry (XRF), from which the amount of H2O and CO2 was accurately determined based on the proportion of Al2O3, Na2O, and MgO, and the proportion of CaO, respectively. The bulk composition has an atomic H: K ratio of 22, which is much higher than that of phengite (~2), indicating that the starting bulk composition is fluid-saturated under subsolidus conditions.
High-pressure experiments
High-pressure experiments were performed using a piston-cylinder apparatus and a 2500-ton multi-anvil press, which are installed in Guangzhou Institute of Geochemistry, Chinese Academy of Sciences, over the pressure and temperature range of 2.5–6 GPa and 750–1100 °C, respectively. The starting material was packed into a 2.2 mm outer diameter Au capsule and welded shut using a LAMPERT PUK 3 welding machine. Au is the most desirable capsule material to approach a closed system owing to its low hydrogen permeability59. The welded capsule was then squeezed into a cylinder of ca. 2.2 mm to minimize the thermal gradient. Based on a two-pyroxene thermometer60, the temperature gradient along the axis of the sample capsules was estimated to be <15 °C for both PC and MA experiments61. To ensure that the capsules were completely sealed, they were submerged in boiling water. Any capsule that released bubbles was assumed to have leaked and was hence discarded.
At 2.5 GPa, experiments were conducted in a half-inch piston-cylinder apparatus, using a pressure cell consisting of a straight graphite furnace + outer sleeve (Pyrex glass and talc) + inner MgO insert. A pressure correction of 13% was applied to compensate for friction effects based on a calibration of the quartz-coesite transition62. For the pressure range of 4–6 GPa, a multi-anvil device was used to compress the octahedral 25 mm edge-length tungsten carbide anvils with 15 mm corner truncations (the so-called 25/15 assembly). The pressure assembly consisted of a Cr2O3-doped MgO pressure cell, a straight lanthanum chromite heater, and MgO inserts (Supplementary Fig. 5a). The pressure was calibrated against the phase transitions of bismuth (Bi) metal at room temperature63, and of quartz to coesite62, and coesite to stishovite at 1000 °C64 (Supplementary Fig. 5b). The temperature was monitored and controlled by a type S (Pt-Pt90Rh10) thermocouple for piston-cylinder experiments, and type C (W95Re5-W74Re26) for multi-anvil experiments. The redox conditions during the experiments were controlled by the assembly and starting materials. The reaction of the graphite heater with the water released from the talc (for piston-cylinder experiments) yielded an oxygen fugacity close to the Ni–NiO (NNO) buffer65, whereas the lanthanum chromite heater (for multi-anvil experiments) should impose a higher oxygen fugacity than the NNO buffer. The recovered runs of both the piston-cylinder experiment and multi-anvil experiments usually contain magnetite, suggesting an oxygen fugacity lower than Magnetite-Hematite (MH) buffer. On this basis, the experiments had oxygen fugacity intermediate between the NNO and HM equilibria.
The run duration varied from 12 to 228 h, depending on the experimental temperatures. After the experiment, the recovered capsule was mounted in epoxy, ground longitudinally, and polished using a series of diamond pastes. Once exposed, the charge was impregnated repeatedly using a low-viscosity resin under vacuum conditions to minimize the losses of quenched liquids upon further polishing.
Identification of phases and analytical methods
The textures of the run products were identified from detailed studies of backscattered electron (BSE) images, and energy-dispersive spectra (EDS), collected with a 5-spectrometer JEOL JXA 8230 electron microprobe analysis (EMPA). Mineral phase compositions were determined by wavelength dispersive spectrometry (WDS) using the following standards: quartz for Si, corundum for Al, wollastonite for Ca, periclase for Mg, K-feldspar for K, albite for Na, magnetite for Fe, and MnO for Mn. The beam was set to a voltage of 15 kV and currents of 10 nA for phengite, 20 nA for other silicate minerals, 10 nA for silicate glass, and 6 nA for crystalline and quenched carbonates. The following beam diameters were employed: 1–5 μm for silicate minerals, 2–20 μm for silicate glass, and 2–10 μm for crystalline carbonates and quenched carbonates. The acquisition times for Si, Al, Ca, Mg, Fe, and Mn was 30 s on peak and 15 s on each background. To minimize the loss of Na and K, the acquisition times for both elements were 10 s on peak and 5 s on each background. Following the method of ref. 61 and ref. 66, the bulk compositions of quenched liquids were measured by energy-dispersive X-ray spectroscopy using an accelerating voltage of 20 kV, a beam current of 10 nA, and a counting time of 100 s. The use of energy-dispersive X-ray spectroscopy analysis enabled us to determine the average compositions of quenched liquids using apertures ranging from several microns up to hundreds of microns.
Data availability
All the data were listed in the online supporting information and Supplementary data files, and they are available at https://zenodo.org/record/7619742#.Y-NWzsjjwf4.
References
Galvez, M. E. & Pubellier, M. In Deep Carbon: Past to Present (eds Orcutt, B. N., Daniel, I. & Dasgupta, R.) Ch. 10 (Cambridge Univ. Press, 2019).
Kelemen, P. B. & Manning, C. E. Reevaluating carbon fluxes in subduction zones, what goes down, mostly comes up. Proc. Natl Acad. Sci. USA 112, E3997 (2015).
Plank, T. & Manning, C. E. Subducting carbon. Nature 574, 343–352 (2019).
Johnston, F. K. B., Turchyn, A. V. & Edmonds, M. Decarbonation efficiency in subduction zones: implications for warm Cretaceous climates. Earth Planet. Sci. Lett. 303, 143–152 (2011).
Kerrick, D. M. & Connolly, J. A. D. Subduction of ophicarbonates and recycling of CO2 and H2O. Geology 26, 375–378 (1998).
Kerrick, D. M. & Connolly, J. A. D. Metamorphic devolatilization of subducted oceanic metabasalts: implications for seismicity, arc magmatism and volatile recycling. Earth Planet. Sci. Lett. 189, 19–29 (2001).
Kerrick, D. M. & Connolly, J. A. D. Metamorphic devolatilization of subducted marine sediments and the transport of volatiles into the Earth’s mantle. Nature 411, 293–296 (2001).
Gorman, P. J., Kerrick, D. M. & Connolly, J. A. D. Modeling open system metamorphic decarbonation of subducting slabs. Geochem. Geophys. Geosyst. 7, Q04007 (2006).
Frezzotti, M. L., Selverstone, J., Sharp, Z. D. & Compagnoni, R. Carbonate dissolution during subduction revealed by diamond-bearing rocks from the Alps. Nat. Geosci. 4, 703–706 (2011).
Ague, J. J. & Nicolescu, S. Carbon dioxide released from subduction zones by fluid-mediated reactions. Nat. Geosci. 7, 355–360 (2014).
Robert, C. N. & Manning, C. E. Experimental determination of calcite solubility in H2O-NaCl solutions at deep crust/upper mantle pressures and temperatures: Implications for metasomatic processes in shear zones. Am. Mineral. 87, 1401–1409 (2002).
Caciagli, N. C. & Manning, C. E. The solubility of calcite in water at 6-16 kbar and 500–800 °C. Contribut. Mineral. Petrol. 146, 275–285 (2003).
Farsang, S. et al. Deep carbon cycle constrained by carbonate solubility. Nat. Commun. 12, 4311 (2021).
Poli, S. Carbon mobilized at shallow depths in subduction zones by carbonatitic liquids. Nat. Geosci. 8, 633–636 (2015).
Thomson, A. R., Walter, M. J., Kohn, S. C. & Brooker, R. A. Slab melting as a barrier to deep carbon subduction. Nature 529, 76–79 (2016).
Zhang, Y., Xu, Q., Wang, C. & Jin, Z. Release of CO2 in cold subduction zones by hydrous carbonatitic liquids. Geophys. Res. Lett. 48, e2021GL092550 (2021).
Hammouda, T. High-pressure melting of carbonated eclogite and experimental constraints on carbon recycling and storage in the mantle. Earth Planet. Sci. Lett. 214, 357–368 (2003).
Tsuno, K., Dasgupta, R., Danielson, L. & Righter, K. Flux of carbonate melt from deeply subducted pelitic sediments: Geophysical and geochemical implications for the source of Central American volcanic arc. Geophys. Res. Lett. 39, L16307 (2012).
Schettino, E. & Poli, S. In Carbon in Earth’s Interior (eds Manning, C. E., Lin, J.-F. & Mao, W. L.) Ch. 18 (Wiley, 2020).
Grassi, D. & Schmidt, M. W. The melting of carbonated pelites from 70 to 700 km depth. J. Petrol 52, 765–789 (2011).
Grassi, D. & Schmidt, M. W. Melting of carbonated pelites at 8–13 GPa: generating K-rich carbonatites for mantle metasomatism. Contribut. Mineral. Petrol. 162, 169–191 (2011).
Kiseeva, E. S., Litasov, K. D., Yaxley, G. M., Oh Tani, E. & Kamenetsky, V. S. Melting and phase relations of carbonated eclogite at 9–21 GPa and the petrogenesis of alkali-rich melts in the deep mantle. J. Petrol. 54, 1555–1583 (2013).
Dasgupta, R., Hirschmann, M. M. & Withers, A. C. Deep global cycling of carbon constrained by the solidus of anhydrous, carbonated eclogite under upper mantle conditions. Earth Planet. Sci. Lett. 227, 73–85 (2004).
Thomsen, T. B. & Schmidt, M. W. Melting of carbonated pelites at 2.5–5.0 GPa, silicate–carbonatite liquid immiscibility, and potassium–carbon metasomatism of the mantle. Earth Planet. Sci. Lett. 267, 17–31 (2008).
Poli, S. & Schmidt, M. W. Petrology of subducted slabs. Annu. Rev. Earth Planet. Sci. 30, 207–235 (2002).
Foustoukos, D. I. & Mysen, B. O. The structure of water-saturated carbonate melts. Am. Mineral. 100, 35–46 (2015).
Plank, T. & Langmuir, C. H. The chemical composition of subducting sediment and its consequences for the crust and mantle. Chem. Geol. 145, 325–394 (1998).
Mann, U. & Schmidt, M. W. Melting of pelitic sediments at subarc depths: 1. Flux vs. fluid-absent melting and a parameterization of melt productivity. Chem. Geol. 404, 150–167 (2015).
Martin, L. A. J. & Hermann, J. Experimental phase relations in altered oceanic crust: implications for carbon recycling at subduction zones. J. Petrol. 59, 299–320 (2018).
Mibe, K., Kawamoto, T., Matsukage, K. N., Fei, Y. W. & Ono, S. Slab melting versus slab dehydration in subduction-zone magmatism. Proc. Natl Acad. Sci. USA 108, 8177–8182 (2011).
Kawamoto, T., Kanzaki, M., Mibe, K., Matsukage, K. N. & Ono, S. Separation of supercritical slab-fluids to form aqueous fluid and melt components in subduction zone magmatism. Proc. Natl Acad. Sci. USA 109, 18695–18700 (2012).
Brey, G. P. et al. Reduced sediment melting at 7.5–12 GPa: phase relations, geochemical signals and diamond nucleation. Contribut. Mineral. Petrol. 170, 18 (2015).
Poli, S. Melting carbonated epidote eclogites: carbonatites from subducting slabs. Prog. Earth Planet. Sci. 3, 27 (2016).
Kono, Y. et al. Ultralow viscosity of carbonate melts at high pressures. Nat. Commun. 5, 5091 (2014).
Zhao, S., Schettino, E., Merlini, M. & Poli, S. The stability and melting of aragonite: an experimental and thermodynamic model for carbonated eclogites in the mantle. Lithos 324–325, 105–114 (2019).
Wyllie, P. J. & Boettcher, A. L. Liquidus phase relationships in the system CaO-CO2-H2O to 40 kilobars pressure with petrological applications. Am. J. Sci. 267, 489–508 (1969).
Nichols, G. T., Wyllie, P. J. & Stern, C. R. Subduction zone-melting of pelagic sediments constrained by melting experiments. Nature 371, 785–788 (1994).
Schmidt, M. W., Vielzeuf, D. & Auzanneau, E. Melting and dissolution of subducting crust at high pressures: the key role of white mica. Earth Planet. Sci. Lett. 228, 65–84 (2004).
Schmidt, M. W. & Poli, S. Experimentally based water budgets for dehydrating slabs and consequences for arc magma generation. Earth Planet. Sci. Lett. 163, 361–379 (1998).
Kessel, R., Schmidt, M. W., Ulmer, P. & Pettke, T. Trace element signature of subduction-zone fluids, melts and supercritical liquids at 120–180 km depth. Nature 437, 724–727 (2005).
Tsuno, K. & Dasgupta, R. Melting phase relation of nominally anhydrous, carbonated pelitic-eclogite at 2.5–3.0 GPa and deep cycling of sedimentary carbon. Contribut. Mineral. Petrol. 161, 743–763 (2011).
Skora, S. et al. Hydrous phase relations and trace element partitioning behaviour in calcareous sediments at subduction-zone conditions. J. Petrol 56, 953–980 (2015).
Presnall, D. C. An algebraic method for determining equilibrium crystallization and fusion paths in multicomponent system. Am. Mineral. 71, 1061–1070 (1986).
Yaxley, G. M. & Brey, G. P. Phase relations of carbonate-bearing eclogite assemblages from 2.5 to 5.5 GPa: implications for petrogenesis of carbonatites. Contribut. Mineral. Petrol. 146, 606–619 (2004).
Paterson, M. S. The melting of calcite in the presence of water and carbon dioxide. Am. Mineral. 43, 603–606 (1958).
Irving, A. J. & Wyllie, P. J. Subsolidus and melting relationships for calcite, magnesite and the join CaCO3-MgCO3 to 36 kb. Geochim. Cosmochim. Acta. 39, 35–53 (1975).
Durand, C., Baumgartner, L. P. & Marquer, D. Low melting temperature for calcite at 1000 bars on the join CaCO3-H2O – some geological implications. Terra Nova 27, 364–369 (2015).
Chen, C., Förster, M. W., Foley, S. F. & Liu, Y. Massive carbon storage in convergent margins initiated by subduction of limestone. Nat. Commun. 12, 4463 (2021).
Eguchi, J. & Dasgupta, R. Cycling of CO2 and H2O constrained by experimental investigation of a model ophicarbonate at deep subduction zone conditions. Earth Planet. Sci. Lett. 600, 117866 (2022).
Hudspeth, J., Sanloup, C. & Kono, Y. Properties of molten CaCO3 at high pressure. Geochem. Persp. Let. 7, 17–21 (2018).
Li, Z., Li, J., Lange, R., Liu, J. & Militzer, B. Determination of calcium carbonate and sodium carbonate melting curves up to Earth’s transition zone pressures with implications for the deep carbon cycle. Earth Planet. Sci. Lett. 457, 395–402 (2017).
Ritter, X. et al. Density of hydrous carbonate melts under pressure, compressibility of volatiles and implications for carbonate melt mobility in the upper mantle. Earth Planet. Sci. Lett. 533, 116043 (2020).
Skora, S. & Blundy, J. High-pressure hydrous phase relations of radiolarian clay and implications for the involvement of subducted sediment in arc magmatism. J. Petrol. 51, 2211–2243 (2010).
Schmidt, M. & Poli, S. Devolatilization during subduction. Treatise Geochem 4, 669–701 (2014).
Fumagalli, P. & Poli, S. Experimentally determined phase relations in hydrous peridotites to 6.5 GPa and their consequences on the dynamics of subduction zones. J. Petrol. 46, 555–578 (2005).
Spandler, C. & Pirard, C. Element recycling from subducting slabs to arc crust: a review. Lithos 170–171, 208–223 (2013).
Yaxley, G. M., Crawford, A. J. & Green, D. H. Evidence for carbonatite metasomatism in spinel peridotite xenoliths from western Victoria, Australia. Earth Planet. Sci. Lett. 107, 305–317 (1991).
Ammannati, E., Jacob, D. E., Avanzinelli, R., Foley, S. F. & Conticelli, S. Low Ni olivine in silica-undersaturated ultrapotassic igneous rocks as evidence for carbonate metasomatism in the mantle. Earth Planet. Sci. Lett. 444, 64–74 (2016).
Matjuschkin, V., Brooker, R. A., Tattitch, B., Blundy, J. D., & Stamper, C. C. Control and monitoring of oxygen fugacity in piston cylinder experiments. Contribut. Mineral. Petrol. 169, 9 (2015).
Mori, T. & Green, D. H. Subsolidus equilibria between pyroxenes in the CaO-MgO-SiO2 system at high pressures and temperatures. Am. Mineral. 61, 616–625 (1976).
Wang, J. et al. The water-saturated solidus and second critical endpoint of peridotite: implications for magma genesis within the mantle wedge. J. Geophys. Res. Solid Earth 125, e2020JB019452 (2020).
Bose, K. & Ganguly, J. Quartz-coesite transition revisited: reversed experimental determination at 500–1200 °C and retrieved thermochemical properties. Am. Mineral. 80, 231–238 (1995).
Decker, D. L., Bassett, W. A., Merrill, L., Hall, H. T. & Barnett, J. D. High‐pressure calibration: a critical review. J. Phys. Chem. Ref. Data 1, 773–836 (1972).
Ono, S., Kikegawa, T., Higo, Y. & Tange, Y. Precise determination of the phase boundary between coesite and stishovite in SiO2. Phys. Earth Planet. Inter. 264, 1–6 (2017).
Keppler, H., Wiedenbeck, M. & Shcheka, S. S. Carbon solubility in olivine and the mode of carbon storage in the Earth’s mantle. Nature 424, 414–416 (2003).
Adam, J., Locmelis, M., Afonso, J. C., Rushmer, T. & Fiorentini, M. L. The capacity of hydrous fluids to transport and fractionate incompatible elements and metals within the Earth’s mantle. Geochem. Geophys. Geosyst. 15, 2241–2253 (2014).
Buob, A., Luth, R. W., Schmidt, M. W. & Ulmer, P. Experiments on CaCO3–MgCO3 solid solutions at high pressures and temperatures. Am. Mineral. 91, 435–440 (2006).
Woolley, R. A. & Kempe, D. R. C. Carbonatites: Nomenclature, average chemical composition. In Carbonatites: Genesis andEvolution (ed. Bell, K.) 1–14 (Unwin Hyman, London, 1989).
Kiseeva, E. S. et al. An experimental study of carbonated eclogite at 3.5–5.5 GPa—implications for silicate and carbonate metasomatism in the cratonic mantle. J. Petrol. 53, 727–759 (2012).
Foley, S. F. et al. The composition of near-solidus melts of peridotite in the presence of CO2 and H2O between 40 and 60 kbar. Lithos 112, 274–283 (2009).
Dasgupta, R. & Hirschmann, M. M. Melting in the Earth’s deep upper mantle caused by carbon dioxide. Nature 440, 659–662 (2006).
Syracuse, E. M., Van Keken, P. E. & Abers, G. A. The global range of subduction zone thermal models. Phys. Earth Planet. Inter. 183, 73–90 (2010).
Ulmer, P. & Trommsdorff, V. Serpentine stability to mantle depths and subduction-related magmatism. Science 268, 858–861 (1995).
Acknowledgements
The authors thank Prelević Dejan and an anonymous reviewer, who provided a review with a lot of useful comments and constructive suggestions. Li Li, Xiaolin Xiong, and Eiichi Takahashi are acknowledged for their assistance with high-pressure experiments. This work was financially supported by the Strategic Priority Research Program of the Chinese Academy of Sciences (Nos. XDA22050101), the National Key R&D Program of China (Grant 2022YFF0801000), the National Natural Science Foundation of China (Nos. 91858206, 41888101, and 42003049), the Taishan Scholars Program of Shandong Province (No. tsqn201909157).
Author information
Authors and Affiliations
Contributions
W.C: methodology, validation, investigation, formal analysis, visualization, writing—original draft, and writing—review and editing. G.Z: conceptualization, validation, resources, funding acquisition, review, and editing. S.K: validation, review, and editing. Y.L: validation, review, and editing.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Communications Earth & Environment thanks Dejan Prelevic and the other, anonymous, reviewer(s) for their contribution to the peer review of this work. Primary Handling Editors: Maria Luce Frezzotti and Joe Aslin.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Chen, W., Zhang, G., Keshav, S. et al. Pervasive hydrous carbonatitic liquids mediate transfer of carbon from the slab to the subarc mantle. Commun Earth Environ 4, 73 (2023). https://doi.org/10.1038/s43247-023-00741-5
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s43247-023-00741-5
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.