The seasonal evolution of subglacial drainage pathways beneath a soft-bedded glacier

Abstract

Subglacial hydrology is a key element in glacier response to climate change, but investigations of this environment are logistically difficult. Most models are based on summer data from glaciers resting on rigid bedrocks. However a significant number of glaciers rest on soft (unconsolidated sedimentary) beds. Here we present a unique multi-year instrumented record of the development of seasonal subglacial behavior associated with an Icelandic temperate glacier resting on a deformable sediment layer. We observe a distinct annual pattern in the subglacial hydrology based on self-organizing anastomosing braided channels. Water is stored within the subglacial system itself (till, braided system and ‘ponds’), allowing the rapid access of water to enable glacier speed-up events to occur throughout the year, particularly in winter.

Introduction

Recent accelerated climate change has led to rapid glacier retreat, which is thought to be an important component of future sea level¹. An understanding of subglacial hydrology and sediment deformation are two key unknown elements in ice-sheet models^2,3,4; and it has been shown that the use of different sliding laws results in very different outcomes^5,6.

Most models of subglacial hydrology assume a hard bedrock system dominated by conduits, linked cavities and films^7,8. In these models, winter is characterised by an inefficient distributed system, with low surface velocities and generally high water pressures^9,10,11. In the spring, warming temperatures cause the meltwater input to be higher than drainage capacity, leading to water pressure rising higher than overburden pressure and resulting in basal sliding (the ‘spring event’) associated with the transition from one system to the other^12,13,14. Summer is dominated by high velocities, low water pressure and an efficient channelized system.

Recent research from Greenland has shown that in early summer whenever there are large surface melt events, water is able to reach the glacier base, leading to increased velocities via basal sliding¹⁵. However, by late summer, glacier velocity is no longer directly related to meltwater input because once the system is channelised, additional meltwater can be accommodated (self-regulation) by the subglacial hydrological system^16,17. This system drains both the ‘connected’ core areas which comprise efficient channels, and the ‘weakly connected’ areas comprising distributed drainage which surround it^18,19,20,21.

However, this model may not be universal. Glaciers resting on soft beds can have a different hydrology dominated by wide anastomosing broad flat channels, canals, macroporous films (at the ice/sediment interface) and porous flow through the till^22,23,24, resulting in a complex relationship between till water pressure, basal sliding and deformation^25,26,27,28. Much of this system has been characterized as an inefficient or distributed system^2,29, although numerous researchers^7,22 have argued that canals can be both efficient³⁰ and inefficient²³. This has potentially large ramifications because unconsolidated sediments are found beneath many of the fast-flowing ice streams of Antarctica and parts of Greenland, as well as in areas covered by the Quaternary ice sheets during previous glaciations^4,31,32,33.

The majority of studies (both field and theoretical) have concentrated on rigid-bedded glaciers, and how they have behaved during the summer. We present a rare instrumented multi-year, seasonal data set of a soft-bedded glacier, from which we reconstruct subglacial drainage patterns throughout the year. Each year, summer melt and rainfall represents only 60% of discharge. The excess water goes into storage within the subglacial system, where it is held within a wide and shallow anastomosing system of active and less active channels, as well as the macroporous layer and the till. In late autumn the number of channels decreases and the reservoirs become isolated. During winter, discharge represents almost five times the melt and rainfall, and on warm days when melting occurs, meltwater is rapidly transported to the glacier bed which leads to basal sliding, glacier uplift, till dilation and water pressure decline. This uplift of the glacier allows these subglacial reservoirs to be accessed, leading to a continued period of high drainage long after the melt-driven event has ceased, as well as a rearrangement of the drainage system until the next winter event occurs.

In spring, melt increases until it overwhelms the capacity of the winter drainage system, resulting in ‘Spring Events’, which are similar to the winter events, but which lead to the development of a new drainage system that is able to cope with the increased level of melt entering the system. As melt increases through the summer, so does the level of anastomosing, with resulting high water pressures, increasing accommodation of melt events, and the development of storage within the subglacial system itself. We highlight the similarities and differences between the Greenland (rigid-bed dominated) and the soft-bed model, in particular the rapid access of stored water in the soft-bed model allowing speed-up events throughout the year, which need to be considered in ice sheet models of glacier response to climate change.

Results

Field site

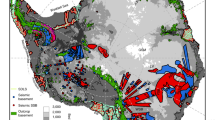
The study was undertaken at Skálafellsjökull, Iceland (Fig. 1), an outlet glacier of the Vatnajökull Ice Cap which rests on Upper Tertiary grey basalts. This glacier has an area of ~100 km² and is 25 km in length^34,35, with an elevation range between approximately 50 and 1490 m (m.a.s.l.). The study site was located on the glacier at an elevation of 792 m a.s.l., where the ice was flat and crevasse free. The subglacial meltwater in this instrumented area emerges 3 km away at the southern part of the glacier (Stađará river) and drains the southern part of the glacier known as the Sultartungnajökull catchment. The remainder of the glacier we have called Skálafellsjökull north for convenience. The glacier is resting on fine grain till with a mean grain size 53 µm. There is evidence of subglacial deformation in the foreland, with flutes and push moraines^36,37.

Fig. 1: Details of the field site.

a location within Iceland. b detail of Skálafellsjökull (field site shown with a box). Discharge measurement sites are shown; Stađará river time-lapse camera (star) and Kolgríma river gauging station V520 (circle). Glacier outlines from Randolph Glacier Inventory 6.0. Image is Sentinel-2 natural look colour composite from 30 August 2017.

Repeated Ground Penetrating Radar (GPR) surveys, combined with measured glacier depth, video recordings and borehole sampling, have shown that the glacier is resting on a till base, at least 1 m in depth with occasional small till-based cavities which were observed in 10% of the boreholes³⁵. The majority of the glacier has a mean radar velocity of 0.177 +/− 0.005 m ns⁻¹ (water content 0–0.5%) with a thin 1 m debris-rich basal ice layer with a radar velocity of 0.158 +/− 0.003 m ns⁻¹ (water content 2%)^35,38. From this it was shown that the glacier has little englacial storage, the ice is impermeable and drainage pathways are concentrated in fractures and moulins. Analysis of the basal reflectivity showed that the bed comprised three different components: water bodies cover ~6% of the area of the bed; a saturated deforming till bed covers 84%; and the remaining 10% comprises an undeforming bed, comprising bedrock, frozen till, low porosity till, lake sediments, outwash sand and gravels^35,37. During the summer, it was shown that water bodies comprise of a series of braided channels with a typical width of 0.5–15 m (mean 3 m) with the velocity from one channel measured at >0.1 m s⁻¹ with a depth of 2 m³⁶.

Field data were collected between summer 2008 and autumn 2014, with a continuous discharge record 01/01/2008–31/08/2010 and remote sensed imagery between 06/06/2017 and 24/09/2019. Field data was collected via the Glacsweb environmental sensor network³⁶ which comprised in situ sensor nodes (probes) in the till, base stations and a sensor network server in the UK, as well as GPS and discharge measurements. The Glacsweb probes (0.16 m long) contained micro-sensors measuring water pressure, probe deformation, resistance, tilt and probe temperature. Eight probes, three in the ice and five in the till, sent back between 74 and 397 days of data and details of sensors, readings, locations and errors are discussed elsewhere³⁸. Here we discuss the water pressure results, measured in metres water equivalent (mW.E.) (hydraulic head) and expressed as a percentage of glacier thickness (mW.E./h%), and case stress (kPa), from two probes in the till, probe 21 (autumn and winter 2009/10) and probe 25 (summer 2010).

Details of the data sets and uncertainty are outlined in the ‘Methods’, some of which have discontinuous records due to logistical problems with field data collection including power, connectivity, equipment availability and light levels. However, there is sufficient data similarity, correlation and overlap between the different years to enable the estimation of data patterns during any data gaps (discussed below) and allow the reconstruction of the overall seasonal pattern.

Seasonal patterns

We define the seasons based on the melt rate³⁹. Winter is identified as the time when there is no melt, apart from a series of warmer days when temperatures rise above zero, which are known as positive degree days; and the melt season as the time when melting occurs. The melt season is divided into three sub-seasons. Spring is a time of low melt where the majority of days have less than the 10% of mean melt season melt; summer is marked by a high melt; and autumn reflects a distinctly lower level of melt, <33% of the mean melt season melt level, often with air temperatures falling below zero at night (Fig. 2). We also calculate the component of precipitation that falls as rain (see ‘Methods’), which was ~20% of the total inputs.

Fig. 2: Long-term records.

a Skálafellsjökull north—Till water pressure, case stress, daily discharge from the component of the Kolgríma river from this part of the glacier (see the ‘Discharge’ section in ‘Methods’ for detail) and daily air temperature—2009/10. b Sultartungnajökull catchment—mean horizontal surface velocity, daily discharge (Stađará river) and daily air temperatures—2009/10. c Skálafellsjökull—mean velocity along the flowline (Sentinel-1 Remote sensed data) and daily air temperature 2017/18. Calculation of error explained in ‘Methods’, in the ‘Measurements of ice velocity’ section. All daily air temperatures from the base station, DOY = day of year.

We show three long-term records reflecting the most extensive data sets. In 2009/10, we collected in situ till water pressure and case stress (till strength) and discharge and air temperature at the base station (Fig. 2a). As water pressure increases the case stress decreases, as it scales with effective pressure (ice overburden pressure minus pore water pressure in the till). An extended data set of Skálafellsjökull north inputs (melt and rainfall) and outputs (the proportion of Kolgríma river discharge) from Jan 2008 to August 2010 is provided with the data files, which shows a similar pattern to Fig. 2a. In 2012–14, we have surface horizontal and vertical (not shown) GPS velocity, discharge and melt (Fig. 2b). Glacier uplift (based on the GPS data) has already been reported³⁷, and is shown for cycle 3 for comparative purposes. In 2017/18 we have remotely sensed velocity (12-day repeat) and air temperature data (Fig. 2c).

Where discharge data is available, we are able to show the relative inputs (mean daily melt and rain) and outputs (mean daily discharge) for each season (Fig. 3). Although there are some annual variations, the general pattern for each season is similar. During the spring, mean daily discharge is relatively similar to the average daily inputs, mean discharge 107% of inputs (s.d. = 31%), mean total input 30.3 × 10⁵ m³ s⁻¹ (s.d. 19.2 × 10⁵ m³ s⁻¹), mean total output 30.0 × 10⁵ m³ s⁻¹ (s.d. 15.1 × 10⁵ m³ s⁻¹). During the summer, mean daily discharge only accounts for 60% (s.d. = 20%) of the mean daily input, %), mean total input 124.8 × 10⁵ m³ s⁻¹ (s.d. 53.5 × 10⁵ m³ s⁻¹), mean total output 79.7 × 10⁵ m³ s⁻¹ (s.d. 46.2 × 10⁵ m³ s⁻¹). In winter, mean daily discharge far exceeds mean daily input, mean 499% (s.d. = 48%), mean total input 8.9 × 10⁵ m³ s⁻¹ (s.d. 7.7 × 10⁵ m³ s⁻¹), mean total output 20.7 × 10⁵ m³ s⁻¹ (s.d. 12.6 × 10⁵ m³ s⁻¹). In autumn the mean discharge is similar to the inputs, mean discharge 99% (s.d. = 88%) of inputs, mean total input 119.8 × 10⁵ m³ s⁻¹ (s.d. 135.6 × 10⁵ m³ s⁻¹), mean total output 83.0 × 10⁵ m³ s⁻¹ (s.d. 93.8 × 10⁵ m³ s⁻¹).

Fig. 3: Mean daily inputs (melt and rain) and discharge per season.

Where a full record for discharge was not available (shown with hatching), the percentage days of the record are shown. Data for 2008–2010 for Skálafellsjökull north, 2012–14 Sultartungnajökull catchment. The calculation of error is explained in ‘Methods’, in the ‘Melt estimate’ and ‘Discharge’ sections.

Autumn

At the beginning of autumn water pressures in the till are high, but then begin to fall as the melt level decreases, e.g. DOY (day of year) 263 in 2009 (Fig. 2a), while case stresses correspondingly rise. The discharge mirrors the melt over the season, and on a diurnal scale, air temperatures and discharge tend to peak at midday and decline overnight.

Autumn has some of the highest recorded peak velocities, defined as 98% percentile, but the mean daily velocity is less than summer. For the 2012 and 2013 data, the mean autumn velocity was 9.4 m a⁻¹, and the mean summer velocity was 12.0 m a⁻¹. The peak velocities coincide with the high melt events (Fig. 2b).

Winter

During the winter, daily average temperatures drop below zero so there is little melting on the glacier surface, apart from a series of ‘warm’ days observed as positive temperatures at the base station and high surface melt. Days with high melt are marked by a small sharp rise then by a dramatic drop in till water pressure over a mean 5 h period of 1.77 m W.E.% glacier depth per hour, followed by a slow rise in water pressure until the next event. At the same time, discharge dramatically increased as melt increased, normally reaching a peak one day after the melt peak, with continued high discharge for 4–6 days afterwards (Fig. 2b).

When temperatures were below zero there was a low base velocity with relatively high-velocity peaks during positive degree days (Fig. 2b). During the speed-up events, glacier surface horizontal velocities were up to 500% faster than the base level winter horizontal velocity, and lasted between 1–4 days. At the same time, there was vertical uplift of the glacier (Fig. 4), followed by an increase in discharge (outlined below).

Fig. 4: Detail of winter cycle 3 (2012).

This data is from the Sultartungnajökull catchment with the different phases shown (see Fig. 2b for reference). An estimated till water pressure record, reconstructed from 2009/10 warm events, is shown for comparison.

Associated with the speed-up events will be shearing of the till, which may result in a cycle of dilation and compaction^40,41. Prior to the melt input the till may be compacted. The burst of meltwater from the melt event may cause the till to dilate and water pressure to initially decrease, causing more surrounding water to flow into the till. As the glacier velocity decreases, till compaction occurs and there is excess discharge from the till.

The relationship between the different parameters is shown for one cycle from 2012 DOY 329–362 (Fig. 4). This includes an estimated till water pressure record, reconstructed from the 2009/10 data. This was calculated by using the mean water pressure maxima prior to the warm events (80.8 m W.E.% glacier depth), the mean initial rise (3 m W.E.% glacier depth), and the mean rate of water pressure decrease and increase associated with each cycle which was shown above. Each cycle consists of the following phases: Phase (I) low or little melt, with air temperature below zero, for 3–25 days, associated with low discharge, a base winter velocity, rising till water pressure, till compaction; Phase (II) melt event, causing an increase in discharge, and surface horizontal velocity, small rise and then substantial decrease in till water pressure and glacier uplift resulting from a combination of shear-induced till dilation and bed separation; Phase (III) temperatures return to below zero, so melt returns to a low level and velocity returns to a base level, the glacier reconnects with the bed, till water pressures start to rise, however, the discharge remains high for several days; Phase (IV) discharge falls for 1 day to an intermediate level before returning to Phase I conditions. Specific details of the 2012/13 cycles are shown in Table 1.

Table 1 Daily properties of the discharge cycles during winter 2012/13.

In order to understand the relationship between input (melt and rainfall), storage and discharge we modelled the behaviour using a simulation of discharge, which is discussed in the ‘Methods’, using the parameters derived from Table 1. The measured discharge and simulation model are very similar with a root mean squared error of 0.89. From this model we can estimate the relative components of the winter discharge: (i) 29% is from surface melt and rain; (ii) 19% comes from the heat generated from movement, englacial flow and water released from till compaction, calculated by discharge minus melt and rain during phase I; (iii) 52% is from the winter event driven subglacial storage release, discharge minus melt during phases II–IV. This latter category may include additional shear heating and melting associated with phase II. This shows that the melt-driven events are not a minor phenomenon, but a major part of the subglacial hydrology.

Spring

The discharge data for spring 2008–2010 (diurnal) and 2013 (4 hourly) show a similar pattern (Figs. 2a, 5a, b). There is a slow rise in discharge during early spring, with a mean of 16.75 days, followed by a rapid discharge rise of 117%, lasting 1–2 days. This latter event does not appear to correlate with any specific high melt/temperature events. Afterwards, the discharge was consistently high, even at night, and continued to increase even though temperatures were falling. This phase lasted a mean of 3.5 days. Then the trend in temperatures and discharge were similar and a diurnal pattern returned. We suggest the dramatic rise in discharge marks the spring event, and the return to a positive relationship between air temperature and discharge with a diurnal pattern indicating the beginning of summer. There is also a strong relationship between the date of the beginning of spring and the date of the spring event (r² = 0.99).

Fig. 5: Changes in discharge, velocity and air temperature during spring for the Sultartungnajökull catchment.

a Daily discharge during 2010 from the component of the Kolgríma (see ‘Methods’ for detail). Spring begins DOY 123, spring event DOY 139, summer begins DOY 145. b Daily discharge during 2013, spring begins DOY 128, spring event DOY 144, summer begins DOY 148 (calculation of error explained in the ‘Discharge’ section in ‘Methods’). c Twelve-day velocity 2018 (this data has been scaled to the GPS data for comparative purposes, see ‘Methods’ for details). Spring begins DOY 128, spring event approx. DOY 143, summer begins DOY 149. d Twelve-day velocity windows 2019. Spring begins DOY 133, spring event approx. DOY 148, summer begins DOY 154.

We can also investigate how the velocity changes over the spring from the velocity patterns for 2018 and 2019 (Figs. 3c, 5c, d). We have shown above that the spring event cannot be identified by the melt/temperature pattern alone, however, because we have determined a relationship between the beginning of spring and the spring event, we can predict the date. In 2018 this would be approximately DOY 148 and in 2019 DOY 157.

In both 2018 and 2019, the early spring velocities were quite similar to peak winter velocities. The spring event can be identified by a distinct rise in velocity close to the predicted date, with an increase in velocity of 16% in 2018 and 35% in 2019. The magnitude of the spring event in both years, was in the upper part of a range when compared with the peak winter velocities. In 2018 it was 5.5% above the mean and in the 70% percentile, in 2019 it was 20% above the mean and in the 85% percentile.

Summer

Summer is characterized by high melt, discharge, velocity and water pressure (Fig. 2). The 12-day velocity data was compared with the 12-day mean air temperature for the same periods for summer 2017–2019, as well as the average discharge for eight equal periods during the summers of 2008 to 2010 (Fig. 6).

Fig. 6: Summer data.

Mean 12-day summer scaled velocity data against 12-day daily mean air temperatures for summer 2017–19, and mean 12-day scaled discharges for summer 2008–2010 (Skálafellsjökull) (error bars represent the standard deviation of the 2-year data set).

Each summer can be divided in two parts. The early part of the summer, e.g. DOY 144–181 in 2010, has relatively constant till water pressure, with a positive relationship between melt and discharge (r² = 0.66). This period is characterized by a low discharge, with the highest velocities, e.g. DOY 170 in 2018, increasing by 28% above the summer mean, and by 18% above the velocities observed during the spring event.

During the middle to late summer, e.g. DOY 182–257 in 2010, there is change to higher melt and discharge, and a pattern of sharp declines followed by slower rises in water pressure. In all the summers (2008–10), some of discharge peaks occurred after some, but not all of the large melt events. In 2010, the two large declines in water pressure occur associated with the largest discharge peaks (DOY 189 and 215). The first event, DOY 194 in 2010, occurs after a period of low temperatures; and the second DOY 213 in 2010, after a sustained period of high melt. We assume these events are also accompanied by speed-up, although we have no velocity data for this period.

The 12-day velocity data showed the velocities were lower during middle and late summer even though this was the time of highest air temperatures, with a small rise in velocity towards the end of summer (Fig. 7). Daily surface velocity data from middle and late summer i.e. DOY 214–252 in 2012 and DOY 200–234 in 2013) showed there was no significant relationship between melt and surface velocity (r² = 0.03) (Fig. 2b). However, the highest and lowest daily velocities tended to coincide with, or occurred the day after, the highest and lowest melt events (Fig. 2b).

Fig. 7: Summary annual record.

Skálafellsjökull composite storage (melt and rain minus discharge), till water pressure, and discharge from 2009/2010 data, velocity data estimated based on data from other years.

Annual pattern of change in storage, till water pressure, discharge and velocity

The data collected from the different years allows us to reconstruct the annual pattern of storage (melt and rain minus discharge, per day⁴²), water pressure in the till and velocity over a schematic year, beginning in autumn, for the whole glacier (Fig. 7). We have used the discharge, melt and till water pressure from 2009/10. We have shown above that the velocity has a distinct pattern related to air temperature, and so we have been able to reconstruct a velocity record for 2009/10. The summer is characterized by positive net storage, high till water pressures, with highest mean velocities in early summer, highest melt and discharge in middle and late summer, with melt-related speed-up events. Winter is characterized by melt-driven events which cause a fall in till water pressure, rise in velocity and negative storage events (evacuation). During autumn there is a decrease in till water pressure and storage, and very high velocities related to melt. During the spring, the spring event is not related to a specific melt event, but produces a large discharge and velocity rise, similar to the winter high velocities. The storage is generally positive during early spring, and then negative associated with the spring event with a general overall balance.

Discussion

There is an emerging picture of soft-bed subglacial hydrology, although much of this is theoretical rather than instrumented. It has been argued^43,44,45 that soft-bed subglacial hydrology develops in three stages in response to rising meltwater inputs. At low melt levels water is stored within the till, but once the till becomes saturated, meltwater will accumulate at the ice/till interface in a sheet (macroporous layer). At higher melt inputs, rills will form which can grow into shallow streams. Rills typically form anastomosing or braided water courses. It has been suggested that a braided river system was present beneath Storglaciären²² and that the degree of anastomosing changed with discharge levels throughout the season. Similarity experiments carried out to simulate a pressurized braided subglacial flow under plate glass⁴⁶, have shown that as discharge increases the system reorganizes and the degree of braiding intensifies, with a main channel dominant at the highest discharge. As the discharge decreases, water may become isolated from the main channels in unconnected elements, ‘sloughs’ or ‘ponds’. This is important as the soft-bed hydrological system beneath West Antarctica has been described as ‘swampy’^31,44, ‘distributed’⁴⁷ or ‘water-saturated wetlands’⁴⁵. The latter suggest that the macroporous layer or film, generates a spatially heterogeneous drainage system by eroding the sediment below. It has been reported that beneath Thwaites glacier there is a mixed bed, comprising rigid bed dominated subglacial highlands at the margin, with deep channels⁴⁸ and an upstream soft-bed dominated sedimentary basin, which mostly comprises soft-bed with pooled water⁶.

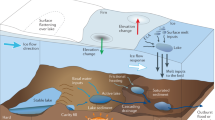
We suggest that our data from Skálafellsjökull provides evidence for a soft-bed hydrological system; porous flow within the till, reflected by changing in situ till water pressures and a wide shallow anastomosing system, reported by GPR evidence. Our data provide an instrumented record to corroborate the models discussed above. We now propose how this model can explain seasonal behaviour observed at the site (Fig. 8).

Fig. 8: Model of the seasonal changes associated with subglacial anastomosing drainage.

a Summer drainage. An active braided system with both main and subsidiary channels, with the level of anastomosing related to surface melt, with water moving slowly into storage within the subglacial system because inputs are greater than discharge. b Spring drainage. c Autumn drainage. During spring and autumn most water flows in the main channels, and in autumn some water becomes isolated in small reservoirs. d Winter drainage. During negative degree days, discharge is very low. During the positive degree days, there is high discharge associated with surface meltwater and water being evacuated from subglacial storage, which will travel along the main channels.

During autumn the meltwater input gradually reduces and becomes less than the discharge. The level of anastomosing is reduced, and water flow is concentrated along the main channels (Fig. 8c). Water may become isolated from the main channels in the unconnected elements and ‘ponds’ form. At the same time, water drains out of the till, which is reflected by the falling water pressures and increasing case stress. The water pressures decrease in line with falling melt. We suggest that high peak velocities of the year occur at this time because the relatively high melt exceeds the carrying capacity of the subglacial hydrological system, which leads to reduced effective pressure at the bed resulting in speed-up events^{8,42,49,50,51}.

Winter is characterized by two contrasting behaviours related to surface melt. For most of the winter temperatures are below freezing and there is a low base velocity and discharge. In contrast, during positive degree days, surface melt is produced. This results in glacier speed-up, shear-induced till dilation, glacier uplift and high discharge. This is followed by a slow water pressure rise and till compaction until the next melt event.

The resultant discharge in winter is far greater than the associated meltwater input. To produce the pattern observed, we showed from our modelling experiments that during cooler days, the small amount of melt generated by basal friction and release from the till associated with compaction is added to local storage, i.e. cavities or macroporous storage. During the positive degree days, the meltwater itself is released, along with the incremental storage generated since the last melt event, plus an additional element which is most likely sourced from the longer term, probably summer, storage. The source of this output are the numerous other subglacial reservoirs, including cavities, macroporous sources and the ponds, which become ‘connected’ during glacier uplift, as water can travel at the ice/till interface into the active channels (Fig. 8d). This will include canals that are incised into the bed, which require less energy than r-channels and are increasingly stable at lower effective stresses on the bed⁵². This resultant ‘flood’ makes a new drainage pattern, which continues until the next melt event. This increased drainage takes four to 6 days to drain back to the original level.

With the onset of spring, the daily melt rate increases, water pressures rise, and the subglacial system supports a relatively stable discharge with a diurnal cycle. We see a dramatic rise in discharge, which marks the spring event, which is accompanied by a speed-up event^12,42,49. The magnitude of this event was similar to that of the larger winter events, however, unlike the winter events, our spring events were not directly driven by a specific melt event. We suggest that during early spring, ~17 days in duration, the increasing melt is accommodated within the main winter channels (Fig. 8b). However as the melt increases, it eventually overcomes the system, resulting in the spring event, and in a similar way to a winter melt event, water is released from storage and a new drainage pathway develops. This high discharge continues to drain the newly connected areas for 4–5 days, subsequently, the discharge pattern reflects surface melt, so we suggest that the new hydrological system is now adapted to the new, higher, summer input level.

During summer we suggest that there is an active braided system with both main and subsidiary channels, with the level of anastomosing related to melt. At the beginning of summer, the channels are opening and there is direct flow along the main channels with the beginning of increasing anastomosing as relative melt increases. There is a positive relationship between increased melt, discharge and velocity. However, later in the summer, most increased melt is absorbed by the hydrological system via the increased anastomosing and meltwater transport capacity, and so overall velocity decreases, although daily velocities respond to melt. However, when inputs exceed the carrying capacity of the system, the storage systems are temporarily overwhelmed, which leads to reduced effective pressure at the bed resulting in speed-up events, till water pressure decrease and water release.

Over the summer as a whole, there is a greater input of water to the system than is output and so additional daily melt is forced to go into storage; in cavities in the ice, the debris-rich basal ice, the till, the macroporous layer and the braided system itself. Reports of net storage in summer are rare: one study of subglacial storage from Isortoq glacier, Greenland showed that discharge only represented 37–75% of melt season melt⁵³.

We suggest the following similarities and differences between the ‘Greenland’ hard-bed dominated and our soft-bed dominated model. Both models show high velocity in early summer resulting from direct meltwater imports, with decreasing velocities over late summer as the subglacial hydrology accommodates the water. In Greenland this is due to early summer channelization and late summer increase in a distributed system alongside the channels, comprising linked cavities, with a low hydraulic conductivity covering 66% bed^17,18. In the soft-bed example, this is due to increased anastomosing throughout the summer. This results in high till water pressures and high water storage in the subglacial hydrological system itself, with annual discharge representing 70–100% of annual melt.

Both systems also have speed-up events, when meltwater inputs are higher than the drainage capacity, which results in reduced effective pressure and sliding at the bed. In Greenland this typically happens in spring and autumn⁵⁴, while at Skálafellsjökull this occurs in all seasons. This is because the soft-bed hydrological system has such high and easily accessible storage capacity, so that whenever a speed-up event occurs (particularly in winter) water can be rapidly accessed which has a dramatic effect on the glacier and drainage system.

We have developed a model for subglacial hydrology associated with soft-beds derived from an Icelandic glacier, and have suggested this model may have similarities with the fast-flowing ice streams of West Antarctica. The next steps would be to investigate whether this model is applicable to other soft-bed glaciers in Iceland and elsewhere, to examine in detail the water flow within the tills, and investigate the implications of this hydrological system on glacier stability in response to climate change.

Methods

Glacsweb probes

In order to insert probes into the till, boreholes, 57−69 m deep, ~0.1 m diameter, were drilled to the base of the glacier with a Kärcher HDS1000DE jet wash system and the presence of till was examined using a custom-made digital infrared LED-illuminated colour video camera, via the borehole. If till was present it was hydraulically excavated⁵⁵ by maintaining the jet at the bottom of the borehole for an extended period of time. The probes were then lowered into this space, enabling the till to subsequently close in around them. The depth of the probes within the till was ~0.1−0.2 m beneath the glacier base, estimated from video footage of the till excavation prior to deployment. The probe data were recorded every hour, and transmitted to the base station located on the glacier surface. These data were sent daily via GPRS to a web server in the UK³⁸.

These water pressure data were calibrated against the measured water depths in the borehole immediately after probe deployment. The glacier thickness (h) was determined from measuring the depth of the boreholes and comparing with the GPS data of the glacier surface. The case stress represents the force applied to the probes per unit area and was measured by strain gauges that measured the relative compression and extension of the probe case in two perpendicular planes. This was calibrated using an Instron 5560 tension/compression experimental machine with a nitrogen-cooled chamber, which operated at a mean temperature of 1.3 °C.

The probes were designed so that if the data were not immediately accessed then they were stored for later retrieval. There were some problems with communications between the probes and the base station which unfortunately led to the probes filling their programmable memory (EPROM), resulting in some data gaps.

Melt estimate

Temperature data was measured at the glacier base station (+/−0.6 °C) and sent back to the UK with the probe data each day, and also at the Icelandic Meteorological Station at Hofn, 30 km away at sea level. The measured lapse rate between the two locations is 0.0082 °C m⁻¹, using data from the 451 days between August 2011 and July 2014 when the base station temperature sensor was not covered with snow. This was used to estimate temperature across the glacier, using the Global ASTER digital elevation model (ASTER GDEM). The altitude of the snow line was estimated from the MODIS daily albedo data, with interpolation where necessary, taking the threshold between ice and snow to be 0.45. We calculated the melt estimate over two areas; the full glacier, based on the standard Icelandic glacier catchments³⁴, and smaller area that drained that Sultartungnajökull catchment (Fig. 1b) was calculated by the degree-day algorithm⁵⁶, using degree-day factors for Satujökull, Iceland: 5.6 mm d⁻¹ °C⁻¹ for snow and 7.7 mm d⁻¹ °C⁻¹ for ice⁵⁷. All calculations were carried out on the 30 m × 30 m grid of the ASTER GDEM.

We are able to compare our melt calculations with measured ablation during the field season. Measured mean ablation in 2008, over a 12-day period from 11 stakes, was 0.036 m d⁻¹, compared with a calculated value of 0.033 m d⁻¹ over the same period, and in 2011 the measured mean ablation, over an 11-day period from 15 stakes, was 0.047 m d⁻¹ compared with the calculated value of 0.044 m d⁻¹. This shows that the calculated ablation depths were 8% lower than the measured results, so although possible sources of error include the degree-day factors, albedo and lapse rate, our calculated melt is within an appropriate level of uncertainty with independent field results.

Measurements of ice velocity

Surface ice velocity was measured from 2008 to 2012 with a TOPCON Legacy-H L1/L2 GPS (1 km baseline) and from 2012 to 2013 with an additional array of 4 dual frequency Leica System 1200 GPS systems at 15 s sampling rate, continuously during the summer and 2 h a day during the winter (300 m baseline). The GPS data was processed with the ephemeris from the International GPS Service (IGS) stations using TRACK (v. 1.24), the kinematic software package developed by Massachusetts Institute of Technology (MIT) http://geoweb.mit.edu/~tah/track_example/). We derived an average surface horizontal velocity by taking the mean of 4 GPS stations to remove local variations. To account for surface melting, we removed the daily melt from the vertical measurements. The error estimates were as follows (sigma per day): mean North +/− 0.0045 m, mean east +/− 0.0032 m, mean height +/− 0.0092 m.

The glacier uplift of the surface ice was calculated using the established Anderson method^37,58, this method isolates the uplift (combined bed separation and till volume changes) from the downward vertical component of mean bed-parallel motion, thinning or thickening of ice associated with ice strain.

We also calculated surface velocity from Sentinel-1 SAR imagery with a 12-day repeat cycle to show how velocity changed over the whole year (2017–2019). Velocity data was generated using the intensity tracking algorithm within the European Space Agency (ESA) Sentinel Application Platform (SNAP). Intensity tracking is less precise than interferometry but given the high temporal correlation of glacier surfaces, is much more robust⁵⁹. Each pair of SAR images were calibrated and co-registered together using a Digital Elevation Model (DEM)-assisted co-registration based on an airborne LiDAR DEM provided at 5 m resolution from the Icelandic National Land Survey. Velocities were then calculated using cross-correlation with a 5 × 5 moving window and a search distance of 64 pixels. Any displacements that had a cross-correlation threshold lower than 0.01 were removed, and the displacements were averaged to a 5 × 5 mean grid and converted to ground range resulting in velocity rasters at 10 m resolution. The stochastic error in our velocity measurements was assessed by measuring displacements over terrain that we regarded as stable^60,61. The average RMSE for the Sentinel-1 imagery over the entire period was +/−0.15 m per day. Mean velocities and errors were then calculated along the centre line (Figs. 1b and 6).

A previous study³⁶ compared the known annual surface velocity measurements (2012/2013) from the 5 GPS (V_GPS) stations with compared with the same points on remote sensed imagery for the whole glacier (TerraSAR-X 2012 data) (V_RS). The two gave a very strong positive correlation with an r² of 0.998, enabling us to calibrate the mean velocities along the centre line using the following relationship:

$${V}_{{{{{{{\rm{GPS}}}}}}}}=\left(0.560\times {V}_{{{{{{{\rm{RS}}}}}}}}\right)+1.888$$

(1)

The study also showed there was a strong relationship (r² = 0.98) between glacier depth and velocity, so we could use this relationship to scale down the calibrated centre line velocities to a similar depth to the averaged GPS velocity data for comparative purposes.

Discharge

We attained two sets of discharge data from different time periods. The first was from the outlet river at the Sultartungnajökull tongue and was collected using a time-lapse camera mounted on a bridge (Fig. 1b) on the Stađará river, 23rd September 2012 to 16th July 2013 and 28th July 2014 to 4th October 2014. The discharge estimates took place close to the glacier margin, and reflected water from the Sultartungnajökull catchment. The camera was a Brinno TLC100, an inexpensive time-lapse camera designed for unattended outdoor battery-powered operation. It could capture up to 28,000 frames of 1280 × 1024 pixels, and had a fixed field of view of ~50° on the diagonal. Five main sequences were recorded: (i) at one-minute intervals from 23 to 26 September 2012 (DOY 267–270), which was analysed at 15 min intervals; (ii) at 4-h intervals from 22 October 2012 (DOY 296) to 6 June 2013 (DOY 157); (iii) a single hand-held image from the same location (16th July 2013, DOY 197); (iv) at 20 min intervals from 27th July 2014 (DOY 209) to 1st August 2014 (DOY 213); v) 4-h intervals from 2nd August 2014 (DOY 214) to 4th October 2014 (DOY 277). In all cases, images were missing when the light level was too low for effective capture or mist blocked the scene. For a substantial part of the second sequence, the course of the river was covered with snow. In addition, there was no data collection between July 2013 and July 2014 due to battery failure.

Estimates of discharge were made by fitting a model of the river bed to the boundary of the water surface in each image, using automatically-detected edges with manual supervision⁶². We then applied the Glauckler-Manning equation to the same model. We used a combination of two methods⁶³ to estimate the roughness coefficient n; (i) a visual method from pictures of measured sites⁶⁴ and (ii) a composite calculation using modifying values from a base value⁶⁵. Using the visual method we found 3 images that were most similar to our site, which had a measured mean n value of 0.060 (s.d = 0.008). We then used the composite method to evaluate the three images, which overestimated n by 4.5%. We then used the composite method to find an n value for Skálafellsjökull and reduced this value by 4.5%. This resulted in an n value of 0.060 which was very similar to the visual method. We used this value, with the estimated flow cross-section, to compute discharge. To overcome the problem of different sampling rates throughout the season, because of different light levels, we resampled the 24 h data at shorter intervals to produce correction factors which we were able to apply to the data.

Random errors were estimated by using multiple measurements from different parts of the scene, and were used to remove inconsistent discharge estimates from the time series (>2 s.d.). This resulted in an estimated error of 0.21 m³ s⁻¹ (shown in Figs. 3 and 5). There are a number of factors that may affect the uncertainty of the results, peak discharges may be underestimated using the Manning equation due to the fact that flow is highly variable and the relative roughness is going to be highly variable as well, alternatively the observed cross-section may be partly obscured by snow leading to an potential overestimation of discharge. There was mitigation to avoid the later problem, as the technique is only semi-automatic, and so any outliers particularly the large winter discharges were manually checked. This time-lapse camera method has now also been successfully used by other researchers⁶⁶.

The second data set was from the Icelandic Meteorological Office gauging station V520 providing a mean daily reading which was operational during our study period from 1st January 2008 to 31st August 2010 (Kolgríma river) (Fig. 1b). This provided data for 97% of the days, of which 75% of the data was classed as good and 25% as estimated. The estimated data followed the same pattern and magnitude as the good data. Assuming the good data has an error of 5% and the estimated an error of 10%, this would result in an overall error of 6.2% (shown in Fig. 3). This gauging station was located on the Kolgríma river and measured the discharge from three components; Skálafellsjökull north as well the adjacent Heinabergsjökull and the non-glaciated parts of the catchment.

We derived the component from the non-glaciated catchment in two ways. The first was to assume the runoff from the non-glaciated catchment would be equal to its area multiplied by a runoff coefficient. Using a runoff coefficient calculated from Iceland as a whole⁶⁷ (0.83 for Iceland), this resulted in a discharge of 1.09 × 10⁶ m³. The second method was to assume the measured winter base discharge from the Kolgríma river reflected the discharge from the non-glaciated area (Fig. 2a) 1.10 × 10⁶ (s.d. = 3.41 × 10⁴) m³ with the uncertainty calculated from variation in the base discharge. The results from the two methods are remarkably similar, and so we used the measured base discharge.

The discharge from each glacier would comprise the melt, the rain and frontal melting from the proglacial lake. The lake melt was calculated by estimating the annual marginal ice loss from 2009 ERS-2 image, and 2012 TerraSAR-X image. For each image the lake boundary was digitized 10 times and then the standard error was calculated as +/−0.001 to 0.002 km².

We used the positive degree algorithm to determine the melt for Heinabergsjökull for 2009/10, using the method described above. The rainfall contribution for both glaciers was calculated by estimating the amount of precipitation that falls as rain over the snow-free glacier area. We used a mean annual rainfall correction factor of 1.28⁶⁸ to the Hofn weather station rain gauge data, used the results from the linear theory model of orographic precipitation for Iceland 1958–2006^69,70 to calculate changes in precipitation with altitude, and used a constant snow/rain threshold at 1 °C⁵⁴. Sources of error include area measurement (+/−0.1 m²)^69,70, annual correction factor and altitudinal linear theory model (+/−1.5 mm)^69,70. This resulted in the following breakdown of the different components based on data from 2 years (2008–2010 Skálafellsjökull north melt 14.2% (s.d = 0.8%), Skálafellsjökull north rainfall 5.2% (s.d. = 0.92%), Skálafellsjökull north lake melt 0.03% (s.d. = 0.001%), Heinabergsjökull melt 42.8% (s.d. = 2.3%), Heinabergsjökull rainfall 5.6% (s.d. = 0.5%), Heinabergsjökull lake melt 0.7% (s.d. = 0.1%), non-glacial catchment 31.1% (s.d. = 1.9%). This allowed us to isolate the part related to Skálafellsjökull north, which represented 19.4% (s.d. = 0.7%) of the Kolgríma river drainage. The mean error of input (melt and rainfall) is shown in Fig. 3.

We can also compare the discharge patterns of the Stađará and Kolgríma rivers. The winter base, winter peak defined as the 95% percentile, summer average and summer peak discharge defined as the 95% percentile, from the two rivers are very strongly related (r² = 0.96). This allows us to reproduce a discharge record for different parts of Skálafellsjökull from Kolgríma discharge; Sultartungnajökull catchment (5%, s.d. = 0.36%) and Skálafellsjökull as a whole (24%, s.d. = 2.7%).

The quantity and pattern of the two methods of measuring discharge, image processing and river gauge, were very similar. They both show a winter base discharge with distinct winter peaks. This gives confidence that the quantitative results achieved by the time-lapse camera are sufficiently robust.

Discharge modelling

We constructed an empirical model for discharge over a drainage cycle during winter at the field site. Using the 2012/2013 data, each cycle is divided into four phases (Fig. 4 and Table 1). Since it can be seen that cycle 1 (DOY 298–315) and cycle 7 (DOY 43–61) in 2012/13 are different from the others (discussed in more detail below), the mean and standard deviation values for the winter have been calculated for cycles 2–6. There is a strong correlation between positive degree days and rainfall, with rain present on all the high melt days, although there is no relationship between the amount of rainfall and melt.

During the first phase (I) there is low melt, and so the second phase (II) begins on the day when the daily melt M_k first exceeds a threshold M_t, set to 1.7 × 10⁴ m³, except for cycle 2 when the threshold is 1.4 × 10⁴ m³.

During the first stage of the first cycle, prior to the melt exceeding M_t, we assume a linear increase in discharge from a base rate:

$${Q}_{j}^{\left({{{{{\rm{c}}}}}}\right)}={Q}_{0}+jI$$

(2)

where ${Q}_{j}^{({{{{{\rm{c}}}}}})}$ is the discharge for day j of cycle c. Q₀ is a constant set equal to the observed daily discharge at the start of cycle 1, equal to 4.28 × 10⁴ m³, and I is the daily increment equal to 2.5 × 10³ m³. This reflects the mean melt during Phase I. In subsequent cycles, the daily discharge during the first stage is set to a constant 1.15 × 10⁴ m³ (based on the mean discharge during Phase I) plus rainfall (if present).

The second stage begins on day k of the cycle and ends on day e. During this phase the daily discharge is set equal to the previous day’s discharge plus the melt (M) and rainfall (R) for the day. There was a maximum rainfall value of 4 × 10⁴ m³, reflecting the maximum capacity of the system, for the first day of high rainfall, which was doubled on the following day. The remainder was carried over to the subsequent days. In addition, on day k the total melt since the start of the cycle is discharged. On the day before the end of the cycle a storage element equal to 2.5 × 10³ m³ multiplied by the number of days since the start of the cycle is added, and on the final day of the cycle the discharge is set to 1.7 × 10⁴ m³ (based on the minimum discharge during Phase IV). This can be written as:

$${Q}_{k}^{\left({{{{{\rm{c}}}}}}\right)} ={Q}_{{{k}}-1}^{\left({{{{{\rm{c}}}}}}\right)}+\mathop{\sum }\limits_{{{i}}=1}^{{{k}}}{M}_{{{i}}}+{R}_{i}\\ {Q}_{{{j}}}^{\left({{{{{\rm{c}}}}}}\right)} ={Q}_{{{j}}-1}^{\left({{{{{\rm{c}}}}}}\right)}+{M}_{{{j}}}+{R}_{i}\,,{{j}}={{k}}+1\ldots {{e}}-2 \\ {Q}_{{{e}}-1}^{\left({{{{{\rm{c}}}}}}\right)} ={Q}_{{{j}}-1}^{\left({{{{{\rm{c}}}}}}\right)}+{M}_{{{j}}}+{R}_{i}+2.5\times {10}^{3}\left({{e}}-3\right) \\ {Q}_{{{e}}}^{\left({{{{{\rm{c}}}}}}\right)} =1.7\times {10}^{4}$$

(3)