Introduction

The kagome lattices have drawn great attention in the community due to their inherent geometrical spin frustration1. They provide good platforms for exploring many exotic electronic states such as quantum spin liquid2,3,4 and other intriguing charge or magnetic orders5,6. Subsequently, more focus has been directed towards the electronic band structure of the kagome lattices, which is expected to possess saddle points, topological Dirac cones, and flat bands7,8. Consequently, superconductors with kagome lattices may have potential unconventional pairing mechanisms9. Notably, the Laves phases, as a well-known family of intermetallic compounds with kagome lattices, have diverse crystal structures such as the cubic C15-type (MgCu2) and the hexagonal C14-type (MgZn2)10,11. Several C15-type Laves phase superconductors, such as CeRu2 and ZrV212,13, have been reported as possible unconventional superconductors. Recently, due to the strong spin-orbit coupling (SOC) of Ir, researchers have focused on the Iridium-based C15 Laves phases AIr2 (A = Ca, Sr, Ba, Th, Sc, Zr)14,15,16,17,18. Many reports suggest the possibility of anomalous electronic states and possible unconventional superconductivity19,20,21. Among them, the Tc of ScIr2 was reported to be 2 ~ 2.4 K a long time ago22. Early calculations of the band structures for ScIr2 have confirmed that the density of states (DOS) near the Fermi level is mainly contributed by the 5d electrons of Ir, and the band structure is highly influenced by the strong SOC effect23,24.

Some special energy bands without or with weak dispersions are called flat bands, which themselves have fascinating properties, such as the correlated insulating states and unconventional superconductivity25. The flat bands have a large effective mass and relatively small kinetic energy of electrons. As a result, many-body effects dominate, leading to the strong correlation effects and non-Fermi-liquid behavior26. Flat bands are often observed in kagome materials, such as unconventional superconductors AV3Sb5 and ATi3Bi5 (A = K, Rb, and Cs)27,28. In addition, when considering SOC, the electronic bands tend to split, which sometimes also produces flat bands29. Many theoretical and experimental studies were initiated on the relationship between flat bands and superconductivity30,31. For kagome superconductor LaRu3Si5, the presence of flat bands brings about the high DOS at the Fermi energy, which enhances its Tc32. In addition to enhanced superconducting pairing, flat bands also lead to strong superconducting fluctuations (SCFs)33. In addition, exotic quantum phenomena are often observed in materials with flat bands due to the induced strong correlation effect. For the well-known twist graphene with magic angles, the flat band at half-filling leads to the correlated insulating states34. For kagome metal Ni3In, the strong electron-electron interactions induced by their flat bands lead to the upturn of the specific heat coefficient observed at low temperatures35. Superconductors with electronic flat bands deserve more in-depth studies, including their exotic physical properties and the potential unconventional superconductivity.

In this study, a nonmonotonic and two-dome-like doping dependence of Tc was observed for a series of Sc2Ir4-xSix (x = 0 ~ 0.7). For some samples in the second dome region, we observed non-Fermi-liquid behavior at low temperatures in their normal states. The normal state resistivity increases as the temperature decreases. The normal-state specific heat coefficient deviates from the Debye model and shows a divergence at low temperatures. At the optimal doping point, the superconductivity is enhanced, showing pronounced SCFs. All these can be attributed to the strong correlation effect, which is mainly induced by the tunable flat band near the Fermi surface, relevant to the kagome structure and the SOC effect.

Results

Crystal structure and their superconducting characterization

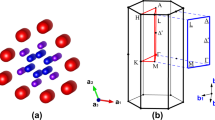
For the crystal structure of ScIr2, the basic lattice is pyrochlore, and interestingly its 2D projection is the kagome lattice. Here, Ir atoms form kagome lattices in the planes perpendicular to the [111] direction shown in Fig. 1a. We synthesized a series of polycrystalline samples of Sc2Ir4-xSix (x = 0 ~ 0.7) by the arc melting method. Similar to several other ternary C15-type Laves phases reported previously (e.g., Mg2Ni3.2Ge0.8, Mn2Ni3Ge, Nd2Ni3.5Si0.5 and Mg2Ni3As)36,37,38, Ir atoms are partially substituted by nonmetallic Si atoms, which are randomly distributed in the kagome lattice. The high quality and bulk superconductivity of all samples were confirmed by the Powder X-ray diffraction (see Supplementary Fig. 1) and magnetic susceptibility measurements (see Supplementary Fig. 2). The resistances of all samples are shown in Fig. 1b, one can see that the variation of Tc is nonmonotonic with increasing doping level of Si. At a low doping level x = 0.1, the Tc decreases. Unexpectedly, as the doping level increases, the Tc starts to rise. The highest Tc is then observed as the doping around x = 0.5. There is an upper limit of Si doping for this system (see Supplementary Fig. 1), with another decrease in Tc for x = 0.7. The origin of nonmonotonic Tc dependence is puzzling and attractive. We further investigated the transport properties and surprisingly observed the unusual normal state.

Fig. 1: The crystal structure and the temperature dependence of resistivity measured in Sc2Ir4-xSix.
figure 1

a The kagome lattice of Ir for ScIr2 viewed from the planes perpendicular to the [111] direction. It belongs to the C15 type laves phase with a space group of Fd − 3 m (see Supplementary Fig. 1a). For the pristine, every four Ir atoms form a tetrahedron which is connected through sharing vertices. In one unit cell, four small tetrahedra of Ir occupy the vertex positions of a larger tetrahedron. b The normalized resistance of Sc2Ir4-xSix (x = 0.0 ~ 0.7) from 2 K to 300 K. The inset shows the enlarged view of the superconducting transitions around Tc.

Full size image

Specific heat in the normal and superconducting states

Figure 2a and b show the low-temperature specific heat of Sc2Ir3.7Si0.3 and Sc2Ir3.5Si0.5. When the magnetic field completely suppresses superconductivity (see Supplementary Fig. 3), the specific heat coefficient increases slightly (about 8% increase from the minimum) at very low temperatures for Sc2Ir3.7Si0.3. For Sc2Ir3.5Si0.5 with higher Tc, the increasing trend is more pronounced (up to about 20% increase from the minimum) at low temperatures, clearly indicating the divergence of the specific heat coefficient. Such upturns emerge only after superconductivity is completely suppressed by the magnetic field. We can rule out the possibility of the Schottky anomaly in specific heat39. If it is the case, the divergence (as part of the peak of Schottky anomaly) at zero and low fields, should gradually become broadened and finally smear out at higher fields40,41. However, the data at 6 and 9 T overlap nicely. Therefore, the observed upturn of the specific heat coefficient at low temperatures should be the intrinsic property of the normal state. As shown in the insets of Figs. 2(a) and 2(b), the specific heat coefficient C/T at low temperatures is well-fitted by the linear relationship with -lnT. Concerning the upturn of C/T, there are various understandings. On one hand, some strange metals near the quantum critical points (QCP) with strong quantum fluctuations show the logarithmic temperature dependence as Ce/T = A ln(T0/T) in the low-temperature limit, and are often accompanied by the linear T dependent resistivity42,43,44,45. On the other hand, for example, for the heavy fermion superconductors, the upturn of specific heat coefficient at low temperatures is often attributed to the enormous enhancement of the effective mass of the quasiparticles, due to the strong correlation effect46. Although the upturn of the specific heat coefficient at low temperatures here is indeed a signature of an unconventional ground state, further analysis is necessary to distinguish its origin.

Fig. 2: The temperature dependence of specific heat measured under different magnetic fields for Sc2Ir3.7Si0.3 and Sc2Ir3.5Si0.5.
figure 2

Temperature dependence of specific heat under different magnetic fields below 6 K for a Sc2Ir3.7Si0.3, b, Sc2Ir3.5Si0.5. Sharp superconducting transitions can be seen here at 0 T. And when applying magnetic fields, the superconducting transition shifts to lower temperatures and smears out. At 6 T and 9T, they entered the unconventional ground state with an increasing trend below 1 K. Insets show the enlarged view of C/T versus lnT. It can be fitted well with the linear relationship below 1 K.

Full size image

Usually, the normal-state specific heat at low temperatures (<10 K) obeys the Debye model with C/T = γ + βT2 for a Fermi liquid ground state, showing a linear relation in C/T versus T2. However, we find that the specific heat coefficient deviates from the linear relationship with T2 below 6 K, and the fitting to the normal-state specific heat of Sc2Ir3.5Si0.5 by the Debye model yields a negative intercept of the specific heat coefficient in the zero-temperature limit, as shown by the purple line in Fig. 3a. The Sommerfeld constant γn, which implies the effective DOS near the Fermi energy, must be positive. Considering the correlation effect, in the fitting process, we introduce an additional contribution -ATnln(T - δ) which arises from the enhanced electron-electron interactions47. The Debye model together with strong correlations shown as the blue line can fit the experimental data very well down to 0.5 K. The fitting parameter n ≈ 2.2 < 3 again confirms the strong correlations in this system. It is the direct experimental evidence for strong correlation effects from specific heat data47. The above analysis can successfully attribute the low-temperature upturn of the specific heat coefficient to a strong correlation effect.

Fig. 3: The unconventional normal-state and superconducting-state specific heat data for Sc2Ir3.5Si0.5.
figure 3

a The specific heat coefficient C/T versus T2 at 0 T and 6 T. The normal state data (as the green symbols) deviates from the usual Debye model (as the purple line) but can be well fitted when additionally considering the electron correlations (as the blue line). The inset is an enlarged view of the fits at low temperatures. b The electronic specific heat coefficient at 0 T and the fitting curves with three different gap structures.

Full size image

We use the experimental data of specific heat at 6 T as the normal-state value and subtract it from the data at 0 T to obtain the electronic specific heat coefficient, and the result is shown in Fig. 3b. The rounded shape of ΔCel/T near Tc is due to a slight inhomogeneous distribution of Tc within the sample48. Then we use the BCS formula with three different gap structures to fit it (see Supplementary Note 1). Down to 0.5 K, the electronic specific heat coefficient decreases continuously without any trend of flattening. The fully gapped isotropic s-wave model plotted as the red line can be safely ruled out. The difference between extended s-wave and d-wave lies in the presence of energy gap nodes. It is not yet possible to directly determine the trend of electronic-specific heat at very low temperatures. Thus, we cannot directly distinguish between the fits of the two gap structures indicated by the blue and green lines. However, the specific heat coefficient at 9 T for the normal state in Fig. 2b shows a slight increase at low temperatures (<1 K). And the specific heat coefficient at 0 T for the superconducting state, shows a tendency to flatten out slowly at low temperatures. Subtracting the normal-state data from the zero-field data suggests that the electronic specific heat coefficient of the superconducting state (γ - γn) will continue to decrease towards lower temperatures (<0.4 K). This violates the expectation for an s-wave pairing but is consistent with a d-wave pairing. Thus, it indicates a preference of d-wave pairing with gap nodes. As shown in the inset of Fig. 3a, the residual specific heat coefficient γ0 at zero field is very small for our polycrystalline sample, indicating its high purity. However, it may also suggest inconsistency with d-wave superconductivity, which typically exhibits a finite residual γ0 at zero field due to nodal quasiparticles for single crystals with some disorders. In the case of anisotropic s-wave superconductivity with gap minima, the residual γ0 at zero field may be close to zero without excited quasiparticles. From this perspective, the pairing symmetry for the sample with x = 0.5 suggests the possibility of an extended s-wave. The magnetic field-induced specific heat coefficient at low temperatures (see Supplementary Fig. 4) exhibits a power law relationship of H1/2. This relationship can be satisfied by both d-wave and highly anisotropic s-wave superconductors. Therefore, the pairing symmetry of the gap for the sample with x = 0.5 is interesting but remains to be determined.

Resistivity in the normal and superconducting states

As shown in Fig. 4a and b, the electric transport properties also show the anomalous ground state. For Sc2Ir3.7Si0.3, the resistivity increases slightly below 12 K at 6 and 9 T, behaving like a semiconductor. With careful resistivity measurements, the magnetoresistance for both samples is too small and can be neglected. The semiconducting behavior is more pronounced for Sc2Ir3.5Si0.5. The upturn of resistivity at low temperatures observed here differs from the linear resistivity feature around QCP42,43,44,45. Both samples behave as the Fermi liquid above Tc at 0 T, with a large residual resistivity (see Supplementary Fig. 5). Before further analyzing the unusual normal state, we should exclude other factors and confirm that this is indeed an intrinsic property. First, this is diametrically opposed to the well-known Kondo effect49, for which, the resistivity increases below the Kondo temperature at 0 T due to the localized magnetic moments of the impurities, and eventually behaves as the Fermi liquid when the magnetic field is sufficiently high50. Second, the normal state resistivity at 6 T overlaps well with the data at 9 T. If the increase of the low-temperature resistivity would be caused by the positive magneto-resistance (MR) at low temperatures, it should be larger at 9 T than at 6 T, which is opposite to our observations. Third, it is possible to exclude the weak Anderson localization as the origin for the upturn of resistivity at low temperatures51,52. For Anderson localization, it should exist at zero field, and a delocalization effect may occur when a magnetic field is applied. But the data in Fig. 4 show the opposite behavior. Furthermore, if we attribute the low-temperature upturn of resistivity to Anderson localization which is induced by the doped impurities and disorders in the sample, we would expect a larger scattering and stronger enhancement of low-temperature resistivity with a higher concentration of Si doping, but the experimental data do not support that. The upturn of resistivity is less pronounced at x = 0.7, which is expected to have a higher concentration of impurities compared to x = 0.5 doping.

Fig. 4: The unconventional normal-state and superconducting-state for two samples evidenced by resistivity.
figure 4

Temperature dependence of resistivity under various magnetic fields from 2 K to 50 K for Sc2Ir3.7Si0.3 (a) and Sc2Ir3.5Si0.5 (b). The solid dots with different colors represent the actual measured data, and the solid lines represent the corresponding curves after smoothed. The temperatures corresponding to the minimum resistance values are denoted as Tmin. The onset points of the superconducting transition of resistivity are marked as Tc*.

Full size image

When combined with the specific heat data, it is interesting to note that the upturn of low-temperature resistivity and the upturn of the low-temperature specific heat coefficient occur almost concurrently for some doping levels, as shown in Fig. 2, Fig. 4 and Supplementary Fig. 6. This strongly suggests that they may share the same origin. The upturn of the low-temperature specific heat coefficient can be well explained by the strong correlation effect in the system rather than the Anderson localization. Thus, we can exclude the Anderson localization, and instead attribute the upturn of resistivity at low temperatures to the strong electronic correlation effect. The carrier concentration at low temperatures in this sample is quite large and appears to be almost independent of temperature (see Supplementary Fig. 3c). The relationship between Hall coefficient (RH) and resistivity (ρ) determines mobility (μH), expressed as μH = RH/ρ. Here, below 20 K, with the decreasing temperature, the Hall coefficient remains nearly constant, while the resistivity increases. Thus, the decrease in mobility at low temperatures is most likely related to the enhancement of the electron effective mass. In contrast to materials with Landau-Fermi liquid behavior, where electrons are free to move, strongly correlated materials have electrons with gradually enhanced effective mass, leading to the appearance of localization effect. This results in a decrease of electron mobility and exhibits as a semiconducting behavior in the normal state. As in heavy fermion systems, the enhanced effective mass makes it difficult for electrons to move freely, resulting in weak insulation in their ground states53,54. In many cases, it may lead to strong correlation effects and potentially induce unconventional insulating normal states. For example, flat bands may be one of the factors55,56. Therefore, the ground state of the samples with increased resistivity at low temperatures may also indicate a strong correlation effect in the present system.

Additionally, strong SCFs were observed for the samples around the optimal doping point. As can be seen in Fig. 4(b), the superconducting transition of resistivity at the onset point is very round, and we define the critical temperature Tc* ≈ 5.7 K at which the resistivity starts to drop. The decrease of resistivity from Tc* to Tc is significantly larger compared to the nearly constant resistivity over a wide temperature range above Tc*. Broadened superconducting transitions are observed in the temperature-dependent resistivity due to superconducting fluctuations, particularly near the onset transition temperature57. Therefore, we consider this to be a sign of SCFs. The enhanced conductivity extends up to Tc* (≈ 2Tc) for Sc2Ir3.5Si0.5, showing pronounced SCFs, being similar to previous reports on other unconventional superconductors58. More strikingly, for Sc2Ir3.5Si0.5, if the resistivity at 6 T is considered as the normal-state resistivity, the resistivity at 0 T starts to deviate from the “normal state” at 18 K. This deviation point coincides with the temperature of the minimum resistivity. We may regard this point as the pseudogap temperature, which probably corresponds to the preformed Cooper pairs but without long-range phase coherence. This needs however more experimental verifications. Despite the large temperature region for the SCFs, the specific heat jump and the demagnetization transition near Tc are quite sharp with seemingly no trace of SCFs, this may be interpreted as the resolution limit on the tiny entropy contribution by the partial Cooper pairs in the SCF region.

Discussions

In the phase diagram shown in Fig. 5a, we summarized Tc and residual resistance ratio (RRR = R300 K/R5 K), which reveals two superconducting domes. Interestingly, the doping dependence of Tc is opposite to the RRR. The fact that the values of RRR in highly doped samples are close to 1 suggests the disordered distribution of Si atoms in the lattice, which is similar to the high-entropy alloys and other doped metals59. In this system, the calculated mean free path is a little smaller than the calculated coherence length which again confirms the disordered state (see Supplementary Fig. 3). However, despite the disordering in the sample, we believe there is still a possibility to have a superconducting gap with high anisotropy. The superconducting material can be described as a disordered network of Josephson junctions. Here, the normal state resistivity is still not very big and the charge carrier density is quite high, thus the Josephson coupling between grains should be very strong. This argument is strengthened when the coherence length is long. Additionally, the presence of a strong correlation effect reduces the influence of disorders on superconductivity60. In general, the doping of Si atoms may introduce more impurity scattering and destroy the superconductivity61. However, the RRR increases for samples with x = 0.1, compared to the pristine sample. A larger RRR indicates better metallic behavior and less residual electron scattering caused by disorders. Therefore, the decrease in Tc may be due to intrinsic physical properties rather than impurity scattering or lattice distortion. Then, the Tc value increases again with further doping Si for the sample with x = 0.3, while the RRR decreases and approaches to 1. Such an opposing relationship between the evolution of RRR and Tc, further indicates that the increase of Tc is the unique and intrinsic property of the series samples. The highest Tc is then observed at the doping level around x = 0.5 with the lowest RRR about 1.04. The presence of nonmonotonic doping or pressure-dependent Tc in the phase diagram in many systems is quite often accompanied by the occurrence of unconventional superconductivity, such as in cuprates, iron-based superconductors, and recently discovered CsV3Sb562,63,64,65,66. In the phase diagram of Fig. 5a, we also list the Tc* from their resistivity measurements. Notably, just like the evolution of Tc, the doping dependence of Tc* shows a more pronounced enhancement around optimal doping. Thus, the enhancement of Tc* is closely related to the origin of the two superconducting domes. However, the reason for the unusual phase diagram is still missing.

Fig. 5: The evolution of their unconventional superconductivity with Si doping level.
figure 5

a The phase diagram of Sc2Ir4−xSix involving Tc (measured by resistivity and specific heat), Tc* and RRR. b Doping dependence of the electronic specific heat coefficient γn in the normal state, the degree of the increase of resistivity measured by [R2 K−Rmin]/Rmin, and the divergence of specific heat coefficient measured by [γ0.45 K−γmin]/γmin for these samples. Here, both γmin and Rmin are the associated values at the minimum points of resistivity and specific heat coefficient in the normal state, respectively.

Full size image

Interestingly, both the resistivity and specific heat exhibit non-Fermi-liquid behavior at low temperatures in their normal states. These have been explained as signatures of strong correlation effects in the system. Moreover, neither signature of semiconducting behaviors nor divergence of the specific heat coefficient has been observed for the pristine and slightly doped Sc2Ir3.9Si0.1 sample at low temperatures in their normal states (see Supplementary Fig. 6). However, it is found that the anomalous normal-state behavior also exists for Sc2Ir3.3Si0.7, but not as pronounced as that for Sc2Ir3.5Si0.5. The increase of the specific heat coefficient as (γ0.45 K - γmin)/γmin and the increase of the resistance as (R2 K - Rmin)/ Rmin are shown in Fig. 5b. These are also in good agreement with the evolutions of Tc for the samples and only exist in the second superconducting dome, where Tc is again increased. Therefore, we can conclude that the strange non-Fermi-liquid behavior which is attributed to the strong correlation effect, is strongly related to the enhancement of Tc in the second superconducting dome. We believe they should have the same origin.

Furthermore, the estimated γn is also consistent with the doping-dependent Tc. The γn represents the DOS in the normal state near the Fermi energy. For Sc2Ir4 and Sc2Ir3.9Si0.1, we get γn by a linear extension of the normal-state specific heat coefficient to 0 K. And for other samples with the low-temperature divergence, we obtain γn by fitting the data to the logarithmic relation. Figure 5b shows the evolution of γn with doping. Considering the unphysical infinitely large value of γn given by that logarithmic equation, we choose the γn at 0.01 K. It shows a strong increase in the second superconducting dome, especially at the optimal doping point with the highest Tc. Thus, the strongly enhanced DOS is responsible for the nonmonotonic doping dependent Tc, which is closely related to the anomalous normal state in the second superconducting dome. Moreover, the enhancement of effective DOS is closely related to the occurrence of the SCFs evidenced by the evolution of Tc*. Therefore, the logarithmic increase of specific heat coefficient at low temperatures indicates the divergence of the DOS. And the divergence of the DOS is often accompanied by an increase in the electronic effective mass, which is related to the enhancement of the electronic correlation and quantum fluctuations. The increase in effective mass with decreasing temperature is often associated with the existence of QCP. However, both the broad doping range for the existence of non-Fermi liquid behavior and the absence of the linear resistivity feature make us hesitant to attribute it to the quantum criticality. To explain the enhanced DOS in the second superconducting dome, we conducted the theoretical calculations of the electronic band structures, which is shown in Fig. 6.

Fig. 6: Calculated electronic band structures around the Fermi energy (EF).
figure 6

The total band structure without and with SOC for a Sc2Ir4 and for b Sc2Ir3.5Si0.5. The black ellipses show the change of the electron pockets near the Fermi level. The purple frames represent a slightly flat band between Γ and L points. The green frames highlight the subsequent flat band near the Fermi energy. In the lower right corner is the enlarged view of the flat band. The panel on the right-hand side of (b) shows the partial and total DOS of Sc2Ir3.5Si0.5 with SOC.

Full size image

One can see that the dominant contribution to the DOS near Fermi energy EF comes from the 5d electrons of Ir which play an important role in superconductivity (see Supplementary Fig. 7). When the strong SOC of Ir is taken into account23,24, the large band splitting occurs, resulting in intriguing features. Initially, for the pristine sample in Fig. 6a, the two-electron pockets around Γ provide the main DOS, although it contains also a slightly flat band between Γ-L after considering the SOC effect. However, after a small amount of Si doping, for example, x = 0.1 or smaller, these two electron bands around Γ are shifted upwards, and also this slightly flat band is shifted far away from the Fermi level, leading to the decreased contribution of DOS at the Fermi energy. This explains the decrease of Tc in the first superconducting dome. Meanwhile, with further doping of Si atoms, up to x = 0.5, another flatter band finally appears along the Γ-L direction and is very close to the Fermi level (approximately 20 meV away below, see Supplementary Fig. 8). The electrons on the flat band near the Fermi energy (about 7.75 eV) play a very important role in the process of pair scattering. The electrons on the flat band have a large effective mass, resulting in the strong correlation effect and the strongly increased DOS in the second superconducting dome. The combination of two features in the energy band structure, namely, less contribution of DOS from the Fermi pockets near Γ and the shift of flat bands after Si doping, can qualitatively explain the gradually enhanced correlation effect and the nonmonotonic doping dependence of γn obtained from the specific heat measurements. In addition, correlations between electrons will gradually dominate due to the presence of the flat band, which also explains the deviation of the normal-state specific heat from the Debye model. To summarize, the shrinkage of the Fermi surface near Γ and the presence of a flat band may cooperatively lead to an enhanced correlation effect, resulting in the non-Fermi-liquid behavior in the normal state in the region of the second superconducting dome. The strong spin-orbit coupling induced flat band can well explain the increase in effective mass and the strong correlation effect. Thus, due to the lack of strong evidence supporting the existence of QCP, it remains uncertain whether the flat band induces other quantum phase transitions.

Conclusions

In conclusion, we have successfully synthesized a superconducting system Sc2Ir4-xSix with a phase diagram containing two superconducting domes. Many characteristics show that the superconducting state and normal state in the second dome are anomalous. This can be corroborated by the observations that (1) the normal states exhibit non-Fermi-liquid behaviors characterized by the logarithmic divergence of specific heat coefficient and the increased resistivity at low temperatures; (2) strong superconducting fluctuations occur far above Tc at the optimal doping; (3) our theoretical calculations indicate that a flat band induced by the strong splitting after SOC can give a natural understanding of the tunable correlation effect, which can enhance Tc and induce strong superconducting fluctuations. All of the above findings provide other insights into the relationship between the strong correlation effect and superconductivity in this interesting Iridium-based kagome system.

Methods

Sample growth

The polycrystalline samples of Sc2Ir4-xSix (x = 0 ~ 0.7) were synthesized by the arc-melting method. The raw materials scandium (99.9%, 22 mesh, Alfa Aesar), iridium (99.5%, 325 mesh, Alfa Aesar), and silicon (99.99%, 100 mesh, Alfa Aesar) were weighed in stoichiometric proportions, grounded and then pressed into a pellet in a glove box (water moisture and the oxygen compositions are below 0.1 PPM). To obtain a uniform sample, every pellet was melted at least three times and flipped over at intermediate intervals. The resulting air-stable pellets were wrapped with Ta sheets, sealed in an evacuated quartz tube under a high vacuum, and annealed at 800 °C for 4 days.

Sample characterizations

The crystal structure was evaluated via XRD (Bruker, D8 Advance diffractometer) with Cu Kα radiation (λ = 1.5418 Å). The intensity data were obtained over the 2θ range of 10° to 100°, with a step width of 0.01°. The Rietveld refinements were conducted with TOPAS 4.2 software67. The dc magnetization measurements were performed with a SQUID-VSM-7 T down to 1.8 K (Quantum Design). The electrical resistivity measurements were measured by employing a standard four-probe method with a physical property measurement system (PPMS 16 T, Quantum Design). Samples prepared for resistivity measurements and made of four electrodes should be handled with caution to avoid the influence of other measurement signals on the raw data. The specific heat was measured by the thermal-relaxation method with an additional 3He insert using the PPMS-16 T. To calculate the electronic band structure with and without the spin-orbit coupling, we performed the first-principles calculations using the Vienna Ab initio Simulation Package (VASP)68,69. The generalized gradient approximation (GGA) in the Perdew-Burke Ernzerhof form70 was used in the self-consistently calculation of the electronic structure. Here, we set a 9×9×9 k mesh with a cutoff energy of 370 eV, and the virtual-crystal approximation (VCA) was used to take into account the effect of partial substitution of Si for Ir.