Abstract
Emerging 4D printing techniques have enabled the realization of smart materials whose shape or properties can change with time. Two important phenomena play important roles in the 4D printing of shape memory polymeric materials. First, the anisotropic deformation of the printed filaments due to residual stresses can be harnessed to create out-of-plane shape transformations. Second, the unavoidable formation of micro-defects during the printing processes often affects the programmability of the printed object. Here, we propose a design approach that harnesses these two effects occurring during fused deposition modeling to create tailor-made curved geometries from initially 2D flat disks. We first determined the size and distribution of the imperfections formed within printed structures by varying two printing parameters namely the printing speed and the number of printed materials. Spatially varying the printing speed and combining polylactic acid filaments with a softer material without shape memory properties allowed us to cover a variety of shapes from negative to positive values of the mean and Gaussian curvature. We propose an analytical model to calculate the magnitude of the maximum out-of-plane deformation from the anisotropic expansion factor of the constituting microstructures. Furthermore, we develop computational models to predict the complex shape-changing of thermally actuated 4D printed structures given the distribution of rationally introduced imperfections and we demonstrate the potential applications of such defect-based metamaterials in drug delivery systems.
Similar content being viewed by others
Introduction
Shape-changing phenomena frequently occur in our everyday life: a flat leaf curls after falling from a tree due to drying, or a thin slice of fresh wood undergoes an irreversible shape transformation from a flat state into a dome-like shape due to a drying process1,2 (Fig. 1a). More often than not, however, shape-shifting in nature is a reversible dynamic process and follows differential growth morphogenesis patterns3,4. Examples are cuttlefish5, squids6, and Bauhinia pods7 whose complex biological microstructures enable them to adapt their body shape, stiffness, and behavior to create elaborate shape changes, once triggered by external stimuli. Mimicking natural shape-shifting principles8 has led to the emergence of a new class of engineered materials with tailor-made shape-morphing capabilities that have numerous applications in soft matter (e.g., soft actuators9 and soft robotics10), programmable materials (e.g., mechanical metamaterials11,12,13,14,15,16 and reconfigurable materials17,18), and medical devices (e.g., drug delivery vehicles19 and microfluidic systems20).
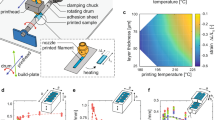
Shape-shifting frequently occurs in nature because of drying processes and material shrinkage. A freshly cut slice of wood, with its orthotropic mechanical properties62, transforms from a flat state into a dome-like shape upon drying1,2 (a). Similar out-of-plane shape transformations take place when a 4D printed disk made of shape memory polymers is exposed to high temperatures (b). Based on the empirical Eq. (2), the out-of-plane deformation of the disk and the resulting cone angle depend on the equivalent lateral and longitudinal expansion factors (\({\beta }_{1}\) and \({\beta }_{2}\)) (c). By changing the printing speed, one can adjust the equivalent longitudinal and transverse expansion factors and, thus, the deformation angle (\(\theta\)) (d). The angles calculated from the empirical Eq. (2) for different printing speeds were compared to experimental and numerical results (d). We 4D printed disks with various printing speeds, including a constant printing speed (e), a step-wise printing speed in which the inner part of the disk was printed at a speed of 20 mm s−1 while the outer part was printed at 80 mm s−1 (f), a gradually increasing the printing speed from 20 mm s−1 at the center to 80 at the peripheral edge of the disk (g), and a step-wise printing speed in which the inner part of the disk was printed with a speed of 80 mm s−1 while the outer was printed at 20 mm s−1 (h). The surfaces shown in (e–h) are the first deposited layers (F.D.L).
Successful spatiotemporal planning of an arbitrary shape-morphing behavior depends on two main factors. First, one needs to select the proper type of actuation (e.g., thermal, light, electromagnetic, swelling, or pH) and stimuli-responsive material (e.g., shape memory polymers21,22, magneto-rheological elastomers23,24, liquid crystal polymers25, or hydrogels26,27). Second, the microscale geometry of the involved materials should be rationally designed to achieve local deformations that collectively give rise to the desired global shape-shifting behavior21,28,29. Several approaches based on origami30,31 and kirigami32,33,34 as well as a number of theoretical models35,36) have been proposed in the past for the rational and predictable design of such shape-shifting behaviors.
The emergence of additive manufacturing in general and multi-material 3D printing, in particular, has provided unparalleled opportunities to fabricate 4D printed structures with complex shape morphing capabilities. Among different 3D printing technologies, fused deposition modeling (FDM) is one of the most widely available technologies that has been used for the fabrication of 4D printed structures37,38. Tuning the printing parameters, such as the bed temperature, nozzle temperature, printing speed, and printing patterns, is shown to be an easy yet effective way to control the final shape of the 4D printed structures. From a microstructural viewpoint, these different parameters have two impacts: influencing the residual stresses stored in the polymeric material and affecting the level of fusion and bonding between individual filament strands or between the consecutive layers making up the printed structure. Residual stress, which is in general undesired, is related to the elongation of polymeric molecules along the printing direction during their extrusion through the printer nozzle and is a result of the quick solidification of the filament in its elongated state. If the printed material is brought to a temperature close to its glass transition temperature (\({T}_{g}\)), polymeric molecules tend to relax by creep, leading to an in-plane contraction of the material in the direction of the filament. Because of this anisotropic deformation, initially flat structures can adopt a 3D doubly curved shape21,28,39,40. In mathematical terms, metric distortions induce a change of the Gaussian curvature. However, if this relaxation is not uniform across the thickness, the structure also tends to bend due to the classical Timoshenko bilayer effect41. In addition to residual stresses, printing parameters dictate the quality of the bonding between adjacent filament strands. Poor bonding between filaments or layers may create undesired local imperfections that modify the local mechanical properties and, thus, the direction of (local) deformations. These imperfections can, consequently, cause arbitrary shape transformations under external stimuli. However, little is known about the exact formation mechanisms of such local micro-scale imperfections and how their morphological features (e.g., size and distribution) can be linked to the printing parameters. Moreover, such printing imperfections have been primarily seen as undesired, leading to their potential as a design tool for shape transformation remaining unexploited. It is, therefore, unclear how such imperfections in addition to residual stresses can be harvested as a design tool to create complex yet fully predictable and controllable shape transformations. Here, we turn the tables around by proposing to see imperfections and residual stresses distribution not as a threat to the success of 4D printing but rather as a design tool.
To put this in the context of the available literature, several studies have established that different types of curvatures can be achieved by modifying the geometrical design of the 4D printed object (e.g., layer thickness), through the use of multi-layer materials, as well as by introducing specific rationally designed printing patterns42,43,44. Local curvature tuning can also be accomplished by using multiple types of materials and by incorporating multiple stimuli43,45. However, the currently existing techniques impose serious limitations regarding the specimen design, specimen dimensions, and printing patterns. As main contributions of the current study, we propose an approach based on the synergistic effect of micro-scale imperfections and stress relaxation for introducing programmed shape transformations into the fabrication of 4D printed materials. The rational introduction of micro-scale imperfections has the advantage that it does not impose too many constraints regarding the geometry, material/layer composition, and printing patterns of 4D printed objects. This further expands the space of achievable shape transformations and makes the approach applicable to a wider range of materials, microarchitectural designs, and overall geometries. We will demonstrate the utility of the proposed approach both in its own right and in combination with some of the already existing approaches. Toward that ambition, we elucidate the role of undesired microstructural imperfections occurring during the FDM printing process and propose a design strategy to exploit them, in combination with multi-material printing, to fully control and tailor the shape transformation of 4D printed parts. We will specifically focus on curved surfaces and will apply the developed methodology to transform flat plates into curved 3D surfaces with a wide range of positive and negative values of the mean and Gaussian curvatures.
Results and discussion
The role of residual stresses and micro-defects positioning
Polymeric filaments (in our case, polylactic acid (PLA)) generally exhibit residual stresses after the printing process. When the material is heated up to a temperature close to its glass transition temperature (typically 74 °C for PLA), residual stresses tend to relax, leading to longitudinal contraction and transverse expansion. The rest length and thickness of a filament with an initial length of \(l\) and an initial thickness of \(t\) are then given by: \({l}^{{\prime} }={\beta }_{1}l\) and \({t}^{{\prime} }={\beta }_{2}t\), where \({\beta }_{1}\) and \({\beta }_{2}\) are the longitudinal and transverse expansion factors, respectively (Fig. 1b). Both factors are expected to depend on the specific polymer properties and on the printing process, namely the printing speed (the higher the velocity, the higher the residual stress). Nevertheless, the proposed relaxation mechanism imposes \({\beta }_{1}\) < 1 and \({\beta }_{2}\) > 1 at the scale of an individual filament. Note that this effect differs from thermal expansion as the structures are eventually cooled down to their initial room temperature. Nevertheless, these transformations may be numerically treated as standard thermal expansion with anisotropic heat expansion coefficients.
Let us consider a flat disk 3D printed as a succession of concentric rings (in practice the printing path follows a single concentric ring). When heated up (\(\triangle T={{{{{\rm{cte}}}}}}\)), the disk will undergo anisotropic strains leading to out-of-plane deformations. In such an axisymmetric configuration, the expansion factors \({\beta }_{1}\) and \({\beta }_{2}\) may depend on the radial coordinate \(r\) in the reference flat disk. In the absence of any geometrical incompatibility and if the bending stiffness can be neglected, an initially flat annulus of inner radius \(r\) and width \(dr\) in the flat transforms into a tilted annulus of inner radius \(\rho ={\beta }_{1}(r)r\), an outer radius of \(\rho +d\rho ={\beta }_{1}(r+{dr}).(r+{dr})={\beta }_{1}(r)r+({\beta }_{1}(r)+r\frac{\partial {\beta }_{1}}{\partial r}){dr}\) and a width of \({\beta }_{2}(r){{{{{\rm{d}}}}}}r\) (Fig. 1b).
Therefore, the tilt angle of the annulus is given by:
If the expansion factors are uniform, the expected shape is a cone with a characteristic angle:
To probe this relation, several disks of thicknesses \(h\) = 2 mm were printed from PLA with different speeds ranging between 20 mm s−1 and 80 mm s−1 (the printing speed was uniform for each specimen). Once the heat stimulus is applied, the disks deform into cones with the most acute one corresponding to the highest printing speed, in qualitative agreement with Eq. (2) (Fig. 1 c-d). We measured the longitudinal expansion coefficients of the specimens printed at different printing speeds (Fig. 1c). Our experimental results confirmed that increasing the printing speed decreased the magnitude of the longitudinal expansion factor of the specimens (Fig. 1c). This can be explained by the fact that increasing the printing speed results in elongated filaments with smaller diameters. Interestingly, the effective values measured for \({\beta }_{2}\) are not larger than 1 as expected at the scale of a filament. We interpret this observation by the presence of void defects between the deposited filaments as described later. We also found an excellent agreement between the experimentally determined cone angles and the cone angles predicted analytically using Eq. (2) (Fig. 1d, e).
These results show that the printing speed can be considered as a design parameter to control the overall deformation of the printed disks. To obtain more complex shapes, we decomposed the disks into two regions (i.e., inner disk and outer annulus) (Fig. 1f), which were printed with the constant printing speeds of 20 and 80 mm s−1, respectively (Fig. 1f). We fixed the radius of the inner (\({R}_{{in}}\)) and outer (\(R\)) disks at four levels: \({R}_{{in}}/R=\) 90%, 80%, 70%, and 60%. In theory, abruptly changing the printing speed should induce a geometrical discontinuity in the local radius of the structure. Such discontinuities are, however, smoothed out by the material and the observed slope is close to the one predicted by Eq. (2).
To achieve a smoother deformation curve, we gradually increased the printing speed from the center to the periphery of the specimens using stepwise and linear functions (Fig. 1g). The stepwise functions were defined such that either three equal regions were printed at 20, 50, and 80 mm s−1 or four equal regions were printed at 20, 40, 60, and 80 mm s−1. When the printing speed was linearly increased, we obtained the smoothest shape-transformed curvature (Fig. 1g).
Furthermore, we 3D printed and tested square plates that were respectively printed at two distinct printing speeds: the minimum (i.e., 20 mm s−1) and the maximum (i.e., 80 mm s−1). The plate printed at the lower printing speed exhibited longitudinal shrinkage along the printing direction and transverse expansion (Supplementary Fig. S1a). Importantly, in this case, no out-of-plane deformation was observed in the overall deformation. Indeed, since the direction of contraction remains parallel and the contraction rate is uniform, Gaussian curvature is not expected to occur25. In contrast, the plate printed at the higher printing speed exhibited an unexpected out-of-plane deformation, appearing as a bending feature (Supplementary Fig. S1a). This observation highlighted that plates printed at a higher speed experience not only an in-plane stress but also a stress gradient through the plate thickness. The interplay between these two stress components contributes to different behavior when subjected to elevated temperatures. As a matter of fact, the layers printed at the vicinity of printer build-plate apparently accumulates less residual stress than the upper layers. As a consequence, standard bilayer effect tends to induce a concavity on the opposite side of the build-plate to the different structures that were printed with a uniform speed across the thickness41. Although this bending effect is not significant in the thicker specimens (beyond selecting the side where the concavity appears), bending is observed for thinner specimens (Supplementary Fig. S2).
To further confirm the role of the printing speed on the final shape of the disks, we inverted the printing speed of the inner and outer disks (i.e., the inner disk was printed at a speed of 80 mm s−1 while the outer section was printed at 20 mm s−1) (Fig. 1h). The deformation angles were nearly constant for the disks with the equal inner to outer ratios (i.e., \({R}_{{in}}/R=\) 60% and 70%) and were close to those calculated using Eq. 2 (Fig. 1h). However, for \({R}_{{in}}/R=\) 90%, the inner disk dominated the final deformation, resulting in a more complex shape. For this ratio, the proposed analytical equation is not anymore valid.
To put this relationship into a broader perspective, we printed PLA disks with various thicknesses. For very thin disks (i.e., \({{{{{\rm{h}}}}}}\) < 2 mm), the contribution of cross-sectional stresses caused the specimens to fold or roll when triggered by external thermal energy (Fig. 2a, and Supplementary Fig. S2). The overall bending deformation of the plates was optimum for a thickness of \({{{{{\rm{h}}}}}}\) = 2 mm, which is considered as the reference plate thickness throughout this study. For the specimens with larger thicknesses (i.e., \({{{{{\rm{h}}}}}}\) = 4 mm), the increase in the bending stiffness of the plates prevented them from fully bending (Fig. 2a, and Supplementary Fig. S2). The expansion factors (\({{{{{\beta }}}}}_{1},{{{{{\beta }}}}}_{2}\)) of the disks were not constant among disks with different thicknesses, although these variations decreased with the out-of-plane thickness of the specimens (Fig. 2b). These results were surprising, because we had not changed the printing parameters of the disks with different thicknesses. This can be attributed to changes in various factors, such as the change in the bending stiffness and the distribution of defects during the 3D printing process when changing the thickness of the disk. Furthermore, we 3D printed square-shaped specimens at speeds of 20 and 80 mm s−1. The results showed that \({{{{{\beta }}}}}_{2}\approx 1\) in the transverse direction, independent of the printing speed (Supplementary Fig. S1a). To explain this behavior, we further analyzed the mechanical properties of the constituent PLA as well as the morphological features of the 4D printed disks.
PLA disks of varying thicknesses behave differently when exposed to an external thermal stimulus (a). Disks with h \(=\) 2 mm thickness are considered as the reference specimens in this study because in-plane stresses dominate the shape-shifting behavior in thinner disks (i.e., \(h\) < 2 mm), causing the disk to fold or roll. When the sheet thicknesses are large enough (i.e., h ≥ 4 mm), the increased bending stiffness prevents the disks from fully bending (a). The experimentally measured expansion factors (\({\beta }_{1},{\beta }_{2}\)) were used in our computational models (b). The results of dynamic mechanical tests (i.e., storage moduli in a logarithmic scale (c–top), and \(\tan \delta\) (c–bottom)) performed on the PLA specimens printed with the maximum (i.e., 80 mm s−1) and minimum (i.e., 20 mm s−1) printing speeds and for the TPU specimens printed with a speed of 25 mm s−1. Constructed μCT images of a PLA disk were used to analyze the formation of micro-voids during the 4D printing process (d). A μCT image of a disk whose inner and outer parts were printed at 80 mm s−1 and 20 mm s−1, respectively. A morphological analysis of these specimens showed virtually no porosity for the PLA disks printed with the lowest speed (i.e., 20 mm s−1) and TPU while the level of porosity was significantly higher for the disks printed at 80 mm s−1 (e). The level of porosity also increased in the radial direction for the PLA disks printed at 80 mm s−1 (f). See Supplementary Movie 1 for the visualization of the defect distribution in the specimens printed at different speeds. The lines in subfigures e and f are to guide the eyes of readers.
We calculated the dynamic mechanical properties of the PLA cuboid bar-like specimens printed at two extreme printing speeds (i.e., 20 and 80 mm s−1) in the longitudinal direction (Fig. 2c). The storage and loss moduli of the PLA printed using two different speeds showed a similar trend (Fig. 2c), with the materials printed at the highest printing speed (i.e., 80 mm s−1) exhibiting slightly higher storage moduli beyond the glass transition temperature (Fig. 2c–top). This observation suggests that changing the printing speed has only limited impact on the mechanical properties of the material along the longitudinal direction. The glass transition temperatures of the specimens printed at the highest printing speed were also slightly higher (Fig. 2c–bottom).
The microstructural properties of the specimens printed at the highest printing speed were, however, significantly different (Fig. 2d–f, Supplementary Movie 1). We used micro-computed tomography to nondestructively measure the level of porosity (\(\varphi\)) in the disks printed at different printing speeds. The PLA disks printed at the lowest printing speed (i.e., 20 mm s−1) were almost free of defects (Fig. 2e), showing near-perfect bonding between their filaments and layers during the printing process. Printing at the highest printing speed (i.e., 80 mm s−1), on the other hand, resulted in the formation of micro-defects not only across the thickness of the disk but also radially (Fig. 2d–f). The initial printing layers, which were closer to the printing bed, were almost free of defects, while the amount of porosity linearly increased until it reached an asymptote \(\varphi \approx\) 30% for the top printing layers (Fig. 2e, Supplementary Movie 1). Micro-voids had also formed in the material in the form of concentric rings. The void fraction was smallest at the center of the disks and increased along the disk radius (Fig. 2f, Supplementary Movie 1).
The behavior of the 4D printed specimens is influenced by the distribution of micro-defects within the specimens. As illustrated in Fig. 2a, the impact of non-uniform distribution of micro-defects across the thickness is more pronounced for thinner specimens (i.e., \(h \, < \, 2\) mm) with a lower bending stiffness. These specimens are more likely to exhibit folding or rolling behaviors. Additionally, fewer defects and non-uniformities occur in the initial layers during the printing process (Fig. 2e–f). These characteristics collectively result in greater radial expansion, yielding an expansion factor (\({\beta }_{2}\)) greater than 1 (Fig. 2b). However, when the specimen thickness reaches 2 mm, other factors such as in-plane stresses, bending stiffness, and printing-induced non-uniformities become more significant. This leads to reduced transverse expansion and a decrease in the \({\beta }_{2}\) value (Fig. 2b). The specimens then become less susceptible to bending while shrinkage in the radial printing direction (\({\beta }_{1}\)) becomes more dominant.
We developed non-linear finite element models to simulate the shape-shifting behavior of the PLA disks. We defined the thermo-mechanical properties of its constituting elements based on the expansion factors measured in the experiments (Figs. 1c and 2b) and the dynamic mechanical tests (Fig. 2c) performed on pure PLA. We also implemented the experimentally observed geometrical imperfections (i.e., the level of porosity and its distribution) in our computational models (Fig. 2d–f). The distribution of the imperfections and their sizes (Supplementary Figure S3) were compatible with what was observed using micro-computed tomography (Fig. 2d–f). The deformation angles predicted by our computational models for the disks printed using different printing speeds were close to the experimentally measured values (Fig. 1d), confirming the validity of the proposed numerical approach. This also shows that the final shape of the 4D printed PLA disks depends not only on the proper distribution of anisotropic thermo-mechanical properties but also on the specific distribution of geometrical imperfections within the numerical model (Supplementary Fig. S3). We used the developed computational model to predict the shape-shifting behavior of other designs.
To highlight the interplay between the mechanical properties and microstructural features of the PLA disks, we analyzed the local curvatures of heat-actuated specimens. The specimens were divided into two regions with the inner part printed at the lowest printing speed (i.e., 20 mm s−1) and the outer at the highest speed (i.e., 80 mm s−1). For such specimens, the overall transformed shape (i.e., dome-like geometries) remained constant (Fig. 3a–left), exhibiting an overall negative mean curvature (i.e., \(H\)) and a positive Gaussian curvature (i.e., \(K\)) (Fig. 3a–right) at any point of the deformed disk. The discontinuity of the printing speed at the interface of two regions created a discontinuous deformation field at those regions, resulting in a local increase of the Gaussian curvature (Fig. 3a–left). Moreover, decreasing the size of the inner region decreased the deformation of the inner part, meaning that the maximum absolute values of the mean and Gaussian curvatures increased with the size of the outer disk (Fig. 3a–right). This can be explained by the presence of the additional voids distributed at the boundaries of the specimens as they were printed using the highest speed. The additional voids are created because the deposited filaments have less time to coalesce as the printing speed increases. The deformation is, therefore, more localized due to the existence of a higher density of initial voids in such structures.
The PLA disks were divided into two regions of which the inner part was printed at the minimum printing speed (i.e., 20 mm s−1) while the outer was printed with the maximum speed (i.e., 80 mm s−1). Four different ratios were used (i.e., \({R}_{{in}}/R\) = 60%, 70%, 80%, and 90%). Such a segmentation of the disks resulted in a discontinuous out-of-plane deformation of the specimens (a–left) and the development of a positive Gaussian curvature (i.e., \(K \, > \, 0\)) and a negative mean curvature (i.e., \(H \, < \, 0\)) (a–right). We then switched the printing speed of the inner (80 mm s−1) and outer (20 mm s−1) parts of the disk. This change resulted in a completely different shape transformations (b–left) and local curvatures (b–right). The first deposited layers (F.D.L) are illustrated in (a) and (b).
We also inverted the printing speeds of the inner and outer disks (i.e., the inner disk was printed at 80 mm s−1 and the outer at 20 mm s−1) (Fig. 3b). We observed that the final shape of the disk was highly dependent on the size of the inner and outer disks (Fig. 3b–left). For example, when 90% of the inner disk was printed with the highest speed, more defects were present in the inner part of the disk. Given that the outer disk was printed with the lowest speed and was, thus, defect-free, the structure was over-constrained and ended up developing a negative Gaussian curvature (i.e., \(K \, < \) 0 otherwise known as hyperbolic or saddle-like curvature) (Fig. 3b–right). In addition, we performed an experiment in which the size of the outer layer was kept constant while varying the printing speed. Such adjustments modified the overall shape of the disk (Supplementary Fig. S4). In conclusion, combining a rational distribution of defects with a proper spatial distribution of the printing speed enables us to endow the 4D printed specimens with a non-Euclidean metric, which, upon activation, causes the sheet to adopt a non-Euclidean shape (i.e., a sphere-like or a saddle-like shape)46.
The role of bi-material positioning
To further study the effects of the boundary conditions on the overall shape-shifting behavior of the specimens, we used multi-material 4D printing with a soft polymer (i.e., thermoplastic polyurethane or TPU) as the second material. The elastic modulus of TPU is an order of magnitude lower than that of PLA. It also does not exhibit the capability of storing residual stresses and relaxing them in the temperature range used in this study (i.e., 40 °C \( < \, {{{{{\rm{T}}}}}} \, < \) 100 °C) (Fig. 2c). We segmented the disk into two regions (i.e., inner and outer). The inner region was printed with the highest speed (i.e., 80 mm s−1), while the outer region was made of TPU (printing speed = 25 mm s−1). TPU does not show any shape transformation when the specimens are heated. The shape transformation of the PLA part can, therefore, be tuned by the amount of the soft material printed around it (Fig. 4a–left). These boundary effects also contributed to the formation of local curvatures in the 4D-printed multimaterial disks. When 40% of the disk was printed from TPU, the local curvatures were close to zero within the TPU part (i.e., no deformation), while a positive curvature (i.e., dome-like or spherical) appeared at the disk center (Fig. 4a–right). Decreasing the size of the TPU to 10% extended the range of achievable Gaussian and mean curvatures towards more negative and positive values (Fig. 4a–right). A comparable behavior was observed across various printing and TPU deposition patterns (Supplementary Figs. S1 and S5). We further demonstrated that the specific positioning of TPU did not affect the overall curvature profile (Supplementary Fig. S5c). For example, when the TPU ring was placed internally (i.e., in the inner ring), the global saddle-like curvature was achieved (Supplementary Fig. S5c-left). Placing PLA atop the TPU in the middle ring (Supplementary Fig. S5c-middle) affected the bending stiffness of the disk, resulting in diminished overall curvature. Hence, the synergy between multi-material printing and the strategic placement of imperfections effectively allows for the modulation of residual stresses and bending stiffnesses, thereby facilitating a wide range of curvature types (Supplementary Fig. S5c).”
The peripheral edge of the PLA disks was printed from a softer material (i.e., TPU) and its size was varied. Such designs resulted in diverse types of shape transformations depending on the size of the region printed from the soft phase (a–left). This multi-material design approach also altered the local mean and Gaussian curvatures of the shape-transformed specimens (a–right). Swapping the printing order of the soft and hard polymers such that the soft TPU was printed at the center of the disk completely changed the overall shape transformation of the disks (b–left) as well as the local curvature values (b–right) as compared to the case where the core of the disk was printed from the hard material. The first and last deposited layers are denoted as F.D.L and L.D.L, respectively.
We also further delved into the effects of printing patterns (Supplementary Fig. S1) and initial shape of the 2D plates (Supplementary Figs. S5a and S5b) on the overall shape of the 4D printed structures. Toward that end, we printed plates, as concentrically printed filaments, at a speed of 80 mm s−1. When exposed to high temperatures, independent from the printing patterns and the initial shape of the plates, they showed a dome-like out-of-plane deformation (Supplementary Figs. S1b, S5a, and S5b). When the multi-material approach was used (i.e., printing TPU at the boundaries of the plate regardless of the printing direction), the parts printed from TPU remained unaffected and created discontinuity at the boundaries of the plate. This led to similar negative Gaussian curvatures as observed in disks (Supplementary Figs. S1a-bottom and S1b-bottom).
We also switched the order of the hard and soft polymers, printing the inner part of the specimens from TPU while their outer ring was made of PLA. Since the TPU part of the disks could not spontaneously deform, a completely new type of shape transformation was observed (Fig. 4b–left). Changing the material order resulted in more positive values of \({\kappa }_{1}\) and \({\kappa }_{2}\) leading to more positive mean and Gaussian curvatures (Fig. 4b–right). In the other words, the magnitudes and signs of the mean and Gaussian curvatures were entirely shifted (\({K} \, > \) 0, \(H \, > \) 0) and the outer section of the disk deformed opposite to the build direction (Fig. 4b). These results clearly show the importance of rationally positioning the hard and soft polymers to tailor the local mean and Gaussian curvatures developed in the 4D printed objects.
We have so far shown that, in addition to programming the distribution of residual stress and imperfections density in-plane, these properties can also be adjusted across the section by changing the printing speed along the thickness of the disk. In Fig. 5a, position 1, the bottom layers of the disk were printed at a low speed (i.e., 20 mm s−1) while the upper layers were printed with a higher speed (i.e., 80 mm s−1). As the contraction is stronger in the upper layer, the concavity of the resulting cone is on the opposite side of the printing build-plate. Inverting the printing recipe results into a symmetric shape (the thickness of the specimens is large enough to hinder significant curling effect). In this case, the initial printing layers closer to the printing build-plate were made with the maximum printing speed (i.e., 80 mm s−1) while the top layers of the disk were printed with the lowest printing speed (i.e., 20 mm s−1) (Fig. 5a, position 2). In this way, we could also change the gradient of the expansion coefficients across the thickness. Transferring the imperfections to the top part of the specimens, adjusted the flexural rigidity of the disks and led to positive mean and Gaussian curvatures in the deformed state (i.e., inverse bending) (Fig. 5a–right).
The distribution of residual stresses across the thickness determines the bending orientation of the PLA disks. We introduced higher residual stress at the bottom layer of the PLA-disk (i.e., the surface which is in contact with the printing build-plate) by using a faster printing strategy for the initial layers. Such manipulation of the imperfection resulted in an inverse bending of the PLA disks (a–left, position 2) with an opposite localized curvature as compared to the case where the higher gradient was located at the top layer of the PLA disks (a–left, position 1). By precisely positioning the imperfections in the PLA disks and integrating the concept of inverse bending with that of out-of-plane deformation, one can achieve more complex shape transformations (b–left) (see Supplementary Movie 2 for the dynamic visualization of the shape-shifting process). Even more complex shapes can be achieved by including the soft polymeric phase in the design of the 4D printed disks with alternating the position of the residual stress (b–right). The distribution of the soft phase around the periphery of the PLA disks can also contribute to its overall shape-shifting behavior (c).
More complex shape transformations can be realized by combining both proposed approaches. For example, we attached two disks with different expansion factors and different imperfection distributions at their center point (Fig. 5b). The imperfections of the bottom disk were at the bottom, while those of the top disk were at the top, changing the gradient of the expansion factors across the thickness (Fig. 5b–left). The interaction between these two disks resulted in the bending of both disks in the opposite directions (Fig. 5b–left, Supplementary Movie 2). We also combined this design with multi-material printing to realize a 3D structure that formed a combination of a dome-like (i.e., spherical) and saddle-like (i.e., hyperbolic) geometries (Fig. 5b–right). Such complex types of shape transformations from a flat state are impossible to achieve with single material 4D printing.
We demonstrated that by introducing a second softer material into the design of 4D printed disks, one can change the local distribution of deformation within 4D printed objects. This can be done by constraining the deformation of the peripheral edges of the disk. The way in which the soft phase is distributed around the periphery of the disk could also influence its shape-shifting behavior (Fig. 5c). To demonstrate those effects, we segmented the disk into two, three, or four sections to which the soft polymeric material was assigned (Fig. 5c). The significant shape differences resulting from these designs confirm the utility of this strategy as an additional route for the adjustment of the shape transformation behavior of 4D printed disks.
Conclusion
We presented an approach in which we can control the differential deformation mechanisms in 4D printed structures. We were also able to control the spatial distributions of the printing imperfections and a second softer phase to achieve 4D printed structures with complex shape transformations and predictable final shapes. Our study also reveals the important underlying mechanisms responsible for the shape-shifting behavior of objects printed from SMPs using FDM-based 4D printing processes. One of these mechanisms is the formation of defects (voids) and residual strains during such printing processes. While such artifacts are often considered undesirable and their distributions are somewhat random at the level of individual filaments, their overall distributions at large enough length scales follow predictable patterns and are correlated with the parameters of the 4D printing process. We could, therefore, utilize the distribution of printing artifacts as one of the pillars of our proposed design strategy. This change in perspective in terms of how printing imperfections are seen can open up new opportunities for the design of defect-based metamaterials. The proposed designs have numerous potential applications of which one regarding the engineering of complex drug delivery systems or filters is highlighted here (Supplementary Movie 2). Our focus on the generation of complex curvature fields is partially motivated by the prominent role of curvature in biology47 and, thus, regenerative medicine as well as the importance of complex curvature in many technological areas, such as (soft) robotics48,49,50, medical instruments51,52, and structural engineering39,53,54.
Materials and methods
4D printing
We additively manufactured the disks (diameter = 55 mm) using PLA filaments (UltiMaker PLA-blue, 750 gr Natural with a filament diameter of 2.85 mm) for the hard and TPU for the soft phase using a fused deposition modeling (FDM) 3D printer (Ultimaker 3, Ultimaker B.V., The Netherlands). We customized the G-code for the 3D printing of the structures to adjust the printing parameters (i.e., printing speed, printing temperature, multi-material printing, etc.). We used nozzles with a diameter of 0.4 mm, a fixed bed printing temperature of 60 °C, a constant layer thickness of 0.15 mm, and a steady extrusion temperature of 200 °C for PLA and 225 °C for TPU. As the default option, we used 100% of the cooling capacity of the printer to maximize the amount of residual stress and the number of the introduced defects. In specific areas, such as the initial layers and at the PLA/TPU interface, we reduced the cooling rate and print speed to build a good foundation, smoothly connecting individual layers and creating proper attachment between the disk and the build-plate. The first four layers of the specimens (\(\sim\)25% of their thickness) were printed at a printing speed equal to 50% of their overall printing speed and were cooled using 50% of the cooling capacity of the printer (specimens in Figs. 1e–h, 3, 4, and 5c). For example, for the disks printed at the highest printing speed (i.e., 80 mm s−1), the first four layers were printed at 40 mm s−1 and a cooling capacity of 50% was used. At the interface of TPU and PLA (i.e., specimens in Fig. 4 and Fig. 5b–c), no cooling was used to improve the bonding of both materials and to achieve a higher printing quality.
For the specimens shown in Fig. 5a, we applied different configurations of printing speeds and cooling rates along their thicknesses to alternate the gradient of residual stress and program the side of concavity. Towards this aim, 25% of the specimens were printed with the lowest printing speed (i.e., 20 mm s−1) while the rest were printed with the highest (i.e., 80 mm s−1) (position 1 in Fig. 5a). To reverse the concavity, the bottom parts (75% of the overall thickness) of the specimens were printed with the highest printing speed (i.e., 80 mm s−1) while the top part was printed with the lowest (i.e., 20 mm s−1) (position 2 in Fig. 5a). In position 2, the initial layer was also printed at a speed of 40 mm s−1 with no print cooling.
In the specimens shown in Fig. 5b, we employed the printing strategy described in sub-Fig. 5a to print specimens 1 and 2 on top of each other. To print the specimens in one step, we placed an adhesive sheet (Tesa 4438 Blue Tape) between both disks in the middle of the printing process. Only a small section of the center (\({R}_{{in}}/R \sim\) 5%) was not covered by the adhesive sheet to connect the specimens. For the multi-material printed specimens, a composition ratio of \({V}_{{PLA}}/{V}_{{total}}=90 \%\) was used. This ratio was maintained constant unless otherwise stated.
Activation
We used a temperature-controlled bath with a heating immersion circulator (CORIO CD, Julabo, Germany) to activate the shape transformation process of the 4D printed specimens. The specimens were submerged in boiling water for a minimum of 60 s to ensure the shape-shifting process was fully completed. They were then cooled down to their initial room temperature.
Micro-computed tomography (μCT)
We used Phoenix X-ray Nanotom® (GE Sensing and Inspection Technologies GmbH, Wunstorf, Germany) for μCT imaging of the PLA specimens printed at two printing speeds (i.e., 20 and 80 mm s−1) and the TPU disks. The specimens were scanned over 360˚ using a voxel size of 25 µm and an angular rotation step of 1˚. The images were acquired at 110 kV and 160 µA for a total scan time of 24 min. We used Fiji (v 1.53) to analyze the acquired images and to calculate the porosity along the radius and depth of the specimens
3D optical scanning
The outer contour of the deformed structures was captured by a 3D scanner (Scan-In-A-Box, FX, DELL mini beamer, resolution of both cameras (IDS UI-3250LE-M-GL): 1600 × 1200 pixels). The specimens were photographed from at least eight different angles. The images were then rigidly registered using the software accompanying the 3D scanner (IDEA). After noise removal, the point clouds were imported into CloudCompare software (V.2.9.1) for further analysis.
Dynamic mechanical analysis (DMA)
A dynamic mechanical thermal analyzer (TA Instruments, Q800 DMA) was used to measure the time-, temperature-, and frequency-dependent mechanical properties of the 3D printed cuboid bar-like structures made from PLA (at two printing speeds, 20 and 80 mm s−1) and TPU. We designed and 3D printed bars (30 × 10 × 1.5 mm3) for force-controlled tensile DMA testing with a temperature ramp of 5 °C and at a constant frequency of force oscillation (1 Hz). From the \(\tan (\delta )\) and the storage modulus measured by the DMA, we derived the glass transition temperature and the temperature-dependent elastic moduli of the PLA and TPU. Under dynamic mechanical loading, the complex elastic modulus in terms of the storage, \({E}^{{\prime} }\), and loss modulus, \(E^{\prime \prime}\), is formulated as \({E}^{* }={E}^{{\prime} }+iE^{\prime \prime}\), where \(E^{\prime \prime}={E}^{{\prime} }\tan (\delta )\). Given the magnitude of the vector \({E}^{* }\), the magnitude of the temperature-dependent elastic modulus is calculated as \(E\left(T\right)={E}^{{\prime} }\sqrt{1+{\tan (\delta )}^{2}}\)55\(.\) We also measured the glass transition temperature of the specimens, which was defined as the temperature corresponding to the peak value of \(\tan (\delta )\).
Measurement of expansion factors
We measured the expansion factors along the printing direction (\({\beta }_{1}\)= longitudinal expansion factor) and perpendicular to the printing direction (\({\beta }_{2}\)= transverse expansion factor) using Eq. (2) (Fig. 1b) for PLA specimens printed at different printing speeds (Fig. 1c) and thicknesses (Fig. 2b). Although the actual shape transformation is not, from a physics viewpoint, a thermal expansion effect, it is numerically expedient to model it through a standard heat expansion routine with orthotropic expansion coefficients. We extracted the \({\alpha }_{1}\) and \({\alpha }_{2}\) values from the longitudinal and transverse expansion coefficients (\({\beta }_{1}\) and \({\beta }_{2}\)):
The parameter \({\alpha }_{3}\) was measured by comparing the thickness of the samples before and after thermal actuation. We also assumed that TPU is an incompressible material and employed orthotropic thermal expansion coefficients to ensure that its volume did not change after being exposed to high temperatures (see Supplementary Table S1).
Computational modeling
Finite element modeling was conducted using the commercial software suite Abaqus (Dassault Simulia, V6.14, USA). We used linear thermally-coupled brick elements with full integration points in three directions (C3D8T, Abaqus). We uniformly applied the temperature with a magnitude of 100 °C \(({=T}_{{ambient}}+\triangle T)\) to perform a coupled temperature–displacement steady-state analysis. In order to mimic the anisotropic relaxation we observed above the glass transition temperature, we considered temperature-dependent elastic moduli \((E\left(T\right))\) and orthotropic thermal expansion coefficients as the material model in our computational models. These values were obtained from experimental data and are presented in Supplementary Tables S1 and S2.
We applied a symmetric boundary condition which enabled us to model half of the disk. The center of the disk was fixed. The model was discretized using five elements in thickness and radial elements with a size of 700 µm. The imperfections were introduced into the computational models by assigning extremely low mechanical properties (i.e., \(E=1{Pa}\)) to certain elements of the disk to trigger the instabilities in the system after applying the load56,57,58. The imperfections were distributed systematically to imitate the same distribution patterns as seen in the μCT images. The porosity of the PLA specimens printed at 80 mm s−1 was increased in both radial and build directions (Fig. 2e–f), assuming that the initial layer (20% of thickness) was effectively defect-free. The imperfections were, therefore, implemented every \(\sim\)2.1 mm between \({R}_{{in}}/R \sim\)30% (this number can be \(\sim\)15% for the top layers) and \({R}_{{in}}/R \sim\)100% (i.e., the peripheral edge of the specimens) (Supplementary Figure S3a).
The sensitivity of the FE models to the distribution of the imperfections was analyzed computationally. We observed that the defects were not distributed uniformly at each layer (Fig. 2d). We, therefore, implemented a non-symmetric distribution of the imperfections in the angular direction and examined the effects of varying the angle of the imperfection distribution (\(\gamma\)) (i.e., from 30° to 150°) on the shape-shifting behavior of the constructs. Our results showed that the imperfection distribution in the angular direction (\(\gamma\)) does not significantly affect the cone angle (\(\theta\)) (Supplementary Figure S3b). We considered the distribution of imperfections with \(\gamma =120^\circ\) in our model. A good agreement was achieved between the proposed computational model and our experimental observations (Supplementary Figure S3c).
Curvature measurements
The principal surface curvatures were estimated from the triangulated meshes obtained through 3D scanning, using a surface fitting-based algorithm that was implemented in a recent mesh processing workflow59. Briefly, the robust curvature estimation algorithm in the Python-based libigl toolbox was used, which estimates the curvature at every vertex by fitting a second-order polynomial to a local neighborhood and quantifying the curvature using the fitted surface patch60,61. The local neighborhood is defined as a spherical region with the radius \(r\). We initially screened a range of values for \(r\) and found that \(r=15\left\langle e\right\rangle\), where \(\left\langle e\right\rangle\) is the average edge length in the mesh, results in an appropriate balance between detecting the curvature of very small mesh features and only capturing the macroscale curvature of the structure. The principal curvatures \({\kappa }_{1}\) and \({\kappa }_{2}\) were then used to compute the mean \((H=\frac{1}{2}({\kappa }_{1}+{\kappa }_{2}))\) and Gaussian (\(K={\kappa }_{1}{\kappa }_{2}\)) curvatures that are reported in the main text. To obtain non-dimensional curvature quantities, the curvature values were normalized using a characteristic length \({S}_{v}=\frac{V}{S}\), where \(V\) is the volume of the smallest rectangular box containing the specimen and \(S\) is the mesh surface area59. The 3D mesh reconstructions, color-coded by curvature, were visualized using Paraview.
Data availability
The data that support the findings of this study are available within this manuscript and its Supplementary Materials.
References
c.l.f.u. lierre/universcience/amàco, Drying a thin slice of wood, 2015. https://vimeo.com/175694172. (Accessed June 2022.
P. Oudet, Art in wood, 2022. http://www.lavieenbois.com. (Accessed June 2022)
Rees, W. M. V., Vouga, E. & Mahadevan, L. Growth patterns for shape-shifting elastic bilayers. Proc. Natl. Acad. Sci. 114, 11597–11602 (2017).
Boley, J. W. et al. Shape-shifting structured lattices via multimaterial 4D printing. Proc. Natl. Acad. Sci. 116, 20856–20862 (2019).
Gonzalez-Bellido, P. T., Scaros, A. T., Hanlon, R. T. & Wardill, T. J. Neural Control of Dynamic 3-Dimensional Skin Papillae for Cuttlefish Camouflage. iScience 1, 24–34 (2018).
Gosline, J. M. & DeMont, M. E. Jet-propelled swimming in squids. Sci. American 252, 96–103 (1985).
Armon, S., Efrati, E., Kupferman, R. & Sharon, E. Geometry and Mechanics in the Opening of Chiral Seed Pods. Science 333, 1726–1730 (2011).
Yang, Y. et al. Recent Progress in Biomimetic Additive Manufacturing Technology: From Materials to Functional Structures. Adv. Mater. 30, 1706539 (2018).
Kim, H. et al. Shape morphing smart 3D actuator materials for micro soft robot. Mater. Today 41, 243–269 (2020).
Sun, Y. et al. Design and fabrication of a shape-morphing soft pneumatic actuator: Soft robotic pad. IEEE/RSJ Int. Confer. Intell. Robots Syst. (IROS) 2017, 6214–6220 (2017). pp.
Bertoldi, K., Vitelli, V., Christensen, J. & van Hecke, M. Flexible mechanical metamaterials. Nat. Rev. Mater. 2, 1–11 (2017).
Wenz, F. et al. Designing Shape Morphing Behavior through Local Programming of Mechanical Metamaterials. Adv. Mater. 33, 2008617 (2021).
Coulais, C., Teomy, E., de Reus, K., Shokef, Y. & van Hecke, M. Combinatorial design of textured mechanical metamaterials. Nature 535, 529–532 (2016).
Jiang, C., Rist, F., Wang, H., Wallner, J. & Pottmann, H. Shape-morphing mechanical metamaterials. Comput-Aided Design 143, 103146 (2022).
Jin, L. et al. Guided transition waves in multistable mechanical metamaterials. Proc. Natl. Acad. Sci. 117, 2319–2325 (2020).
Mirzaali, M., Janbaz, S., Strano, M., Vergani, L. & Zadpoor, A. A. Shape-matching soft mechanical metamaterials. Sci. Rep. 8, 1–7 (2018).
Hajiesmaili, E. & Clarke, D. R. Reconfigurable shape-morphing dielectric elastomers using spatially varying electric fields. Nat. Commun. 10, 183 (2019).
Zhang, J. et al. Liquid Crystal Elastomer-Based Magnetic Composite Films for Reconfigurable Shape-Morphing Soft Miniature Machines. Adv. Mater. 33, 2006191 (2021).
Xu, W., Kwok, K. S. & Gracias, D. H. Ultrathin Shape Change Smart Materials. Acct. Chem. Res. 51, 436–444 (2018).
Hilber, W. Stimulus-active polymer actuators for next-generation microfluidic devices. Appl. Phys. A 122, 751 (2016).
Gu, J. et al. Geodesy: Self-rising 2.5D Tiles by Printing along 2D Geodesic Closed Path, Proceedings of the 2019 CHI Conference on Human Factors in Computing Systems, Association for Computing Machinery, Glasgow, Scotland Uk, 2019, p. Paper 37.
Xia, Y., He, Y., Zhang, F., Liu, Y. & Leng, J. A Review of Shape Memory Polymers and Composites: Mechanisms, Materials, and Applications. Adv. Mater. 33, 2000713 (2021).
Bastola, A. K., Paudel, M. & Li, L. Dot-patterned hybrid magnetorheological elastomer developed by 3D printing. J. Magnet. Magnetic Mater. 494, 165825 (2020).
Yarali, E. et al. Magneto‐/ electro‐responsive polymers toward manufacturing, characterization, and biomedical/ soft robotic applications, Applied. Materials Today 26, 101306 (2022).
Aharoni, H., Xia, Y., Zhang, X., Kamien, R. D. & Yang, S. Universal inverse design of surfaces with thin nematic elastomer sheets. Proc. Natl. Acad. Sci. 115, 7206–7211 (2018).
Champeau, M. et al. 4D Printing of Hydrogels: A Review. Adv. Funct. Mater. 30, 1910606 (2020).
Dong, Y. et al. 4D Printed Hydrogels: Fabrication, Materials, and Applications. Adv. Mater. Technol. 5, 2000034 (2020).
Gao, T., Siéfert, E., DeSimone, A. & Roman, B. Shape Programming by Modulating Actuation over Hierarchical Length Scales. Adv. Mater. 32, 2004515 (2020).
Mailen, R. W. et al. Thermo-mechanical transformation of shape memory polymers from initially flat discs to bowls and saddles. Smart Mater. Struct. 28, 045011 (2019).
Cui, J., Poblete, F. R. & Zhu, Y. Origami/Kirigami-Guided Morphing of Composite Sheets. Adv. Funct. Mater. 28, 1802768 (2018).
Andres, C. M., Zhu, J., Shyu, T., Flynn, C. & Kotov, N. A. Shape-Morphing Nanocomposite Origami. Langmuir 30, 5378–5385 (2014).
Jin, L., Forte, A. E., Deng, B., Rafsanjani, A. & Bertoldi, K. Kirigami-Inspired Inflatables with Programmable Shapes. Adv. Mater. 32, 2001863 (2020).
Choi, G. P. T., Dudte, L. H. & Mahadevan, L. Programming shape using kirigami tessellations. Nat. Mater. 18, 999–1004 (2019).
Neville, R. M., Scarpa, F. & Pirrera, A. Shape morphing Kirigami mechanical metamaterials. Sci. Rep. 6, 31067 (2016).
Aharoni, H., Sharon, E. & Kupferman, R. Geometry of Thin Nematic Elastomer Sheets. Phys. Rev. Lett. 113, 257801 (2014).
Li, Z. et al. Analytical study on growth-induced axisymmetric deformations and shape-control of circular hyperelastic plates. Int. J. Engineer. Sci. 170, 103594 (2022).
Barletta, M., Gisario, A. & Mehrpouya, M. 4D printing of shape memory polylactic acid (PLA) components: Investigating the role of the operational parameters in fused deposition modelling (FDM). J. Manufact. Proc. 61, 473–480 (2021).
van Manen, T., Janbaz, S. & Zadpoor, A. A. Programming the shape-shifting of flat soft matter. Mater. Today 21, 144–163 (2018).
Gladman, A. S., Matsumoto, E. A., Nuzzo, R. G., Mahadevan, L. & Lewis, J. A. Biomimetic 4D printing. Nat. Mater. 15, 413–418 (2016).
Zhang, Q., Zhang, K. & Hu, G. Smart three-dimensional lightweight structure triggered from a thin composite sheet via 3D printing technique. Sci. Rep. 6, 22431 (2016).
Timoshenko, S. Analysis of bi-metal thermostats. Josa 11, 233–255 (1925).
van Manen, T., Janbaz, S. & Zadpoor, A. A. Programming 2D/3D shape-shifting with hobbyist 3D printers. Materials Horizons 4, 1064–1069 (2017).
Janbaz, S., Hedayati, R. & Zadpoor, A. A. Programming the shape-shifting of flat soft matter: from self-rolling/self-twisting materials to self-folding origami. Materials Horizons 3, 536–547 (2016).
Ding, Z., Weeger, O., Qi, H. J. & Dunn, M. L. 4D rods: 3D structures via programmable 1D composite rods. Mater. Design 137, 256–265 (2018).
Wan, X., He, Y., Liu, Y. & Leng, J. 4D printing of multiple shape memory polymer and nanocomposites with biocompatible, programmable and selectively actuated properties. Additive Manufact. 53, 102689 (2022).
Klein, Y., Efrati, E. & Sharon, E. Shaping of Elastic Sheets by Prescription of Non-Euclidean Metrics. Science 315, 1116–1120 (2007).
Callens, S. J., Uyttendaele, R. J., Fratila-Apachitei, L. E. & Zadpoor, A. A. Substrate curvature as a cue to guide spatiotemporal cell and tissue organization. Biomaterials 232, 119739 (2020).
Santina, C. D. & Rus, D. Control Oriented Modeling of Soft Robots: The Polynomial Curvature Case. IEEE Robot. Automat. Lett. 5, 290–298 (2020).
Rus, D. & Tolley, M. T. Design, fabrication and control of soft robots. Nature 521, 467–475 (2015).
Wang, H., Totaro, M. & Beccai, L. Toward Perceptive Soft Robots: Progress and Challenges, Advanced. Science 5, 1800541 (2018).
Khan, F., Donder, A., Galvan, S., Baena, F. R. Y. & Misra, S. Pose Measurement of Flexible Medical Instruments Using Fiber Bragg Gratings in Multi-Core Fiber. IEEE Sensors J. 20, 10955–10962 (2020).
De Greef, A., Lambert, P. & Delchambre, A. Towards flexible medical instruments: Review of flexible fluidic actuators. Prec. Engineer. 33, 311–321 (2009).
Mirzaali, M. J. et al. Curvature Induced by Deflection in Thick Meta-Plates. Adv. Mater. 33, 2008082 (2021).
Yuan, C., Wang, F. & Ge, Q. Multimaterial direct 4D printing of high stiffness structures with large bending curvature. Extreme Mech. Lett. 42, 101122 (2021).
Bodaghi, M., Damanpack, A. R. & Liao, W. H. Adaptive metamaterials by functionally graded 4D printing. Mater. Design 135, 26–36 (2017).
Nikravesh, S., Ryu, D. & Shen, Y.-L. Direct numerical simulation of buckling instability of thin films on a compliant substrate. Adv. Mech. Engineer. 11, 1687814019840470 (2019).
Nikravesh, S., Ryu, D. & Shen, Y.-L. instabilities of thin films on a compliant Substrate: Direct numerical Simulations from Surface Wrinkling to Global Buckling. Sci. Rep. 10, 1–19 (2020).
van Manen, T., Dehabadi, V. M., Saldívar, M. C., Mirzaali, M. J. & Zadpoor, A. A. Theoretical stiffness limits of 4D printed self-folding metamaterials. Commun Mater. 3 (2022).
Callens, S. J. P., Tourolle Ne Betts, D. C., Muller, R. & Zadpoor, A. A. The local and global geometry of trabecular bone. Acta Biomater 130, 343–361 (2021).
Panozzo, D., Puppo, E. & Rocca, L. Efficient multi-scale curvature and crease estimation, 2nd International Workshop on Computer Graphics, Computer Vision and Mathematics, GraVisMa 2010 - Workshop Proceedings, 2010, pp. 9–16.
Jacobson, A. et al. libigl: A simple C++ geometry processing library, (2016).
Adibaskoro, T., Makowska, M., Rinta-Paavola, A., Fortino, S. & Hostikka, S. Elastic Modulus, Thermal Expansion, and Pyrolysis Shrinkage of Norway Spruce Under High Temperature. Fire Technol. 57, 2451–2490 (2021).
Acknowledgements
M.J.M. acknowledges funding from Open Competition Domain Science – XS, NWO and Idea Generator (NWA-IDG) research program with code numbers NWA.1228.192.228. M.H. acknowledges funding from the Netherlands Organization for Scientific Research through NWO-VIDI grant No. 680-47-548/983. J.B. acknowledges funding from the French Agence Nationale de la Recherche, project SecondSkin.
Author information
Authors and Affiliations
Contributions
M.J.M., V.M., M.H., and A.A.Z. designed the research. V.M., E.Y., and T.M. performed numerical simulations. V.M. performed experiments (3D and μCT scan). V.M. performed image analyses and data collection from numerical simulations and 3D scans. S.J.P.C. performed surface curvature measurements. J.B, and M.H developed the theoretical models. V.M., E.Y., A.G., A.A., and S.G., performed dynamic mechanical testing. V.M., M.J.M., J.B, M.H. and A.A.Z. performed the data analysis and interpretation. V.M., and M.J.M. performed data visualizations. M.J.M., J.B., M.H., and A.A.Z. wrote the manuscript. All the authors critically revised the manuscript for its intellectual content and approved the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Communications Materials thanks the anonymous reviewers for their contribution to the peer review of this work. Primary Handling Editor: Aldo Isidori. A peer review file is available.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Moosabeiki, V., Yarali, E., Ghalayaniesfahani, A. et al. Curvature tuning through defect-based 4D printing. Commun Mater 5, 10 (2024). https://doi.org/10.1038/s43246-024-00448-w
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s43246-024-00448-w