Crystal electric field level scheme leading to giant magnetocaloric effect for hydrogen liquefaction

Abstract

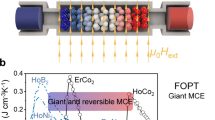
In recent years, magnetic refrigeration has attracted considerable attention for hydrogen liquefaction. Most materials used for magnetic refrigeration contain heavy rare earth ions with complex crystalline electric field energy splittings, whose effect on the magnetic entropy change ΔS_M has not been systematically studied. In particular, the theoretical upper limits of ∣ΔS_M∣ for general heavy earth cases are unknown. Here, we show that the crystalline electric field level schemes result in a large ΔS_M for general heavy rare earth cases. We provide a specific example of the magnetic refrigeration material HoB₂ using inelastic neutron scattering experiments combined with mean-field calculations with crystal field splitting and exchange interactions. The relationship between ΔS_M and crystal field parameters presented in this study can be useful for developing compounds with a large ∣ΔS_M∣ and advancing the design of magnetic refrigeration materials.

Introduction

Liquid hydrogen (LH₂) is expected to be widely used as a medium for storing renewable energy. Although LH₂ allows hydrogen to be stored at the highest density among all media, it suffers a major technical bottleneck in terms of its cooling method. The cooling efficiency of the conventional gas compression technique is significantly lower at the hydrogen condensation temperature (20 K) compared to that at ambient temperatures¹. In recent years, magnetic refrigeration, a method employed to cool matter using magnetic fields via the magnetocaloric (MCE) effect, has been extensively studied as an alternative technique to conventional gas compression cooling for hydrogen liquefaction². In magnetic refrigeration, the magnetic field variation changes the quantity of heat in magnetic refrigeration materials³. Therefore, the MCE, which is identified by the change in the magnetic entropy with the change in the magnetic field (ΔS_M), is an important factor in a magnetic refrigeration cooling system. In this context, magnetic refrigeration materials with a large absolute value of ΔS_M (i.e., ∣ΔS_M∣) have been investigated to improve the magnetic refrigeration cooling performance^4,5.

Conventional guidelines for developing magnetic refrigeration materials are based on the following ideas: (i)Materials should contain heavy rare earth ions with a large total angular momentum (J), considering a large magnetic entropy is potentially caused by the number of states owing to the magnetic entropy obeying S_M = RIn(2J + 1) (R is the molar gas constant). (Although some rare earth elements are classified as critical materials, the amount of usage for magnetic refrigeration materials is expected to be insignificant.) (ii) Materials should possess ferromagnetic exchange interactions with several tens of kelvin order giving a ferromagnetic phase transition temperature (T_C) above 20 K, given that ΔS_M normally shows a maximum value around T_C. When using liquid nitrogen for pre-cooling hydrogen for liquefaction, T_C should be in the 20–77 K range. Additionally, the internal magnetic field due to the ferromagnetic exchange interactions enables additional splitting of crystalline electric field (CEF) levels to Zeeman splitting with an external magnetic field, which significantly decreases the number of states.

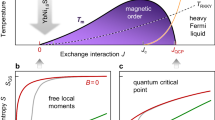
However, many attempts at developing materials with a large ΔS_M have been unsuccessful owing to the large reduction in degeneracy by the CEF effect even at zero magnetic fields. One may naturally consider that Gd³⁺ (J = 7/2), which maintains an eight-fold degeneracy in any CEF can be the best choice to obtain a large ∣ΔS_M∣ because of the S-state of the half-filled 4f shell. This can be true only when the thermal energy (k_BT) is negligibly small compared to that in the magnetic Zeeman splitting (μ₀MH). In this case, μ₀MH/k_BT ≫ 1, and the degeneracy can be completely lifted by a small magnetic field (Fig. 1a). In fact, for extremely low-temperature (T < 1 K) cooling with adiabatic demagnetization refrigeration (ADR), paramagnetic Gd³⁺ compounds such as Gd₂(SO₄)₃ ⋅ 8H₂O and Gd₃Ga₅O₁₂ are used^6,7,8. In contrast, considering magnetic refrigeration materials for cooling around room temperature (T ~ 300 K), i.e., μ₀MH/k_BT ≪ 1, one cannot largely change S_M in a magnetic field region up to ~ 5 T. (Fig. 1b). Nevertheless, some ferromagnets can be used as room-temperature magnetic refrigeration materials considering largely induced magnetization by a small magnetic field around T_C can significantly assist the external magnetic field (H) with the internal molecular field originating from exchange interactions, H_ex, expressed by μ₀M(H + H_ex)/k_BT ~ 1 (Fig. 1b)^3,9.

Fig. 1: Summary of the relationship between Zeemann splitting of energy level and magnetic entropy change for different temperature ranges.

Zeemann splitting of energy level and magnetic entropy change of Gd³⁺ at aT = 1 K, bT = 300 K, and c T = 20 K. μ₀mH_ex denotes the exchange interaction energy. In d Zeemann splitting of Er³⁺ and e magnetic entropy changes for Dy³⁺, Ho³⁺, and Er³⁺ for ideal case of crystalline electric field parameters when compared to the Gd³⁺ case. They are calculated with the mean-field theory, which is described in the main text.

In contrast, at intermediate temperatures of several tens of kelvin, including the hydrogen liquefaction temperature (20.3 K), heavy rare earth compounds such as HoAl₂^10,11,12,13 and ErCo₂^5,14 can be used as magnetic refrigeration materials, in addition to Gd compounds. The CEF level scheme is considered important for understanding magnetism and the MCE of individual materials in this temperature range owing to the CEF level splitting compared to those at the system temperature¹⁵. However, the relationship between the CEF level scheme and the MCE in heavy rare earth cases at temperatures of several tens of kelvin has not been studied for magnetic refrigeration materials design. Therefore, considering the recently growing societal demand for hydrogen liquefaction as an energy storage medium, it is necessary to study magnetic refrigeration materials based on heavy rare earth systems with a large MCE.

This study investigated the relationship between the CEF level scheme and a giant MCE in the hydrogen liquefaction temperature range. First, we show the CEF level scheme of holmium diboride (HoB₂) by combining inelastic neutron scattering experiments and mean-field calculations of the exchange interaction with the CEF. Recently, HoB₂ has shown very large ∣ΔS_M∣ values (0.35 J cm⁻³ K⁻¹ at 15 K and 5 T) near the hydrogen liquefaction temperature⁴. Although its ∣ΔS_M∣ value is much larger than most magnetic refrigeration materials, except in some rare cases such as ErCo₂ (0.37 J cm⁻³ K⁻¹)¹⁴ and HoN (0.29 J cm⁻³ K⁻¹)¹⁶, the origin of the giant MCE has not yet been understood owing to the unknown CEF level scheme. Second, we introduce ideal CEF level schemes that lead to a giant MCE for general heavy rare earth systems in the hydrogen liquefaction temperature range based on mean-field calculations.

The results show that the CEF level schemes of ground-state J-multiplets in heavy rare earth systems significantly influence how the degeneracy is lifted by a magnetic field through Zeeman splitting, considering the CEF energy levels are comparable to the thermal energy k_BT of the system temperature (Fig. 1c). Furthermore, we show that an extremely large ΔS_M ~ − 12 J mol⁻¹  K⁻¹ can be obtained at 20 K (Fig. 1e) by choosing appropriate CEF parameters in Dy, Ho, and Er compounds, which provide a CEF level scheme with a highly degenerated ground state in a zero field and an isolated state in a magnetic field (Fig. 1d). Lastly, we conclude that it is necessary to develop additional guidelines based on the CEF level scheme to design magnetic refrigeration materials for hydrogen liquefaction.

Results and discussion

Crystal electric field level scheme in HoB₂

Because the Ho³⁺ ion in HoB₂ is placed in an electrostatic potential with hexagonal D_6h point group symmetry at the (0,0,0) position of the P6/mmm space group, the ground state of the J-multiplets ⁵I₈ (J = 8, S = 2, L = 6) of the 4f electrons of Ho³⁺ splits into eleven states (five singlets (${\Gamma }_{1}^{{{{{{{{\rm{A,B}}}}}}}}},{\Gamma }_{2},{\Gamma }_{3},{\Gamma }_{4}$,) and six doublets (${\Gamma }_{5}^{{{{{{{{\rm{A,B,C}}}}}}}}},{\Gamma }_{6}^{{{{{{{{\rm{A,B,C}}}}}}}}}$)) by the CEF interaction with the hexagonal symmetry D_6h¹⁷. This splitting can be expressed by the phenomenological CEF Hamiltonian, as:

$${{{{{{{{\mathcal{H}}}}}}}}}_{{{{{{{{\rm{CEF}}}}}}}}}({D}_{6h})={B}_{2}^{0}{O}_{2}^{0}+{B}_{4}^{0}{O}_{4}^{0}+{B}_{6}^{0}{O}_{6}^{0}+{B}_{6}^{6}{O}_{6}^{6}$$

(1)

where the coefficients ${B}_{l}^{m}$ are the CEF parameters and ${O}_{l}^{m}$ are Steven’s operator equivalents, which are expressed by polynomials of components of the total angular momentum operators¹⁸. Therefore, we experimentally determine the four ${B}_{l}^{m}$ parameters to in turn determine the CEF level scheme in HoB₂.

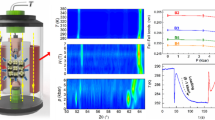
In an INS experiment, the CEF energy levels can be observed by measuring the energy spectrum in the paramagnetic phase (T ≥ T_C = 15 K) because of the absence of an internal magnetic field generated by ferromagnetic long-range ordering. The INS spectra at 20 K for incident neutron energies of ϵ_i= 10.16 and 39.97 meV are shown in Fig. 2a, b, respectively. The neutron intensities, which were subtracted with the data measured with the empty aluminum sample holder, are observed only below an energy transfer level of ~ 8 meV. Higher energy spectra observed in the ϵ_i = 102.3 meV experiment were only phonon modes in origin (Supplementary Fig. 1). By integrating the neutron intensities for the appropriate Q ranges, we obtained the energy spectra for the ϵ_i = 10.16 and 39.97 meV data (figures on the right in Fig. 2a, b). Several broad peaks were found around 1.0, 2.5, 5.0, and 7.5 meV, which were named P₁, P₂, P₃, and P₄, respectively. The INS intensity of the four excitation peaks can be fitted by the square of the Ho³⁺ magnetic form factor, which indicates that they are magnetic (CEF excitations) in origin (Fig. 2c, d).

Fig. 2: Inelastic neutron intensity maps at T = 20 K in HoB₂.

INS intensity maps with the line profile integrated along Q direction, I(E), measured at T = 20 K for the initial neutron energy of a ϵ_i = 10.16 meV and b ϵ_i = 39.97 meV. The Q dependence of the neutron intensity integrated along E-direction for c ϵ_i = 10.16 meV and (d)ϵ_i= 39.97 meV. The solid lines in (c) and (d) denote the curve of squared magnetic form factor, f²(κ), of Ho³⁺.

To identify the four independent ${B}_{l}^{m}$ parameters in HoB₂, we compared the experimental spectra (measured with ϵ_i = 10.16 meV and 39.97 meV at 20 K) to the calculated spectra described in Methods section. We chose to search a reasonable parameter space ($-1.0\le {B}_{2}^{0}/{k}_{{{{{{{{\rm{B}}}}}}}}}\le 1.0,-1.0\times 1{0}^{-3}\le {B}_{4}^{0}/{k}_{{{{{{{{\rm{B}}}}}}}}}\le 1.0\times 1{0}^{-3}, -1.0\times 1{0}^{-4}\le {B}_{6}^{0}/{k}_{{{{{{{{\rm{B}}}}}}}}}\le 1.0\times 1{0}^{-4},-1.0\times 1{0}^{-3}\le {B}_{6}^{6}/{k}_{{{{{{{{\rm{B}}}}}}}}}\le 1.0 \times 1{0}^{-3}$ in Kelvin), which was expected from the observed CEF spectrum confined below ~ 8 meV. We found the best parameter set that could explain the INS spectra observed at 20 K, i.e., ${B}_{2}^{0}/{k}_{{{{{{{{\rm{B}}}}}}}}}=0.11\pm 0.01$ (K), ${B}_{4}^{0}/{k}_{{{{{{{{\rm{B}}}}}}}}}=-0.40\pm 0.08$ (10⁻³ K), ${B}_{6}^{0}/{k}_{{{{{{{{\rm{B}}}}}}}}}=0.20\pm 0.01$ (10⁻⁴ K), and ${B}_{6}^{6}/{k}_{{{{{{{{\rm{B}}}}}}}}}=0\pm 0.07$ (10⁻⁴K), which produces the CEF level scheme in Fig. 3a. Figure 3b shows the comparison between the observed and calculated spectrum with the determined CEF parameters for several temperatures. In this fitting, we used the Lorentzian spectral function with the full width at the half maximum (FWHM) instead of the δ-function, which is described in Methods section. The natural FWHM was determined to be 0.56 meV at 20 K due to a finite dispersion relation originating from the ferromagnetic exchange interaction.

Fig. 3: Comparison of the observed neutron scattering intensity to the theoretical results calculated with the refined CEF parameters in HoB₂.

a The determined CEF level scheme of HoB₂. The single and double lines denote the singlet and doublet CEF levels, respectively, b comparison of the neutron scattering intensity between observation and calculation. The circle and triangle symbols denote the observed data for ϵ_i = 10.16 meV and ϵ_i = 39.97 meV. The solid lines are theoretical curves calculated by eq. (4) with the refined CEF parameters described in the main text. These curves were convoluted by the experimental resolution function, and c calculated neutron intensities (expressed by eq. (4)) for energy corresponding to each transition between two states at T = 20 K.

The determined CEF level scheme and the CEF states represented by the eigenstates of ${J}_{z},\left\vert m\right\rangle$ are summarized in Table 1. Although the CEF ground state was determined to be the singlet ${\Gamma }_{1}^{{{{{{{{\rm{B}}}}}}}}}$, two doublet excited states ${\Gamma }_{6}^{{{{{{{{\rm{C}}}}}}}}}$ and ${\Gamma }_{6}^{{{{{{{{\rm{B}}}}}}}}}$ at 0.932 meV and 0.937 meV, respectively, are nearly degenerated with the ground state considering a system temperature of 20 K (k_BT = 1.72 meV). The other excited states, such as ${\Gamma }_{1}^{{{{{{{{\rm{A}}}}}}}}},{\Gamma }_{2}$, and ${\Gamma }_{5}^{{{{{{{{\rm{C}}}}}}}}}$, are well separated by a level greater than ~ 3 meV. Therefore, we can approximately consider the quasi-quintuple ground state, including ${\Gamma }_{1}^{{{{{{{{\rm{B}}}}}}}}},{\Gamma }_{6}^{{{{{{{{\rm{C}}}}}}}}}$, and ${\Gamma }_{6}^{{{{{{{{\rm{B}}}}}}}}}$ at 20 K. By calculating the Zeeman splitting with the application of the magnetic field, we can see a significant decrease in the degeneracy from the quasi-quintuple state to the isolated singlet ground state with a large energy gap at μ₀H = 5 T (Fig. 4b). The result shows that the magnetic entropy can be largely altered by applying a magnetic field, which will be discussed shortly.

Table 1 List of the representation, eigenenergy and eigenstate in the CEF level scheme of HoB₂.

Fig. 4: Results of mean-field calculation with the experimentally determined CEF parameters in HoB₂.

a Temperature dependence of the inverse magnetic susceptibility along the principal directions, (b) Zeemann splittings of energy levels at 20 K, c magnetic entropy changes (ΔS_M) at 15 K and (d) magnetizations below 20 K in magnetic fields perpendicular and parallel to the hexagonal c-axis. Open circle symbols in c, and d the experimental data at 17 K taken from ref. ⁴. The inset in (c) shows the temperature dependence of ΔS_M when the magnetic field is change from 0 to 5 T.

Furthermore, we calculated the change in magnetic entropy by standard self-consistent mean-field calculation using the CEF parameters determined in the INS experiment for HoB₂. The mean-field approximation cannot exactly explain the critical behaviors of physical quantities near a phase transition. Nevertheless, because the MCE of rare-earth compounds has been successfully reproduced by the mean-field approximation^11,19,20, we used this approximation to explain the MCE of HoB₂ and general rare-earth systems. The mean-field Hamiltonian that includes the CEF (eq. (2)) term and additional magnetic term ${{{{{{{{\mathcal{H}}}}}}}}}_{{{{{{{{\rm{mag}}}}}}}}}$ is expressed as:

$${{{{{{{{\mathcal{H}}}}}}}}}_{{{{{{{{\rm{total}}}}}}}}}={{{{{{{{\mathcal{H}}}}}}}}}_{{{{{{{{\rm{CEF}}}}}}}}}+{{{{{{{{\mathcal{H}}}}}}}}}_{{{{{{{{\rm{mag}}}}}}}}},$$

(2)

$${{{{{{{{\mathcal{H}}}}}}}}}_{{{{{{{{\rm{mag}}}}}}}}}=-g{\mu }_{B}({\mu }_{0}{{{{{{{\boldsymbol{H}}}}}}}}+\lambda g{\mu }_{B}\langle {{{{{{{\boldsymbol{J}}}}}}}}\rangle )\cdot {{{{{{{\boldsymbol{J}}}}}}}},$$

(3)

where g, μ_B, H, and J are the Landé g-factor, Bohr magneton, external magnetic field, and total angular momentum operator, respectively. Definitions of the physical quantities, magnetization, specific heat and entropy as calculated by the mean-field calculation are provided in the Methods section.

For the case wherein the magnetic susceptibility along the easy axis becomes infinite at T_C = 15 K at the second-order magnetic phase transition from the paramagnetic to the ferromagnetic phase, the mean-field exchange parameter λ was estimated to be 0.62 T μ_B⁻¹. The temperature dependence of the inverse magnetic susceptibility perpendicular and parallel to the hexagonal c-axis is shown in Fig. 4a. The magnetic susceptibility in the hexagonal ab plane is slightly higher than that along the c-axis. The estimated anisotropy, χ_∣∣c/χ_⊥c = 0.97 (at 300 K), in HoB₂ was substantially low compared to that of most rare earth compounds, such as HoNi₅¹⁷ and DyAl₂²⁰.

Using the CEF and λ parameters determined for HoB₂, we calculated the magnetic field dependence of Zeeman splitting along the crystallographic directions at 20 K, as shown in Fig. 4b. While the quasi-quintuple ground state (${\Gamma }_{1}^{B},{\Gamma }_{6}^{C}$, and ${\Gamma }_{6}^{B}$) is formed in zero field, the degeneracy in a finite field is lifted by applying a magnetic field, and the ground state becomes isolated. When the field direction is perpendicular to the hexagonal c-axis, the singlet state ${\Gamma }_{1}^{B}$ significantly deviates from the other states because the eigenstate $\left\vert 0\right\rangle$ of ${\Gamma }_{1}^{B}$ largely gains the Zeeman energy through the magnetization in the hexagonal plane. In contrast, when the field direction is along the c-direction, one of the ${\Gamma }_{6}^{C}$ doublet states, which generates a magnetization parallel to the external magnetic field, becomes the ground state above ~ 1 T and isolates from the other states, considering $\left\vert +7\right\rangle$ of ${\Gamma }_{6}^{C}$ gains a large Zeeman energy. The energy gaps between the ground state and the first excited state for the magnetic field perpendicular and parallel to the c-axis are above 30 K for a magnetic field of 5 T, leading to a large reduction in degeneracy upon the application of the magnetic field. Therefore, the large change in magnetic entropy (ΔS_M = −0.35 J cm⁻³ K⁻¹ (−7.6 J mol⁻¹ K⁻¹)) that was previously reported experimentally⁴ can almost be reproduced by the present mean-field calculation, as shown in Fig. 4c. The magnetization components perpendicular and parallel to the c-aixs are nearly isotropic, and approximately reproduce the experimental value measured with a polycrystalline sample of HoB₂ (Fig. 4d).

The temperature and magnetic field dependences of magnetization, specific heat, and entropy are shown in Supplementary Fig. 2. The results are qualitatively consistent with the experimental data reported in ref. ⁴, except for the double peak behavior in the specific heat observed experimentally at zero field. The peak at T = 15 K, corresponding to the FM phase transition is broadened by the application of a magnetic field, and is concomitant with the peak position largely shifting to higher temperature, which is seen in typical ferromagnets. Conversely, the peak at lower temperature (11 K) shows a completely different behavior; that is, the peak position is not changed by a magnetic field and the sharpness of the peak does not change²¹. Although the origin of the lower phase transition at 11 K has not been understood at the present stage, a previous neutron diffraction study has suggested the possibility of the appearance of quadrupole ordering²¹. Because the quadrupole degree of freedom was not considered in the present mean-field calculation, we did not reproduce the double peak behavior in the specific heat at zero field (Supplementary Fig. 2d). Nevertheless, we observed a sharp peak at H_∣∣c = 1 T (2 T) and T = 10 K (6 K), which corresponded to a spin-reorientation transition from spins parallel to perpendicular to the c-axis. At the present stage, the relationship between the quadrupole ordering and the spin-reorientation transition has not been understood. To further understand the quadrupole ordering, microscopic measurements with a single crystal sample, such as a resonant x-ray scattering, are needed.

Consequently, owing to use of the CEF parameters of HoB₂, a significant decrease in the number of states is possible by the Zeeman splitting along the magnetic fields perpendicular and parallel to the hexagonal c-axis, leading to the large MCE in polycrystalline HoB₂. Therefore, it is necessary to use appropriate CEF level scheme to understand the large MCE in the case of HoB₂. However, we still have a question about ideal CEF level schemes leading to a large MCE at the hydrogen liquefaction temperature in general heavy-rare earth cases.

Crystal electric field level scheme for general heavy rare earth cases

We discuss the ideal CEF level scheme, which gives a theoretical limit for a field change of 5 T, in the general rare-earth cases by mean-field calculations. Experimental investigations have shown that HoN¹⁶ and ErCo₂¹⁴ exhibit a very large ∣ΔS_M∣ (ΔS_M = − 0.29 J cm⁻³ K⁻¹ ( − 5.07 J mol⁻¹ K⁻¹) in HoN and ΔS_M = − 0.37 J cm⁻³ K⁻¹ ( − 10.1 J mol⁻¹ K⁻¹) in ErCo₂). However, the reason for the large difference between the theoretically ideal ΔS_M and experimental values has not been discussed. We attempt to find the ideal CEF level scheme that yields the largest ∣ΔS_M∣ at 20 K for heavy rare-earth ions with a large number of J-multiplets and Tb³⁺(J = 6), Dy³⁺(J = 15/2), Ho³⁺(J = 8), Er³⁺(J = 15/2), and Tm³⁺(J = 6) states. The calculation is based on the self-consistent mean-field method mentioned above. First, we employed cubic point group symmetry, O_h, with two independent CEF parameters, ${B}_{4}^{0}(\equiv {B}_{4})$ and ${B}_{6}^{0}/{k}_{{{{{{{{\rm{B}}}}}}}}}(\equiv {B}_{6})$ (${B}_{4}^{4}=5{B}_{4}^{0}$ and ${B}_{6}^{4}=-21{B}_{6}^{0}$, as described in the Methods section), for all heavy rare-earth ions. Furthermore, we considered the case of hexagonal D_6h symmetry for comparison with HoB₂. In this calculation, we assumed appropriate exchange parameters such that T_C = 20 K.

Figure 5a shows the CEF parameter dependence of ∣ΔS_M∣ when applying a magnetic field of 5 T along the three principal directions at 20 K for Ho³⁺. The ∣ΔS_M∣ value strongly depends on the CEF parameters B₄ and B₆. Note that the parameter set B₄/k_B = B₆/k_B = 0 K, which yields no CEF splitting and has the highest degeneracy of the J-multiplet in the absence of a magnetic field, does not yield the maximum ∣ΔS_M∣ in any cases (Supplementary Table I and Supplementary Fig. 3). Therefore, appropriate CEF parameters sets are needed when designing magnetic refrigeration materials. The maximum value of ∣ΔS_M∣ for Ho³⁺ was found to be approximately − 3 × 10⁻²(K)≤B₄/k_B≤ − 1 × 10⁻²(K) and − 2 × 10⁻⁵(K) ≤ B₆/k_B≤ − 0.5 × 10⁻²(K) K in the field parallel to the [100] direction. The maximum value for Ho³⁺ was $| \Delta {S}_{{{{{{{{\rm{M}}}}}}}}}^{max}| =$12.0 J mol⁻¹ K⁻¹. For the CEF parameters, the ground states were identified to be quasi-6-fold degenerate, wherein one doublet, triplet, and singlet state each in Ho³⁺ were nearly degenerate within the E/k_B = 20 K range (Fig. 5b). Higher-energy excited states are separated from these quasi-ground states by an energy gap larger than 100 K. One of the states in doublet for the quasi-6-fold ground state in zero field exhibits a significant decrease in energy, leading to an isolated ground state in a magnetic field of 5 T with a large energy gap beyond 20 K. For the cases of magnetic fields along the [110] and [111]-directions, we see different ∣ΔS_M∣ map obtained in the calculation. (Fig. 5a) Nevertheless, for the cases along the [110]-direction, the similar set of the CEF parameter gave the maximum ∣ΔS_M∣ = 9.80 J mol⁻¹ K⁻¹, however, the value was substantially lower than that along the [100]-direction.

Fig. 5: Relationship between maximum magnetic entropy change and CEF parameters in heavy rare earth ions around T = 20 K.

a Contour maps of magnetic entropy changes of Ho³⁺ in the cubic O_h symmetry at T = 20 K in magnetic field change from 0 to 5 T along the three principal direction. The powder averaged values are shown in the bottom right figure, b Zeemann splitting in magnetic field along the principal directions at T = 25 K for typical sets of CEF parameters indicated by the star symbols in a, c heavy rare earth ion dependence of the maximum magnetic entropy change for the cubic and hexagonal D_6h symmetries. The experimental value of HoB₂⁴ at 15 K is also plotted. d Zeemann splittings for the case of hexagonal D_6h symmetry at T = 25 K with the CEF parameters that give the maximum magnetic entropy change in Ho³⁺.

The other CEF parameter set, B₄/k_B ~ 0.4 × 10⁻² K and B₆/k_B ~ − 2 × 10⁻⁵ K yielded the maximum ∣ΔS_M∣ for the magnetic field parallel to the [111] direction, and the ground state was quasi-8-fold degenerate, with one doublet and two triplets in Ho³⁺. On applying a magnetic field of 5 T along the [111] direction, the energy of the doublet state significantly decreased, leading to an isolated ground state. For the other heavy rare-earth cases, Tb³⁺, Dy³⁺, Er³⁺, and Tm³⁺, we calculated the ∣ΔS_M∣ values and the Zeeman splitting, as shown in Supplementary Figs. 2 and 3. Consequently, we found that the ideal set of CEF and exchange parameters in heavy rare-earth ions yields ∣ΔS_M∣ ~ 12 J mol⁻¹ K⁻¹ in the single-crystal case for Dy³⁺, Ho³⁺, and Er³⁺ and ∣ΔS_M∣ ~ 7 J mol⁻¹ K⁻¹ in the cubic O_h case for Tb³⁺, and Tm³⁺ (Fig. 5c). The maximum ∣ΔS_M∣ value and the corresponding CEF parameters for the rare-earth ions are listed in Supplementary Table I. The corresponding Zeeman splittings are also illustrated in Supplementary Figs. 4 and 5.

From the practical application perspective for magnetic refrigeration cooling, polycrystalline particles could be used as the magnetic refrigeration materials²², because of the kg order of magnetic refrigeration material particles required for the AMR system, which is allowed only for polycrystalline samples. Therefore, powder-averaged ∣ΔS_M∣ values are more important in the practical case. The maximum values of ∣ΔS_M∣ in the polycrystalline case were estimated to be 8.15 J mol⁻¹ K⁻¹ for Dy³⁺, 8.51 J mol⁻¹ K⁻¹ for Ho³⁺, and 7.88 J mol⁻¹ K⁻¹ for Er³⁺ in B₄/k_B ~ − 2.4 × 10⁻² K and B₆/k_B ~ − 2.0 × 10⁻⁵ K in the cubic case, as can be seen in Fig. 5a, c as well as Supplementary Fig. 2.

The experimental values obtained using typical cubic systems are compared with the theoretical values obtained from the present calculations. Because the ∣ΔS_M∣ value generally shows significant T_C dependence^23,24,25, we calculated the T_C dependences of the ideal set of the CEF parameters and the maximum ∣ΔS_M∣ values for the cubic O_h case to compare the theoretical and experimental values. As the calculated results are summarized in Supplementary Figs. 6–10, the maximum ∣ΔS_M∣ significantly depends on T_C (Supplementary Fig. 6), whereas the ∣ΔS_M∣ maps as functions of CEF parameters almost similar for the temperature region from 15 K to 80 K (Supplementary Figs. 7–10). ErAl₂ has a significantly large ∣ΔS_M∣ value of ~ 8.8 J mol⁻¹ K⁻¹ at 14 K in polycrystalline sample¹³, which is almost consistent with the theoretical value obtained in the present calculation (Supplementary Fig. 6a). By comparing the previously reported CEF parameters in the O_h symmetry of ErAl₂¹¹, to the present calculation at T_C = 15 K (Supplementary Fig. 7a), we found that the set of CEF parameters, B₄/k_B = 1.3 × 10⁻³ K and B₆/k_B = − 1.6 × 10⁻⁵ K, in ErAl₂ is close to the ideal one. On the other hand, the ∣ΔS_M∣ value of HoAl₂ was ~ 5.5 J mol⁻¹ K⁻¹ at 30 K¹³. This value is much lower than the maximum value for Ho³⁺, ~ 8.5 J mol⁻¹ K⁻¹ (Supplementary Fig. 6b), which is because the CEF parameter set (B₄/k_B = − 9.9 × 10⁻⁴ K and B₆/k_B = 8.2 × 10⁻⁶K¹¹) in HoAl₂ differs significantly from the ideal one. By contrast, the ∣ΔS_M∣ value of ErCo₂ (10.1 J mol⁻¹K⁻¹ at 36 K¹⁴) is significantly larger than the theoretical limit, which can be due to the additional entropy contributions of Co moments and the different nature of the phase transition (first-order transition in ErCo₂)^5,14.

For comparing the experimental values for the polycrystalline HoB₂ (∣ΔS_M∣ = 0.35 J cm⁻³ K⁻¹ (7.6 J mol⁻¹ K⁻¹)) with the theoretical values, we calculated the ideal value in hexagonal symmetry (D_6h). The maximum values for the single-crystal case with the magnetic field perpendicular and parallel to the hexagonal c-axis are 10.3 J mol⁻¹ K⁻¹ and 11.5 J mol⁻¹ K⁻¹, respectively (Fig. 5c). When the field is perpendicular to the c-axis, the ∣ΔS_M∣ is the maximum for ${B}_{2}^{0}/{k}_{{{{{{{{\rm{B}}}}}}}}}$= 0.02 K, ${B}_{4}^{0}/{k}_{{{{{{{{\rm{B}}}}}}}}}$ = −0.001 K, and ${B}_{6}^{0}/{k}_{{{{{{{{\rm{B}}}}}}}}}=0.3\times 1{0}^{-5}$ K, ${B}_{6}^{6}/{k}_{{{{{{{{\rm{B}}}}}}}}}=0.6\times 1{0}^{-4}$ K, leading to a quasi-10-fold degenerate ground state (left figure of Fig. 5d). When the field is parallel to the c-axis, the maximum ∣ΔS_M∣ was found in ${B}_{2}^{0}/{k}_{{{{{{{{\rm{B}}}}}}}}}$=0.08 K, ${B}_{4}^{0}/{k}_{{{{{{{{\rm{B}}}}}}}}}$ = −0.001 K, ${B}_{6}^{0}/{k}_{{{{{{{{\rm{B}}}}}}}}}=-0.9\times 1{0}^{-5}$ K, $| {B}_{6}^{6}/{k}_{{{{{{{{\rm{B}}}}}}}}}| < 0.1\times 1{0}^{-4}$ K, which makes the ground state quasi-11-fold degenerate (right figure of Fig. 5d). By comparing the ideal CEF level scheme with the experimental one with a quasi-quintuple ground state in HoB₂, the degree of degeneracy in the case of zero field in HoB₂ is doubly lower than that of the theoretically ideal case. The ideal powder-averaged maximum value of 10.1 J mol⁻¹ K⁻¹ at ${B}_{2}^{0}/{k}_{{{{{{{{\rm{B}}}}}}}}}$=0.03 K, ${B}_{4}^{0}/{k}_{{{{{{{{\rm{B}}}}}}}}}$ = −0.001 K, ${B}_{6}^{0}/{k}_{{{{{{{{\rm{B}}}}}}}}}=-0.2\times 1{0}^{-5}$ K, ${B}_{6}^{6}/{k}_{{{{{{{{\rm{B}}}}}}}}}=-0.6\times 1{0}^{-4}$ K) in Ho³⁺ with a hexagonal symmetry is 33% larger than that of HoB₂ (7.6 J mol⁻¹ K⁻¹) (Fig. 5c). Therefore, there is scope for enhancing the value of ∣ΔS_M∣ even in HoB₂, which is a well-known material with a large MCE.

We provided the theoretical limits of ∣ΔS_M∣ with a magnetic field change of 5 T in heavy rare-earth systems within the mean-field approximation by searching the ideal CEF parameter sets for cubic (O_h) and hexagonal (D_6h) symmetries. Recent advancements in density functional theory calculations have unlocked the possibility of predicting CEF parameters for rare-earth systems based on the crystal information^26,27,28. As a result, a combination of DFT calculations and the relationships between ∣ΔS_M∣ and the CEF parameters derived in this study would accelerate the search for compounds with a large MCE and design more magnetic refrigeration materials.

Conclusions

In summary, because of the growing demand for liquefied hydrogen as an energy storage medium, research on magnetic refrigeration materials that can be used in the temperature range of several tens of kelvins has attracted wide attention. This study investigated the relationship between the CEF level scheme and the large MCE in the hydrogen liquefaction temperature range for general heavy rare-earth compounds, as well as the special case of HoB₂. Using inelastic neutron scattering spectroscopy, we identified the CEF level scheme in HoB₂ that reproduces the large MCE. Furthermore, we identified the ideal CEF parameters and energy level schemes that yield the maximum ΔS_M for general heavy rare-earth systems using the mean-field approximation with the exchange interactions and CEF. The ideal CEF level schemes yielded highly degenerate ground states in a zero magnetic field and a potentially isolated singlet state in a finite magnetic field. A comparison of the values obtained from the ideal CEF level schemes with the experimental values indicated scope for further investigation. We believe the relationships between ΔS_M and CEF parameters derived in this study can provide additional guidelines for searching compounds with a large MCE and for further investigation on magnetic refrigeration materials.

Methods

Sample preparation

A polycrystalline sample of HoB₂ was synthesized by an arc-melting process in a water-cooled copper hearth arc furnace. Stoichiometric amounts of Ho (99.9% purity) and the ¹¹B enriched isotope (99.5%) were melted in an argon atmosphere. The as-cast sample vacuum sealed in a quartz tube was heat treated at 1000 °C for 7 days for homogenization and quenched in water. To determine the sample quality, we used the powder x-ray diffraction technique. We confirmed that the main phase was HoB₂ for the heat-treated sample. A small amount of the impurity phase Ho₂O₃ was detected, with the volume fractions being less than 8%.

Inelastic neutron scattering experiment

The scattering intensity observed in the INS experiment was proportional to the transition intensity of the total angular momentum operator (Eq. (4)). Therefore, we could directly observe the CEF Hamiltonian, including the momentum operator (Eq. (1)) as follows²⁹:

$$\frac{{d}^{2}\sigma }{d\Omega d\epsilon }=N{\left(\frac{\gamma {r}_{0}}{2}\right)}^{2}\frac{{k}_{f}}{{k}_{i}}\exp [-2W]\,{f}^{2}({{{{{{{\boldsymbol{\kappa }}}}}}}})\mathop{\sum }\limits_{n,m}{\rho }_{n}(T)| \langle m| {J}_{\perp }| n\rangle {| }^{2}\delta ({E}_{n,m}-\epsilon )$$

(4)

where γ is the magnetic moment of the neutron, r₀ is the classical electron radius, $\exp [-2W]$ is the Debye-Waller factor, f(κ) is the magnetic form factor of the rare earth ion, J_⊥ is the component of the total angular momentum perpendicular to the scattering vector κ expressed as κ = k_f − k_i with the incident (final) momentum k_i(f), ρ_n(T) is the Boltzmann population of the state $\left\vert n\right\rangle$, and E_n,m is the transition energies between the CEF states $\left\vert m\right\rangle$ and $\left\vert n\right\rangle$ belonging to the ground state J-multiplet. In the present fitting procedure, the δ-function in Eq. (4) was substituted by a Lorentz type spectral function (Eq. (5)) in the fitting procedure.

$$P(\epsilon )=\frac{1}{2\pi }\left\{\frac{\zeta }{{(\epsilon -{\epsilon }_{0})}^{2}+{\zeta }^{2}}+\frac{\zeta }{{(\epsilon +{\epsilon }_{0})}^{2}+{\zeta }^{2}}\right\},$$

(5)

where ζ is the width of spectrum at the energy position at ϵ₀.

INS experiments were performed using the enriched powder sample Ho¹¹B₂ and High resolution chopper spectrometer (HRC) installed at BL12 in J-PARC MFL, Tokai, Japan. To measure the INS spectra for a wide energy range with high energy resolution, we selected multiple incident neutron energies, ϵ_i = 10.16 meV, 39.97 meV, and 102.3 meV, where the energy resolution widths at the elastic conditions were 0.2 meV, 1.1 meV, and 2.48 meV, respectively. The powder sample was packed into an aluminum foil sample holder with a thin plate shape of the dimensions 20 x 20 x 2.0, which was enclosed into an aluminum cell with thermal exchange He gas. The sample mass was 6.3 g. We used a standard closed-cycle He gas refrigerator to cool the sample to 4 K. To eliminate the background contribution in the measured spectra, we measured the empty aluminum holder and the cell in the same temperature range. The experimental spectra shown in Figs. 2 and 3 were the data after subtracting the background. Moreover, we measured polycrystalline Ho₂O₃ with the same setup and temperature conditions to demonstrate how a small amount of impurity phase affects the INS spectra of HoB₂. Lastly, we confirmed that no significant contribution from Ho₂O₃ was detected.

Mean-field calculation

The mean-field Hamiltonian that includes the CEF term with either cubic O_h¹¹ or hexagonal D_6h¹⁷ point ground symmetry, and the magnetic term ${{{{{{{{\mathcal{H}}}}}}}}}_{{{{{{{{\rm{mag}}}}}}}}}$, is expressed as:

$${{{{{{{{\mathcal{H}}}}}}}}}_{{{{{{{{\rm{total}}}}}}}}}={{{{{{{{\mathcal{H}}}}}}}}}_{{{{{{{{\rm{CEF}}}}}}}}}+{{{{{{{{\mathcal{H}}}}}}}}}_{{{{{{{{\rm{mag}}}}}}}}},$$

(6)

$${{{{{{{{\mathcal{H}}}}}}}}}_{{{{{{{{\rm{CEF}}}}}}}}}({O}_{h})={B}_{4}\left({O}_{4}^{0}+5{O}_{4}^{4}\right)+{B}_{6}({O}_{6}^{0}-21{O}_{6}^{4}),$$

(7)

$${{{{{{{{\mathcal{H}}}}}}}}}_{{{{{{{{\rm{CEF}}}}}}}}}({D}_{6h})={B}_{2}^{0}{O}_{2}^{0}+{B}_{4}^{0}{O}_{4}^{0}+{B}_{6}^{0}{O}_{6}^{0}+{B}_{6}^{6}{O}_{6}^{6},$$

(8)

$${{{{{{{{\mathcal{H}}}}}}}}}_{{{{{{{{\rm{mag}}}}}}}}}=-g{\mu }_{B}({\mu }_{0}{{{{{{{\boldsymbol{H}}}}}}}}+\lambda g{\mu }_{B}\langle {{{{{{{\boldsymbol{J}}}}}}}}\rangle )\cdot {{{{{{{\boldsymbol{J}}}}}}}}$$

(9)

where the coefficients ${B}_{l}^{m}$ are the CEF parameters and the ${O}_{l}^{m}$ are Steven’s operator equivalents. g, μ_B, H, and J are the Landé g-factor, Bohr magneton, external magnetic field, and total angular momentum operator, respectively. By a standard diagonalization technique, eigenvalues and eigenstates can be obtained as E_i and φ_i. Using E_i and φ_i, the thermal average of the total angular momentum, expressed as:

$$\langle {{{{{{{\boldsymbol{J}}}}}}}}\rangle =\mathop{\sum }\limits_{i}^{2J+1}[{\varphi }_{i}^{* }{{{{{{{\boldsymbol{J}}}}}}}}{\varphi }_{i}]{e}^{-{E}_{i}/{k}_{{{{{{{{\rm{B}}}}}}}}}T}/Z,$$

(10)

with the partition function

$$Z=\mathop{\sum }\limits_{i}^{2J+1}{e}^{-{E}_{i}/{k}_{{{{{{{{\rm{B}}}}}}}}}T}{e}^{\lambda {g}^{2}{\mu }_{B}^{2}{\langle {{{{{{{\boldsymbol{J}}}}}}}}\rangle }^{2}/2{k}_{{{{{{{{\rm{B}}}}}}}}}T},$$

(11)

was calculated so that 〈J〉 is self-consistently determined. With the determined 〈J〉 and Z, we calculated the free energy $F=-{k}_{{{{{{{{\rm{B}}}}}}}}}T\,{{{{{{{\rm{\ln }}}}}}}}(Z)$, and the physical quantities, based on the definitions of magnetization (〈M〉), specific heat(C) and entropy (S).

$$\langle {{{{{{{\boldsymbol{M}}}}}}}}\rangle =-g{\mu }_{B}\langle {{{{{{{\boldsymbol{J}}}}}}}}\rangle ,$$

(12)

$$S=-\left(\frac{\partial F}{\partial T}\right),$$

(13)

$$C=T\left(\frac{\partial S}{\partial T}\right).$$

(14)