Introduction

The rational design of architected materials with anisotropic properties enables them to offer optimal, multi-functional performance. For example, nature uses evolutionarily optimized micro-architectures to combine extremely high stiffness (in selected directions) with a light weight (e.g., in wood and bone1,2,3) or to combine ultrahigh stiffness values with ultrahigh toughness (e.g., in nacre4,5,6). In man-made designer materials that are also known as metamaterials, other combinations of mechanical properties may be sought, as they allow for devising novel functionalities. For example, a combination of auxetic behavior in various orthogonal directions and high stiffness is instrumental for the structural applications of auxetic materials7,8,9.

To achieve a desired combination of material properties, the primary challenge is to find the specific micro-architectures that give rise to the desired properties. Once the micro-architecture is determined, the metamaterial can be fabricated using additive manufacturing (=3D printing) techniques. The recent emergence of powerful multi-material 3D printing techniques means that the micro-architecture not only consists of rationally designed, complex geometries but can also combine multiple materials with different mechanical properties. Many other design features found in nature, such as hierarchical micro-architectures10,11,12,13, functional gradients (in terms of both geometries and material properties)14,15, and soft–hard composites (similar to the organic and mineral phases in bone11,16,17) can be also realized to expand the range of the achievable properties.

Given such a wide range of possibilities for the fabrication of metamaterials with complex (multi-scale) geometries and complex spatial distributions of material properties, the space of possible design parameters is formidably large. Optimizing the design parameters is, therefore, challenging and requires an excessively large number of computational models to be solved. Such simulations are required not only to understand how the design parameters relate to the anisotropic elastic properties but, more importantly, to discover the very rare designs that give rise to the desired properties. For example, double-auxeticity (i.e., auxetic properties in two orthogonal directions) is very rare (i.e., as little as <1.6% of the possible designs) in two-dimensional lattices18. Combining the double-auxeticity with the additional requirement of possessing high stiffness values in (both) directions results in the excessive rarity of micro-architectures that satisfy the design requirements.

Computational models, therefore, need to scan a vast design space to find rare events. Due to the “curse of dimensionality”19, the number of designs that need to be evaluated is so large (≈7.7 × 1043, see Supplementary Table 1) that extremely fast models and highly parallelizable algorithms are required. Computational models, such as finite element (FE) models, are not fast enough for that purpose. Here, we used deep learning to establish a mapping from the space of design parameters to that of the anisotropic elastic properties, thereby decreasing the solution time to ≈2.4 × 10−6 s while also making the evaluation process extremely parallelizable. Recent progress in machine learning has led to significant achievements in different scientific fields20, including the design of composites and metamaterials21,22,23,24,25,26,27,28 prediction of material properties29,30,31, the prediction of elasticity distributions to circumvent the inverse problem of elasticity imaging32,33, and optimization of manufacturing processes34,35. However, the advantages of such artificial intelligence approaches have not yet been demonstrated in the case of designing multi-material mechanical metamaterials to achieve very rare target properties.

The main objective of the present research was to use computational models and deep learning models to predict the mechanical properties of multi-material mechanical metamaterials, allowing us to discover very rare designs that exhibit highly desirable combinations of elastic properties (e.g., high stiffness and highly negative Poisson’s ratio). We used planar lattices based on the re-entrant, cubic, and honeycomb unit cells (corresponding to the cell angles of \({60}{^\circ }\), \({90}{^\circ }\), and \({120}{^\circ }\), respectively) with random distributions of hard and soft phases. The ratio of the hard phase volume to the soft phase volume was varied as well (i.e., \({{\rho }}_{{{{{{\rm{h}}}}}}}\left({ \% }\right) ={5}{,}\,{10}{,}\,{20}{,}\,{30}{,}\,{40}{,}\,{50}{,}\,{60}{,}\,{70}{,}\,{80}{,}\,{90}\), and \({95}\)). FE models were then created to generate the training dataset required for the training of a deep learning model (i.e., the single unit cell model). Moreover, we selected three designs (one from each unit cell angles of \({60}{^\circ }\), \({90}{^\circ }\), and \({120}{^\circ }\)) to be fabricated using an advanced multi-material 3D printing technique and applied digital image correlation (DIC) to measure the full-field strain patterns during the mechanical testing of the fabricated specimens. After training, the deep learning model was used to predict the elastic properties of a wide range of lattices (1.5 × 109 different designs), given their design parameters. We also studied various combination of tiled designs (e.g., four-tile and nine-tile structures) to show how combining multiple instances of these random lattices into a hybrid, tiled lattice can boost the possible range of mechanical properties. We also trained another deep learning model (i.e., the four-tile model) which predicts the mechanical properties resulting from the various combinations of four tiles with different mechanical properties. A fabrication and mechanical testing procedure similar to the one mentioned above (but without DIC) was applied to experimentally characterize seven additional tiled designs (i.e., four four-tile structures and three nine-tile structures).

Results

Training and performance of the deep learning models

Using a Workstation (CPU = Intel® Core™ i9-8950HK, RAM = 32.0 GB) and one running script, each FE simulation could be performed between 6.2 × 10−2 ± 2.7 × 10−3 and 6.5 × 10−3 ± 8.2 × 10−4 s while each deep learning prediction took between 8.3 × 10−2 ± 2.9 × 10−3 and 1.2 × 10−5 ± 1.2 × 10−6 s depending on the number of simultaneously run simulations/predictions (a comparison between the FE simulation time and the deep learning prediction time for the single unit cell model is presented in Supplementary Fig. 1). The solution time per design also depends on the number of scripts run in parallel. For instance, for 105 simultaneously run simulations and 106 simultaneously run deep learning predictions, each FE simulation could be performed between 5.0 × 10−3 ± 4.9 × 10−4 and 2.5 × 10−3 ± 1.3 × 10−4 s while each deep learning prediction took between 1.3 × 10−5 ± 1.8 × 10−7 and 2.4 × 10−6 ± 1.2 × 10−7 s depending on the number of simultaneously run scripts.

Within 200 epochs of training, the prediction errors (the mean absolute error (MAE) as well as the mean squared error (MSE)) of the single unit cell models reduced from 6.6 × 10−4 and 1.38 × 10−2 to 1.05 × 10−4 and 6 × 10−3, respectively. Meanwhile, the prediction errors (MSE and MAE) of the validation dataset decreased from 4.25 × 10−4 and 1.19 × 10−2 to 1.14 × 10−4 and 6.38 × 10−3, respectively. In the case of the four-tile model, the prediction errors (MSE and MAE) corresponding to the training and validation datasets reduced within 200 epochs from (MSE = 3.1 × 10−4, MAE = 1.24 × 10−2) and (MSE = 1.88 × 10−4, MAE = 1.02 × 10−2) to (MSE = 3.27 × 10−5, MAE = 4.3 × 10−3) and (MSE = 3.68 × 10−5, MAE = 4.6 × 10−3). The coefficient of determination of both single unit cell and four-tile deep learning models was 9.98 × 10−1 (Supplementary Table 2), indicating that these models were highly accurate in predicting the mechanical properties of both types of soft–hard lattices. Given this high degree of accuracy, the deep learning models were used in the rest of the study for evaluating the mechanical properties of the designed structures.

Single unit cell deep learning model

We used the trained ‘single unit cell’ deep learning model to predict the mechanical properties of 1.5 × 109 random structures. The predicted ranges of the elastic moduli (i.e., \({E}_{11}\in 0\,{{{{{\rm{to}}}}}}\,10.94\) and \({E}_{22}\in 0\,{{{{{\rm{to}}}}}}\,0.55\,{{{{{\rm{MPa}}}}}}\)) and Poisson’s ratios (i.e., \({\nu }_{12}\in -1.24\,{{{{{\rm{to}}}}}}\,1.16\) and \({\nu }_{21}\in -0.53\,{{{{{\rm{to}}}}}}\,0.51\)) were quite broad (more information is provided in Supplementary Table 3 for the specific subset of data presented in Fig. 1). Along direction 1, a wide range of elastic properties (i.e., \({E}_{11}\), \({\nu }_{12}\) duos) were obtained within a conifer cone-like region. In comparison, the range of the elastic properties found for direction 2 (i.e., \({E}_{22}\), \({\nu }_{21}\) duos) was narrower and included several bean-like regions (Fig. 1a). High elastic modulus (\({E}_{11}\)) values were achieved when orthogonal unit cells were used, which is expected, given that the deformation of orthogonal unit cells under orthogonal loading is primarily stretch dominated. Highly negative and highly positive Poison’s ratios were predicted for the lattices based on the re-entrant and honeycomb unit cells, respectively. \({E}_{11}\) and the absolute value of \({\nu }_{12}\) were inversely correlated for \({\rho }_{{{\rm {h}}}}\) values up to 80%, after which they were directly correlated (Fig. 1a). According to the predictions of the Hashin–Shtrikman theory and the theoretical limits established for composite materials36,37, an inverse relationship between the elastic modulus and Poisson’s ratio is expected. However, the direct correlation observed for the \({\rho }_{{\rm {h}}}\) values exceeding 80% is caused by the non-affinity imposed by the random distribution of the hard phase within the lattice structures. In another study38, we showed that the Poisson’s ratio and the degree of non-affinity (\(\varGamma\)) are related to each other through a power law for both re-entrant and honeycomb unit cells. Furthermore, it was concluded that regardless of the type of the unit cell and the level of the applied strain, the degree of non-affinity increases with \({\rho }_{{{\rm {h}}}}\) until a maximum value is reached at \({\rho }_{{\rm {h}}}\) = 75–90% after which it decreases to reach \(\varGamma =0\) for the structures only made from the hard phase (i.e., \({\rho }_{{\rm {h}}}=100 \%\)). These statements clearly explain the asymmetry in the plot of \({E}_{11}\) vs. \({\nu }_{12}\) for both re-entrant and honeycomb types of the unit cells.

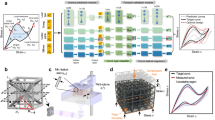
Fig. 1: The structures of the optimized deep learning models as well as relevant training procedures and the range of attainable mechanical properties.
figure 1

We trained two optimized deep learning models, namely single unit cell model (a) and four-tile model (b) for designing multi-material lattice structures. The strain distribution and deformation patterns obtained from FEM and DIC for selected representative designs are presented in (a). The prediction vs. simulation results and the coefficients of determination for the test datasets are, respectively, presented in Supplementary Fig. 2a and b for the single unit cell and four-tile models. Given the very large number of data points which makes the generation of the plots challenging, only the data points for which the FE models were directly solved (i.e., 1% of the data points) are plotted in Fig. 1.

Full size image

Four-tile deep learning model

Using the four-tile deep learning model, we studied the elastic properties resulting from the various combinations of four tiles with different mechanical properties (Fig. 1b). Along direction 1, the region representing the attainable properties is less symmetric (Fig. 1b) but is nevertheless more so than the one achieved with a single unit cell model (Fig. 1a). Along direction 2, the range of properties corresponding to the four-tile model covered a near-square region, which is a remarkable achievement and means that high values of elastic modulus can be combined with highly negative or highly positive values of the Poisson’s ratio (Fig. 1b). These observations confirm that a simple four-tile arrangement of the random multi-material designs can greatly expand the achievable range of anisotropic elastic properties.

Role of multi-material design

In the single unit cell model, the ranges of both elastic moduli (E11, E22) monotonically increased with \({\rho }_{{\rm {h}}}\) regardless of the type of unit cell (Fig. 2a). This is expected, given that increasing the volume ratio of the hard phase to the soft phase simply increases the elastic modulus of the composite lattice structure. The plots of the Poisson’s ratios vs. \({\rho }_{{\rm {h}}}\) were not monotonic with the absolute values of \(\nu\) initially increasing until a global extremum was reached for \({\rho }_{{\rm {h}}} \, > \, 50 \%\) (i.e., 60–80%), followed by a decreasing trend. For all the three types of unit cells, the ranges of the attainable Poisson’s ratios were the widest for \({\rho }_{{\rm {h}}}=60\!-\!80 \%\). This is the range where the multi-material nature of the designs plays the most important role in determining the Poisson’s ratio of the lattice structure, given that both phases have comparable effects. For smaller or larger values of \({\rho }_{{\rm {h}}}\), either the soft or the hard phase dominates the mechanical response of the lattice structure, respectively. For a fixed value of the Poisson’s ratio (i.e., \({\nu }_{12}=-1\pm 0.01,{\nu }_{12}=0\pm 0.01\), and \({\nu }_{12}=1\pm 0.01\)), a wide range of elastic moduli were achieved, depending on the type of unit cell and \({\rho }_{{\rm {h}}}\) (Fig. 2b). For fixed values of \(\nu\) and \({\rho }_{{\rm {h}}}\), the largest range of the elastic moduli was achieved for the larger \({\rho }_{{\rm {h}}}\). For example, for the designs with orthogonal unit cells and with a \({\rho }_{{\rm {h}}}\) value of 80%, the elastic modulus can change by up to 10.7 folds, depending on how the hard and soft phases are assigned to the lattice structure and without any noticeable change in the Poisson’s ratio (i.e., \(\,{\nu }_{12}=0\pm 0.01\)). This highlights the importance of multi-material design aspect in the tunability of the elastic properties of mechanical metamaterials.

Fig. 2: The elastic properties of studied lattice structures with a focus on double-auxetic lattices.
figure 2

a The elastic properties (\({E}_{11},{\nu }_{12},{E}_{22},\) and \({\nu }_{21}\)) of the different types of unit cells for the different values of \({\rho }_{{\rm {h}}}\). b The achievable range of the elastic moduli for some specific values of the Poisson’s ratio (i.e., \({\nu }_{12}=-1\pm 0.01,{\nu }_{12}=0\pm 0.01\), and \({\nu }_{12}=1\pm 0.01\)) considering the different values of \({\rho }_{{\rm {h}}}\). c The elastic properties corresponding to the single unit cell and four-tile designs with a focus on double-auxetic lattices. The magnified view shows the distribution of double-auxetic structures by types of unit cells of constituent designs. Given the very large number of data points which makes the generation of the plots challenging, only the data points for which the FE models were directly solved (i.e., 1% of the data points) are plotted in Fig. 2.

Full size image

Stiff double-auxetic structures

We also studied how the assignment of hard and soft phases in multi-material lattices as well as combining different types of unit cells in a four-tile structure could be used to achieve double-auxetic, yet stiff structures. When combining different types of unit cells, one of the chosen unit cell types should always be the re-entrant unit cell, leading to four possible combinations. To study the probability of finding double-auxetic structures with high stiffness values, we defined a characteristic number (i.e., \(\alpha ={\bar{E}}_{1}\times {\bar{E}}_{2}\times {\bar{\nu }}_{12}\times {\bar{\nu }}_{21}\)) that sums up the effects of both the Poisson’s ratios and stiffness in a single number. The overline refers to the fact that all the properties (i.e., \({E}_{1}\), \({E}_{2}\), \({\nu }_{12}\), and \({\nu }_{21}\)) were normalized between 0 and 1. We calculated \(\alpha\) for all the double-auxetic single unit cell and four-tile model structures (Supplementary Table 4 and Supplementary Fig. 3). Among all the single unit cell and four-tile lattice structures plotted in Fig. 1, 0.08% and 0.58% (respectively), had \(\alpha\) values that were 5 standard deviations higher than their corresponding mean values. Furthermore, the results indicated that a four-tile combination of unit cells enables us to achieve double-auxetic, yet stiff lattice structures (Fig. 2c). Double-auxeticity is a rare event on its own18, let alone combined with high stiffness, further underscoring the importance of the implemented design strategies. Furthermore, the presented combinations of different unit cell types enable a better coverage of the \(({E}_{11},\,{E}_{22})\) and \(({\nu }_{12},{\nu }_{21})\) planes.

Tiled and transformed structures

We selected the following single unit cells designs for a more in-depth study: a design with the highest values of \({E}_{11}\) and \({E}_{22}\) from the orthogonal unit cell group (\({E}_{11}=9.67\), \({E}_{22}=0.31{{{{{\rm{MPa}}}}}}\), \({\nu }_{12}=-0.04\), and \({\nu }_{21}=0.00\)), a design with the most negative value of the Poisson’s ratio and almost the highest elastic modulus from the re-entrant unit cell group (\({E}_{11}=0.93\), \({E}_{22}=0.26{{{{{\rm{MPa}}}}}}\), \({\nu }_{12}=-1.17\), and \({\nu }_{21}=-0.45\)), and a design with the most positive value of Poisson’s ratio and an almost highest elastic modulus from the honeycomb unit cell group (\({E}_{11}=1.31\), \({E}_{22}=0.52{{{{{\rm{MPa}}}}}}\), \({\nu }_{12}=1.05\), and \({\nu }_{21}=0.47\)). We then arranged these designs into four-tile (Fig. 3a) and nine-tile (Fig. 3b) structures and obtained their mechanical properties and deformation patterns both computationally and experimentally. Moreover, we studied how a 90° rotation of a design would affect the mechanical properties of the combined structures (Fig. 3a). We found that combining the abovementioned designs further expanded the space of achievable elastic properties, filling the gaps in mechanical properties of individual unit cells. For instance, in structure 1 (Fig. 3a) and structure 5 (Fig. 3b), the combination of re-entrant and orthogonal unit cells boosted the elastic modulus (\({E}_{11}\)) of the constituent re-entrant unit cell by 75.6% and 91.4%, respectively, while the Poisson’s ratio maintained its extreme negative values (\({|\nu }_{12}|\) reduced by 6.6% and 9.4%, respectively). In structure 2 (Fig. 3a) and structure 6 (Fig. 3b), the combination of honeycomb and orthogonal unit cells boosted the elastic modulus (\({E}_{11}\)) of the constituent honeycomb unit cell by 40% and 40.4%, respectively, while the extreme positive Poisson’s ratios did not change much (\({|\nu }_{12}|\) reduced only by 1.4% and 2.8%, respectively).

Fig. 3: Different combinations of designs with extreme mechanical properties.
figure 3

These designs are selected from each group of the unit cells (i.e., a re-entrant structure with a highly negative Poisson’s ratio, a honeycomb structure with a highly positive Poisson’s ratio, and an orthogonal structure with a high value of the elastic modulus). a The mechanical properties of two four-tile structures with non-rotated and rotated tiles and the distribution of the von Mises stresses in these lattice structures. These multi-material 3D printed specimens were mechanically tested in both the 1- and 2-directions under 3% tensile strain and the experimental results were compared with the FE simulation results (Table 1). b The mechanical properties of nine-tile combinations and the von Mises stress distribution in these combinations. These multi-material 3D printed specimens were mechanically tested in both the 1- and 2-directions under 3% tensile strain, and the experimental results were compared with the FE simulation results (Table 1).

Full size image

We also showed that with a 90° rotation of a design, we could increase the elastic modulus in the weak direction (\({E}_{22}\)) and create structures with a higher level of isotropy. In this way, we could achieve structures with a higher elastic modulus (\({E}_{22}\)) than both types of their constituent designs. For example, the elastic modulus (\({E}_{22}\)) of structure 3 was 56.2% and 31% higher than the elastic modulus (\({E}_{22}\)) of the constituent re-entrant and orthogonal unit cells, respectively (Fig. 3a). In structure 4 (Fig. 3a), the elastic modulus (\({E}_{22}\)) was 4.5% and 75.3% higher than the elastic modulus (\({E}_{22}\)) of the constituent honeycomb and orthogonal unit cells, respectively.

We also showed how the change of boundary conditions would affect the deformation patterns and also contributed to a more uniform stress distribution within the lattice structure. In all designs, the experimental observations regarding the deformation patterns as well as the experimental values of the mechanical properties clearly agreed with our computational results (Table 1), confirming the validity of the computational approach used here.

Table 1 Comparisons between the computationally determined and experimentally measured elastic properties of the multi-tile designs.
Full size table

Furthermore, the combination of structures with different types of unit cells allows for different functionalities. For instance, the hybrid combination of negative Poisson’s ratios with positive values could be used to design orthopedic implants with improved longevity39. Combining different types of unit cells could create action-at-a-distance behavior that enables different patterns of local actuation using a single far-field deformation and has various potential applications in soft robotics40. Here, we also showed that combining different unit cells allows for shape-morphing boundaries as well as for specific values of the Poisson’s ratio. For instance, different shape-morphing boundaries were observed in structure 7 (Fig. 3b) when re-entrant and honeycomb unit cells were combined with each other, while the designed structure had a zero value of the Poisson’s ratio in both directions. Such properties are of high interest in high added value industries, such as the biomedical and aeronautical industries, as they exhibit improved damping performance41.

Uniformity of stress distribution

To date, most studies on mechanical metamaterials have focused on the elastic properties of architected lattices without paying much attention to the structural integrity aspects including the risk of failure due to such phenomena as stress concentrations. Generally speaking, the presence of stress concentration leads to premature failure caused by premature initiation and growth of cracks. It is, therefore, desirable to distribute the stresses as uniformly as possible within the lattice structure. An important advantage of having giga-sized databases of possible designs with the corresponding elastic properties is the possibility to apply additional design criteria, such as the one related to the uniformity of the stress distribution.

For example, among all the single unit cell designs with the same range of elastic properties (i.e., \(0.15 \, < \, {E}_{11} \,[MPa] \, < \, 0.25,{-1.1} \, < \, {\nu}_{12} \, < \,{-1}, 0.01 \, < \, {E}_{22} \, [MPa] \, < \, 0.08,\) and \(-0.45 \, < \, {\nu }_{21} \, < \, {-0.3}\)), we studied the uniformity of the stress distributions within the lattice structure. In total, 207 tiles with various \({\rho }_{{\rm {h}}}\) values (i.e., \(50\%,\,60\%,\,70\%,\,{{\rm {and}}}\,80 \%\)) were included (Fig. 4a). The maximum values of the von Mises stress in the structural elements of these designs were calculated while these designs were subjected to two different boundary conditions (i.e., \({\varepsilon }_{11}=3 \%\) or \({\varepsilon }_{22}=3 \%\)) (Fig. 4b). Although the elastic properties of these designs were generally very similar, the maximum von Mises stresses in their struts varied up to 2.5 and 6.5 times along the loading conditions 1 and 2, respectively. This finding indicates the importance of applying an additional design rule regarding the stress uniformity within the structure. For that reason, two designs with \({\rho }_{{\rm {h}}}=70 \%\) (one with the minimum and one with the maximum Euclidean distance from the origin) were selected for a more in-depth analysis (Fig. 4b and c). A closer study of the stress distributions in these two structures showed a clear incident of stress concentration in design 2 while design 1 exhibited more uniform stress distributions (Fig. 4d). Such types of stress risers are the primary zones for crack initiation and will ultimately result in premature fracture. It is, therefore, important to consider stress uniformity as an additional design requirement in the design of mechanical metamaterials. It should also be mentioned that the maximum von Mises stresses in soft and hard struts of these selected designs are lower than the tensile strengths of the individual materials in the bulk form.

Fig. 4: Stress distribution within the lattice structure.
figure 4

a The selection of a certain range of the elastic properties achieved for the unit cells with a cell angle of \(60^\circ\). In total, the elastic properties of 207 designs with various \({\rho }_{{\rm {h}}}\) values (i.e., 50%, 60%, 70% and 80%) fall within these selected ranges. b The maximum values of the von Mises stress in the structural elements of the corresponding lattice structures when these structures were subjected to two boundary conditions (i.e., \({\varepsilon }_{11}=3 \%\) or \({\varepsilon }_{22}=3 \%\)). Two designs were selected, including one with the minimum (node 1) and one (node 2) with the maximum Euclidean distance from the origin (b, c). The distribution of the von Mises stresses in the selected designs and their deformations under two boundary conditions (i.e., \(\,{\varepsilon }_{11}=3 \%\) or \({\varepsilon }_{22}=3 \%\)) are presented in (d). The axial stresses (S11) in the struts of each design under two boundary conditions (i.e., \(\,{\varepsilon }_{11}=3 \%\) or \({\varepsilon }_{22}=3 \%\)) are calculated and are compared with the axial stresses of the corresponding struts when the lattice structure is composed of an equivalent homogenous material (e).

Full size image

We also studied the distribution of the compressive or tensile axial stresses (S11) in individual struts of the selected designs under the aforementioned boundary conditions. That included \({S}_{11@{\varepsilon }_{22}=3 \% }\) vs. \({S}_{11@{\varepsilon }_{11}=3 \% }\) values as well as 95% confidence ellipses fitted to the stress values of individual struts for the multi-material designs (Fig. 4e). We then compared these results with the axial stresses obtained from a lattice structure with \({\rho }_{{\rm {h}}}=70 \%\) and equivalent homogenous material properties (Fig. 4e). This comparison highlighted that the lattice design with a lower stress riser point (i.e., design 1) was located inside the confidence ellipse of the design with the equivalent homogenous material (Fig. 4e). Such an approach can, therefore, be considered as additional design rule for selecting the optimum multi-material design with target properties.

Conclusions

In conclusion, deep learning models can accurately predict the mechanical properties of multi-materials mechanical metamaterials, reduce the speed of evaluating each design, and make parallel computing efficient and straightforward to the point where evaluating 1010−1020 designs is within reach. Our results show that such unprecedented sizes of the design database enable the rational design of multi-material mechanical metamaterials that not only achieve a very wide range of elastic properties but also meet additional design requirements. For example, we demonstrated that double-auxetic yet stiff designs can be realized using this approach. In this study, we examined two essential parameters in the design of multi-material mechanical metamaterials, namely the ratio of the volume of the hard phase to that of the soft phase (\({\rho }_{{\rm {h}}}\)) and the angle of the unit cells. In all simulations, the ratio of the elastic modulus of the hard phase to that of the soft phase was assumed to be constant and equal to 100. As increasing this ratio can increase the degree of non-affinity of the lattice structure38, it can have an influence on their overal mechanical properties. Therefore, this parameter can be further studied and considered as an input parameter for the training of the model to explore a broader range of mechanical properties. Another application demonstrated here is the addition of a criterion regarding stress uniformity that can reduce stress concentration in such types of mechanical metamaterials, thereby increasing their fracture and fatigue resistance.

Methods

We considered planar lattices with three groups of unit cell angles representing the negative (re-entrant, \({\theta }={60}{^\circ }\)), zero (orthogonal, \({\theta }={90}{^\circ }\)), and positive (honeycomb, \({\theta }={120}{^\circ }\)) values of the Poisson’s ratio (Fig. 1a). We kept the overall dimensions of each design (\({W}{,}{C}\)) as well as the dimensions of the constituent unit cells (\({w}{,}{c}\)) unchanged. All three groups of designs were composed of 5 × 5 unit cells with similar in-plane (\({t}\)) and out-of-plane (\({T}\)) thicknesses (Fig. 1a). The geometrical parameters of the designed lattice structures are presented in Supplementary Table 5. The hard and soft phases were randomly assigned to the struts of the structure so as to achieve various ratios of the volume of the hard phase to that of the soft phase (\({{\rho }}_{{{\rm {h}}}}\,\left({ \% }\right)={5},{10},{20},{30},{40},{50},{60},{70},{80},{90}{,}\) and \({95}\)). To further expand the space of possible mechanical properties, we studied the various combination of the unit cells. Moreover, we studied the stress distribution within the soft and hard elements of the unit cells and used a more uniform distribution of stresses as the criterion for selecting the best designs among all the designs with similar elastic properties.

Computational models

All FE models were created using MATLAB (MATLAB R2018b, Mathworks, USA) codes. The codes were used to design the three groups of lattice structures (composed of unit cells with the three different cell angles of \(60^\circ\), \(90^\circ\), and \(120^\circ\)), to randomly assign the hard and soft phases to the struts of each design, and to perform the FE simulations that estimate their mechanical properties (i.e., elastic modulus and Poisson’s ratio in two orthogonal directions). Our codes were further extended to combine single unit cell designs into four-tile and nine-tile lattice structures. In each structure, the adjacent designs were connected using a row of struts made of the hard material.

We used three-node quadratic beam elements (Timoshenko beam elements) with rectangular cross-sections and with two translational (i.e., \({u}_{x}\), \({u}_{y}\)) and one rotational (i.e., \({u}_{z}\)) degrees of freedom (DOF) at each node. We assigned elastic materials to both soft and hard phases with a similar Poisson’s ratio of 0.48 but vastly different Young’s moduli of 0.6 and 60 MPa (i.e., \(\frac{{E}_{{\rm {h}}}}{{E}_{{\rm {s}}}}=100\)), respectively. To estimate the mechanical properties of each structure in both the x- and y-directions, a strain of \(3 \%\) in each direction was separately applied to the structure. Towards this aim, in one model, the top nodes were subjected to a strain of \(3 \%\) in the y-direction (\({u}_{x}={u}_{z}=0\) and \({u}_{y}=3 \%\) strain), while all the degrees of freedom of the bottom nodes were constrained (\({u}_{x}={u}_{y}={u}_{z}=0\)). In the other model, the right nodes were subjected to \(3 \%\) strain in the x-direction (\({u}_{y}={u}_{z}=0,\) and ux = 3% strain), while all the degrees of freedom of the left nodes were constrained (\({u}_{x}={u}_{y}={u}_{z}=0\)). The element stiffness matrix transferred to the global coordinate (Ke) was calculated as42,43

$${K}^{{\rm {e}}}={Q}^{{\rm {T}}}{\bar{K}}^{{\rm {e}}}Q,$$
(1)
$${\bar{K}}^{{\rm {e}}}=\frac{E}{(1+\mu )}\left[\begin{array}{c}A(1+\mu )/L\\ 0\\ 0\\ -A(1+\mu )/L\\ 0\\ 0\end{array}\,\begin{array}{c}0\\ 12I/{L}^{3}\\ 6I/{L}^{2}\\ 0\\ -12I/{L}^{3}\\ 6I/{L}^{2}\end{array}\,\begin{array}{c}0\\ 6I/{L}^{2}\\ 4I(1+\mu /4)/L\\ 0\\ -6I/{L}^{2}\\ 2I(1-\mu /2)/L\end{array}\,\begin{array}{c}-A(1+\mu )/L\\ 0\\ 0\\ A(1+\mu )/L\\ 0\\ 0\end{array}\,\begin{array}{c}0\\ -12I/{L}^{3}\\ -6I/{L}^{2}\\ 0\\ 12I/{L}^{3}\\ -6I/{L}^{2}\end{array}\,\begin{array}{c}0\\ 6I/{L}^{2}\\ 2I(1-\mu /2)/L\\ 0\\ -6I/{L}^{2}\\ 4I(1+\mu /4)/L\end{array}\right],$$
(2)
$$\mu =\frac{12{EI}}{{L}^{2}{GA}{K}_{{\rm {s}}}},$$
(3)
$$Q=\left[\begin{array}{c}{n}_{x\bar{x}}\\ {n}_{x\bar{y}}\\ 0\\ 0\\ 0\\ 0\end{array}\,\begin{array}{c}{n}_{y\bar{x}}\\ {n}_{y\bar{y}}\\ 0\\ 0\\ 0\\ 0\end{array}\,\begin{array}{c}0\\ 0\\ 1\\ 0\\ 0\\ 0\end{array}\,\begin{array}{c}0\\ 0\\ 0\\ {n}_{x\bar{x}}\\ {n}_{x\bar{y}}\\ 0\end{array}\,\begin{array}{c}0\\ 0\\ 0\\ {n}_{y\bar{x}}\\ {n}_{{xy}}\\ 0\end{array}\,\begin{array}{c}0\\ 0\\ 0\\ 0\\ 0\\ 1\end{array}\right],$$
(4)

where \({\bar{K}}^{{\rm {e}}}\) is the local element stiffness matrix, and \(E,{A},{I},{{{{{\rm{and}}}}}}\,L\) are the elastic modulus, the cross-section area, the moment of inertia (\(I=T{t}^{3} / 12\)), and the length of the element, respectively. \(\mu\) is a dimensionless coefficient that characterizes the importance of shear-related parameters including \(G\) (shear modulus) and \({K}_{{\rm {s}}}\) (shear correction factor  = 0.85). \(Q\) is the transformation matrix and contains the direction cosines:

$${n}_{x\bar{x}}={n}_{y\bar{y}}=\frac{{x}_{2}-\,{x}_{1}}{L},\,{n}_{y\bar{x}}={-n}_{x\bar{y}}=\frac{{y}_{2}-\,{y}_{1}}{L}$$
(5)

where \({x}_{1},{y}_{1},{x}_{2},\) and \({y}_{2}\) are the element nodal coordinates.

The element load vector \({f}^{{\rm {e}}}\) is obtained as follows43:

$${f}^{{\rm {e}}}={Q}^{{\rm {T}}}{\bar{f}}_{{\rm {l}}}^{{\rm {e}}},$$
(6)
$${\bar{f}}_{{\rm {l}}}^{\rm {{e}}}=\left[\begin{array}{c}\begin{array}{c}\begin{array}{c}{q}_{\bar{x}}L/2\\ {q}_{\bar{y}}L/2\\ {q}_{\bar{y}}{L}^{2}/12\end{array}\\ {q}_{\bar{x}}L/2\\ {q}_{\bar{y}}L/2\end{array}\\ -{q}_{\bar{y}}{L}^{2}/12\end{array}\right]$$
(7)

The stiffness matrix and load vectors of all the elements were calculated and were assembled into a global stiffness matrix (\(K\)) and a global load vector (\(F\)). Finally, all the forces and displacements were calculated using Hook’s law (\(F={Kd}\)).

To calculate the Young’s moduli of the structure (\({E}_{11}=\frac{{\sigma }_{11}}{{\varepsilon }_{11}}\) and \({E}_{22}=\frac{{\sigma }_{22}}{{\varepsilon }_{22}}\)), the normal stresses in the directions 1 and 2 (\({\sigma }_{11}=\frac{\bar{{F}_{1}}}{{A}_{2}},{\sigma }_{22}=\frac{\bar{{F}_{2}}}{{A}_{1}}\), where \({A}_{1}\) and \({A}_{2}\) are the cross-section areas of the structure on the 1–3 and 2–3 planes (Fig. 1a)) were divided by the strain applied along the same direction (\({\varepsilon }_{11}={\varepsilon }_{22}=3 \%\)). In these equations, \({\bar{F}}_{1}\) and \({\bar{F}}_{2}\) are, respectively, the mean reaction forces along the directions 1 and 2 at the right and top nodes (\(\bar{{F}_{1}}=\frac{\mathop{\sum }\nolimits_{i=1}^{{n}_{{\rm {R}}}}{{F}_{1}}_{i}}{{n}_{{\rm {R}}}},\,\bar{{F}_{2}}=\frac{\mathop{\sum }\nolimits_{i=1}^{{n}_{{\rm {T}}}}{{F}_{2}}_{i}}{{n}_{{\rm {T}}}}\), where \({n}_{{\rm {R}}}\) and \({n}_{{\rm {T}}}\) are the total numbers of the right and top nodes while \({{F}_{1}}_{i}\) and \({{F}_{2}}_{i}\) are the reaction forces along the directions 1 and 2 at each of the right and top nodes, respectively). To calculate the Poisson’s ratio (\({\nu }_{12}={\nu }_{21}=-\frac{{\varepsilon }_{{{\rm {trans}}}}}{{\varepsilon }_{{{\rm {axial}}}}}\)), the transverse strain was first calculated as the ratio of the mean displacement of the lateral nodes to the initial transversal length of the structure. The transverse strain was then divided by the applied axial strain (in the case of \({{\varepsilon }_{{{\rm {axial}}}}=\varepsilon }_{11}=3 \% :\,{\varepsilon }_{{{\rm {trans}}}}={\varepsilon }_{22}=\,\frac{\mathop{\sum }\nolimits_{i=1}^{{n}_{{\rm {T}}}}\delta {y}_{i}}{{L}_{2}{n}_{{\rm {T}}}},\) and in the case of \({\varepsilon }_{{{\rm {axial}}}}={\varepsilon }_{22}=3 \% :\,{\varepsilon }_{{{\rm {trans}}}}={\varepsilon }_{11}=\) \(\frac{\mathop{\sum }\nolimits_{i=1}^{{n}_{{\rm {R}}}}\delta {x}_{i}}{{L}_{1}{n}_{{\rm {R}}}}\) where \({L}_{1}\) and \({L}_{2}\) are the initial lengths of the structure along the directions 1 and 2).

Deep learning

We implemented two artificial neural networks (ANN) using Tensorflow.keras neural network library44,45, namely the ‘single unit cell model’ and the ‘four-tile model’. The single unit cell model predicts the mechanical properties of the lattice structures with three unit cell angles of \(60^\circ\), \(90^\circ\), and \(120^\circ\) and a wide range of \({\rho }_{{\rm {h}}}\) values (i.e., \({\rho }_{{\rm {h}}}\,\left( \% \right)=5,10,20,30,40,50,60,70,80,90\), and \(95\)). To train the single unit cell model, the FE models were first solved for 18,150,000 lattice structures (16,500,000 structures as the training dataset and 1,650,000 structures as the testing dataset) with random assignments of the hard phase within the structure. The inputs to the single unit cell model included 150 material parameters indicating whether each strut was hard or soft (1 = hard, 0 = soft) and one unit cell angle (θ = 60°, 90°, and 120°) (151 inputs in total). The outputs of the model included the elastic moduli (E11, E22) and Poisson’s ratios (ν1, ν2) in both directions (4 outputs in total) (Fig. 1a). The dataset generated for the training of the single unit cell model was also used for the training of the four-tile deep learning model. Towards this aim, we selected 90 single unit cell tiles with mechanical properties uniformly distributed within the achievable range of elastic properties for these single unit cell designs. The mechanical properties of these 90 designs were first calculated by performing the FE simulations. All possible four-combinations of these single tiles (i.e., \(C\left(90,\,4\right)=2,555,190\)) considering the permutation of these four single tiles (=4!, which is reduced to 6 due to the symmetry of the structure) were generated and were used for setting up the deep learning models (\({n}_{2}=6\times 2,555,190=\,15,331,140\)). Our FE code was then used to calculate the overall elastic properties of these structures (Fig. 1b). We randomly selected 90% of the dataset as training dataset and the remaining 10% as testing dataset. The four-tile model was then created to map the space of the 16 input parameters (i.e., the elastic properties of the individual tiles) to the space of 4 output parameters (i.e., the elastic properties of the four-tile structures).

We scaled all the outputs of the single unit cell models and all the inputs and outputs of the four-tile model to the range [0–1] (see Table 1 for the scaling method). In post-processing, we scaled the relevant outputs back to the original range to facilitate the interpretation of the results.

For the training of both the single unit cell model and four-tile model, we used a sequential model composed of a linear stack of fully connected layers based on the Tensorflow.keras library. Before training the models, we configured the learning process by defining several parameters, including an optimizer (RMSprop), a list of metrics (MSE and MAE), and a loss function (MSE) that was the objective that the model would try to minimize. To evaluate the performance of the model with different hyperparameter values and also to detect overfitting during the training process, we assumed 20% of the training dataset as the validation dataset. This means that during each epoch, the model was trained based on the training data, and was tuned with the metrics (MSE, MAE) calculated for the validation dataset. In this way, we tuned the hyperparameters of the model based on the results of the metrics for the validation dataset.

In the single unit cell model, we systematically studied the effects of different hyperparameters (i.e., the number of hidden layers, the number of neurons in each hidden layer, learning rate, and activation function). To design the architecture of the four-tile model, we started with the optimized hyperparameters determined for the single unit cell model. Hyperparameter tuning is discussed in detail in the Supplementary Methods (Supplementary Figs. 4–7 and Supplementary Tables 6–10). The optimized architecture and hyperparameters of both models together with their optimized accuracy, the type of feature scaling, and the optimization algorithm are presented in Table 2.

Table 2 The training parameters of the single unit cell and four-tile deep learning models.
Full size table

In order to calculate the training error, the prediction results of the deep learning models were compared with the target values (FE simulation results) and MAE as well as MSE were calculated for each training epoch. MSE and MAE graphs for single unit cell model and four-tile model are presented in Supplementary Figs. 6 and 7, respectively. MAE quantifies the magnitude of the prediction error without considering the error direction:

$${{\rm {MAE}}}=\frac{1}{n}\mathop{\sum }\limits_{i=1}^{n}{{{{{{\rm{|}}}}}}y}_{i}-{\hat{y}}_{i}{{{{{\rm{|}}}}}}$$
(8)

where \(n\) is the number of the training samples, \({y}_{i}\) are the predicted values, and \({\hat{y}}_{i}\) are the true values. MSE is the squared mean of the differences between the predicated values, \({y}_{i}\), and the true values, \({\hat{y}}_{i}\), and is calculated as

$${{{{{{\rm{MSE}}}}}}}=\frac{1}{n}\mathop{\sum }\limits_{i=1}^{n}{\left({y}_{i}-{\hat{y}}_{i}\right)}^{2}$$
(9)

Experiments

To validate the results of our computational models used for training the single unit cell models, we selected three single unit cell lattice structures (one from each of the cell angles of \(60^\circ\), \(90^\circ\), and \(120^\circ\)) (Fig. 1a). In addition, we designed three nine-tile structures and four four-tile structures. These structures represented different arrangements of the single unit cell designs (see Fig. 3). The selected designs were 3D printed and mechanically tested.

We used a multi-material 3D printer (Object500 Connex3, Stratasys, US) which uses the jetting of multiple UV-curable polymers (Polyjet technology) for printing multi-material structures. The commercially available polymers VeroCyanTM (hard phase, RGD841) and Agilus30TM white (soft phase, FLX985) were employed (both from Stratasys, USA). The hard and soft phases were selected such that the ratio of the elastic modulus of the hard phase (\({E}_{{\rm {h}}}\cong\) 60  MPa) to that of the soft phase (\({E}_{{\rm {s}}}\cong\) 0.60 MPa) was around 100. We designed a pin and gripper system to attach the printed specimens to the mechanical testing machine. These parts were 3D printed using a fused deposition modeling (FDM) 3D printer (Ultimaker \({2}^{+}\), Geldermalsen, the Netherlands) from polylactic acid (PLA) filaments (MakerPoint PLA, 750 gr, Natural). A mechanical testing machine (LLOYD instrument LR5K, load cell = 100 N) was used to load the specimens under tension (stroke rate = 1 mm/min). The applied displacement and the reaction force were recorded to obtain the stress–strain curve by dividing the force by the initial cross-section area and dividing the displacement by the initial length of the specimen. The slope of the stress–strain curve represents the overall stiffness of the sample. This procedure was repeated for a total of 10 specimens. In addition, we used a digital camera to capture the lateral deformations of the specimens at the different steps of the applied longitudinal displacement. We used image analysis (a custom-made MATLAB code) to measure the transverse strain for all the lattice structures. The axial strain was directly measured from the crosshead displacement of the mechanical testing machine. We, then, defined the Poisson’s ratio as \(\nu =-\frac{{\varepsilon }_{{{\rm {trans}}}}}{{\varepsilon }_{{{\rm {axial}}}}}\) (the calculation of \({\varepsilon }_{{{\rm {trans}}}}\) and \({\varepsilon }_{{{\rm {axial}}}}\) was the same as computational models).

We also used the DIC technique to measure the full-field strain distribution during the uniaxial tensile tests for the selected single unit cell lattice structures. The surface of the specimens was first painted white. A spackle pattern was then applied to the surface using an airbrush. We used a DIC system (Q400-3D-12MP, LIMESS Messtechnik u. Software GmbH, Germany) equipped with two cameras (DCM 12.0 Mpixel, digital monochrome high performance GigE camera) to record a series of image pairs from two different angles that were later analyzed with the help of the associated commercial software (Istra4D, Germany) to establish the correlations in the images and calculate the full-field strain maps (Fig. 1a).